運(yùn)行參數(shù)對靜壓氣體軸承動力學(xué)特性的影響

李健，楊少柒，李曉明，李青

（1.航天低溫推進(jìn)劑技術(shù)國家重點(diǎn)實(shí)驗(yàn)室，北京 100190；2.華中科技大學(xué) 能源與動力工程學(xué)院，武漢 430074；3.中國科學(xué)院大學(xué)，北京 100049）

氣體軸承是以氣體為潤滑介質(zhì)的軸承，具有高速、清潔和高精度的優(yōu)點(diǎn)，廣泛應(yīng)用于低溫工程、精密工程、空間技術(shù)、醫(yī)療器械等工程領(lǐng)域。在低溫領(lǐng)域，尤其在大型低溫系統(tǒng)中，主要靠透平膨脹機(jī)的膨脹降溫，因此，其支承設(shè)備需要滿足較高的轉(zhuǎn)速及穩(wěn)定性要求；但由于氣體的黏度低，導(dǎo)致其剛度和阻尼小于其他形式的軸承，穩(wěn)定性較差［1］。

文獻(xiàn)［2］提出利用動剛度及動阻尼系數(shù)來描述軸承的動力學(xué)特征，此后，國內(nèi)外針對氣體軸承動力學(xué)參數(shù)的研究迎來新的篇章。計(jì)算軸承的特性系數(shù)就要求解可壓縮潤滑方程，通過提出一些簡化方法來求得其近似解析解，但其應(yīng)用條件及計(jì)算精度均有較多限制。隨著數(shù)值計(jì)算方法的發(fā)展，一些學(xué)者又通過數(shù)值計(jì)算的方法來求解動力學(xué)特性參數(shù)。文獻(xiàn)［3］首先把軸承和轉(zhuǎn)子結(jié)合為一個(gè)系統(tǒng)，研究了軸承-轉(zhuǎn)子系統(tǒng)的穩(wěn)定性問題，并提出了應(yīng)用8個(gè)線性化剛度以及阻尼系數(shù)的模型。文獻(xiàn)［4］將氣體軸承的動態(tài)壓力以及動態(tài)氣膜厚度通過多個(gè)小擾動量來表示，并關(guān)注擾動頻率對氣體軸承動力學(xué)參數(shù)的影響，但并沒有給出相關(guān)的計(jì)算結(jié)果。文獻(xiàn)［5-6］利用動載荷法，通過試驗(yàn)測量轉(zhuǎn)子的質(zhì)量動力學(xué)響應(yīng)，獲得系統(tǒng)的動態(tài)剛度以及阻尼系數(shù)。文獻(xiàn)［7］通過偏導(dǎo)數(shù)法求解了彈性箔片軸承的動力學(xué)特性問題。文獻(xiàn)［8-9］同樣采用偏導(dǎo)數(shù)法求解了動壓氣體軸承以及止推軸承的動力學(xué)特性，并且分析了擾動頻率以及承載載荷對動力學(xué)參數(shù)的影響。

文中采用偏導(dǎo)數(shù)法，主要針對靜壓氣體軸承的動力學(xué)參數(shù)進(jìn)行求解，分析靜壓氣體軸承運(yùn)行參數(shù)對軸承動力學(xué)參數(shù)及穩(wěn)定性的影響。

1 基本理論與計(jì)算方法

1.1 靜壓氣體軸承靜態(tài)潤滑方程

靜壓氣體軸承結(jié)構(gòu)如圖1所示。圖中，D為軸頸直徑；d為供氣孔直徑；B為軸承寬度；B1為供氣孔位置到軸承邊緣的距離；θ0為靜態(tài)時(shí)軸頸的偏位角；φ為量綱一的周向坐標(biāo)；φ＝0處為偏心方向。

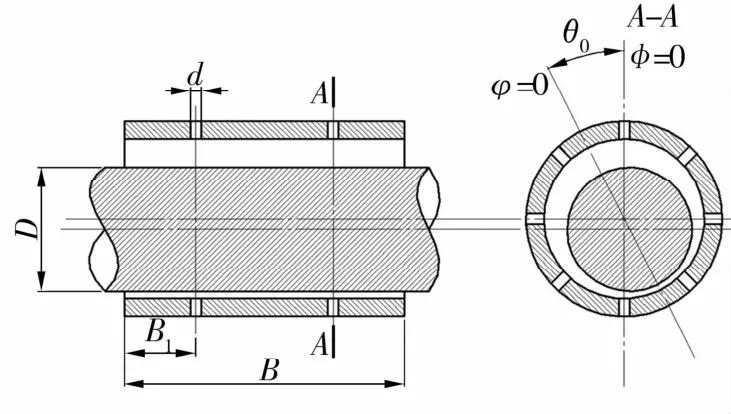
圖1 靜壓氣體軸承結(jié)構(gòu)示意圖Fig.1 Structure diagram of externally pressurized gas bearing

轉(zhuǎn)子懸浮依靠外部供氣（偏心率不為0）及轉(zhuǎn)子旋轉(zhuǎn)產(chǎn)生的動壓效應(yīng)來提供支承力。轉(zhuǎn)子間的氣膜間隙在微米量級，為軸承直徑的0.001倍，因此可以忽略氣體在氣膜厚度方向上的流動，僅考慮周向和軸向方向的流動，其誤差在允許范圍內(nèi)。由于氣體的黏性較小，在氣膜與轉(zhuǎn)子之間產(chǎn)生的摩擦熱很小，可以迅速通過熱傳導(dǎo)將熱量傳遞出去，因此，氣體的流動可以看成是等溫流動。綜上簡化，氣體潤滑方程量綱一的形式為［1］

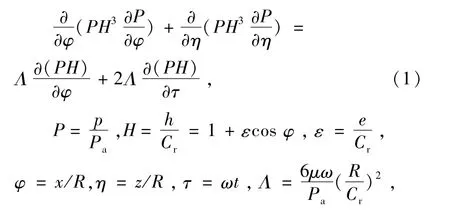
式中：P為量綱一的壓力；H為量綱一的氣膜厚度；Cr為氣膜半徑間隙；e為偏心率；p為壓力；Pa為環(huán)境大氣壓；ε為量綱一的偏心率；R為軸承半徑；η為量綱一的軸向坐標(biāo)；x，z分別為軸承周向、軸向坐標(biāo)；ω為轉(zhuǎn)子轉(zhuǎn)動角速度；τ為量綱一的時(shí)間；μ為氣體動力黏度；Λ為軸承數(shù)。

在供氣孔區(qū)域，通過小孔的質(zhì)量流量為［10］

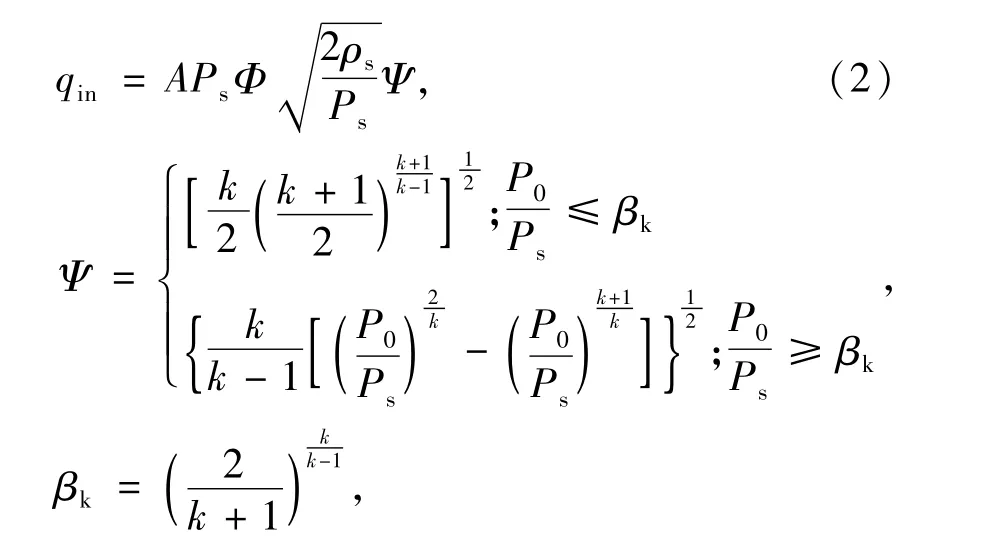
式中：A為供氣小孔的截面面積；Ps為供氣壓力；ρs為供氣壓力下的氣體密度；Φ 為流量系數(shù)，取0.8［10］；Ψ為速度系數(shù)；k為氣體絕熱指數(shù)；P0為節(jié)流孔出口壓力。

1.2 靜壓氣體軸承擾動狀態(tài)下的方程

當(dāng)轉(zhuǎn)子受到擾動時(shí)，轉(zhuǎn)子位置可以根據(jù)偏心角及偏位角來確定，將各參量的大小近似簡化為靜態(tài)量和擾動量的疊加，代入后可以得到擾動狀態(tài)下的潤滑方程［9-10］。

當(dāng)轉(zhuǎn)子繞平衡點(diǎn)以頻率ν進(jìn)行周期性擾動時(shí)，在任意時(shí)刻的擾動偏心率ε及偏位角θ分別記作E和Θ，因此，任一擾動時(shí)刻轉(zhuǎn)子的位置為［8-9］

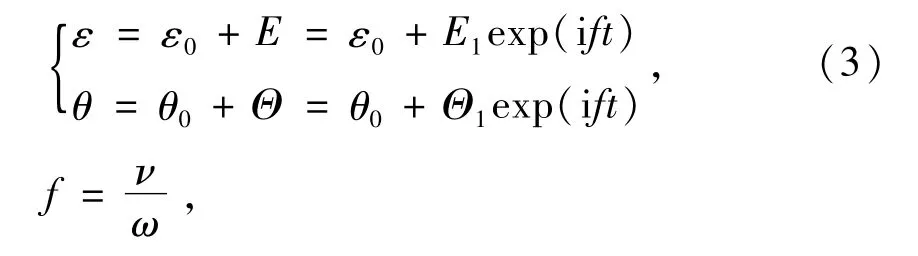
式中：E1為擾動偏心率幅值，復(fù)數(shù)；Θ1為擾動偏位角幅值，復(fù)數(shù)；f為量綱一的擾動頻率；ε0為靜態(tài)時(shí)的偏心率；i=。

根據(jù)線性法則進(jìn)行簡化，將擾動狀態(tài)下的氣膜厚度和壓力分別當(dāng)作靜態(tài)量H0，P0與動態(tài)量Hd，Pd的疊加，即

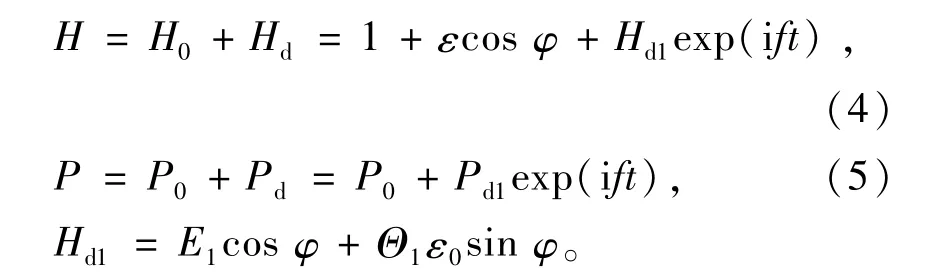
將（4），（5）式代入（1）式，利用穩(wěn)態(tài)方程化簡，忽略擾動的高階項(xiàng)，得到擾動狀態(tài)下的潤滑方程為［8-9］

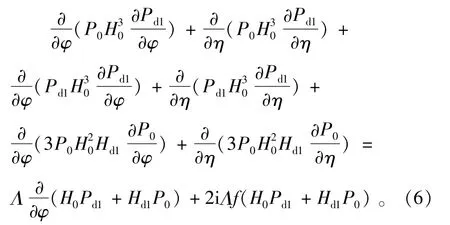
（6）式描述了擾動量幅值E1，Θ1與動態(tài)氣膜間隙厚度Hd1、動態(tài)壓力分布Pd1之間的聯(lián)系，是求解氣體軸承動態(tài)特性參數(shù)的基本方程。

1.3 動態(tài)剛度系數(shù)及阻尼系數(shù)的求解

擾動狀態(tài)下的潤滑方程隱含擾動幅值E1，Θ1，采用偏導(dǎo)數(shù)方法求解靜壓氣體軸承的動態(tài)特性參數(shù)。令

將擾動狀態(tài)的潤滑方程（6）式分別對E1，Θ1求導(dǎo)，得到關(guān)于PE，PΘ的偏微分方程。關(guān)于PE的偏微分方程為［8-9］

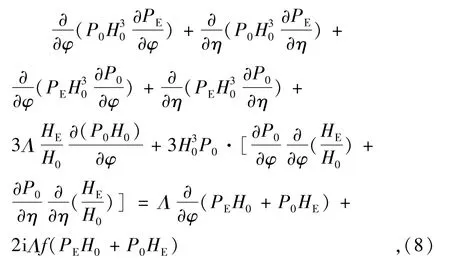
關(guān)于PΘ的偏微分方程為

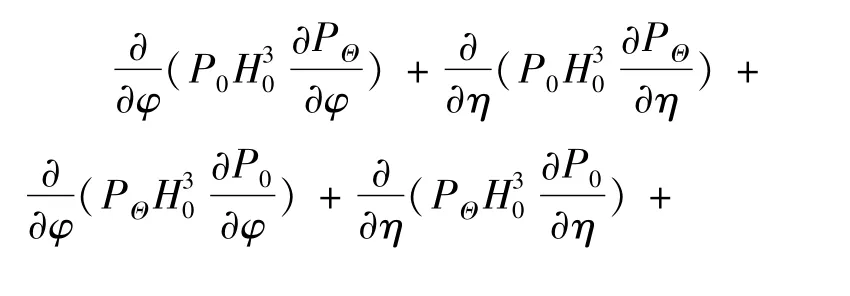
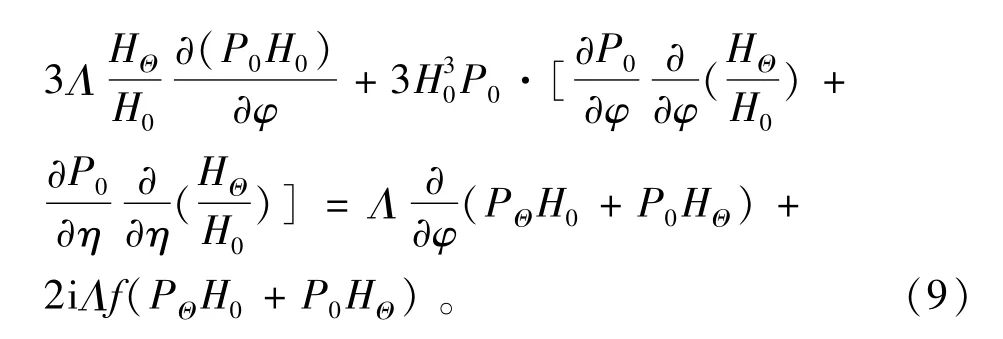
由于靜態(tài)氣膜厚度分布及靜態(tài)氣膜壓力分布為已知量，用有限差分法求解擾動狀態(tài)下的偏微分方程，軸承兩端的邊界條件為

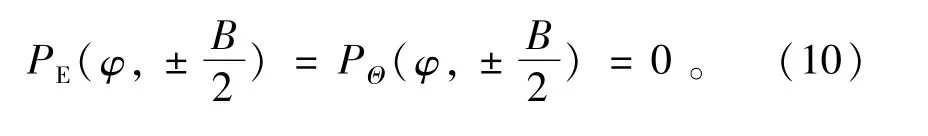
在供氣孔區(qū)域，由于轉(zhuǎn)子擾動直接影響供氣孔出口的壓力分布，其影響程度與此位置的壓力及氣膜厚度有關(guān)，因此，對于靜壓氣體軸承的動態(tài)特性參數(shù)的計(jì)算，供氣孔區(qū)域不作為邊界條件，而作為內(nèi)部計(jì)算的未知參數(shù)，這是與靜態(tài)計(jì)算壓力分布的區(qū)別所在。

求得PE和PΘ的分布后，靜壓氣體軸承量綱一的動態(tài)特性參數(shù)可以根據(jù)下列公式進(jìn)行計(jì)算［8-9］

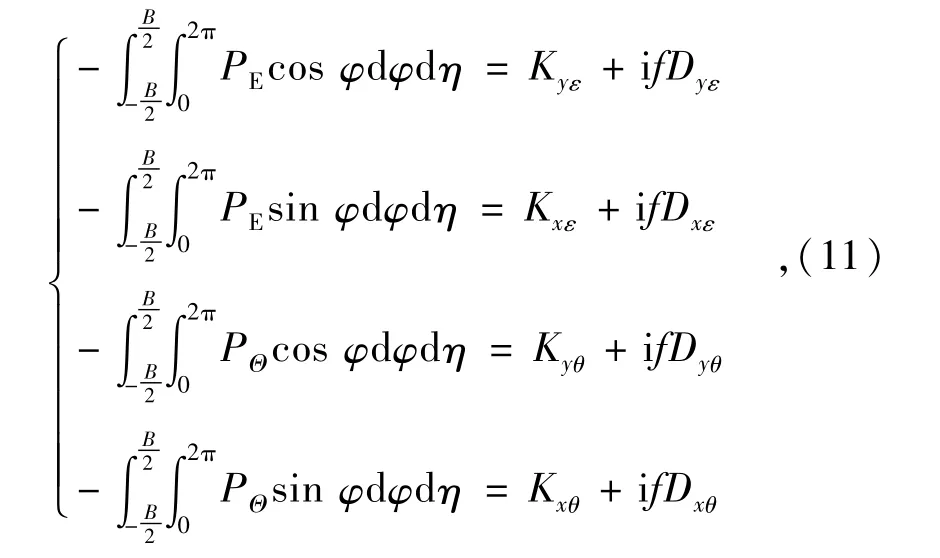
式中：Ki，j，Di，j分別為軸承的剛度和阻尼系數(shù)，其含義為j方向上的位移或速度變化引起在i方向力的變化量。

將（11）式得到的動力學(xué)特性參數(shù)轉(zhuǎn)化到直角坐標(biāo)系中［8-9］

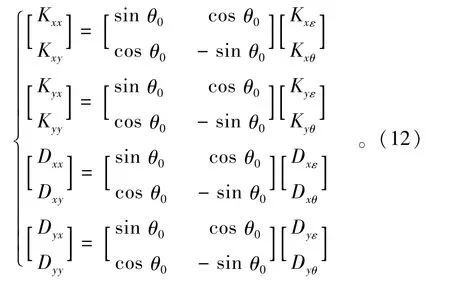
（12）式求得的結(jié)果就是靜壓氣體軸承在直角坐標(biāo)系下的動力學(xué)系數(shù)。

在求解擾動狀態(tài)的方程中，穩(wěn)態(tài)時(shí)的壓力分布及氣膜厚度分布均為已知量。供氣孔出口處的壓力大小與該處的氣膜厚度相關(guān)，假設(shè)擾動對于整個(gè)計(jì)算域有效，因此，擾動狀態(tài)下的供氣口出口參數(shù)不作為求解方程的邊界條件來設(shè)置，這是與求解靜態(tài)壓力分布方法的區(qū)別所在。

1.4 穩(wěn)定性分析理論方法

基于小擾動假設(shè)條件，轉(zhuǎn)子及軸承圍繞著靜態(tài)平衡點(diǎn)做小振幅振動，因此，軸承-轉(zhuǎn)子系統(tǒng)的運(yùn)動方程為［11］

式中：M 為系統(tǒng)質(zhì)量矩陣；K為剛度矩陣；C為阻尼矩陣；q為系統(tǒng)廣義坐標(biāo)序列。

將（13）式改寫為

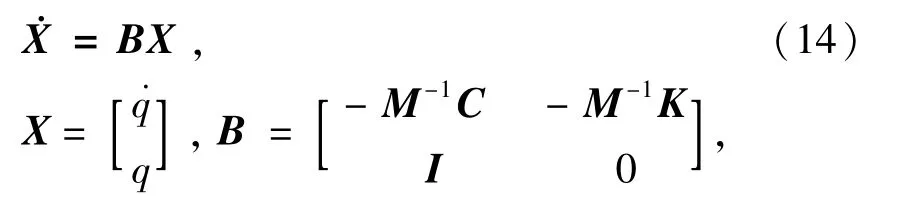
式中：X為狀態(tài)向量；B為狀態(tài)矩陣。

根據(jù)Routh-Hurwitz穩(wěn)定判別理論［12］，若矩陣B的特征值都有負(fù)的實(shí)部，則系統(tǒng)是穩(wěn)定的。因此，判定系統(tǒng)的穩(wěn)定性為判定矩陣B的特征值的正負(fù)性。

假設(shè)特征值的形式為λ1，2=-σ±iωd，基于小擾動的假設(shè)，系統(tǒng)的自由振動響應(yīng)為

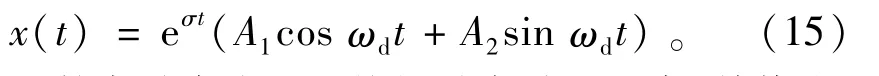
對數(shù)衰減率表征系統(tǒng)振動衰減的速率，其值為

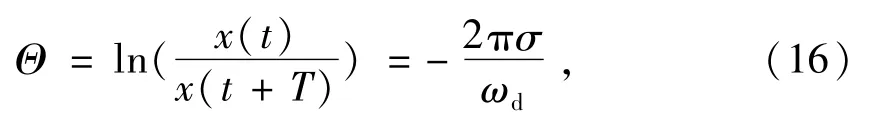
對于多自由度系統(tǒng)，其穩(wěn)定性采用最小的對數(shù)衰減率表示［12］

軸承與轉(zhuǎn)子之間的氣膜力可以近似用剛度和阻尼系數(shù)表示為

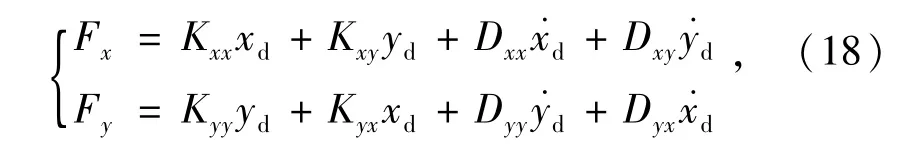
式中：Fx，F(xiàn)y分別為x，y方向上的氣膜力；xd，yd分別為轉(zhuǎn)子在x，y方向相對于平衡位置的位移變化量；˙xd，˙yd分別為轉(zhuǎn)子在x，y方向的速度。

軸承-轉(zhuǎn)子系統(tǒng)的運(yùn)動方程為

結(jié)合（18）和（19）式可以求得矩陣B，進(jìn)而分析系統(tǒng)的穩(wěn)定性。

2 動力學(xué)參數(shù)的計(jì)算結(jié)果及分析

計(jì)算所用的靜壓氣體軸承結(jié)構(gòu)尺寸及運(yùn)行參數(shù)見表1。根據(jù)上述理論，利用MATLAB軟件采用有限差法及偏導(dǎo)數(shù)法［9-10］編制程序計(jì)算軸承的動力學(xué)特性參數(shù)。對雙排孔供氣、每排8孔均布的靜壓氣體軸承進(jìn)行分析，重點(diǎn)研究供氣壓力、轉(zhuǎn)速及偏心率對軸承動力學(xué)特性參數(shù)的影響。

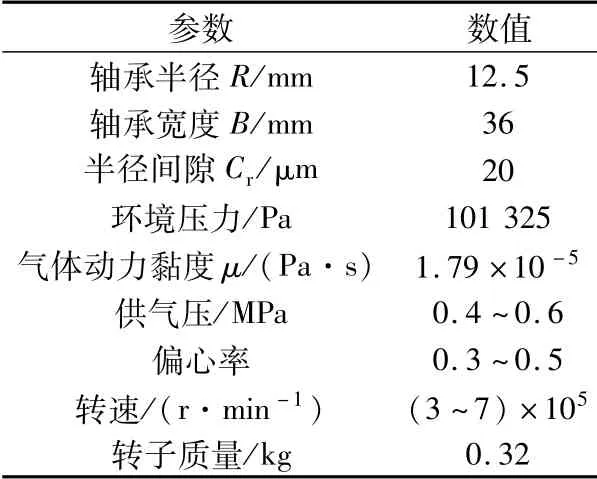
表1 軸承結(jié)構(gòu)尺寸及運(yùn)行參數(shù)Tab.1 Structural dimensions and operating parameters of bearing

通過有限差分法求解潤滑方程（1）式，并在供氣孔周圍滿足質(zhì)量守恒的條件下可以獲得靜壓氣體軸承的壓力分布。

2.1 擾動頻率的影響

供氣壓力4×105Pa、偏心率0.3、轉(zhuǎn)速5×105r/min下，靜壓氣體軸承氣膜間隙內(nèi)的壓力分布如圖2所示。

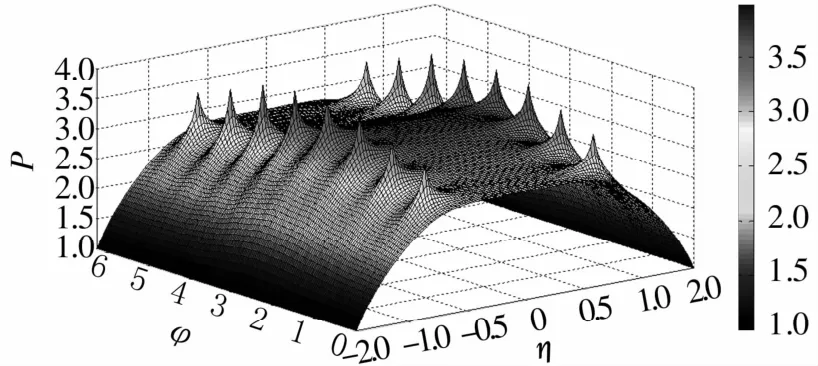
圖2 靜壓氣體軸承氣膜間隙壓力分布Fig.2 Pressure distribution in gas film clearance of externally pressurized gas bearing

在此運(yùn)行工況下軸承的動態(tài)剛度系數(shù)與動阻尼系數(shù)隨擾動頻率的變化情況如圖3所示。

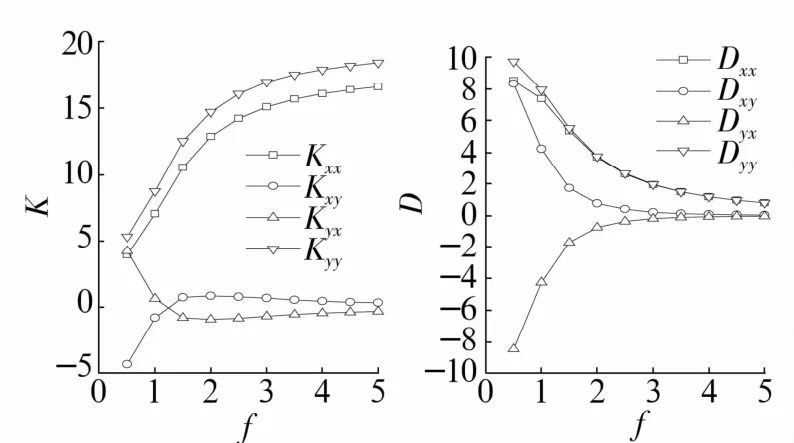
圖3 剛度系數(shù)與阻尼系數(shù)隨擾動頻率的變化Fig.3 Variation of stiffness and damping coefficients with disturbance frequency

由圖3可以看出：

1）靜壓氣體軸承的主剛度系數(shù)隨轉(zhuǎn)子擾動頻率的增加而增加，最終趨于一恒定值。交叉剛度的絕對值總體隨擾動頻率的增加而減小，最終趨于恒定值。

2）主阻尼系數(shù)隨轉(zhuǎn)子擾動頻率的增加而減少，最終趨于一恒定值，當(dāng)量綱一的擾動頻率大于1.5時(shí)，2個(gè)方向的主阻尼系數(shù)數(shù)值趨于一致；交叉阻尼系數(shù)的絕對值隨擾動頻率的增加而減小，最終趨于0，且關(guān)于y＝0對稱。

3）當(dāng)量綱一的擾動頻率大于1時(shí)，主剛度系數(shù)遠(yuǎn)大于交叉剛度系數(shù)；主阻尼系數(shù)也大于交叉阻尼系數(shù)。

2.2 供氣壓力的影響

在偏心率0.3、轉(zhuǎn)速3×105r/min下，不同供氣壓力對靜壓氣體軸承動力學(xué)特性系數(shù)的影響如圖4、圖5所示，并將計(jì)算結(jié)果與相同尺寸下的動壓氣體軸承作比較。

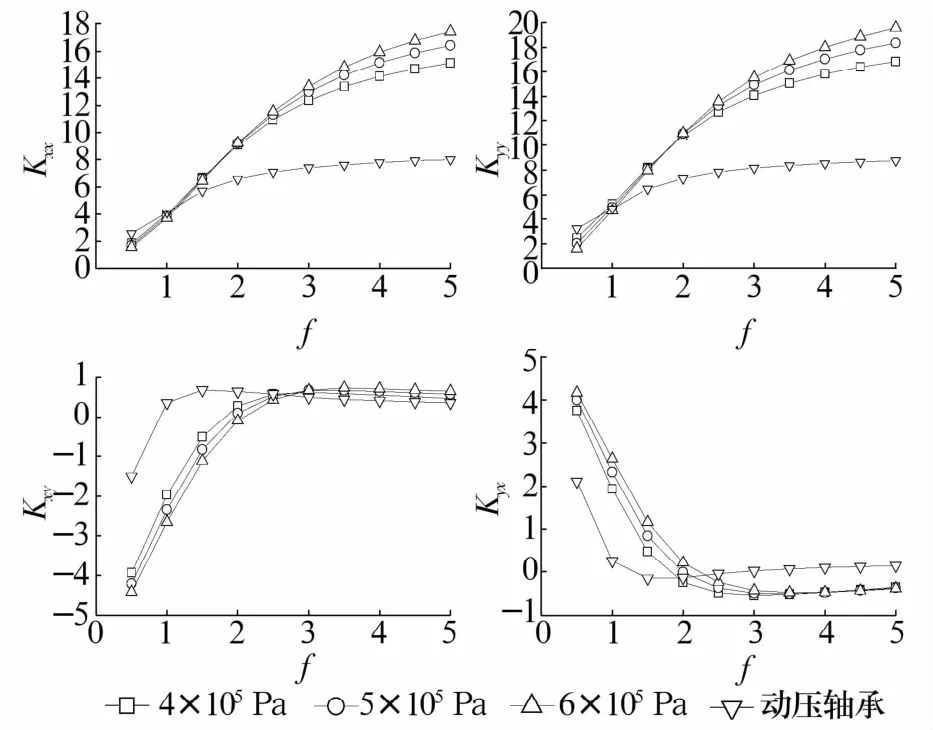
圖4 剛度系數(shù)隨供氣壓力的變化Fig.4 Variation of stiffness coefficients with gas supply pressure

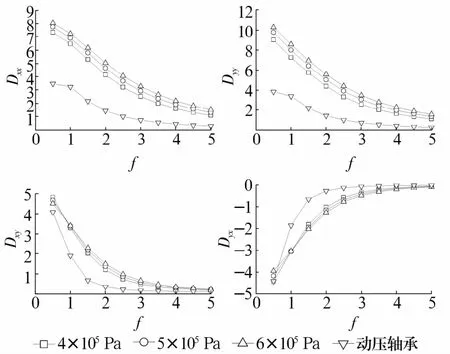
圖5 阻尼系數(shù)隨供氣壓力的變化Fig.5 Variation of damping coefficients with gas supply pressure

由圖4、圖5可以看出：

1）當(dāng)量綱一的擾動頻率小于2.5時(shí)，供氣壓力對主剛度系數(shù)的影響不大；當(dāng)量綱一的擾動頻率大于2.5時(shí)，主剛度系數(shù)隨供氣壓力的增加而增加，差值呈逐漸增大趨勢，最終趨于穩(wěn)定；主阻尼系數(shù)隨壓力的增加而增加。

2）交叉剛度系數(shù)與供氣壓力的關(guān)系并不明顯，不同壓力下的交叉剛度數(shù)值相差不大，當(dāng)量綱一的擾動頻率小于3時(shí)，Kxy與供氣壓力成反比，Kyx與供氣壓力成正比；當(dāng)量綱一的擾動頻率大于3時(shí)，交叉剛度幾乎與供氣壓力無關(guān)；

3）當(dāng)量綱一的擾動頻率小于1時(shí)，動壓氣體軸承的主剛度系數(shù)略大于靜壓氣體軸承；當(dāng)量綱一的擾動頻率大于1時(shí)，靜壓氣體軸承的主剛度系數(shù)增加幅度遠(yuǎn)大于動壓氣體軸承；靜壓氣體的主阻尼系數(shù)大于動壓氣體軸承，并隨著擾動頻率的增加呈減小趨勢。

4）當(dāng)量綱一的擾動頻率小于2.5，動壓氣體軸承交叉剛度項(xiàng)Kxy大于靜壓氣體軸承，當(dāng)量綱一的擾動頻率繼續(xù)增加，其值略小于靜壓氣體軸承；當(dāng)量綱一的擾動頻率小于2時(shí)，交叉剛度項(xiàng)Kyx小于靜壓氣體軸承；當(dāng)量綱一的擾動頻率大于2，由于靜壓氣體軸承的此項(xiàng)有減小趨勢，導(dǎo)致最終動壓氣體軸承大于靜壓氣體軸承。動壓氣體軸承的阻尼交叉項(xiàng)Dxy整體小于靜壓氣體軸承，動壓氣體軸承的Dyx大于靜壓氣體軸承。

2.3 旋轉(zhuǎn)速度的影響

在供氣壓力4×105Pa、偏心率0.3下，靜壓氣體軸承的轉(zhuǎn)速對動剛度系數(shù)和動阻尼系數(shù)的影響分別如圖6、圖7所示。

由圖6、圖7可以看出：

圖6 剛度系數(shù)隨轉(zhuǎn)速的變化Fig.6 Variation of stiffness coefficients with rotating speed

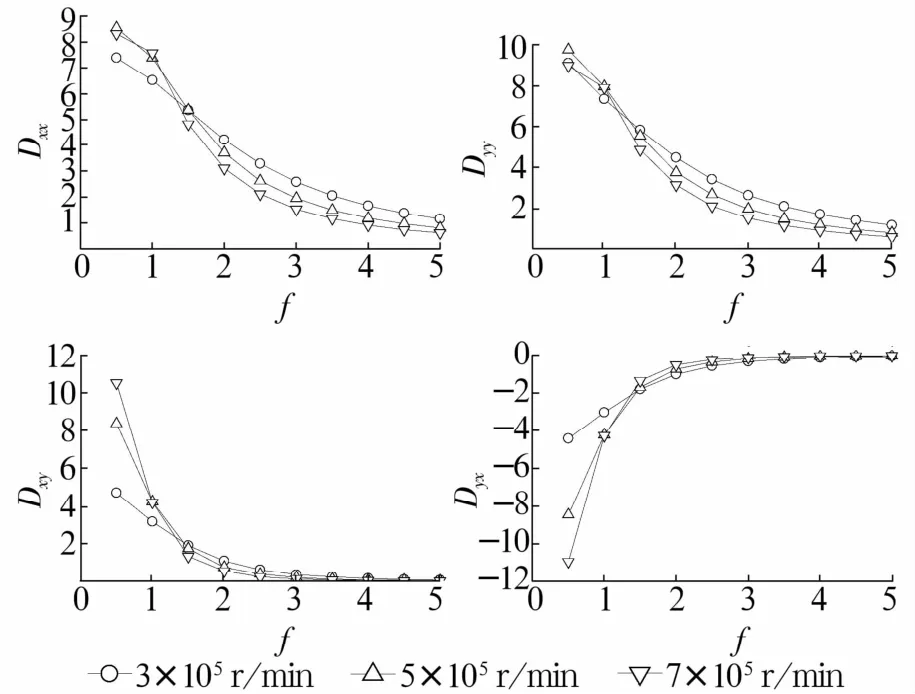
圖7 阻尼系數(shù)隨轉(zhuǎn)速的變化Fig.7 Variation of damping coefficients with rotating speed

1）靜壓氣體軸承主剛度系數(shù)隨著轉(zhuǎn)速的增加而增加；當(dāng)量綱一的擾動頻率大于1.5時(shí)，主阻尼系數(shù)隨轉(zhuǎn)速的增加而減小。

2）當(dāng)量綱一的擾動頻率小于2.5時(shí)，交叉剛度系數(shù)Kxy總體上隨轉(zhuǎn)速的增加而增加，Kyx隨轉(zhuǎn)速的增加而減少；當(dāng)量綱一的擾動頻率大于2.5時(shí)，轉(zhuǎn)速對交叉剛度的影響不大。當(dāng)量綱一的擾動頻率小于1.5時(shí)，交叉阻尼系數(shù)Dxy隨轉(zhuǎn)速的增加而增加，Dyx隨轉(zhuǎn)速的增加而減小；當(dāng)量綱一的擾動頻率大于1.5時(shí)，轉(zhuǎn)速對交叉阻尼的影響不大。

2.4 偏心率的影響

在供氣壓力5×105Pa、轉(zhuǎn)速3×105r/min下，靜壓氣體軸承的偏心率對動剛度系數(shù)和動阻尼系數(shù)的影響分別如圖8、圖9所示。

由圖8、圖9可以看出：

圖8 剛度系數(shù)隨偏心率的變化Fig.8 Variation of stiffness coefficients with eccentricity

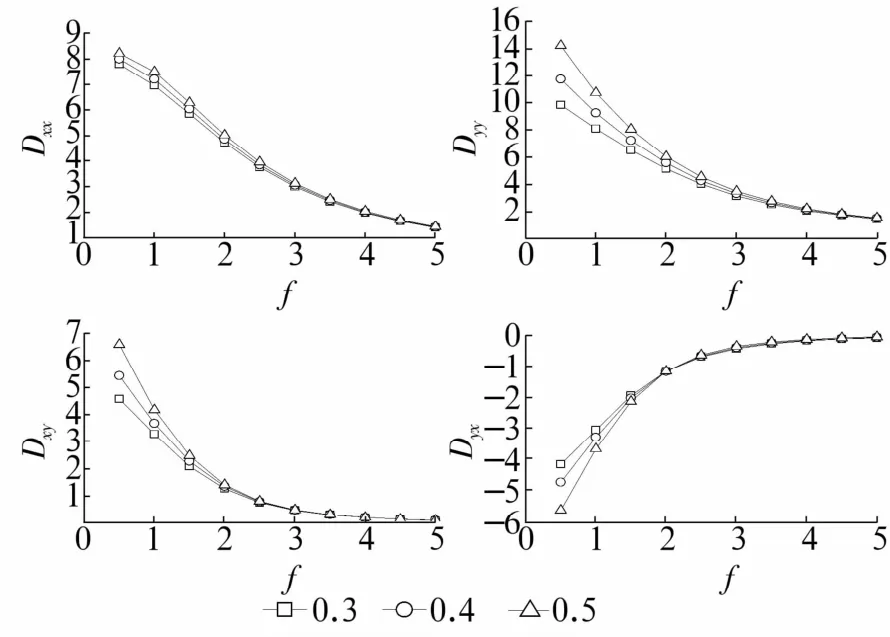
圖9 阻尼系數(shù)隨偏心率的變化Fig.9 Variation of damping coefficients with eccentricity

1）主剛度系數(shù)隨偏心率的增加而增加，且在承載方向的影響要遠(yuǎn)大于非承載方向；主阻尼系數(shù)也隨偏心率的增加而增加，當(dāng)量綱一的擾動頻率大于2.5時(shí)，偏心率對阻尼系數(shù)的影響大大減少。

2）當(dāng)量綱一的擾動頻率小于1時(shí)，交叉剛度系數(shù)Kxy隨偏心率而減小，Kyx隨偏心率的增加而增大；當(dāng)量綱一的擾動頻率大于1時(shí)，Kxy隨偏心率的增加而增加，Kyx隨偏心率的增加而減小。當(dāng)量綱一的擾動頻率小于2時(shí)，交叉阻尼系數(shù)Dxy隨偏心率的增加而增加，Dyx隨偏心率的增加而減小；當(dāng)量綱一的擾動頻率大于2時(shí)，偏心率對交叉阻尼系數(shù)的影響不大。

3 穩(wěn)定性分析

穩(wěn)定性分析基于小振動假設(shè)的條件，由于系統(tǒng)對擾動的抵抗力可以用振動衰減速率表示，因此用對數(shù)衰減率來衡量系統(tǒng)的穩(wěn)定性，對數(shù)衰減率越大，系統(tǒng)穩(wěn)定性越好。

在轉(zhuǎn)速3×105r/min、偏心率0.3下，靜壓氣體軸承的穩(wěn)定性如圖10所示，并與相同結(jié)構(gòu)尺寸下的動壓軸承作對比。

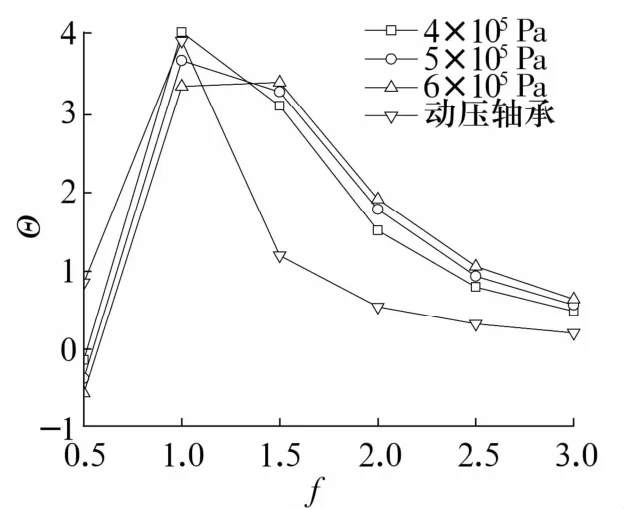
圖10 穩(wěn)定性隨供氣壓力的變化Fig.10 Variation of stability with gas supply pressure

由圖10可以看出：

1）動壓軸承在1倍頻以下的擾動時(shí)的穩(wěn)定性優(yōu)于靜壓氣體軸承；量綱一的擾動頻率大于1時(shí)，靜壓氣體軸承具有更好的穩(wěn)定性。

2）當(dāng)量綱一的擾動頻率低于1時(shí)，低供氣壓力顯示出更好的穩(wěn)定性能，當(dāng)量綱一的擾動頻率大于1.5時(shí)，高供氣壓力下的軸承具有更好的穩(wěn)定性能。

3）低頻擾動相對于高頻擾動更容易使氣體軸承發(fā)生失穩(wěn)。

靜壓氣體軸承的穩(wěn)定性隨工作轉(zhuǎn)速及偏心率的變化關(guān)系分別如圖11、圖12所示。

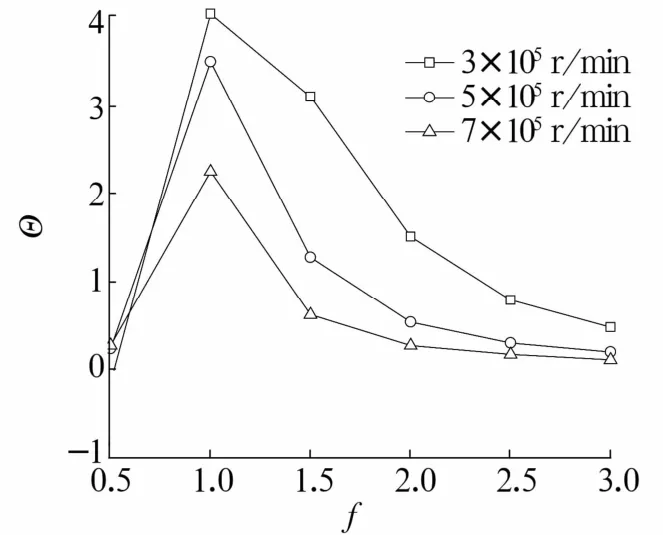
圖11 穩(wěn)定性隨轉(zhuǎn)速的變化Fig.11 Variation of stability with rotating speed

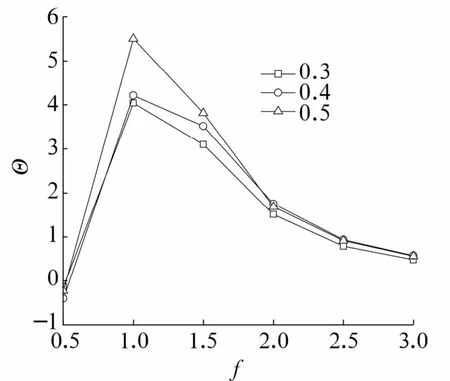
圖12 穩(wěn)定性隨偏心率的變化Fig.12 Variation of stability with eccentricity

由圖11、圖12可以看出：

1）靜壓氣體軸承的穩(wěn)定性與旋轉(zhuǎn)速度成反比，且高頻擾動下更容易失穩(wěn)。

2）大偏心率下的穩(wěn)定性更好，因此適當(dāng)提高靜壓氣體軸承的偏心可以提高運(yùn)轉(zhuǎn)穩(wěn)定性。

4 結(jié)論

利用MATLAB編程，應(yīng)用偏導(dǎo)數(shù)法求解了靜壓氣體軸承的動剛度系數(shù)以及動阻尼系數(shù)，分析了供氣壓力、轉(zhuǎn)速以及偏心率對動力學(xué)參數(shù)的影響，結(jié)果表明：

1）靜壓氣體軸承的主剛度系數(shù)及主阻尼系數(shù)隨供氣壓力的增加而增大，剛度與阻尼的交叉項(xiàng)隨著壓力的變化相對復(fù)雜。

2）當(dāng)量綱一的擾動頻率小于1時(shí)，動壓氣體軸承的主剛度略大于靜壓氣體軸承；當(dāng)量綱一的擾動頻率大于1時(shí)，靜壓氣體軸承的主剛度遠(yuǎn)大于動壓氣體軸承；靜壓氣體軸承的主阻尼系數(shù)遠(yuǎn)大于動壓氣體軸承。

3）主剛度系數(shù)隨轉(zhuǎn)速的增加而增加，當(dāng)量綱一的擾動頻率大于1.5時(shí)，主阻尼系數(shù)隨轉(zhuǎn)速的增加而減小；交叉剛度系數(shù)及交叉阻尼系數(shù)影響相對較小且規(guī)律復(fù)雜。

4）主剛度系數(shù)及主阻尼系數(shù)隨偏心率的增加而增大，且承載方向上的主剛度系數(shù)及主阻尼系數(shù)對偏心率更為敏感；交叉剛度系數(shù)隨偏心率的變化規(guī)律復(fù)雜，交叉阻尼系數(shù)的絕對值隨偏心率的增加而增加，且隨擾動頻率的增加，交叉阻尼項(xiàng)隨偏心率的變化較小。

5）量綱一的擾動頻率為1時(shí)的靜壓氣體或動壓氣體軸承的穩(wěn)定性最高，且低頻的擾動相比于高頻擾動更容易產(chǎn)生運(yùn)轉(zhuǎn)不穩(wěn)定。

6）適當(dāng)增加靜壓氣體軸承的偏心率會增加其運(yùn)轉(zhuǎn)穩(wěn)定性。