平面彈性五桿機構(gòu)的振動與構(gòu)件彈性振動的平衡優(yōu)化

江長云, 孫志宏, RAHMAN Habibur, 蔡聞然, 高明揚, 王 歡, 劉 智

(東華大學(xué) 機械工程學(xué)院, 上海 201620)

平面彈性五桿機構(gòu)的振動與構(gòu)件彈性振動的平衡優(yōu)化

江長云, 孫志宏, RAHMAN Habibur, 蔡聞然, 高明揚, 王 歡, 劉 智

(東華大學(xué) 機械工程學(xué)院, 上海 201620)

采用SPACAR軟件建立平面彈性五桿機構(gòu)的有限元模型, 在Matlab環(huán)境下對其進行動力學(xué)仿真分析. 仿真結(jié)果表明, 通過不斷增大曲柄轉(zhuǎn)速, 機構(gòu)的振動和構(gòu)件的彈性振動均不斷加劇. 將機構(gòu)的振動、構(gòu)件的彈性振動以及二者的綜合作為3種不同的優(yōu)化目標(biāo), 利用部分冗余伺服電機(PRSM)法對SPACAR建立的有限元模型進行平衡優(yōu)化, 探討3種優(yōu)化目標(biāo)的優(yōu)化效果. 結(jié)果表明: 以構(gòu)件的振動為目標(biāo)函數(shù)雖然可以改善桿件的彈性振動, 但是會使機構(gòu)的整體振動加劇；以機構(gòu)振動力矩為目標(biāo)函數(shù)或者以構(gòu)件的振動和機構(gòu)的振動二者的綜合為目標(biāo)函數(shù)均可同時平衡機構(gòu)的振動和構(gòu)件的彈性振動, 但前者對機構(gòu)振動的平衡效果更好.

五桿機構(gòu)；彈性；平衡；動力學(xué)；部分冗余伺服電機法

機構(gòu)在運動過程中, 其總質(zhì)心位置隨機構(gòu)運動而變化, 所產(chǎn)生的慣性力通過固定鉸鏈點傳遞給機架引起機構(gòu)的整體振動(shaking), 一般用振動力、振動力矩表示. 現(xiàn)代機械的發(fā)展趨勢是高速化和輕型化, 高速化會大幅增加機構(gòu)的慣性力, 而輕型化使構(gòu)件在高速運動過程中更容易產(chǎn)生彈性振動(vibration). 對于彈性機構(gòu), 機構(gòu)的慣性力使機構(gòu)產(chǎn)生振動力和振動力矩, 而振動力和振動力矩又導(dǎo)致構(gòu)件的振動、變形, 構(gòu)件變形必定會改變慣性力, 從而增加振動力和振動力矩, 因此, 慣性力傳遞到機架而形成的機構(gòu)整體振動與構(gòu)件的彈性振動是兩個耦合的動力學(xué)指標(biāo)[7]. 機構(gòu)整體振動與構(gòu)件彈性振動均會惡化機構(gòu)的工作性能, 影響執(zhí)行端軌跡的精度, 所以對彈性機構(gòu)進行平衡時, 有必要同時考慮這兩個動力學(xué)指標(biāo).

對平面彈性機構(gòu)動力學(xué)研究的文獻已有很多, 但研究內(nèi)容主要集中在機構(gòu)振動的平衡[1]或構(gòu)件彈性振動的抑制[2]這兩個方面. 文獻[3-4]通過控制附加的冗余驅(qū)動器在振動力、振動力矩的最大值附近施加的冗余驅(qū)動力矩，使機構(gòu)的振動得到了較好的平衡. 文獻[5-7]利用部分冗余伺服電機法(PRSM法)對彈性機構(gòu)的振動進行動平衡優(yōu)化并取得了良好的平衡效果. 與冗余驅(qū)動法相比, PRSM法不需要添加額外的元件, 具有一定的優(yōu)越性[5]. 其中, 文獻[6]利用PRSM法調(diào)節(jié)平面彈性五桿機構(gòu)兩曲柄的轉(zhuǎn)速來減小機構(gòu)的振動, 但是并沒有研究對構(gòu)件彈性振動的優(yōu)化效果.

本文在文獻[6]研究工作的基礎(chǔ)上, 以平面彈性五桿機構(gòu)為研究對象, 忽略負(fù)載和間隙的影響, 利用彈性動力學(xué)仿真軟件建立該機構(gòu)的有限元模型, 利用PRSM法對該機構(gòu)的振動和構(gòu)件的彈性振動進行動力學(xué)平衡優(yōu)化, 探討不同優(yōu)化指標(biāo)對彈性五桿機構(gòu)動平衡優(yōu)化效果的影響.

1 有限元理論分析

1.1 機構(gòu)振動分析

彈性五桿機構(gòu)有限元模型[8]如圖1所示, 由曲柄(1)、連桿(2)、連桿(3)、曲柄(4)和機架組成. 兩曲柄各劃分為一個梁單元, 兩連桿各劃分為兩個梁單元, 故整個系統(tǒng)由6個梁單元組成.Ui(i=1～22)表示廣義坐標(biāo), (1)～(4)表示桿件編號, 1～7表示節(jié)點編號, ①～⑥表示梁單元編號.

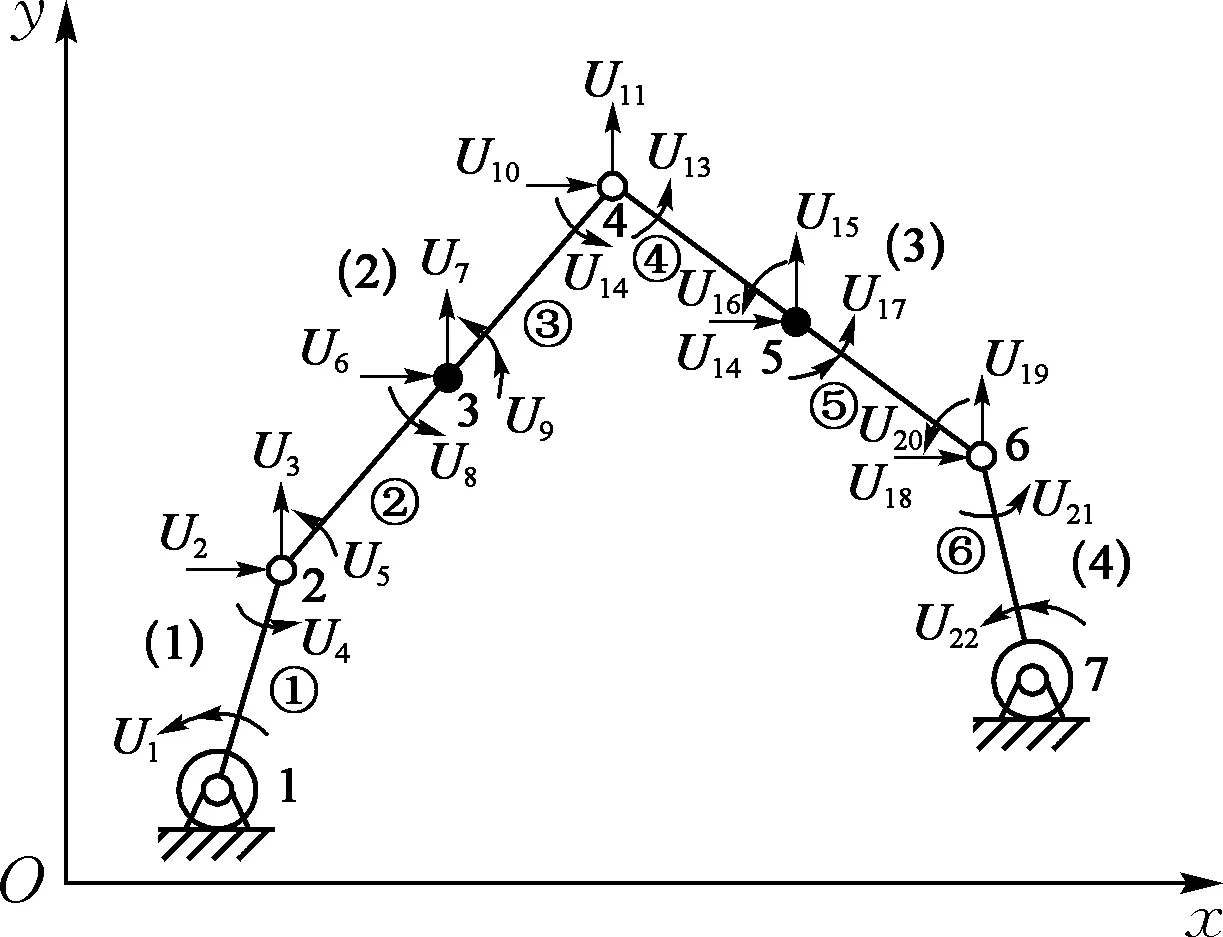
圖1 彈性五桿機構(gòu)有限元模型Fig.1 The finite model of elastic five-bar mechanism

梁單元的運動微分方程為

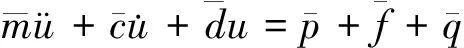
(1)

現(xiàn)將各單元的運動微分方程組裝起來, 整個系統(tǒng)的運動微分方程為

(2)

機構(gòu)的振動力和振動力矩實際上是機構(gòu)對機架所施加的力和力矩. 機架的受力示意圖如圖2所示. 機構(gòu)所受的4個力, 分別與副反力F1x、F1y、F7x、F7y大小相等, 方向相反.

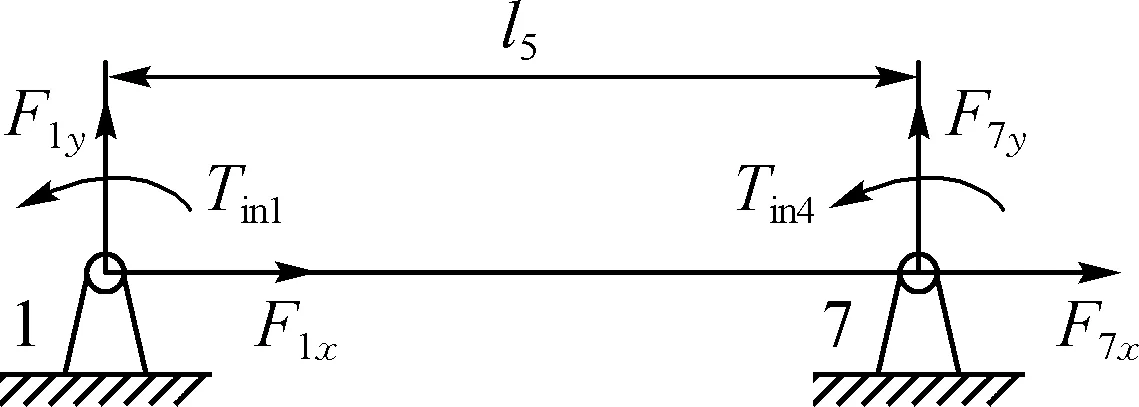
圖2 機架受力分析Fig.2 The force analysis of rack

Tin1、Tin4為電機的輸入力矩, 可求得機構(gòu)的振動力Fsh和振動力矩Msh[4]為

(3)

(4)

式中:l5為節(jié)點1到7的距離.

1.2 構(gòu)件彈性振動分析

由于將構(gòu)件劃分為梁單元, 因此，構(gòu)件的彈性振動分析可以簡化成梁單元的振動分析. 需特別申明, 本文中梁單元的振動是指橫向振動(忽略梁的縱向振動), 梁單元的振動幅度用梁的軸線橫向位移來描寫. 平面彈性梁單元[9]如圖3所示, 節(jié)點p、q的位置向量分別為(xp,yp)、(xq,yq), 角度φp、φq分別代表了Rpnx、Rqnx與x軸的夾角.Rpnx與Rpny為過節(jié)點p的相互垂直的向量, 而Rqnx和Rqny過節(jié)點q的相互垂直的向量. 當(dāng)梁單元未變形時,Rpnx和Rqnx沿著梁軸線,Rpny和Rqny垂直于梁的軸線. 其中, 平面旋轉(zhuǎn)矩陣Rp和Rq具體為

(5)

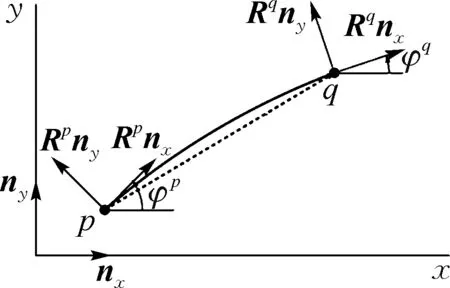
圖3 平面彈性梁單元Fig.3 Planar flexible beam element

梁單元k的節(jié)點坐標(biāo)可以表示為

(6)

平面梁單元的彎曲變形示意圖如圖4所示.

圖4 平面彈性梁單元的彎曲變形Fig.4 Bending deformations of the planar beam element

(7)

式中:ny=[0, 1]T,l(k)=[(xq-xp), (yq-yp)]T.

在如圖1所示的彈性五桿機構(gòu)有限元模型中, 兩連桿分別劃分為兩個梁單元, 連桿2由梁單元②和梁單元③組成, 連桿3由梁單元④和梁單元⑤組成, 所以, 連桿2和連桿3中點彎曲變形V2和V3[11]可以分別表示為

(8)

2 彈性五桿機構(gòu)動力學(xué)仿真研究

以文獻[6]中平面彈性五桿機構(gòu)作為實例, 曲柄(1)桿長為80 mm, 截面寬為3.3 mm, 高為1.1 mm； 連桿(2)桿長為250 mm, 截面寬為2.9 mm, 高為1.8 mm；連桿(3)幾何參數(shù)與連桿(2)一致；曲柄(4)桿長為100 mm, 截面寬為4.2 mm, 高為1.4 mm；機架長為250 mm. 轉(zhuǎn)動副B的集中質(zhì)量為0.012 4 kg, 轉(zhuǎn)動慣量為1.116×10-7kg·m2；轉(zhuǎn)動副C的集中質(zhì)量為0.014 6 kg, 轉(zhuǎn)動慣量為1.314×10-7kg·m2；轉(zhuǎn)動副D的集中質(zhì)量為0.013 3 kg, 轉(zhuǎn)動慣量為1.197×10-7kg·m2. 構(gòu)件材料: 鋼, 密度ρ=7 800 kg/m3, 彈性模量E=2×1011Pa, 剪切模量G=8×1010Pa.

由于彈性五桿機構(gòu)的動力學(xué)模型是非線性、強耦合的時變微分方程, 求解過程比較麻煩. 因此, 本文利用SPACAR軟件直接建立平面彈性五桿機構(gòu)有限元模型. SPACAR軟件是一款基于非線性有限元理論的多自由度機構(gòu)的動力學(xué)仿真軟件[10-11]，它需要在Matlab軟件環(huán)境下運行使用, 這也為SPACAR軟件與Matlab優(yōu)化工具箱的結(jié)合提供了可能.

令兩曲柄的轉(zhuǎn)速ω1和ω4相等, 且初始角度均為0°， 改變兩曲柄轉(zhuǎn)速, 使之從0增至250 r/min, 得到彈性五桿機構(gòu)的振動力和振動力矩的最大幅值的變化曲線如圖5所示, 連桿(2)和連桿(3)中點彎曲變形的最大幅值的變化曲線如圖6所示.

圖5 振動力和振動力矩變化曲線Fig.5 The change of shaking force and shaking moment

圖6 連桿中點彎曲變形變化曲線Fig.6 The change of bending deformation

從圖5可以看出, 隨著轉(zhuǎn)速的增大, 機構(gòu)的振動力和振動力矩也在不斷增大, 說明曲柄轉(zhuǎn)速增大, 機構(gòu)整體振動加劇. 從圖6可以看出, 曲柄轉(zhuǎn)速增大, 構(gòu)件中點的彎曲變形增加, 且隨著轉(zhuǎn)速的增長,彎曲變形增長的速率也增大. 因此, 機構(gòu)運動過程中, 彈性連桿存在振動, 且隨著曲柄轉(zhuǎn)速的增加, 機構(gòu)整體振動和連桿彈性振動的程度均加劇.

優(yōu)化目標(biāo)函數(shù)為

(9)

(10)

(11)

式中:W1、W2、W3、W4、W5、W6為加權(quán)系數(shù), 其值分別取為W1=W2=0.5,W3=W4=W5=W6=0.25.

以上述3種目標(biāo)函數(shù)為優(yōu)化目標(biāo), 通過Matlab優(yōu)化工具箱里的遺傳算法(GA)進行優(yōu)化, 得到如表1所示的優(yōu)化效果.

表1 3種目標(biāo)函數(shù)的優(yōu)化效果

注：-代表下降, +代表上升.

圖7～10分別表示以目標(biāo)函數(shù)OF1為優(yōu)化目標(biāo)時, 振動力、振動力矩、連桿(2)中點彎曲變形和連桿(3)中點彎曲變形各動力學(xué)指標(biāo)優(yōu)化前后曲線.

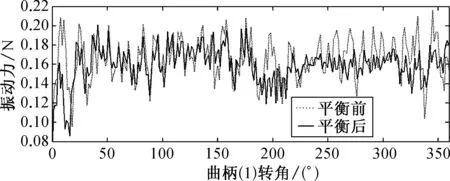
圖7 振動力平衡情況Fig.7 Shaking force balancing

圖8 振動力矩平衡情況Fig.8 Shaking moment balancing

圖9 連桿(2)中點彎曲變形平衡情況Fig.9 Balancing of bending deformation of the midpoint of the connecting rod (2)

圖10 連桿(3)中點彎曲變形平衡情況Fig.10 Balancing of bending deformation of the midpoint of the connecting rod (3)

通過對圖7～10以及表1分析, 可以發(fā)現(xiàn)如下規(guī)律:

(1) 目標(biāo)函數(shù)OF1和OF3均可同時平衡機構(gòu)的振動和構(gòu)件的彈性振動.

(2) 目標(biāo)函數(shù)OF1對機構(gòu)振動的平衡效果優(yōu)于目標(biāo)函數(shù)OF3, 而目標(biāo)函數(shù)OF3對構(gòu)件彈性振動的平衡效果優(yōu)于目標(biāo)函數(shù)OF1.

(3) 目標(biāo)函數(shù)OF2雖然可以改善桿件的彈性振動, 但是會使機構(gòu)的整體振動加劇, 其中, 振動力最大幅值增大了11.29%. 所以, 不能盲目地按照目標(biāo)函數(shù)OF2來優(yōu)化構(gòu)件的彈性振動, 需與機構(gòu)的振動同時優(yōu)化.

因此, 若機構(gòu)振動是主要平衡目標(biāo), 則可以單獨以機構(gòu)振動為優(yōu)化目標(biāo)；若構(gòu)件彈性振動是主要平衡目標(biāo), 則需將機構(gòu)振動和構(gòu)件彈性振動二者綜合為優(yōu)化目標(biāo).

3 結(jié) 語

本文首先采用SPACAR軟件直接建立平面彈性五桿機構(gòu)的有限元模型, 對其進行動力學(xué)仿真分析. 結(jié)果發(fā)現(xiàn), 隨著曲柄轉(zhuǎn)速的不斷增加, 機構(gòu)的整體振動和構(gòu)件的彈性振動均不斷加劇. 為了使機構(gòu)達到平衡, 利用五次多項式二階導(dǎo)數(shù)連續(xù)曲線擬合出其中一根曲柄的轉(zhuǎn)速, 將機構(gòu)的整體振動、構(gòu)件的彈性振動以及二者的綜合作為3種不同的優(yōu)化目標(biāo), 將SPACAR與Matlab優(yōu)化工具箱結(jié)合, 利用PRSM法對平面彈性五桿機構(gòu)進行平衡優(yōu)化. 優(yōu)化結(jié)果表明: 彈性機構(gòu)動平衡優(yōu)化時, 若機構(gòu)振動是主要平衡目標(biāo), 則單獨以機構(gòu)振動為優(yōu)化目標(biāo), 可以在有效平衡機構(gòu)振動的同時改善構(gòu)件的彈性振動；若構(gòu)件彈性振動是主要平衡目標(biāo), 則需將機構(gòu)振動和構(gòu)件彈性振動二者的綜合作為為優(yōu)化目標(biāo).

[1] 黃永強, 王子良. 連桿機構(gòu)的彈性動力平衡[J].機械工程學(xué)報, 1991, 27(1): 91-97.

[2] 宋軼民, 張策, 余躍慶，等. 彈性連桿機構(gòu)振動控制研究綜述[J].機械工程學(xué)報, 2001, 37(10): 10-13.

[3] YU Y Q, LIN J. Active balancing of a flexible linkage with redundant drives[J]. Journal of Mechanical Design, 2003, 125(1): 119-123.

[4] 蔣斌. 用冗余驅(qū)動方法進行彈性機構(gòu)動力平衡的理論與實驗研究[D].北京: 北京工業(yè)大學(xué)機械工程與應(yīng)用電子技術(shù)學(xué)院, 2003.

[5] 歐玉俊, 孫志宏, 章文俊，等. 基于冗余伺服電機法的彈性連桿機構(gòu)的平衡[J].機械科學(xué)與技術(shù), 2012, 31(9): 1454-1457.

[6] 楊元福. 基于PRSM法的平面彈性五桿機構(gòu)動力學(xué)平衡研究[D].上海: 東華大學(xué)機械工程學(xué)院, 2014.

[7] SUN Z H, ZHANG B, ZHANG W J. Application of partial redundant servomotor approach to shaking balancing of flexible mechanisms: A finite element analysis[C]// The 14th IFToMM World Congress. Taipei, Taiwan, 2015.

[8] 張策. 彈性連桿機構(gòu)的分析與設(shè)計[M].2版. 北京: 機械工業(yè)出版社, 1993.

[9] AARTS R G K M, JONKER J B, VAN DIJK J. Prototype modeling of mechanical systems: An introduction for module 7&8/ Project F [M]. Enschede： University of Twente, 2015.

[10] JONKER J B, MEIJAARD J P. SPACAR-computer program for dynamic analysis of flexible spatial mechanisms and manipulators[M]// W Schiehlen (ed.). Multi-body Systems Handbook. Berlin : Springer-Verlag, 1990: 123-143.

[11] AARTS R G K M, MEIJAARD J P, JONKER J B. SPACAR Manual[M]. Enschede： University of Twente, 2011.

(責(zé)任編輯: 杜 佳)

Vibration Balancing Optimization of Elastic Five-Bar Planar Linkages

JIANGChangyun,SUNZhihong,RAHMANHabibur,CAIWenran,GAOMingyang,WANGHuan,LIUZhi

(College of Mechanical Engineering, Donghua University, Shanghai 201620, China)

An elastic five-bar finite model is directly established with the SPACAR program and the dynamic simulation analysis is discussed in the Matlab environment. Increasing gradually the speed of the cranks, the simulation results show that the shaking of the whole mechanism and the vibration of the elastic bars are continually aggrandized. Regarding the shaking of the mechanism, the vibration of two connecting rods and the integrated function of both as three different optimization goals, the dynamic property of the elastic five-bar linkages is optimized based on partial redundant servo motor (PRSM) approach, and then the optimization results of three different goals are analyzed. Taking comprehensive analyses into account, the conclusion is firmly achieved. On one hand, considering the vibration of linkages as the objective function, it is possible to decrease the elastic vibration of bars, yet the shaking is intensified in the meantime. On the other hand, with shaking moment or the integrated function of both as the objective function, both the vibration and the shaking can be diminished at the same time, while the effect of the former on balancing of the shaking is better.

five-bar linkages; elastic; balancing; dynamics; partial redundant servo motor(PRSM)approach

1671-0444 (2017)03-0425-05

2016-05-04

江長云(1992—)，女，河南信陽人，碩士研究生，研究方向為機械設(shè)計及理論. E-mail:chyjiang23@126.com 孫志宏(聯(lián)系人)，女，教授， E-mail：zhsun@dhu.edu.cn

TH 113.25

A