基于穩定性理論的張力腿平臺橫搖固有周期分析
吳 昊,林 焰
(大連理工大學 工業裝備與結構分析國家重點實驗室;運載工程與力學學部 船舶工程學院,遼寧大連 116024)
基于穩定性理論的張力腿平臺橫搖固有周期分析
吳 昊,林 焰
(大連理工大學 工業裝備與結構分析國家重點實驗室;運載工程與力學學部 船舶工程學院,遼寧大連 116024)
文章以穩定性理論為基礎提出了一種張力腿平臺橫搖固有周期計算模型,分析了橫搖臨界角對平臺橫搖穩定性的影響,并將其應用于分析平臺設計參數對橫搖固有周期的影響。提出在一個橫搖周期里,最后穩定橫搖臨界角對應的時間歷程為1/4橫搖固有周期這一假設,基于此假設,編制計算機計算程序,計算橫搖運動中每一個橫搖角,判斷其穩定性,找出一個橫搖周期內最后穩定橫搖臨界角對應的時間歷程,求解橫搖運動固有周期。考慮兩種橫搖阻尼情況,計算不同初始橫搖角、橫搖下沉位移、張力腱長度、平臺重量和橫搖阻尼的橫搖固有周期,論證了平臺設計參數對橫搖固有周期的影響。該計算模型克服了從結構角度計算固有周期工作量大、計算周期長、計算結果不可靠的弱點,使橫搖固有周期計算簡單、有效。通過與不考慮橫搖阻尼的情況對比,分析了橫搖阻尼對橫搖固有周期的影響。可以快速計算處于設計階段或者已服役張力腿平臺橫搖固有周期。結合一型設計中的張力腿平臺,應用文中提出的橫搖固有周期計算模型對該平臺進行了橫搖固有周期的計算,并且分析了平臺參數對橫搖固有周期的影響。結果表明該方法可以對張力腿平臺橫搖固有周期進行快速計算。并可推廣應用于其它海上結構物的橫搖固有周期計算。
張力腿平臺;橫搖;穩定性;臨界角;固有周期
0 引 言
石油是經濟的血液,擁有充足的油氣資源,并且保證油氣資源的穩定供給,是經濟平穩發展的必要條件。進入21世紀以來,隨著社會和經濟的發展,世界已經逐漸步入能源稀缺時代。陸上資源開發難度越來越大,許多國家把目光轉向海洋[1]。海洋環境的復雜多變,波浪和風的無序性,對海洋結構物的運動有很大影響,甚至威脅它們的安全。海洋環境施加在海洋結構物上的載荷影響著海洋結構物的運動。海洋結構物在海洋中有6個自由度的運動,分別是:ξ1縱蕩、ξ2升沉、ξ3橫蕩、ξ4橫搖、ξ5首搖和ξ6縱搖。橫搖運動對于張力腿平臺在作業工況和自存工況的穩定性有著重要影響。對于張力腿平臺,水平面結構近似對稱,在不考慮橫搖和縱搖慣性矩不同的情況下,ξ4橫搖運動和ξ6縱搖運動近似相同。本文主要討論ξ4橫搖運動。
1 研究現狀
Virgin[2]描述了一個數值和現象學相結合的方法來分析橫搖運動,非線性阻尼和復原力臂特性。參照定性預測技術對周期運動的穩定性,特別是傾覆的可能性進行了探索。規則橫浪中混沌運動現象是一個新的特征,應該引起設計師的興趣。例如攝動技術,利用動力學系統理論指導下的數值模擬檢測混沌現象是正當的,這是傳統定量方法的局限性。Soliman等[3]做了一個經典的研究。該研究提出了半經驗非線性微分方程的穩態和瞬態解,并將其應用于模擬在海軍建造文獻中被廣泛討論的兩艘沉船的共振橫搖運動。起始條件的空間安全區域的分析表明,瞬態傾覆可以在最后穩定運動狀態是穩定性喪失的對應波高的一小部分時發生。該安全區域在中部區域的侵蝕非常突然,這意味著瞬間傾覆可能是一個合理的可重復的現象,提供了一種新的方法來量化船在波浪中的穩定性。Lin等[4]開發了隨機分析程序,研究受到隨機噪聲干擾的周期性激勵作用的混沌橫搖運動和船舶傾覆的性質。數值結果表明,在噪聲的情況下,船舶所有在異宿軌道附近的橫搖運動軌跡將最終導致傾覆。Taylan[5]利用靜穩性和非線性動力學穩定性提出了被稱為“穩性儲備”或者“穩性裕度”兩種相對不同的方法,分析船舶流體力學。為了實現這個目的,橫浪中的非線性橫搖模型已經實現。根據分析的結果,提出了改善在海浪中船舶穩定性的建議。谷家揚等[6]對隨機波浪下的張力腿平臺耦合響應進了研究。用龍格—庫塔方法解時域運動方程。Jonswap譜通過線性插值模擬隨機波浪和流,風譜使用NPD譜。用蒙特卡羅方法模擬隨機波和風的波動。
許多學者對張力腿平臺在海洋中的運動進行了廣泛而富有成效的研究。橫搖運動和傾覆的研究主要集中在船舶領域,海洋結構物的橫搖運動和傾覆的研究很少,特別是關于張力腿平臺的橫搖運動和傾覆研究很少。本文主要研究張力腿平臺橫搖穩定性以及橫搖固有周期。
2 橫搖運動模型
張力腿平臺在海洋中受到外界載荷的激勵作用,產生ξ1縱蕩、ξ2升沉、ξ3橫蕩、ξ4橫搖、ξ5首搖和ξ6縱搖六個自由度的運動。
對于張力腿平臺,張力腱的預張緊力平衡平臺浮力與重力之間的差值,橫搖運動往往伴隨橫蕩運動,橫搖運動會引起平臺升沉運動。張力腿平臺水平面的結構近似對稱,不考慮橫搖和縱搖慣性矩不同,ξ4橫搖運動和ξ6縱搖運動近似相同。本文主要研究ξ4橫搖運動。海洋結構物受到波浪和風等外界載荷擾動,一般非線性微分橫搖方程如下:
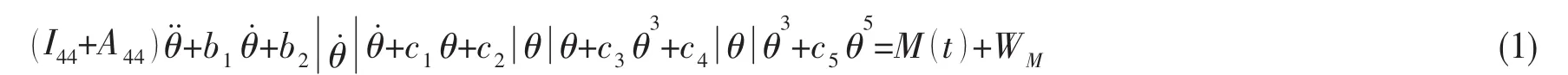
式中:Θ是橫搖角,rad;I44是橫搖慣性力矩,N·m;A44是水動力引起的附加慣性力矩,N·m;b1,b2,c1,c2,c3,c4和c5是系數;M()t是擾動力矩,N·m;WM是風傾力矩,N·m。
3 張力腿平臺橫搖固有周期計算
張力腿平臺在海洋中受到浮力、重力和張力腱的預張緊力的作用產生ξ1縱蕩、ξ2升沉、ξ3橫蕩、ξ4橫搖、ξ5首搖和ξ6縱搖六個自由度的運動。平臺所受浮力與排開水的體積成正比,平臺在海洋中的浮力體為半浸沒的圓柱形立柱和全浸沒的長方形橫撐,是規則體,正常作業工況下排水體積與平臺升沉位移成正比,所以可以用彈簧k表示平臺升沉位移與浮力之間的關系,平臺位移向下,浮力增大,等效彈簧拉力增大;平臺位移向上,浮力減小,等效彈簧拉力減小。正常作業工況下張力腱張緊,張力腱內部存在預張緊力,考慮張力腱彈性系數為線形,預張緊力與拉伸位移成正比,即預張緊力與平臺升沉位移成正比,所以可以用彈簧k1表示平臺升沉位移與預張緊力之間的關系,平臺位移向下,預張緊程度減小,張力腱的預張緊力減小;平臺位移向上,預張緊程度增大,張力腱的預張緊力變大。張力腿平臺在四組張力腱的約束下在海洋中運動,運動中張力腱長度變化與張力腱原長相比很小,可以忽略運動中的四組張力腱長度的不同。橫搖運動是繞軸轉動,平臺水平面近似對稱,橫搖運動中有相同橫搖轉角的兩組張力腱拉伸位移近似相同,橫搖轉角兩側的兩組張力腱拉伸位移不同,所以可將張力腿平臺橫搖運動所受外力簡化為兩組拉伸位移不同的彈簧k1和彈簧k。
將張力腿平臺簡化為質點M,兩組彈簧k1等效平臺所受張力腱的預張緊力,彈簧k等效平臺所受浮力。所以可以用質點M、兩組彈簧k1和彈簧k模擬張力腿平臺真實橫搖運動和受力。張力腿平臺橫搖運動模型如圖1所示。本文分析兩種橫搖運動,一種是考慮橫搖阻尼的橫搖運動,另一種是不考慮橫搖阻尼的橫搖運動。
在圖1建立的橫搖運動模型基礎上,應用穩定性理論中臨界點、中心點和鞍狀點概念,提出一種張力腿平臺橫搖固有周期計算模型。該橫搖固有周期計算模型原理為:在一個橫搖運動周期的前1/4歷程,橫搖過程的任何一個角度都可能為橫搖臨界角。橫搖臨界角可能為穩定的中心點,也可能為不穩定的鞍狀點。在穩定性理論中,一個橫搖運動周期內,橫搖臨界角如果為中心點,橫搖運動在此時刻穩定,繼續運動到下一時刻;如果下一時刻橫搖臨界角為鞍狀點,橫搖運動在此時刻不穩定,說明此時刻橫搖運動的前1/4周期已結束。基于此橫搖運動穩定性分析,提出在一個橫搖周期里,最后穩定橫搖臨界角對應的時間歷程為1/4橫搖固有周期這一假設。基于此假設,編制計算機計算程序,計算橫搖運動中每一個橫搖角,判斷其穩定性,找出一個橫搖周期內最后穩定橫搖臨界角對應的時間歷程,求解橫搖運動固有周期。張力腿平臺橫搖固有周期計算模型計算流程如下:
(1)建立張力腿平臺橫搖運動方程;
(2)求解橫搖臨界角,判斷臨界角的穩定性;
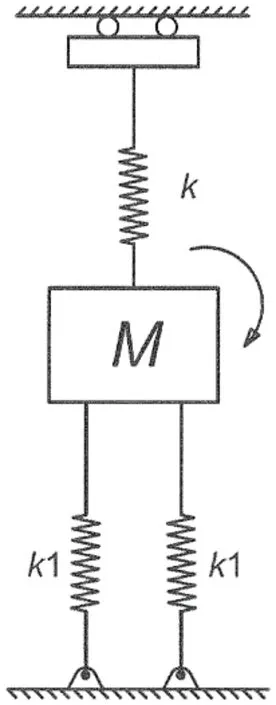
圖1 張力腿平臺橫搖運動模型Fig.1 TLP roll motion model
(3)確定橫搖臨界角最終穩定時間;
(4)橫搖臨界角最終穩定時間為一次橫搖運動的1/4固有周期,求解張力腿平臺橫搖固有周期。張力腿平臺橫搖固有周期計算流程圖如圖2所示。
3.1 考慮橫搖阻尼的張力腿平臺橫搖運動
對于張力腿平臺橫搖運動,橫搖位移正比于橫搖角,橫搖阻尼為非線性。二次非線性是最簡單的高階非線性,假設平臺橫搖阻尼與橫搖角速度的平方成正比。
3.1.1 張力腿平臺橫搖運動方程及
臨界角計算
考慮二次非線性橫搖阻尼,建立張力腿平臺橫搖方程,如下:
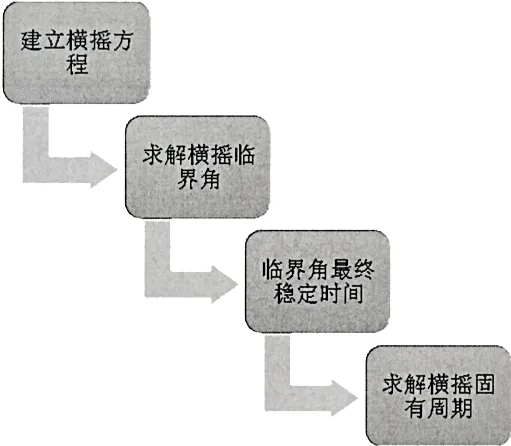
圖2 張力腿平臺橫搖固有周期計算流程圖Fig.2 Flowchartofrolling naturalperiod of TLP
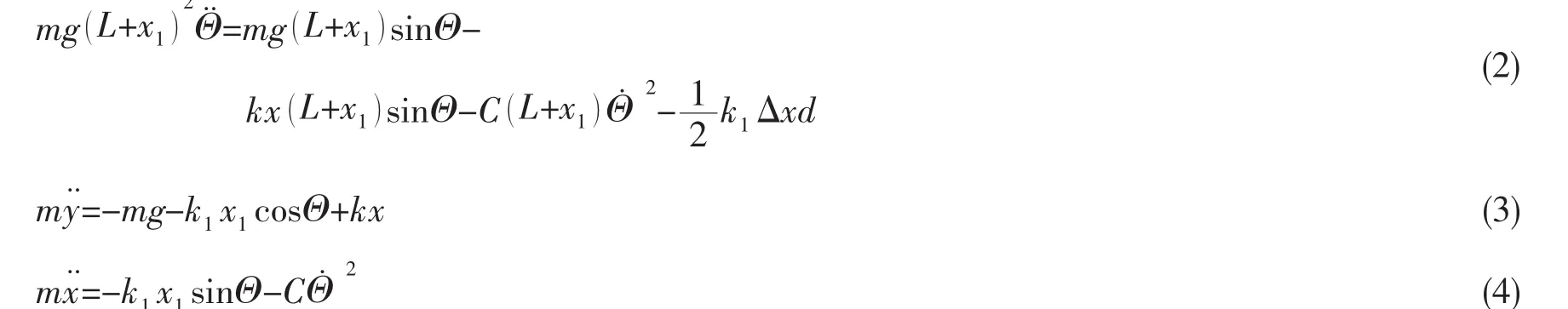
式中:C為橫搖阻尼系數,N/rad;k為浮力系數,N/m;k1為張力腱彈性系數,N/m;x為平臺橫搖下沉位移,m;t為時間,s;△x為橫搖引起的兩組張力腱長度差值,m;d為兩組張力腱水平距離,m;L為張力腱長度,m;G=mg為平臺重量,N。
張力腿平臺張力腱長度遠遠大于△x,忽略各組張力腱長度不同對橫搖運動的影響。通過橫搖方程求解橫搖角θ。在臨界角時,橫搖角θ的角速度Θ˙為0,角加速度Θ¨最大。令

令f=0,求臨界角。解得臨界角方程為:

橫搖角Θ是時間的函數。橫搖角Θ隨著橫搖運動在時間上累積。解得橫搖臨界角θ為:

式中:a為初始橫搖角系數,即通解常數。t為時間,s。
初始橫搖角系數a決定了平臺在橫搖初始時刻的位置,和初始時刻的橫搖角速度。由橫搖角表達式可知角加速度為常數,所以初始橫搖角系數a不決定角加速度。臨界角θ為通解,需要初始邊界條件確定初始橫搖角系數a,解得特解。任何位置都可以是平臺在橫搖前的初始位置,所以不能解得初始橫搖角系數a具體數值。由初始時刻橫搖角小于90°解得a∈ [-2.506 6,2.5066]。且初始橫搖角系數a越接近0,初始橫搖角越小。
3.1.2 張力腿平臺橫搖臨界角穩定性的判斷
f對θ求導,得:

本文結合流花16-2張力腿平臺,論證張力腿平臺橫搖穩定性和計算橫搖固有周期。平臺重量及載荷約為43 188t,立柱結構尺寸如圖3所示。
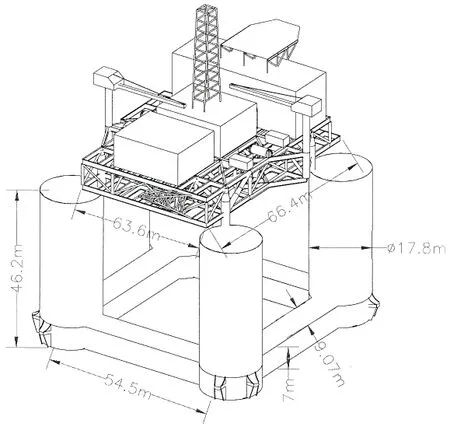
圖3 張力腿平臺結構尺寸Fig.3 Size of TLP
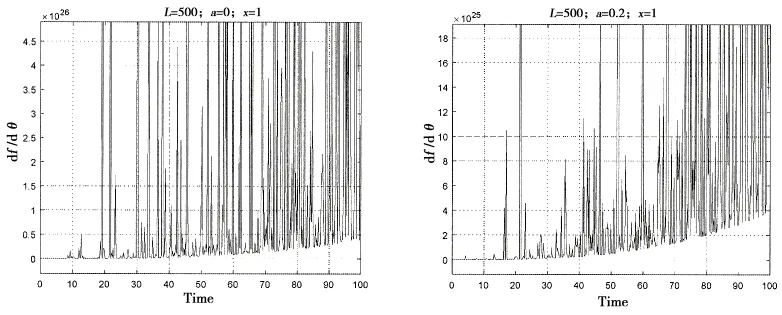

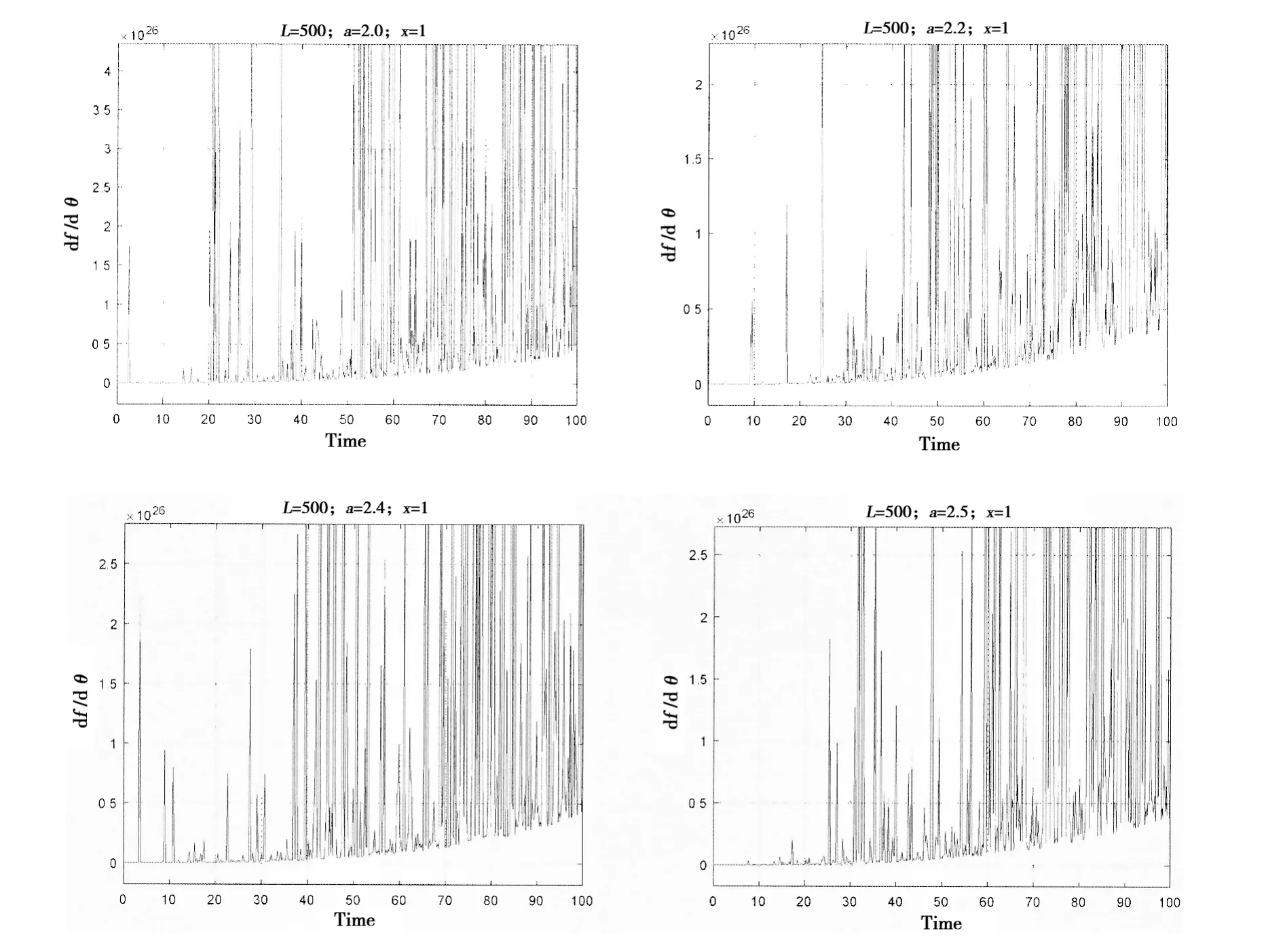
圖4 張力腿平臺橫搖臨界角時間歷程數值模擬曲線(L=500 m,x=1 m)Fig.4 TLP times courses numerical simulation of parametric roll critical points(L=500 m,x=1 m)
張力腿平臺橫搖臨界角時間歷程數值模擬曲線圖,如圖4和圖5所示。
固定橫搖下沉位移x,改變初始橫搖角系數a。
固定初始橫搖角系數a,改變橫搖下沉位移x。
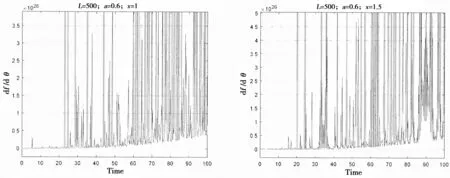

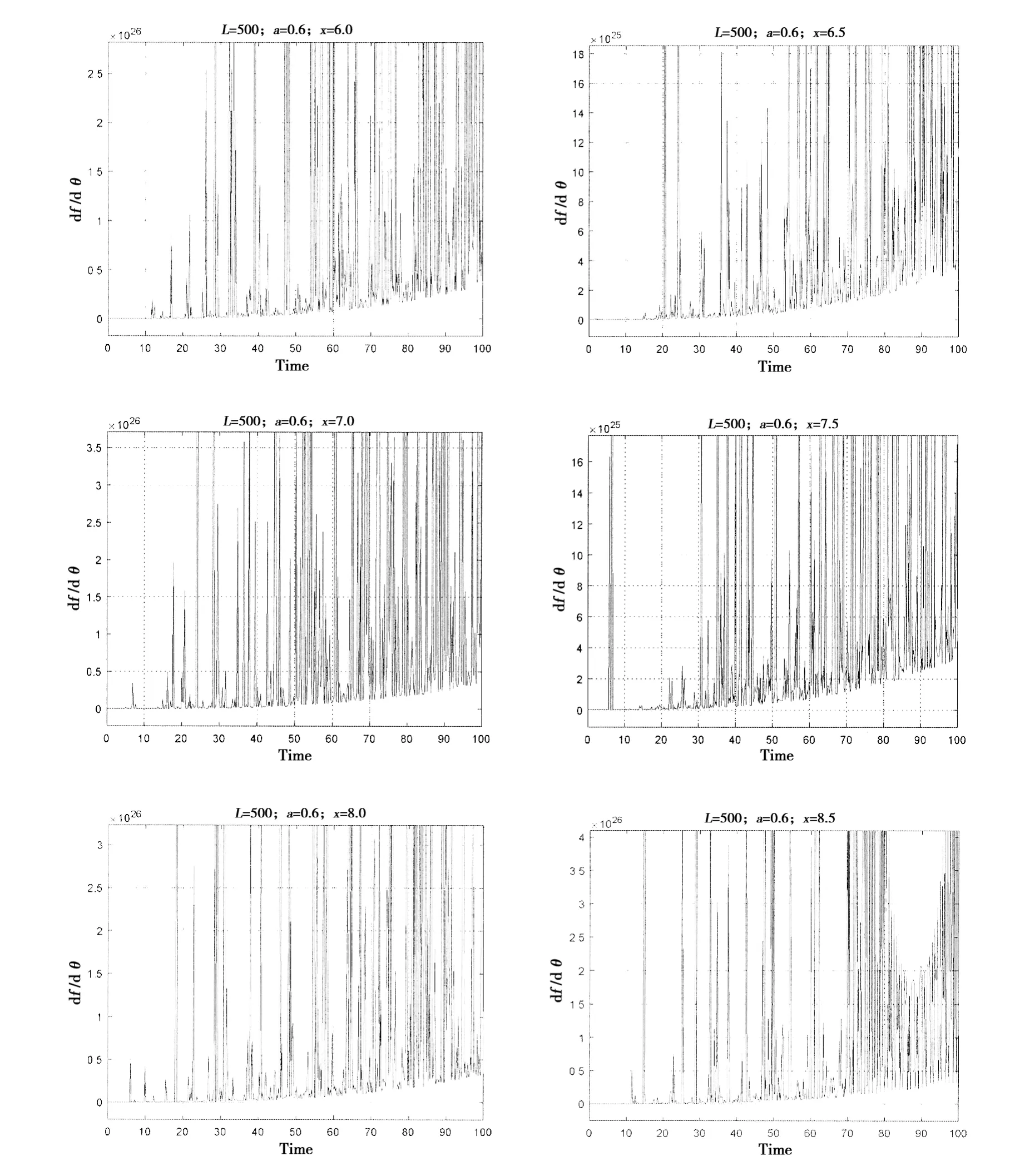
圖5 張力腿平臺橫搖臨界角時間歷程數值模擬曲線 (L=500 m,a=0.6)Fig.5 TLP times courses numerical simulation of parametric roll critical points(L=500 m,a=0.6)
從圖4和圖5數值模擬曲線中可以看到,有限時間內,隨著時間的累積,橫搖角的在負值與正值之間震蕩。說明橫搖臨界角在中心點和鞍狀點之間轉換,橫搖臨界角在穩定與不穩定之間轉換。平臺不能在平衡位置周期性橫搖,橫搖路徑隨著外界擾動的不同而不同。橫搖初始階段,值為負值且近似為0,說明平臺處于外界力干擾很小的穩定狀態,其橫搖狀態主要由稍后的外界擾動作用決定。隨著橫搖過程在時間上的累積,在正值與負值之間震蕩,橫搖臨界角在中心點和鞍狀點之間轉換,橫搖臨界角在穩定與不穩定之間轉換,平臺可能在不是平衡位置的某點達到平衡。當時間經過累積后,大部分工況的橫搖角的這些點為鞍狀點,平臺橫搖不穩定,平臺對應的運動狀態可能已經傾覆。所以張力腿平臺的橫搖運動非常復雜,不能用理論公式預測其平衡位置,只能用頻域或者時域的方法來模擬橫搖運動狀態。
3.1.3張力腿平臺橫搖固有周期計算
在單自由度質點彈簧運動系統里,質點的運動終止點為回復力最大的時刻。在時間歷程中,當質點的加速度達到最大值或者局部極大值時,此刻質點速度最小,等于零,質點位移為最大。對于張力腿平臺的一次橫搖運動,橫搖角加速度為最大值或者局部極大值時,此刻平臺橫搖角速度為最小,等于零,橫搖角最大,平臺橫搖運動達到最大幅值,此時間歷程為平臺橫搖運動周期。其所對應的時間即為橫搖運動固有周期。由計算機程序繪制的橫搖臨界角時間歷程數值模擬曲線圖,當達到此時間歷程中最后一個負值時,說明橫搖達到最后的穩定點,該點可作為橫搖的固有周期處理。由此可求得平臺的橫搖固有周期。橫搖固有周期T計算公式如下:

式中:T為橫搖固有周期,s;tln為橫搖臨界角時間歷程數值模擬曲線的時間歷程中最后一個負值時刻,s。
3.1.4 張力腿平臺設計參數對橫搖固有周期的影響
由橫搖固有周期T計算公式可獲得不同平臺參數下橫搖固有周期數值。
改變平臺設計參數,求得平臺橫搖最后穩定點的時間歷程,求解橫搖固有周期,繪出不同平臺參數對橫搖固有周期的影響曲線。經過分析,對張力腿平臺橫搖固有周期有影響的設計參數有:初始橫搖角、橫搖下沉位移、張力腱長度、平臺重量和橫搖阻尼。
改變平臺橫搖下沉位移x,得到不同初始橫搖角系數a值下最后穩定點對應的時間歷程曲線,如圖6所示。
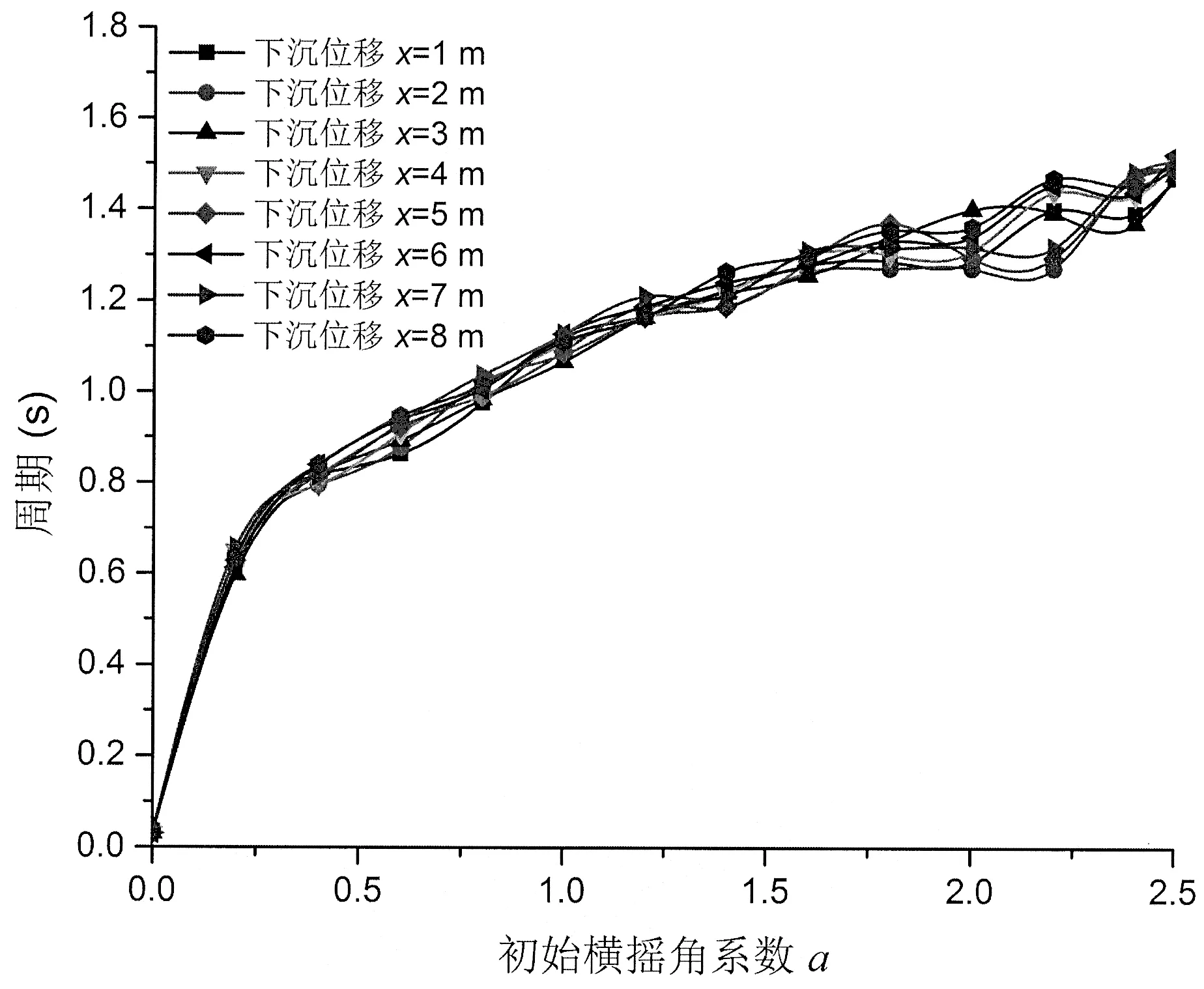
圖6 不同平臺橫搖下沉位移x對橫搖固有周期影響曲線Fig.6 The effects of different displacement of roll subsidence x on rolling natural period
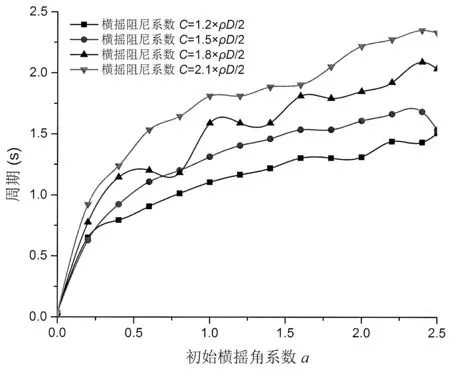
從圖6中可以看出,隨著初始橫搖角系數a的增大,橫搖固有周期逐漸增大。當a=0,橫搖固有周期很小,但是不為零。當0 改變平臺張力腱長度L,得到不同初始橫搖角系數a值下最后穩定點對應的時間歷程曲線,如圖7所示。 圖7 不同張力腱長度對橫搖固有周期影響曲線Fig.7 The effects ofdifferentlength oftendon L on rolling natural period 從圖7中可以看出,隨著初始橫搖角系數a的增大,橫搖固有周期逐漸增大。張力腱長度對橫搖固有周期影響很小。當0 改變平臺重量G,得到不同初始橫搖角系數a值下最后穩定點對應的時間歷程曲線,如圖8所示。 從圖8中可以看出,隨著初始橫搖角系數a的增大,橫搖固有周期逐漸增大。平臺重量對橫搖固有周期影響比較大。當0 改變平臺橫搖阻尼系數C,得到不同初始橫搖角系數a值下最后穩定點對應的時間歷程曲線,如圖9所示。 從圖9中可以看出,隨著初始橫搖角系數a的增大,橫搖固有周期逐漸增大。橫搖阻尼系數C對橫搖固有周期影響很大。當0 圖8 不同平臺重量對橫搖固有周期影響曲線Fig.8 The effects of different weight G on rolling natural period 圖9 不同橫搖阻尼系數對橫搖固有周期影響曲線Fig.9 The effects of different roll damping coefficient C on rolling natural period 3.2 考慮無橫搖阻尼的張力腿平臺橫搖運動 3.2.1 張力腿平臺橫搖運動方程及臨界角計算當平臺橫搖沒有阻尼時,建立張力腿平臺橫搖方程,如下: 式中:k為浮力系數,N/m;k1為張力腱彈性系數,N/m;x為平臺橫搖下沉位移,m;t為時間,s;△x為橫搖引起的兩組張力腱長度差值,m;d為兩組張力腱水平距離,m;L為張力腱長度,m;G=mg為平臺重量,N。 張力腿平臺張力腱長度遠遠大于△x,忽略各組張力腱長度不同對橫搖運動的影響。通過橫搖公式求解橫搖角θ。在臨界角時,橫搖角θ的角速度Θ˙為0,角加速度Θ¨最大。令 令f=0,求臨界角。 解得臨界角方程為: 橫搖角θ是時間的函數。由于橫搖運動,橫搖角θ是時間的累積量。解得橫搖臨界角θ為 式中:a為初始橫搖角系數,即通解常數;t為時間,s。 初始橫搖角系數a決定了張力腿平臺在橫搖初始時刻的位置,和初始時刻的橫搖角速度。由橫搖角表達式可知角加速度為常數,所以初始橫搖角系數a不決定角加速度。橫搖臨界角θ為通解,需要初始邊界條件確定初始橫搖角系數a,解得特解。任何位置都可以是平臺在橫搖前的初始位置,所以不能解得初始橫搖角系數a具體數值。初始橫搖角系數a越接近0,初始橫搖角越小。 3.2.2 張力腿平臺橫搖臨界角穩定性的判斷 f對θ求導,得: 3.2.3 張力腿平臺橫搖固有周期計算 本文以穩定性理論為基礎提出了一種張力腿平臺橫搖固有周期計算模型,分析了橫搖臨界角對平臺橫搖穩定性的影響,并將其應用于分析平臺參數對橫搖固有周期的影響。提出在一個橫搖周期里,最后穩定橫搖臨界角對應的時間歷程為1/4橫搖固有周期這一假設,基于此假設,編制計算機計算程序,計算橫搖運動中每一個橫搖角,判斷其穩定性,找出一個橫搖周期內最后穩定橫搖臨界角對應的時間歷程,求解橫搖運動固有周期。結合一型設計中的張力腿平臺,考慮兩種橫搖阻尼情況,計算不同初始橫搖角、橫搖下沉位移、張力腱長度、平臺重量、橫搖阻尼的橫搖固有周期,論證了平臺參數對橫搖固有周期的影響,對平臺的設計提出了建設性的意見。論證結論如下: (1)此型張力腿平臺橫搖固有周期小于2.4s。 (2)論證了平臺參數對橫搖固有周期的影響。論證了平臺橫搖下沉位移,初始橫搖角,張力腱長度,平臺重量,阻尼系數對橫搖固有周期的影響。 a.平臺橫搖下沉位移的變化對橫搖固有周期的影響較小。初始橫搖角直接影響橫搖固有周期。 b.張力腱長度對橫搖固有周期有影響,但影響不大。 c.平臺重量對橫搖固有周期影響較大。 d.橫搖阻尼對橫搖固有周期影響很大。 (3)利用平臺重量、橫搖阻尼對橫搖固有周期影響不穩定的特性,可以有效避開環境載荷頻率與平臺自身頻率的重合,減少共振的發生。 該橫搖固有周期計算模型克服了從結構角度計算固有周期工作量大、計算周期長、計算結果不可靠的弱點,使橫搖固有周期計算簡單、有效。經過與不考慮橫搖阻尼的情況對比,分析了橫搖阻尼對橫搖固有周期的影響。可以快速計算處于設計階段或者已服役張力腿平臺橫搖固有周期。該方法也可以應用于其他海洋結構物橫搖固有周期計算。 [1]吳 昊,林 焰.張力腿平臺系泊風險評估方法研究[J].船舶力學,2016,20(5):11-14. Wu Hao,Lin Yan.The risk assessment of mooring for tension leg platform[J].Journal of Ship Mechanics,2016,20(5):11-14.. [2]Virgin L N.The nonlinear rolling response of a vessel including chaotic motions leading to capsize in regular seas[J].Applied Ocean Research,1987,9(2):89-95. [3]Soliman M S,Thompson J M.Transient and steady state analysis of capsize phenomena[J].Applied Ocean Research,1991,13(2):82-92. [4]Lin H,Yim S C.Chaotic roll motion and capsize of ships under periodic excitation with random noise[J].Applied Ocean Research,1995,17(3):185-204. [5]Taylan M.Static and dynamic aspects of a capsize phenomenon[J].Ocean Engineering,2003,30(3):331-50. [6]Gu J,Yang J,Lv H.Studies of TLP dynamic response under wind,waves and current[J].China Ocean Engineering,2012, 26:363-378. Analysis rolling natural period for tension leg platform based on stability theory WU Hao,LIN Yan A calculation model was established to research on rolling natural period of Tension Leg Platform (TLP)based on stability theory.The effects of roll critical points on rolling stability and effects of parameters of TLP on rolling natural period were analyzed.And an assumption was put forward that in one rolling motion,times courses corresponding the last stable roll critical point condition is a1/4cycle process.Based on the assumption,computer programs were built to calculate arbitrary roll angle,and used to estimate stability of arbitrary roll angles,so that times courses corresponding the last stable roll critical point in one rolling motion were found.So it can obtain rolling natural period.Considering two conditions of damping, this paper calculated rolling natural period under different initial roll angle,displacement of roll subsidence, length of tendon,weight and roll damping coefficient and demonstrated the influences of parameters of TLP on rolling natural period.The model is simple and effective to support fast estimating rolling natural period whether TLP is in designed stage or in service and avoid to obtain rolling natural period complicated withstructural theory.The influences of roll damping on rolling natural period were demonstrated.Based on a TLP which is in design stage,the rolling natural period was obtained with the established model.In this case,the influence of parameters of TLP on rolling natural period was found.Results show that the model is simple and effective to support fast estimating rolling natural period.This model can also apply to other marine structures to calculate rolling natural period. Tension Leg Platform;roll;stability;critical point;natural period P756.2 A 10.3969/j.issn.1007-7294.2017.07.006 1007-7294(2017)07-0842-14 2017-02-28 吳 昊(1989-),男,博士研究生; 林 焰(1963-),男,教授,博士生導師,E-mail:linyanly@dlut.edu.cn。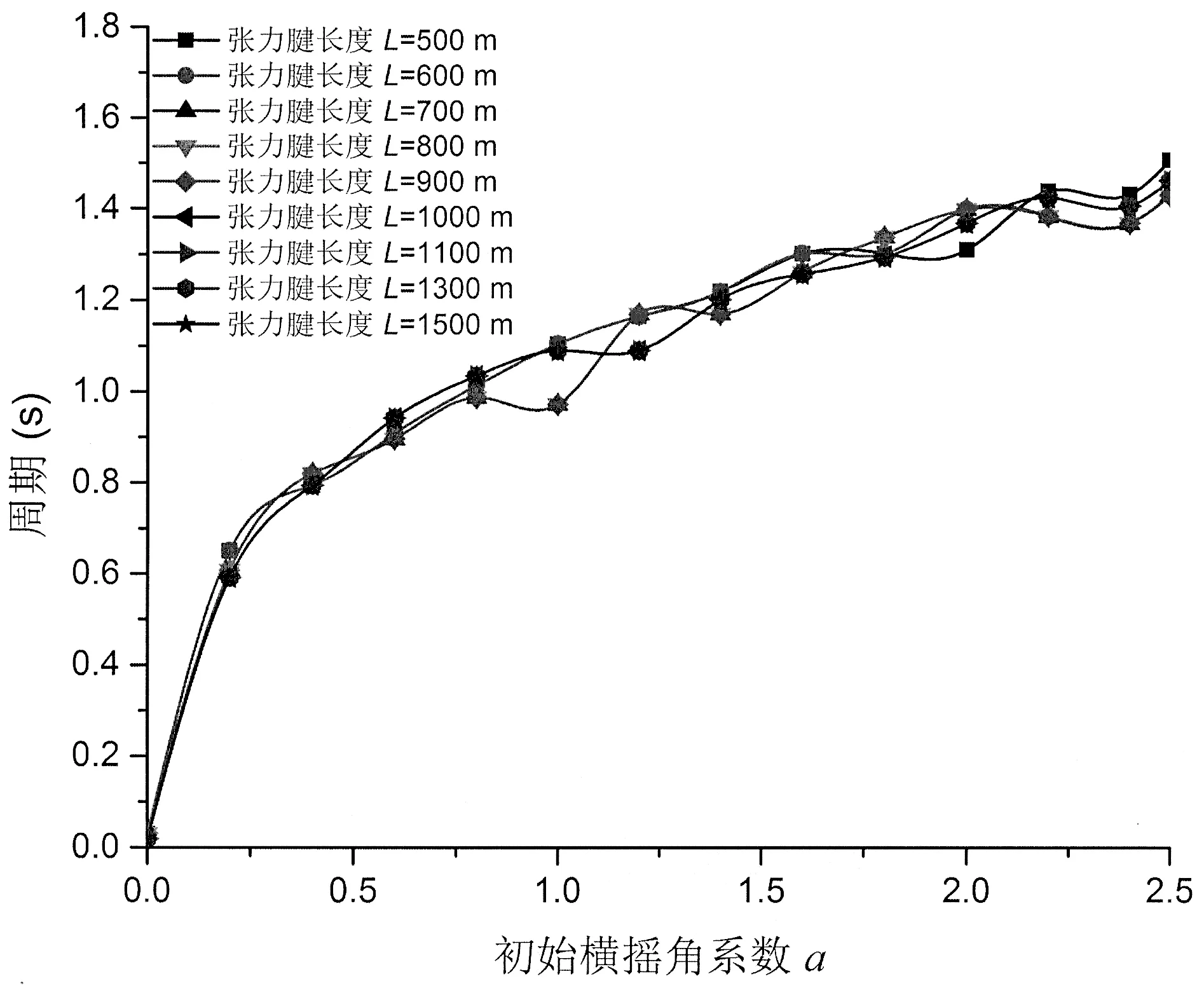

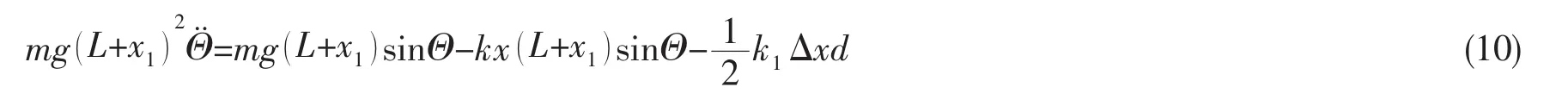





4 結 論
(School of Naval Architecture Engineering,Faculty of Vehicle Engineering and Mechanics,State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116024,China)

