彈性邊界條件下的功能梯度圓柱殼振動特性研究

陳金曉，梁 斌

（河南科技大學 土木工程學院，河南 洛陽 471023）

彈性邊界條件下的功能梯度圓柱殼振動特性研究

陳金曉，梁 斌

（河南科技大學 土木工程學院，河南 洛陽 471023）

文章研究了功能梯度材料圓柱殼在彈性邊界條件下的振動特性。在Flügge理論的基礎上，基于波動法，采用改進傅里葉級數的計算方法建立FGM圓柱殼的振動特征方程，并推導出了彈性邊界條件下FGM圓柱殼的固有頻率參數表達式。通過與兩端簡支條件下的FGM圓柱殼的計算結果進行對比，驗證了文中計算方法的正確性和有效性。通過算例，研究了在約束剛度不斷變化過程中，FGM圓柱殼的固有頻率在不同模態下的變化規律;分析了在彈性邊界條件下，殼體尺寸、體積分數等因素對FGM圓柱殼固有頻率的影響。

彈性邊界；功能梯度材料；圓柱殼；波動法；固有頻率

0 引 言

圓柱殼結構是一種在航空航天、海洋工程等領域廣泛應用的結構形式。考慮功能梯度材料的圓柱殼結構，由于功能梯度材料和圓柱殼的結合，把材料的性能和圓柱殼的優異特性更好的體現出來，功能梯度材料圓柱殼結構也具有了更好的應用價值。因此，研究功能梯度材料圓柱殼在不同情況下的動力學行為特性，對這類結構在實際工程中的安全應用具有非常重要的意義。

目前，關于功能梯度材料圓柱殼在不同邊界條件下的動力性能研究已經取得一些成果。Loy等[1-2]基于經典薄殼理論，利用Rayleigh-Ritz法推導出FGM圓柱殼自由振動的特征方程，研究了在不同邊界條件、體積分數、材料組分等因素下，固有頻率的變化規律曲線。Li等[3-4]在波動法的基礎上，研究了圓柱殼在不同邊界條件下的自由振動特性，并將波動法與其它方法進行對比，發現了波動法在計算上的優越性。Zhu等[5]基于Flügge理論，運用波動法研究了水下圓柱殼的耦合振動特性。Loy等[6]根據Love一階近似理論，研究了兩端簡支、兩端固支、兩端自由等邊界條件下多層圓柱殼的固有頻率變化規律，同時給出了幾種邊界條件下固有頻率的振型。李等[7-8]在Love薄殼理論的基礎上，根據改進的傅里葉級數方法，并結合Rayleigh-Ritz法，研究了彈性邊界條件下旋轉功能梯度材料圓柱殼的自由振動特性，分析了邊界約束剛度、材料組分、殼體尺寸等因素對固有頻率的影響。馬旭等[9]基于波動法，采用改進傅里葉級數方法建立彈性約束邊界條件下圓柱殼的振動模型，研究了圓柱殼在彈性約束邊界條件下的自由振動和強迫振動特性。劉倫等[10]基于Gram-Schmidt正交化建立圓柱殼的振動位移表達式，根據Sanders殼體理論和Rayleigh-Ritz法，在驗證了此方法的正確性的基礎上，研究了邊界各個方向的約束剛度對正交加肋圓柱殼固有頻率的影響。以及其他研究文獻[11-12]。但是由于彈性邊界的復雜性，尚未發現考慮彈性邊界條件下，功能梯度材料圓柱殼振動特性的研究文獻。

本文在Flügge理論的基礎上，采用波動法和改進傅里葉級數方法建立彈性邊界條件下FGM圓柱殼振動頻率的特征方程，運用計算軟件MATLAB求解特征方程得到圓柱殼在彈性邊界下的固有頻率。通過退化計算，將兩端簡支的FGM圓柱殼的固有頻率的計算結果進行對比，驗證了本文計算的有效性和正確性。最后通過算例，探討了不同模態下約束剛度對FGM圓柱殼自由振動的影響，同時研究了在彈性邊界條件下，材料體積分數、殼體尺寸等因素對圓柱殼自由振動的影響。

1 力學模型

圖1所示為圓柱殼的力學模型，R表示平均半徑，L表示圓柱殼長度，h表示圓柱殼壁厚，本文在圓柱殼的中面上建立正交坐標系 x，θ，（ ）z，其中x，θ和z分別為圓柱殼的軸向、環向和徑向坐標。

圖2中所示為彈性邊界約束模型，k0，k1為徑向約束剛度，K0，K1為扭轉約束剛度。通過不同的剛度值組合可以實現所有的邊界條件。例如，當剛度值均為0時,代表自由邊界條件；當扭轉剛度值為0，徑向剛度值為無窮大時，代表兩端簡支邊界條件；當剛度值均為無窮大時，代表兩端固支邊界條件。

假設圓柱殼沿厚度方向的彈性模量與材料組分的百分比有關，則其函數表達式為：

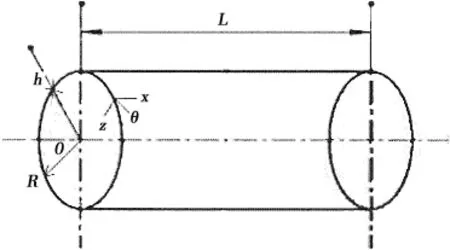
圖1 環肋圓柱殼及其環肋截面模型Fig.1 Geometry of ring-stiffened cylindrical shell and stiffener

其中：V1和V2分別是圓柱殼內、外表面材料的體積百分比，P為冪率指數，其取值范圍為0≤P≤∞。

當圓柱殼的組分材料為兩種時，假定內、外表面材料參數分別為彈性模量E1，E2、質量密度ρ1，ρ2、和泊松比υ1，υ2，環肋FGM圓柱殼的等效彈性模量E，泊松比υ，材料密度ρ表示如下：

圖2 彈性邊界Fig.2 Elastic boundary supports

2 理論推導

根據Flügge理論[11]，圓柱殼的運動方程為：

用波動法表示的圓柱殼振動位移方程如下：

其中：Um，Vm，Wm分別表示x，θ，z方向的波幅，ω表示固有角頻率，km的大小與約束邊界的約束剛度有關，文獻[12]中采用改進傅里葉級數的計算方法求km。

波動法的基本思想是：在圓柱殼的彎曲振動分析中，相應邊界條件下的圓柱殼的軸向波數km可以用梁的彎曲振動波數來替代。梁的運動微分方程為：

式中：DL，ρL，AL代表梁的剛度，密度和橫截面面積。

p（）x是為了克服余弦級數的不連續性而引入的輔助函數。

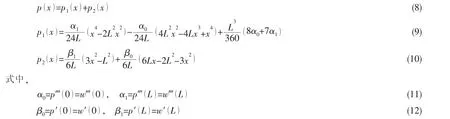
將（7）式代入（6）式得到：

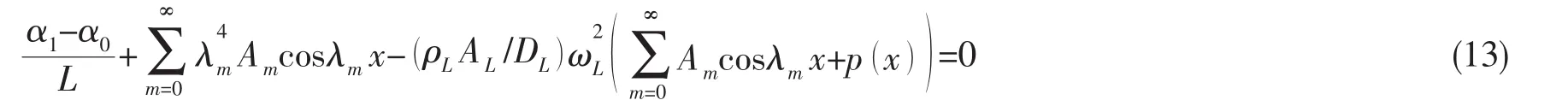
將（13）式進行推導，最終可以化為標準的矩陣求解特征值問題，求解方程可以得到相應的軸向波數。將相應的軸向波數代入（5）式，并將（5）式代入（4）式可以得到用矩陣表示的運動方程，求解運動方程，進而得到圓柱殼的固有頻率。

3 數值計算及分析

3.1 正確性和有效性分析

為了驗證本文研究方法的正確性和有效性，表1給出了兩端簡支條件下功能梯度材料圓柱殼固有頻率的計算結果，并與已有文獻的計算結果進行了對比分析，本文的計算結果與文獻[1]中的計算結果存在著誤差，但均控制在百分之零點幾之內，這個誤差在工程允許的誤差范圍之內。結果分析驗證了本文求解彈性邊界下FGM圓柱殼固有頻率的計算方法的正確性和有效性。表1中計算參數均與文獻[1]中的相同。n表示周向波數。

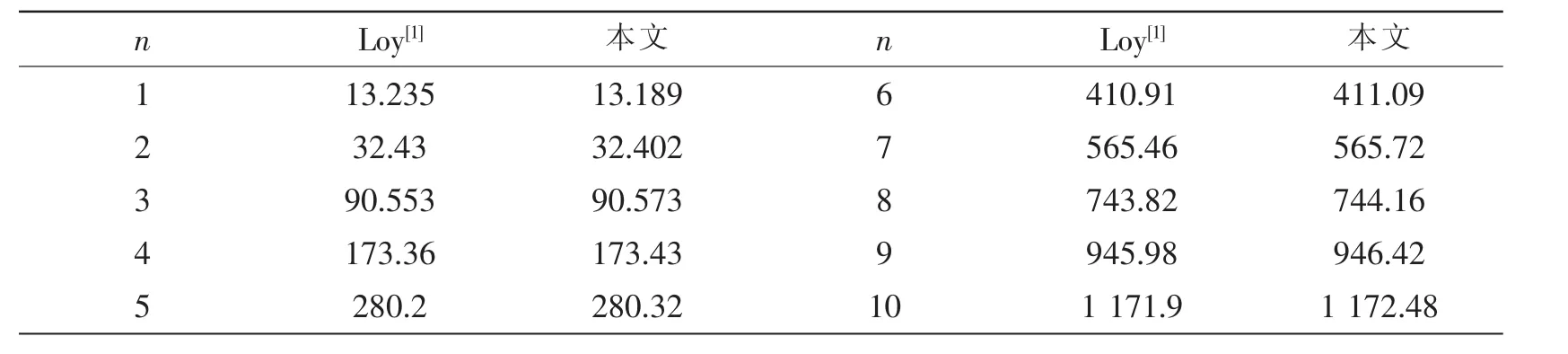
表1 兩端簡支條件下功能梯度材料圓柱殼固有頻率計算結果對比分析Tab.1 Comparison between the results of calculation of the natural frequencies for FGM cylindrical with SS-SS

3.2 邊界剛度對FGM圓柱殼的振動特性的影響

本文通過多組算例研究了彈性邊界條件下FGM圓柱殼的振動特性，在不同邊界約束的情況下，通過改變約束剛度、殼體尺寸、體積分數等因素，分析了圓柱殼固有頻率的變化規律，計算結果見圖3-12。本文算例中，規定圓柱殼的功能梯度材料組分為外表面不銹鋼、內表面氮化硅，不銹鋼和氮化硅的材料參數分別為：E2=2.077 88×1011，υ2=0.317 756，ρ2=8 166；E1=3.222 7×1011，υ1=0.24，ρ1=2 376。文中計算時所選用的參數為：h=0.002，R=1，L=20，m=1，P=1。

為了便于分析，計算過程中均采用無量綱約束剛度（約束剛度值除以彎曲剛度DL），即：k0′=k0/DL，k1′=k1/DL，K0′=K0/DL，K1′=K1/DL。計算中選用兩種邊界約束情況，一種為k0′，k1′為無窮大、K0′，K1′同時從1增大至100 000，即邊界條件從兩端簡支到兩端固支中變化，視為邊界約束A；另一種為k0′，K0′為無窮大、K1′=1、k1′從1增大至100 000，即邊界條件從一端固定、一端自由到一端固定、一端簡支中變化，視為邊界約束B。計算過程中無窮大均取1010。圖3中，約束剛度值均取對數值log k0′，log k1′，log K0′，log K1′表示，其余情況下的約束剛度值均用實際值表示。

3.2.1 約束剛度對FGM圓柱殼固有頻率的影響

圖3和圖4給出了兩種邊界約束情況下，FGM圓柱殼固有頻率在不同n值情況下隨著約束剛度增大的變化規律曲線。可以看出，隨著n值的增大，約束剛度對固有頻率的影響在減弱，當n＞3時，約束剛度對固有頻率的影響并不明顯，基本上可以忽略不計。當n值較小時，兩種邊界約束下的固有頻率均隨著約束剛度的增大先增大后逐漸趨于一個定值。兩種邊界約束情況下，當約束剛度在1～1 000時，隨著約束剛度的增大，固有頻率亦增大，但是在約束剛度在100～1 000時，增大幅度大幅度減小，當約束剛度大于1 000之后，隨著約束剛度的增大，固有頻率的大小已趨于穩定。對比圖3和圖4，在固有頻率增大過程中，邊界約束B時，固有頻率（n=1）的增大幅度更大。在約束剛度一定時，固有頻率隨著n值的增大先減小后增大。

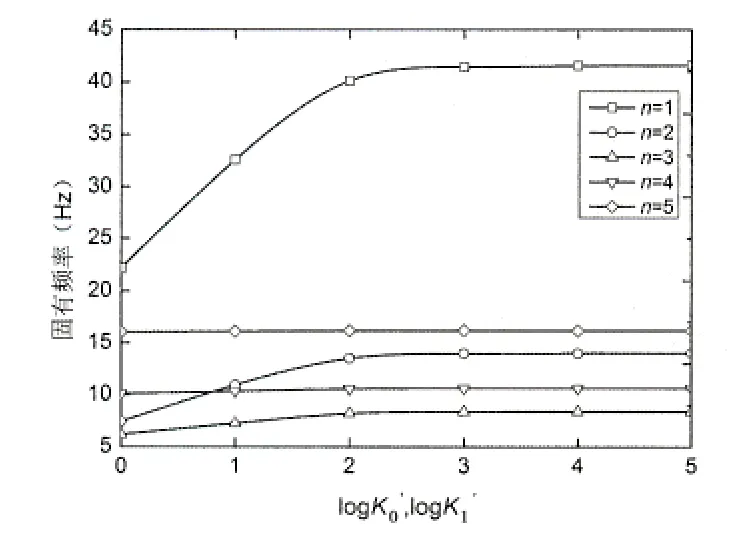
圖3 不同n值下固有頻率變化規律曲線（邊界約束A）Fig.3 Variation of natural frequency with different circumferential wave number (boundary constraints A)

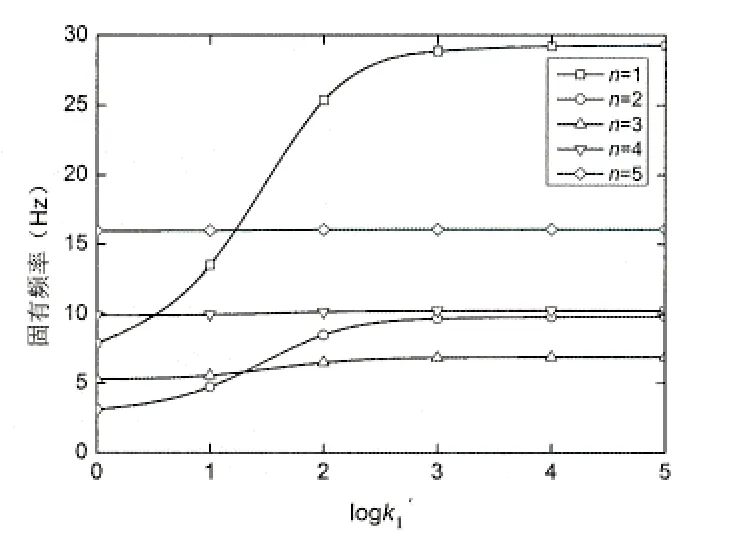
圖4 不同n值下的固有頻率變化規律曲線（邊界約束B）Fig.4 Variation of natural frequency with different circumferential wave number (boundary constraints B)

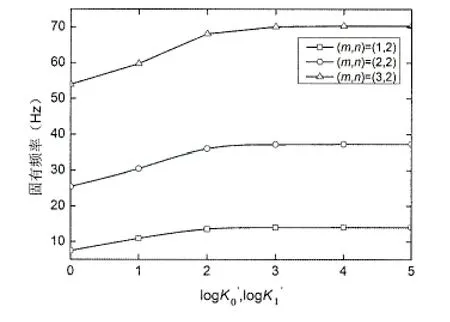
圖5 不同模態下的固有頻率變化規律曲線（邊界約束A）Fig.5 Variation of natural frequency with different modal shapes(boundary constraints A)

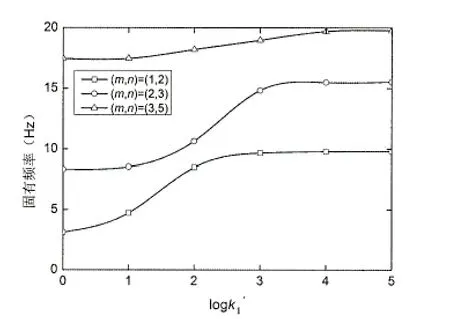
圖6 不同模態下的固有頻率變化規律曲線（邊界約束B）Fig.6 Variation of natural frequency with different modal shapes(boundary constraints B)

圖5和圖6給出了兩種邊界約束情況下，FGM圓柱殼固有頻率在不同模態下隨著約束剛度的增大的變化規律曲線。從圖中可以看出，固有頻率隨著軸向半波數m值的增大而增大，且增大幅度比較明顯。邊界約束A時，隨著約束剛度的增大，三種模態下固有頻率的變化規律大致相同；邊界約束B時，隨著約束剛度的增大，三種模態下固有頻率的變化規律出現了不同，在模態（1，2）時，固有頻率的增大主要出現在k1=1～100時；在模態（2，3）時，固有頻率的增大主要出現在k1=10～1 000時：在模態（3，5）時，固有頻率的增大主要出現在k1=10～10 000時，且是一個緩慢上升的過程，上升幅度比較小。由此可見，在約束剛度增大的過程中，n值對固有頻率的變化規律的影響比m值的大。

3.2.2 FGM圓柱殼在彈性邊界下的自由振動

基于上述結論，以下計算中均取：K0′=10，K1′=10（邊界約束A）；k1′=10（邊界約束B）。圖7和圖8給出了兩種邊界約束情況下，FGM圓柱殼的固有頻率在不同n值時，隨L的增大的變化規律曲線。從圖中可以看出，兩種邊界約束情況下，隨著L的增大，固有頻率的變化規律大致相同：均隨著L的增大而不斷減小，且減小幅度也在不斷地下降；當L從2增大到5時，固有頻率的下降幅度最大；不同的邊界約束條件只是改變了固有頻率的大小。固有頻率均隨著n值的增大先減小后增大（邊界約束B情況下L=2除外），但固有頻率最小時的n值不同；邊界約束B情況下L=2時，固有頻率隨著n值的增大而不斷減小。

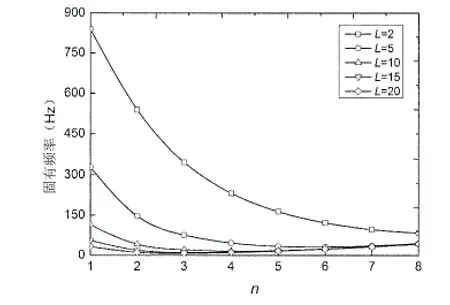
圖7 不同L下的固有頻率變化規律曲線（邊界約束A）Fig.7 Variation of natural frequency with different length of the shell(boundary constraints A)

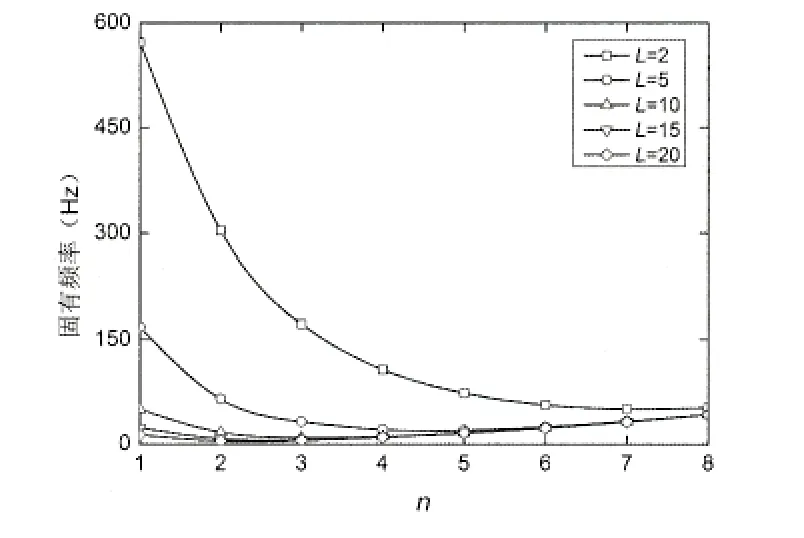
圖8不同L下的固有頻率變化規律曲線（邊界約束B）Fig.8 Variation of natural frequency with different length of the shell(boundary constraints B)

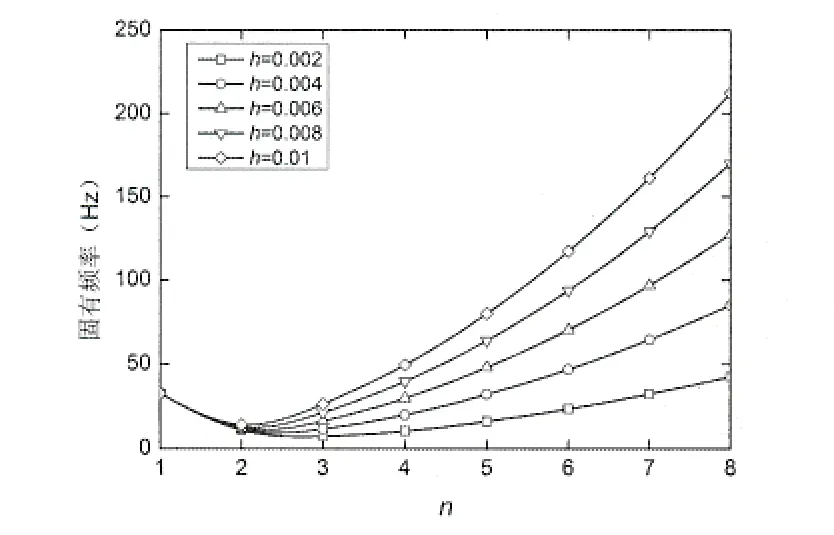
圖9 不同h下的固有頻率變化規律曲線（邊界約束A）Fig.9 Variation of natural frequency with different thickness of the shell(boundary constraints A)

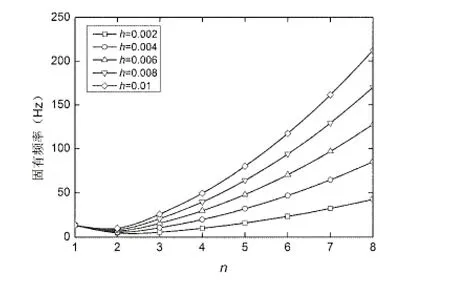
圖10不同h下的固有頻率變化規律曲線（邊界約束B）Fig.10 Variation of natural frequency with different thickness of the shell(boundary constraints B)

圖9 和圖10給出了兩種邊界約束情況下，FGM圓柱殼的固有頻率在不同n值時，隨h的增大的變化規律曲線。從圖中可以看出，固有頻率均隨著h值的增大而增大，但當n=1時這種現象并不明顯。固有頻率均隨著n值的增大先減小后增大，且固有頻率的最小值均出現在n=2時。對比圖9和圖10，在n=1～3時，邊界約束A的固有頻率明顯大于邊界約束B的固有頻率，當n＞3時，邊界約束的改變對固有頻率的影響基本上可以忽略不計。

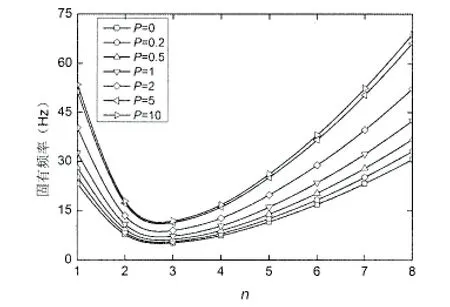
圖11 不同P下的固有頻率變化規律曲線（邊界約束A）Fig.11 Variation of natural frequency with different volume fraction(boundary constraints A)

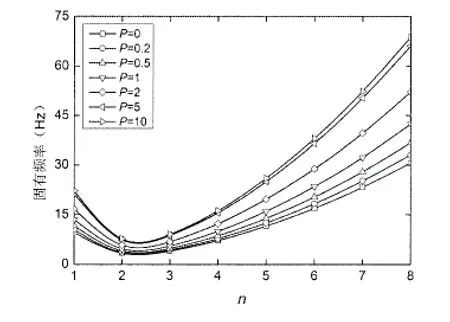
圖12不同P下的固有頻率變化規律曲線（邊界約束B）Fig.12 Variation of natural frequency with different volume fraction(boundary constraints B)

圖11 和圖12給出了兩種邊界約束情況下，FGM圓柱殼的固有頻率在不同n值時，隨P的增大的變化規律曲線。從圖中可以看出，兩種邊界約束有著相似的變化規律，固有頻率均隨著P值的增大而增大；固有頻率均隨著n值的增大先減小后增大，但固有頻率最小時的n值不同，邊界約束A時，n= 3時，固有頻率最小，邊界約束B時，n=2時，固有頻率最小。對比圖11和圖12，邊界約束對固有頻率的影響只是在n=1～3時比較明顯，此時邊界約束A的固有頻率明顯大于邊界約束B的固有頻率，但當n＞3時，這種現象弱化了許多。

4 結 論

（1）固有頻率隨著約束剛度的增大先增大，之后趨于一個定值，且隨著n的增大，約束剛度對固有頻率的影響可以忽略不計。邊界約束情況不同，隨著約束剛度的變化，固有頻率的變化速率差距很大。

（2）在約束剛度一定的情況下，固有頻率隨著m值的增大而增大，隨著n值的增大，固有頻率先減小后增大。不同模態（m，n）下，隨著約束剛度的增大，固有頻率的反應靈敏度不同。

（3）在n值較小時，固有頻率均隨著L的增大而顯著減小；固有頻率隨著h的增大而增大；固有頻率隨著P值的增大而增大。

（4）邊界約束條件對固有頻率的影響只在n值較小的情況下比較明顯，而這種影響只是改變了固有頻率的大小，對固有頻率的變化規律并無太大影響。

[1]Loy C T,Lam K Y,Reddy J N.Vibration of functionally graded cylindrical shells[J].International Journal of Mechanical Sciences,1999,41(3)：309-324.

[2]梁 斌,李 戎,張 偉,等.功能梯度材料圓柱殼的振動特性研究[J].船舶力學,2011,15(1-2)：109-117.Liang B,Li R,Zhang W,et al.Vibration characteristics of functionally graded materials cylindrical shells[J].Journal of Ship Mechanics,2011,15(1-2)：109-117.

[3]Li X B.Study on free vibration analysis of circular cylindrical shells using wave propagation[J].Journal of Sound and Vibration,2008,311(3-5)：667-682.

[4]Zhang X M,Liu G R,Lam K Y.Vibration analysis of thin cylindrical shells using wave propagation approach[J].Journal of Sound and Vibration,2001,239(3)：397-403.

[5]Zhu X,Ye W B,Li T Y,Chen C.The elastic critical pressure prediction of submerged cylindrical shell using wave propagation method[J].Ocean Engineering,2013,58(1)：22-26.

[6]Loy C T,Lam K Y.Effects of boundary conditions on frequencies of a multi-layered cylindrical shell[J].Journal of Sound and Vibration,1995,188(3)：363-384.

[7]李文達,杜敬濤,楊鐵軍,等.彈性邊界約束旋轉功能梯度圓柱殼結構自由振動行波特性分析[J].應用數學和力學,2015,36(7)：710-723.Li W D,Du J T,Yang T J,et al.Traveling wave mode characteristics of rotating functional gradient material cylindrical shell structures with elastic boundary constraints[J].Applied Mathematics and Mechanics,2015,36(7)：710-723.

[8]李文達,杜敬濤,楊鐵軍,等.基于改進傅里葉級數方法的旋轉功能梯度圓柱殼振動特性分析[J].哈爾濱工程大學學報,2016,37(3)：388-393.Li W D,Du J T,Yang T J,et al.Vibration characteristics analysis of the rotating functionally graded cylindrical shell structure using an improved Fourier series method[J].Journal of Harbin Engineering University,2016,37(3)：388-393.

[9]馬 旭,杜敬濤,楊鐵軍,等.基于波傳播方法的邊界條件對圓柱殼振動特性的影響分析[J].振動工程學報,2009,22 (6)：608-613.Ma X,Du J T,Yang T J,et al.Analysis of influence of boundary conditions on cylindrical shell dynamics based on wave propagation approach[J].Journal of Vibration Engineering,2009,22(6)：608-613.

[10]劉 倫,曹登慶,孫述鵬,等.彈性邊界約束的正交加肋圓柱殼振動特性分析[J].船舶力學,2016,20(8)：1016-1027.Liu L,Cao D Q,Sun S P,et al.Vibration analysis of orthogonal stiffened cylindrical shells constrained by elastic boundary[J].Jounalof Ship Mechanics,2016,20(8)：1016-1027.

[11]Flügge W.Stresses in shells[M].Springer,New York,1973.

[12]Li W L.Free vibration of beams with generalboundary conditions[J].Journal of Sound and Vibration,2000,237(4)：709-725.

Study on the vibration of functionally graded material cylindrical shells under elastic boundary conditions

CHEN Jin-xiao,LIANG Bin
(Civil Engineering School,Henan University of Science and Technology,Luoyang 471023,China)

The free vibration characteristics of functionally graded material(FGM)cylindrical shells under elastic boundary conditions is studied.Based on the Flügge theory,the vibration characteristic equations of FGM cylindricalshells is derived by wave method and Fourier series,and the frequency parameter expression of FGM cylindrical shells under elastic boundary conditions is obtained.The present analysis is validated by comparing results with FGM cylindrical shells with simply supported-simply supported(SS-SS).By numerical examples,the varying regularity of natural frequency change for FGM cylindrical shells under different mode with the elastic stiffness constantly changing is studied,and the effects of shell size,volume fraction on the natural frequencies of FGM cylindrical shell are illustrated.

elastic boundary;functionally graded material;cylindrical shell;wave method; natural frequency

TB535+.1

A

10.3969/j.issn.1007-7294.2017.07.010

1007-7294（2017）07-0880-08

2017-03-05

國家自然科學基金資助項目（51105132；11402077）；河南省自然科學基金項目（編號122300410112）

陳金曉（1991-），女，碩士研究生，E-mail：chenjinxiao0520@163.com；

梁 斌（1963-），男，教授，博士生導師，E-mail：liangbin4231@163.com。