高中數學“問題導學”教學模式的嘗試
李帶兵
(江蘇省南通大學附屬中學,江蘇 南通 226000)
?
高中數學“問題導學”教學模式的嘗試
李帶兵
(江蘇省南通大學附屬中學,江蘇 南通 226000)
“問題導學”是高中數學中的一個重要教學模式,它強調了各個教學階段中對數學問題的合理運用,進而達到更為理想的教學效果.作者從相關理論出發,從實踐經驗中總結出了一些典型方法,在文中進行了細致闡述.
高中;數學;問題導學
在高中數學教學過程當中,無論從語言上還是從文字上,都會十分頻繁地運用到提問的方式.在很多師生看來,這已經是一個習以為常的行為了,根本沒有意識到其中具有哪些更加深層次的教學意義.其實,只要停下來認真思索便會發現,不同的問題形式和內容,能夠觸發的教學效果都是不一樣的.讓問題運用成為一種條理化的教學模式,將可以為高中數學教學提供新的思路.
一、以問題激興趣,增加學生學習熱情
想要在高效率之下開展學習,必須要對學習過程具有興趣和熱情.這個道理在高中數學教學當中也同樣適用.其實,想要激發起學生們的學習興趣并不困難,很多時候只需要一個巧妙的設問,便可以將大家的熱情觸發出來,讓接下來的教學活動進展得順暢高效.
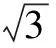
為了能夠切實增加學生們對于數學知識的探究熱情,教師們可以運用一些難度不大,但趣味性較強的問題.這時加入問題的目的并不在于深化知識理解,而是要將學生們的思維打開,引導到數學思考的路徑上來.
二、以問題延思維,合理搭建思維階梯
數學知識的學習是一個不斷深入的過程.而這個過程也并不是一蹴而就的.如果直接把問題的難度提升上去,非但不能優化學生們的思考效果,反而會讓大家難以接受,進而產生對數學學習的抵觸情緒.如何能夠運用巧妙的問題設計,引領學生們的思維在適當的速率下實現深化呢?這就是教師們需要研究的設計方法了.
例如,為了逐步深化學生們對于函數知識的理解,我向大家提出了這樣一個問題:已知,a、b均為實數,且函數f(x)=x3+ax2+bx的兩個極值點分別是1和-1,則(1)a和b的值分別是什么?(2)若函數g(x)的導函數g′(x)=f(x)+2,那么,函數g(x)的單調區間是什么?(3)已知函數h(x)=f(f(x))-c,且c∈[-2,2],那么,函數y=h(x)有多少個零點?很明顯,隨著上述三個問題的逐個出現,很自然地將學生們的思維由表面引向了深入.以提問的方式對學生們的思維進行延展,效果遠比教師的語言敘述要理想得多.多為學生們提供一些這樣的階梯式問題,也是在潛移默化中向學生明確,數學學習需靈活思考,不斷深入,思考是沒有盡頭的.
為了實現學生數學思維的逐步深化,教師們往往需要設置多個問題,讓每個問題之間拉開難度梯度,在無形中為學生們建立起一個思維引導方向.隨著這樣的問題思考,學生們很自然地走向了數學知識的深處,整個探究過程自然順暢.
三、以問題找方法,透過不同尋找相同
數學問題在高中階段教學當中的作用并不僅僅是引發學生們的思考,還可以啟發大家從更高的視角來發現數學學習當中的規律與方法.這也對教師們設計問題的思路與能力提出了比較高的要求.
例如,為了引導學生們理解并提煉出方程的思想方法,我在課堂上為學生們設計了如下兩道練習題:(1)已知數列{an}是一個公差不為零的等差數列,它的前n項和是Sn.如果a3和a7的等比中項是a4,且S8的值是32,那么,S10的值是多少?(2)已知,拋物線y2=2px(p>0)的焦點是點F,過該點作一條傾斜角是45°的直線,分別與拋物線相交于點A和點B.如果線段AB的長度是8,那么p的值是多少?這兩道題目,表面看來分別屬于不同的內容范疇,但經過具體解答,學生們發現,二者的分析方法之間是存在著些許相似的.在第一個問題中,根據“a3和a7的等比中項是a4”和“S8的值是32”兩個條件可以分別列出兩個方程,將之聯立為方程組便可以分別求出a1和d的值.而在第二個問題中,則是將A、B兩點的坐標分別設為A(x1,y1)和B(x2,y2),將過焦點的直線方程設為y=x

通過將教學問題進行科學的處理,“問題導學”教學模式的路徑已經清晰地展現出來了.通過對數學問題的巧妙運用,學生們收獲了從學習心態到學習方法的提升.從教學的尋常之處入手,將每一次提問都進行高質量的優化,便可以在不增加任何教學成本的前提下實現教學實效的全面提升.這種“問題導學”的教學模式,值得廣大高中數學教師們進行更加細致深入的探索.
[1]章建華. 分類討論思想在高中數學解題中的應用[J]. 新課程(下),2015(09).
[2]倪小紅. 讓數學思想潤“物”細無聲[J]. 數理化解題研究,2015(11).
[責任編輯:楊惠民]
2017-05-01
李帶兵(1981.9-),男,江蘇連云港人,中小學一級教師,本科學歷,主要從事高中數學教學與研究.
G632
B
1008-0333(2017)18-0043-02

