基于改進遺傳算法的汽車傳動系統扭轉振動優化與仿真

吳 浩,王 芳

(1.武漢軟件工程職業學院 汽車工程學院,武漢430205; 2.武漢紡織大學 機械工程與自動化學院,武漢430073)

?

基于改進遺傳算法的汽車傳動系統扭轉振動優化與仿真

吳 浩1,王 芳2

(1.武漢軟件工程職業學院 汽車工程學院,武漢430205; 2.武漢紡織大學 機械工程與自動化學院,武漢430073)

當前,汽車傳動系統扭轉振動比較嚴重,導致車輛產生很大的噪音現象.對此,采用改進遺傳算法對車輛傳動系統參數進行優化,并對優化結果進行仿真驗證.創建了汽車傳動系統運動模型簡圖,推導出傳動系統運動控制方程式,采用分布-集中建模方法求解角速度的響應率.構造優化目標函數,采用改進遺傳算法對車輛傳動系統參數進行優化.建立車輛傳動系統扭轉仿真模型,采用Matlab/Simulink軟件對優化后的參數進行仿真.同時,與優化前進行對比和分析.仿真結果顯示:采用改進遺傳算法優化后,變速器和差速器的角速度峰值分別降低了25.8%和31.1%,變速器和差速器的角加速度峰值分別降低了23.1%和25.6%.采用改進遺傳算法優化車輛傳動系統參數,可以減少傳動系統扭轉振動幅度,降低車輛噪音.

汽車傳動系統; 扭轉振動; 改進遺傳算法; 優化; 仿真

當前,人們對汽車的輕量化和燃油消耗進行了廣泛研究,從而提高整車的綜合性能[1].然而,這些性能改善的同時也可能導致車輛產生振動噪聲.其中與振動噪聲有關的重要系統就是車輛傳動系統.傳動系統的噪聲主要是由于齒輪傳動發出的聲響.車輛怠速發出的咔噠聲是因低負荷下齒輪運動摩擦引起的.因為傳動系統部件轉動慣量和阻尼系數較小,所以在飛輪添加扭矩時容易引起振動噪聲現象.傳動系統的扭轉振動是車輛振動形式之一,也是整車性能評價的重要因素[2].扭轉振動產生的噪聲不僅影響乘坐的舒適性,而且還有可能導致車輛傳動動力的中斷.因此,建立車輛傳動系統模型,研究車輛扭轉振動現象,降低車輛扭轉振動噪音具有重要的意義.

為了降低車輛扭轉振動現象,研究人員從不同方向對車輛傳動系統展開了研究.文獻[3-4]選取某一車型,構造汽車傳動系統扭轉力學模型,研究汽車傳動系統摩擦離合器減震器的扭轉性質,優化了減震器的參數,建立了整車的動力傳動系統仿真模型,對車輛減震性能進行了仿真和分析.減小了扭轉振動幅度,降低傳動系統力矩的波動,提高汽車行駛的平穩性.文獻[5-6]研究了汽車傳動系統雙質量飛輪參數的優化設計方法,構造了雙質量飛輪設計模型,推導出飛輪轉動慣量、扭轉剛度與振動頻率的關系式.根據減震原理,創建多級扭轉剛度的優化目標,通過實驗驗證設計模型的正確性,從而降低發動機旋轉的振動幅度.文獻[7-8]建立了傳動系統扭轉振動有限元模型,采用有限元軟件對扭轉振動進行有限元分析,計算扭轉振動的共振頻率.通過優化傳動軸當量夾角,從而減低車輛扭轉振動的頻率.以往研究傳動系統的扭轉振動幅度得到了改善,但是振動峰值較大,從而影響車輛行駛的平穩性.對此,本文采用了改進遺傳算法對汽車傳動系統扭轉振動進行優化.創建了汽車傳動系統運動模型簡圖,給出了傳動系統傳動控制方程式.采取改進遺傳算法對參數進行優化,建立仿真模型,將優化結果導入到Matlab/Simulink仿真模型中進行驗證.同時,與優化前仿真結果進行對比,改進遺傳算法優化后的傳動系統,變速器和差速器角速度、角加速度峰值明顯降低.車輛傳動系統的扭轉振動幅度較小,降低了傳動系統的噪音,提高了車輛行駛的穩定性.

1 汽車動力傳動系統

本文研究的是發動機飛輪前置、后輪驅動汽車行駛的動力傳動系統,如圖1所示.采用分布-集中建模技術處理運動方程的求解問題.

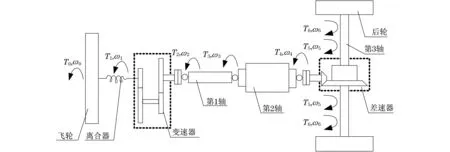
圖1 汽車動力傳動系統

1.1 分布式構件

第1根驅動軸角速度與外加力矩在頻域內的數量關系為

(1)

第2根驅動軸角速度與外加力矩在頻域內的數量關系為

(2)

第3根分布式半軸角速度與外加力矩在頻域內的數量關系為

(3)

(4)

式中:Ej為頻率變換變量;Tjs為傳播時間延遲;ξj為特性阻抗;li為軸的長度;Jj為轉動慣量;Gj為剪切模量;ρj為密度;i=1,2,3;j=1,2,3.

1.2 集中式構件

由拉格朗日動力學方程式可知,車輛傳動系統相關部件扭轉控制方程[10-11]如下:

飛輪控制方程式為

T0(iω)-T1(iω)=ω0(iω)(iJfω+Bf)

(5)

離合器控制方程式為

(6)

變速箱控制方程式為

(7)

(8)

(9)

差速箱控制方程式為

(10)

(11)

車輪總成控制方程式為

(12)

式中:T0為輸入轉矩;Ti為傳遞力矩,i=1,2,…,6;ω為頻率;ωi為角速度,i=0,1,…,6;Jf,Jg,Jd,Jw為轉動慣量;Bf,Cc,Bg,Bd,Bw為阻尼系數;kc為扭轉剛度;ng=ω1/ω2;nd=ω4/ω5.

因為整體模型一共分為3個分布式參數段及5個總成集中式參數段,利用式(1)～(3),(5)～(7),(9)～(11),車輛動力傳動系統完整的分布-集中(復合)整體模型可用如下矩陣形式表示:

(13)

求解式(13),可得ω0,ω1,ω3,ω4和ω6響應率分別為

式中:

2 傳動系統參數優化

2.1 改進遺傳算法

遺傳算法[12]是一種新型的機器學習方法,它基于達爾文提出的物種進化論中的自然選擇定則并對其進行模擬仿真,通過仿真采用的算法處理所得信息,并以此為基礎進行自然選擇的過程.遺傳算法將自然選擇論巧妙地適用到了人工篩選處理信息的工作范疇之中.在工程領域中,遺傳算法雖然能夠搜索到全局的最優值,但是種群迭代次數太多,搜索速度較慢.對此,本文采用改進遺傳算法.改進遺傳算法是在遺傳算法的基礎上采取實數編碼機制對交叉算子、變異算子及選擇算子進行改進.

交叉算子的計算公式[13]如下:

(15)

變異算子的計算公式[13]如下:

(16)

式中:μ為[0,1]之間的隨機數;N為進化的當前代數;N*為進化的最大代數;(α,β)為上代染色體;(α*,β*)為下代染色體.

選擇算子的改進方法如下:① 將交叉和變異生成下代染色體、上代染色體進行重新組合成新的種群;② 對新的種群進行重新排列;③ 刪去種群中重復的染色體;④ 按照順序選擇兩個染色體,計算其概率,當概率大于[0,1]時,上一個染色體選入新的種群,否則,下一個染色體選入新的種群.

2.2 優化目標函數

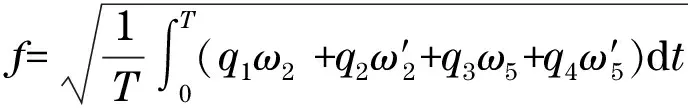
(17)

式中:q1,q2,q3和q4為加權系數;ω2和ω5分別為變速器和差速箱的角速度;ω′2和ω′5分別為變速箱和差速箱的角加速度.

改進遺傳算法種群大小為50,隨機數ω=0.95,ω1=0.5,變異概率為0.01,交叉概率為0.98,最大進化代數為200.采用改進遺傳算法的迭代曲線如圖2所示.

圖2 改進遺傳算法適應度收斂曲線

由圖2可知,遺傳算法和改進遺傳算法都能向最優解逼近,但是改進遺傳算法不僅收斂速度更快,而且收斂時取得極小值更小.因此,改進遺傳算法求解優于遺傳算法.采用改進遺傳算法優化的結果如表1所示.

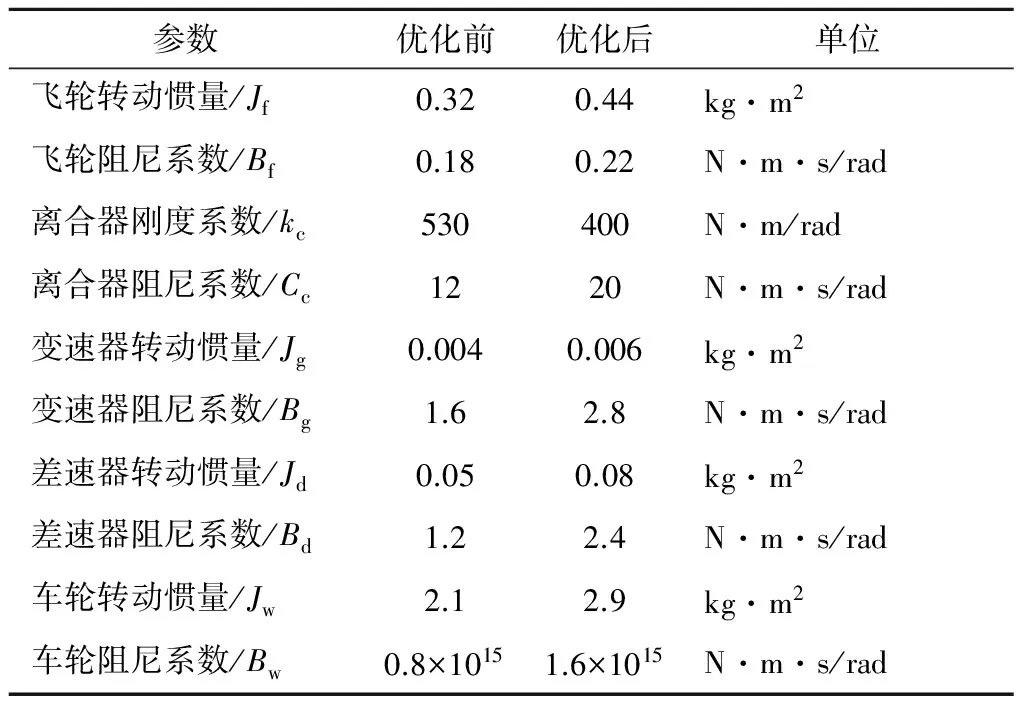
表1 傳動系統優化參數

3 仿真及分析

本文研究的主要目的是利用分布-集中(復合)建模技術分析車輛動力傳動系統的扭轉振動現象,從而減少車輛傳動的噪音.運用Matlab/Simulink工具箱軟件建立了車輛動力傳動系統的仿真模型,仿真模型如圖3所示.仿真參數如下:飛輪轉矩T0=150 N·m,脈沖持續時間t1=40 ms,變速器的齒輪傳動比ng=2.1,差速器的齒輪傳動比nd=4.1,第1根軸轉動慣量J1=1.55 kg·m2,第1根軸的長度l1=0.53,第2根軸轉動慣量J2=1.22 kg·m2,第2根軸的長度l1= 0.95,第3根軸轉動慣量J3=7.68 kg·m2,第2根軸的長度l3=0.78,剪切模量G1=G2=8.5×108N/m2,G3=7.2 ×108N/m2,車輪密度ρ=7 810 kg/m3,仿真時間t=2 s其他仿真參數如表1所示.變速器和差速器的角速度分別如圖4和圖5所示.變速器和差速器的角加速度分別如圖6和圖7所示.

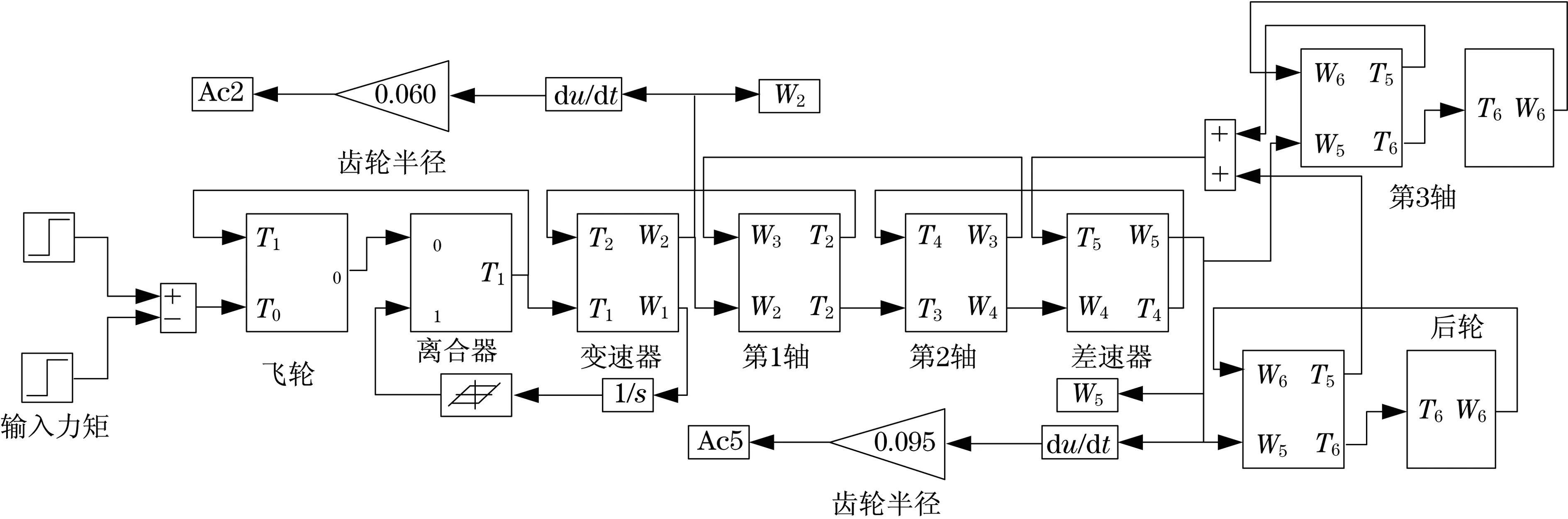
圖3 車輛動力傳動系統仿真模型

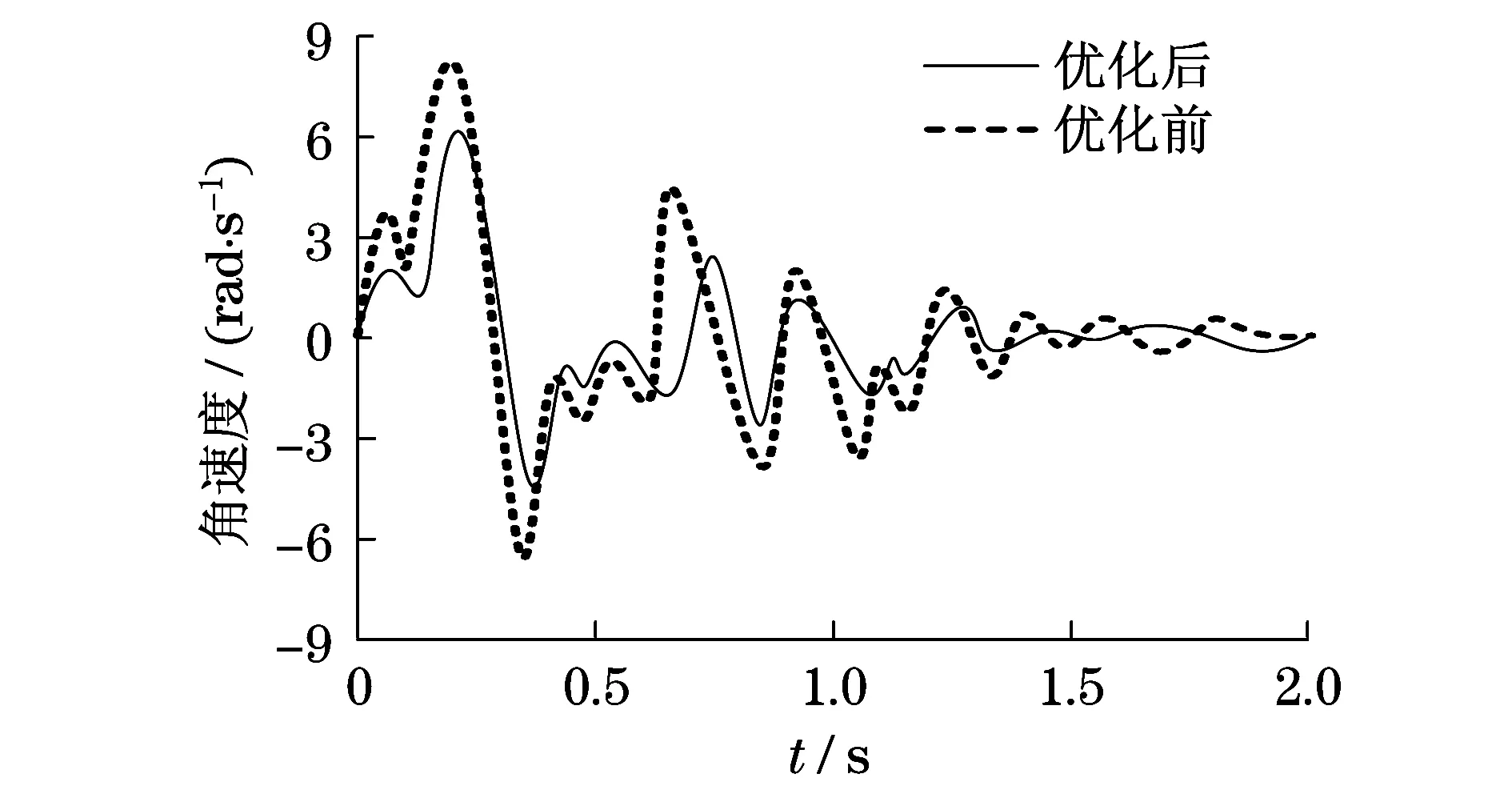
圖4 變速器角速度變化曲線

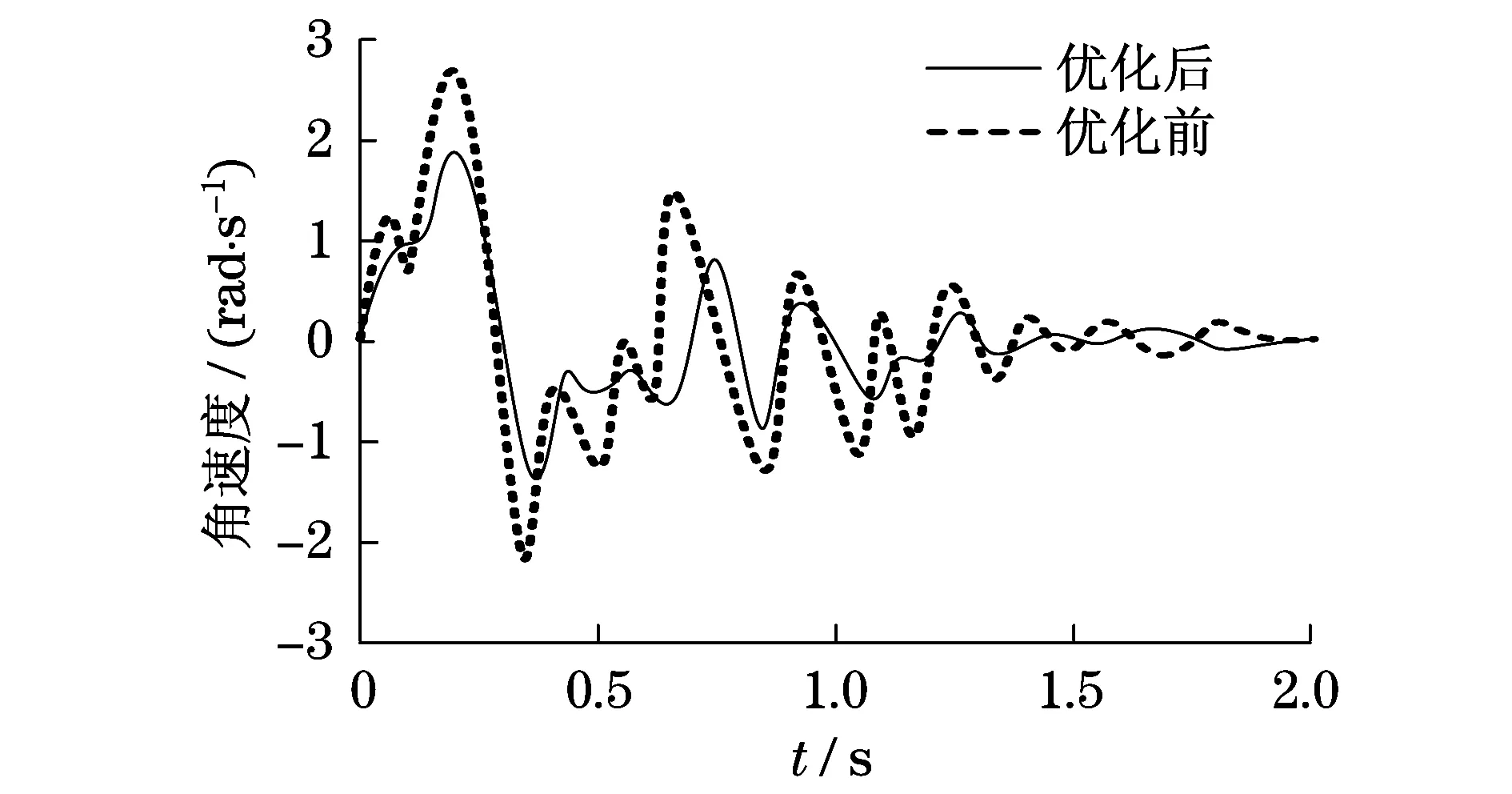
圖5 差速器角速度變化曲線

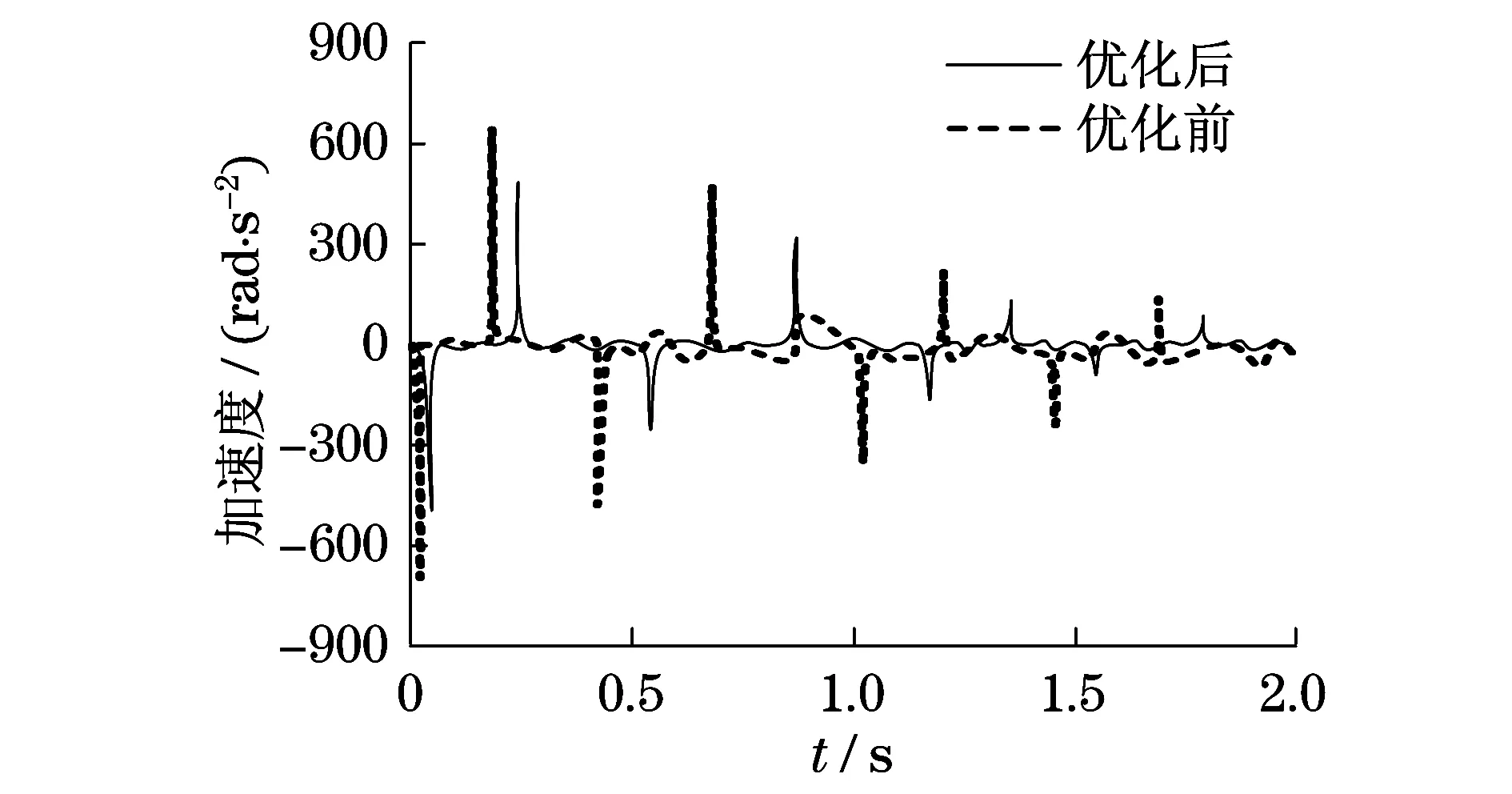
圖6 變速器角加速度變化曲線

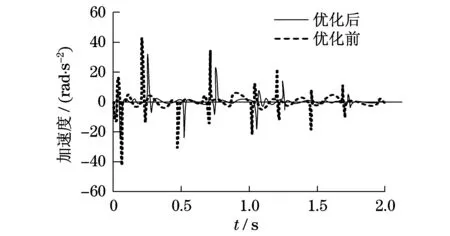
圖7 差速器角加速度變化曲線

由圖4和圖5可知,變速器和差速器的角速度優化前峰值分別為8.25 rad/s和2.73 rad/s,而采用改進遺傳算法優化后,變速器和差速器的角速度峰值分別為6.12 rad/s和1.88 rad/s,采用改進遺傳算法優化后變速器和差速器的角速度峰值分別降低了25.8%和31.1%.由圖6和圖7可知,變速器和差速器的角加速度優化前峰值分別為650 rad/s2和43 rad/s2,而采用改進遺傳算法優化后,變速器和差速器的角加速度峰值分別為500 rad/s2和32 rad/s2,采用改進遺傳算法優化后變速器和差速器的角速度峰值分別降低了23.1%和25.6%.同時,變速器和差速器的角速度、角加速度變化幅度較小.因此,變速器和差速器采用改進遺傳算法優化后,降低了傳動系統的振動噪音.

5 結語

本文建立了汽車傳動系統模型,給出了傳動系統的分布-集中控制方程式.對傳動系統變速器和差速器的角速度進行了推導.采用改進遺傳算法對變速器和差速器的角速度和角加速度進行了優化.構造了傳動系統的仿真模型,對優化后的變速器和差速器的角速度和角加速度變化曲線進行仿真驗證.同時,與優化前進行了對比和分析.采用改進遺傳算法優化后的變速器和差速器角速度和角加速度不僅峰值降低,而且整體振動幅度也有所降低,這為降低傳動系統的振動噪音研究提供了參考依據.

[1]] 朱磊.基于超級電容的并聯式混合動力轎車動力總成系統開發與試驗研究[D].鎮江:江蘇大學,2009.

ZHU Lei.The powertrain system development and experiment research of parallel hybrid electric vehicle with ultra capacitor[D].Zhenjiang:Jiangsu University,2009.

[2] 郭亞敏.雙質量飛輪扭轉減振器非線性結構和特性的研究[D].太原:太原理工大學,2015.

GUO Yamin.The structure and nonlinear characteristic study of dual mass flywheel[D].Taiyuan:Taiyuan University of Technology,2015.

[3] 丁原.汽車摩擦離合器扭振減振器特性研究與參數分析[D].長春:長春理工大學,2009.

DING Yuan.Automotive friction clutch torsional vibration damper characteristics and parametric analysis[D].Changchun:Changchun University of Science and Technology,2009.

[4] 劉強.基于發動機激勵的汽車起步離合器接合的動力傳動系統扭轉振動研究[D].西安:長安大學,2015.

LIU Qiang.Study on torsional vibration of vehicle transmission system of starting clutch engagement based on engine excitation[D].Xi’an:Chang’an University,2015.

[5] 陳雷.雙質量飛輪性能參數優化設計方法[J].內燃機學報,2012,30(3):278-283.

CHEN Lei.Optimization method of performance parameters of dual mass flywheel[J].Transactions of CSICE,2012,30(3):278-283.

[6] 嚴正峰.雙質量飛輪設計與制造的關鍵技術研究[D].武漢:武漢理工大學,2009.

YAN Zhengfeng.Research on the key technology of dual mass flywheel design and manufacturing[D].Wuhan:Wuhan University of Technology,2009.

[7] 陳宏強.汽車動力傳動系扭振分析與仿真優化[D].長沙：湖南大學,2012.

CHEN Hongqiang.Vehicle powertrain torsional analysis and simulation improvement[D].Changsha:Hunan University,2012.

[8] 張玉倫.多軸驅動汽車動力傳動系統扭振固有特性及其隨機性分析[D].長春:吉林大學,2015.

ZHANG Yulun.Analysis of the natural torsional vibration characteristics and its randomness for the powertrain of multi-axle driving automobile[D].Changchun:Jilin University,2015.

[9] MATSUMOTO S.Nonlinear identification of torsional driveshaft vibrations in a full-scale automotive vehicle during acceleration[J].Nonlinear Dyn,2016,86(2):712-720.

[10] 許在文,萬海橋,黃東東,等.汽車傳動系扭轉振動建模與仿真分析[J].合肥工業大學學報,2012,35(1):13-16.

XU Zaiwen,WAN Haiqiao,HUANG Dongdong,et al.Modeling and simulation analysis of vehicle transmission torsional vibration[J].Journal of Hefei University of Technology,2012,35(1):13-16.

[11] WALKER P D,ZHANG N.Active damping of transient vibration in dual clutch transmission equipped power-trains:a comparison of conventional and hybrid electric vehicles[J].Mechanism and Machine Theory,2014,77(2):2-10.

[12] KANARACHOS S.Intelligent road adaptive suspension system design using an experts’ based hybrid genetic algorithm[J].Expert Systems with Applications,2015,42(21):8232 -8242.

[13] FU S P,LI S B,LUO N,et al.Dynamic optimization of tracked vehicle power train based on torsional vibration analysis[J].Advances in Mechanical Engineering,2016,8(5):589-597.

Optimization and simulation of torsional vibration of vehicle transmission system based on improved genetic algorithm

WU Hao1,WANG Fang2

(1.School of Electronic Engineering,Wuhan Vocational College of Software and Engineering,Wuhan 430205,China;2.Mechanical Engineering and Automation College,Wuhan Textile University,Wuhan 430073,China)

At present,the automobile transmission system torsional vibration is quite serious,causes the vehicle to have the very big noise phenomenon.In this paper,an improved genetic algorithm is used to optimize the parameters of vehicle transmission system,and the simulation results are validated.The kinematic model of the transmission system is created,and the motion control equation of the transmission system is deduced.The response rate of the angular velocity is solved by the distributed-centralized modeling method.The optimization objective function is constructed,and the parameters of vehicle transmission system are optimized by improved genetic algorithm.The simulation model of the vehicle transmission system is established,and the optimized parameters are simulated by Matlab/Simulink.At the same time,compared with the pre-optimization and analysis.The simulation results show that the angular velocity of the transmission and the differential are reduced by 25.8% and 31.1% respectively,and the angular acceleration of the transmission and the differential are reduced by 23.1% and 25.6% respectively by using the improved genetic algorithm.Using the improved genetic algorithm to optimize the parameters of vehicle transmission system can reduce the torsional vibration amplitude of the transmission system and reduce the vehicle noise.

automobile transmission system; torsional vibration; improved genetic algorithm; optimization; simulation

湖北省自然科學基金資助項目(2012CFB092)

吳 浩(1980—),男,講師.E-mail:haow201611@126.com

U 463

A

1672-5581(2017)02-0141-06