中國東部各省市區域創新能力評價

徐永智，衣保中

(1.吉林大學 東北亞研究院，長春 130012；2.黑龍江科技大學 經濟學院，哈爾濱 150028)

?

·經濟理論與實踐探索·

中國東部各省市區域創新能力評價

徐永智1,2，衣保中1

(1.吉林大學 東北亞研究院，長春 130012；2.黑龍江科技大學 經濟學院，哈爾濱 150028)

區域創新指標體系的建立是綜合評價區域創新能力的基礎,區域創新能力指標體系不僅包括知識能力，也包括區域創新環境。基于對主成分分析的不足，通過均值化和對數中心化處理改進主成分分析的特征提取，并用熵值法對主成分的綜合值計算進行改進，再用改進后的主成分方法對中國東部各省市區域創新能力進行綜合評價，可以看出，知識能力的特征向量都為負值，而創新環境都為正值，這意味著作為區域創新潛力的區域創新環境對一個區域的創新能力有正向作用，而知識能力只表現為當前的知識投入與產出。

區域創新能力；均值化；對數中心化；熵值法

1992年，Cooke首次提出區域創新體系概對應念，該概念與1987年Freeman等人提出的國家創新體系概念相對應[1]。自區域創新概念提出后，學者們對區域創新模式、區域創新系統等理論進行了深入研究，與此同時定量研究也受到了廣泛關注，其中對區域創新能力的實證研究是一個熱點與重點，而區域創新指標體系的建立是對區域創新能力做出評價的基礎。

用單一指標，比如專利數、發表論文數等衡量區域創新能力，顯然有失偏頗，因此對區域創新能力的評價更多的是建立在多元指標體系上。王稼瓊、繩麗惠、陳鵬飛(1999)認為，區域創新體系以技術創新為主，企業是技術創新的主體[2]。甄峰、黃朝永、羅守貴(2000)從知識創新能力、技術創新能力、管理與制度創新、宏觀經濟與社會環境四個方面建立了指標體系[3]。《2003中國區域創新能力報告》認為，區域創新能力是指一個地區將知識轉化成新產品、新工藝、新服務的能力，該報告中的指標體系由以下五個要素構成：知識創造能力、知識獲取能力、企業的技術創新能力、創新環境和創新經濟績效[4]。丁美霞、周民良(2008)在對中國各省區的區域創新能力的分析中，將區域創新能力分為四個方面：創新投入、創新產出、創新配置和創新環境[5]。侯風華、趙國杰(2008)在建立中國東部省市區域創新能力指標時，將區域創新能力分成當前與長遠創新能力，其中，當前或短期的創新能力用短期的區域創新技術能力代表，而長遠或潛在的創新能力則用區域創新因素反映[6]。可見，區域創新不是科技能力，也不是地區科技競爭力[7]。結合前面的文獻，我們認為，區域創新能力不僅僅是知識能力[8]，也包括了區域創新環境，這與侯風華、趙國杰(2008)給出的兩個階段較為一致。

對區域創新能力的多元指標進行綜合評價，文獻中出現了如下方法：主成分分析(PCA)、核主成分分析(KPCA)、層次分析法(AHP)、聚類分析、因子分析、數據包絡分析(DEA)、集對分析法(SPA)。在這些評價方法中，雖然主成分分析被應用最多，但傳統的主成分分析局限于指標間具有很強的線性關系，而且傳統的正態標準化沒有包含原數據的所有信息。盡管KPCA是建立在指標間非線性關系上的，相較于主成分分析有更強的特征提取能力，但缺點是對提取的特征不能做出很好的現實解釋。另外，PCA在最后綜合評價值的計算上，通常取各主成分的方差貢獻率作為權重，這帶有很強的主觀性。針對上述不足，我們借鑒了侯風華、趙國杰(2008)的指標體系，一方面通過均值化和非線性主成分分析改進了主成分分析的特征提取，另一方面用熵值法對主成分的綜合得分進行了改進。

一、區域創新能力的評價方法

1.主成分特征提取的兩點改進

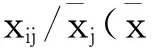
其次，我們改進了PCA僅適于線性分析的不足。主成分分析適用于指標間線性相關性很強的情形，但有時通過主成分分析后發現主成分特征值相差不大，累積貢獻率比較小，這時就可以嘗試用非線性主成分分析。另外，非線性主成分也可以作為PCA的一個補充，即在進行PCA時，不妨同時進行對數中心化主成分分析。設有一個n行p列的矩陣，其中n為樣本總個數，p為指標項數，則對數中心化步驟如下[10]：

先對原始數據xij進行對數變換，以及行向量中心化：

(1)

然后從協方差矩陣出發，計算Z的協方差矩陣及其特征值與特征向量，根據累計貢獻率大于85%選擇m個(m

(2)

2.主成分綜合值計算的改進

第一，計算第j項指標下第i個樣本的比重：

(3)

第二，計算第j項指標的熵值：

(4)

第三，計算第j項指標的權重：

(5)

第四，計算第i個樣本的綜合值

(6)

在第一步中，為防止矩陣中有數據為負，可以將所有數據加上一個最小負數的絕對值，這種平移處理不會改變結果。然后按照平移后的矩陣進行第二到第六步的計算。

二、區域創新能力綜合評價

我們在第一部分得出，區域創新能力包括知識能力，也包括區域創新環境，其指標數據見參考文獻[6]。我們依照第一部分的三點改進，分別計算了均值化后的主成分、對數中心化的主成分，以及在最后用熵值法對前面求的主成分矩陣進行綜合計算。

表1 三種主成分的前三個特征值、貢獻率及累計貢獻率

表2 對數中心化主成分的特征向量

表3 平移后的主成分得分以及權重

首先，我們對比了三種主成分的特征提取能力，如下表1所示，三者特征提取能力相差很少，前三個特征值的累計貢獻率都達到了90%以上。在表2中，我們給出了三個主成分的特征向量，由此可以確定三個主成分方程。相比而言，對數中心化具有較好的累計貢獻率，所以我們選擇對數中心化的主成分進行下一步的綜合計算。通過計算，提取的三個主成分最小值為-12.23，因此為使矩陣沒有負值，可以平移13個單位。我們在表3中給出了平移后的主成分以及用熵值法計算后的三個主成分的權重(在括號中)。我們在表4中給出了用表3的權重計算的綜合得分，并對比了用表1的貢獻率作為主成分權重所計算出的結果，以及對比了文獻[6]給出的綜合評價結果。

表4 三種綜合評價結果的對比

由表3可以看出，第一主成分的權重達到了84.16%，而第二主成分與第三主成分分別為10.27%、5.57%，這與表1中的三個貢獻率作為權重有很大不同。但本文中的權重是基于熵值法算出的，因此具有客觀性。由于權重的不同，表4中的排序也出現很大的不同，如第一、第二名，廣東與江蘇分別代替了上海、北京，特別是廣東排序變化最大。從表3中可以看出，由于第一主成分中廣東與江蘇主成分得分居前，而權重又占了84.16%，因此盡管它們在第二、第三主成分的得分低于上海、北京，但在綜合評價中還是占有優勢。我們從表2中的知識能力與創新環境的特征向量可以看出，知識能力的特征向量都為負值，而創新環境都為正值，可以看出作為區域創新潛力的區域創新環境對一個區域的創新能力有正向作用，而知識能力只表現為當前的知識投入與產出，因此第一主成分很好地綜合了兩個階段的區域創新能力，在權重上也占據主導。文獻[6]的因子分析結果，與非線性PCA-熵值法的差別較大，與非線性PCA差別較小，反映了因子分析在綜合計算中的主觀性，另外值得一提的是，通常在因子分析中，樣本個數是指標個數的5倍，文獻[6]用因子分析是值得商榷的。

首先，本文在前人的研究基礎上，總結出區域創新能力指標體系不僅包括知識能力，也包括區域創新環境；其次，我們針對目前主成分分析的不足，一方面通過均值化和非線性主成分分析改進了主成分分析的特征提取，另一方面用熵值法對主成分的綜合值計算進行了改進；最后，我們借鑒文獻[6]的指標體系進行了對比實證研究，得出對數中心化主成分與熵值法的結合能更客觀更準確地應用于區域創新能力的綜合評價中。

[1] Freeman C.Technology Policy and Economic Performance:Lessons from Japan[M].London: Pinte,1987.

[2] 王稼瓊,繩麗惠,陳鵬飛. 區域創新體系的功能與特征分析[J].中國軟科學,1999，(2):53-55.

[3] 甄峰,黃朝永,羅守貴.區域創新能力評價指標體系研究[J].科學管理研究,2000，(6):5-8.

[4] 中國科技發展戰略小組.2003中國區域創新能力報告[M].北京：經濟管理出版社,2004：20-22.

[5] 丁美霞,周民良.中國各省區創新能力的動態趨勢與影響因素分析[J].經濟學家,2008，(1):63-65.

[6] 侯風華，趙國杰.我國東部省市的區域創新能力評價研究[J].科學管理研究, 2008，(2):21-23.

[7] 柳卸林,胡志堅.中國區域創新能力的分布與成因[J].科學學研究,2002，(5):550-555.

[8] 胡鞍鋼,熊義志.我國知識發展的地區差距分析：特點、成因及對策[J].管理世界,2000，(3):5-10.

[9] 葉雙峰. 關于主成分分析做綜合評價的改進[J].數理統計統計與管理,2001，(2):52-55.

[10] 陳述云,張崇甫.對多指標綜合評價的主成分分析方法的改進[J].統計研究,1995，(1):35-39.

[11] 郭顯光.改進的熵值法及其在經濟效益評價中的應用[J].系統工程理論與實踐,1998，(12)：98-102.

[責任編輯：陳淑華]

2016-10-12

黑龍江省社會科學基金項目“黑龍江省資源型城市轉型的創新模式研究”(14B079)

徐永智(1965—)，女，教授，經濟學博士，從事區域經濟研究；衣保中(1963—)，男，吉林長春人，教授，博士生導師，從事區域經濟研究。

F121

A

1007-4937(2017)01-0082-04