相位型三頭薛定諤貓態(tài)的量子統(tǒng)計(jì)屬性?

林惇慶 朱澤群 王祖儉 徐學(xué)翔2)?

1)(江西師范大學(xué)物理與通信電子學(xué)院,南昌 330022)

2)(江西師范大學(xué),量子科學(xué)與技術(shù)中心,南昌 330022)

相位型三頭薛定諤貓態(tài)的量子統(tǒng)計(jì)屬性?

林惇慶1)朱澤群1)王祖儉1)徐學(xué)翔1)2)?

1)(江西師范大學(xué)物理與通信電子學(xué)院,南昌 330022)

2)(江西師范大學(xué),量子科學(xué)與技術(shù)中心,南昌 330022)

(2016年12月25日收到;2017年3月8日收到修改稿)

本文詳細(xì)研究了一種相位型三頭薛定諤貓態(tài)的一些量子統(tǒng)計(jì)屬性,包括光子數(shù)分布、平均光子數(shù)、亞泊松分布、壓縮效應(yīng)以及Wigner函數(shù)等.我們發(fā)現(xiàn),三頭貓態(tài)的Wigner函數(shù)都可以出現(xiàn)負(fù)值,與二、四頭貓態(tài)一樣,說(shuō)明它們都可以體現(xiàn)出非經(jīng)典特性.與二頭貓態(tài)不同,三頭貓態(tài)在一定參數(shù)范圍內(nèi)可以呈現(xiàn)亞泊松分布,這點(diǎn)與四頭貓態(tài)相類似,但弱于四頭貓態(tài).另外,三頭貓態(tài)和四頭貓態(tài)都沒(méi)有壓縮屬性,但二頭貓態(tài)具有壓縮屬性.

∶薛定諤貓態(tài),三頭貓態(tài),非經(jīng)典性,Wigner函數(shù)

PACS∶42.50.Dv,03.65.—wDOI∶10.7498/aps.66.104201

1 引 言

在量子力學(xué)中,態(tài)疊加原理是一個(gè)最基本的原理,也是量子態(tài)的不同表象的理論基礎(chǔ)[1,2].理論上可以將一些已有的或成熟的量子態(tài)通過(guò)疊加,構(gòu)造出不同類型的新量子態(tài),以滿足工程和技術(shù)的需要[3?5].國(guó)內(nèi)外科研人員對(duì)量子態(tài)疊加開展了大量的理論和實(shí)驗(yàn)的研究,特別是近幾十年來(lái),薛定諤貓態(tài)引起了人們的廣泛關(guān)注和極大興趣.因?yàn)檠Χㄖ@貓態(tài)光場(chǎng),就是指由若干個(gè)截然不同的、并且在宏觀上完全可以分辨的量子光場(chǎng)態(tài)的線性疊加所組成的新的疊加態(tài)光場(chǎng)[6].

根據(jù)所參與疊加的量子態(tài)的幅度和相位的不同,可將薛定諤貓態(tài)分為幅度型薛定諤貓態(tài)(光場(chǎng))、相位型薛定諤貓態(tài)(光場(chǎng))以及幅度-相位混合型薛定諤貓態(tài)(光場(chǎng)).同時(shí),根據(jù)所參與疊加的量子態(tài)的數(shù)目多少,可將薛定諤貓態(tài)區(qū)分為多少頭貓態(tài).眾所周知,相干態(tài)是量子光學(xué)領(lǐng)域中的一種典型量子態(tài)[7].疊加不同相干態(tài),已經(jīng)成為研究大量基本問(wèn)題(如宏觀疊加態(tài)的退相干)的重要工具.比如,最早“貓態(tài)”(2HCS)的概念,來(lái)自量子力學(xué)的奠基人之一薛定諤在1935年提出的一個(gè)著名的“佯謬”,即箱子里面的一只貓不是死的也不是活的,而是同時(shí)處于死和活的狀態(tài).這種薛定諤貓態(tài)可由兩個(gè)相位相差π的相干態(tài)疊加而成,即我們可以稱之為相位型的二頭貓態(tài),這種量子態(tài)在量子信息技術(shù)中得到了廣泛應(yīng)用[8].

近幾年,有些研究已將這種量子疊加延伸到包含更多數(shù)目的相干態(tài)疊加.實(shí)際上,“薛定諤貓態(tài)”在宏觀世界是不存在的,然而在微觀世界科學(xué)家們可以用光子或者原子來(lái)制備這些“貓態(tài)”.Yukawa等[9]提出了一種實(shí)驗(yàn)方案,成功地產(chǎn)生了三種光子數(shù)態(tài)的疊加,同時(shí)也考慮了兩種和三種不同相位的相干態(tài)的疊加情況.Vlastakis等[10]利用腔腸電動(dòng)力學(xué)成功實(shí)現(xiàn)了由高達(dá)四種不同相位的相干態(tài)的疊加而成的量子態(tài).再比如,Raimonnd等[11]制備了形如的量子態(tài).

實(shí)際上,不同的疊加量子態(tài)表現(xiàn)出不同的干涉性和非經(jīng)典性.最近,Lee等[12]研究了由四種不同相干態(tài)疊加而成的四頭貓態(tài)并應(yīng)用于進(jìn)行量子相位估計(jì).他們展示了該量子態(tài)的非經(jīng)典性特點(diǎn),可以提高相位估計(jì)的分辨率.然而,對(duì)于三頭貓態(tài)的研究,盡管有文獻(xiàn)提及甚至實(shí)驗(yàn)實(shí)現(xiàn),但都沒(méi)給出詳細(xì)的理論研究.基于這些原因,我們擬對(duì)一種相位型三頭貓態(tài)的量子統(tǒng)計(jì)屬性進(jìn)行詳細(xì)的理論研究,并與相干態(tài)、二頭貓態(tài)和四頭貓態(tài)進(jìn)行對(duì)比分析.

本文首先定義描述三頭貓態(tài)光場(chǎng)的量子態(tài)矢,給出其密度算符和歸一化系數(shù);接著研究其量子統(tǒng)計(jì)屬性,包括光子數(shù)分布、平均光子數(shù)和亞泊松分布以及壓縮特點(diǎn)等;特別研究了該量子態(tài)的Wigner函數(shù)及其負(fù)部體積;最后進(jìn)行簡(jiǎn)單的總結(jié).

2 三頭貓態(tài)

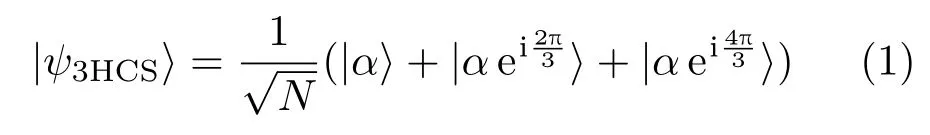
其密度算符為

其中

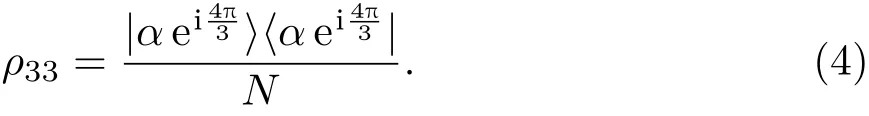
由于Tr(ρ3HCS)=1,根據(jù)相干態(tài)的內(nèi)積關(guān)系

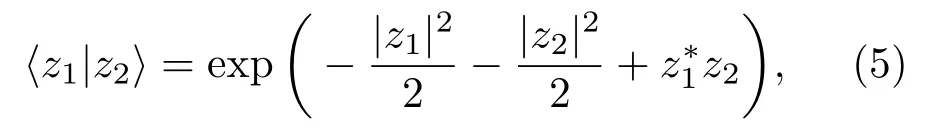
可得歸一化系數(shù)為

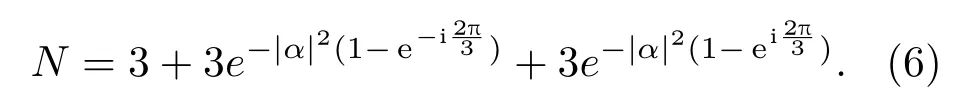
接下來(lái),我們對(duì)照相干態(tài)、二頭貓態(tài)和四頭貓態(tài),分析研究三頭貓態(tài)的量子統(tǒng)計(jì)屬性.附錄中給出了二頭貓態(tài)和四頭貓態(tài)的一些量子屬性的解析表達(dá)式.

3 量子統(tǒng)計(jì)屬性

3.1 光子數(shù)分布

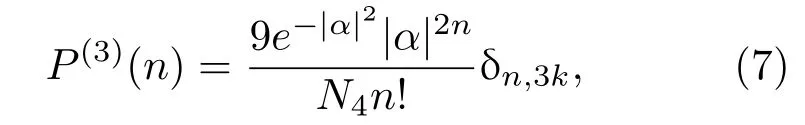
3.2 平均光子數(shù)

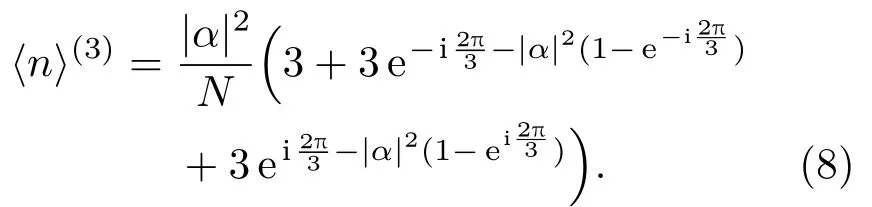
另外,二頭貓態(tài)和四頭貓態(tài)的平均光子數(shù)的表達(dá)式見附錄.

圖1給出了相干態(tài)、二頭貓態(tài)、三頭貓態(tài)和四頭貓態(tài)的平均光子數(shù)的變化情形.結(jié)果發(fā)現(xiàn),當(dāng)幅度|α|∈[0,1.5]的情況下,相干態(tài)、二頭貓態(tài)、三頭貓態(tài)和四頭貓態(tài)的平均光子數(shù)依次減小;而當(dāng)|α|∈[1.5,2.2]的情況下,相干態(tài)、二頭貓態(tài)、三頭貓態(tài)和四頭貓態(tài)的平均光子數(shù)依次增大.對(duì)于大幅度|α|的情況下,這幾種量子態(tài)的平均光子數(shù)幾乎是相等的.

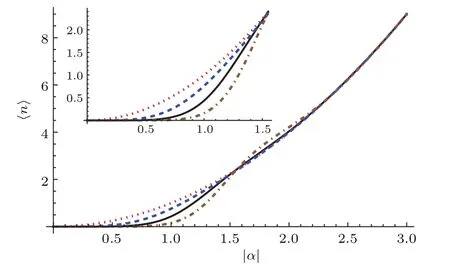
圖1 相干態(tài)(點(diǎn)線)、二頭貓態(tài)(劃線)、三頭貓態(tài)(實(shí)線)和四頭貓態(tài)(點(diǎn)劃線)的平均光子數(shù)隨|α|的變化Fig.1.Average photon numbers as the function of the amplitude|α|for CS(dotted line),2HCS(dashed line),3HCS(solid line)and 4HCS(dotdashed line).

3.3 亞泊松統(tǒng)計(jì)

光場(chǎng)的非經(jīng)典性可以通過(guò)觀察其是否具有亞泊松分布的特點(diǎn)來(lái)判斷.亞泊松分布的特點(diǎn)可以借助Mandel提出的QM參數(shù)[13]來(lái)表征,其定義為

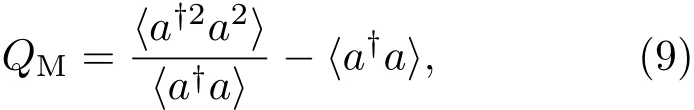
該參數(shù)反映了所考慮的光場(chǎng)與具有泊松分布特征的相干態(tài)光場(chǎng)光子數(shù)分布偏離情況.當(dāng)QM=0時(shí),光場(chǎng)為泊松分布,而當(dāng)QM＞0(或QM＜0)時(shí),則稱光場(chǎng)具有超(或亞)泊松分布.對(duì)于相干態(tài),易知QM=0,這也表明相干態(tài)具有泊松統(tǒng)計(jì)分布的特點(diǎn).

在圖2給出了二頭貓態(tài)、三頭貓態(tài)以及四頭貓態(tài)的QM參數(shù)隨|α|變化的圖形.從圖2(a)可見三頭貓態(tài)QM參數(shù)的負(fù)值部分出現(xiàn)在一個(gè)特殊的區(qū)域范圍,即|α|∈[1.77,2.55],也就是說(shuō),當(dāng)在該范圍取參數(shù),三頭貓態(tài)呈現(xiàn)亞泊松統(tǒng)計(jì)的非經(jīng)典特點(diǎn).而且,最小的QM值大約為?0.05,當(dāng)|α|大約取1.95時(shí).二頭貓態(tài)則不同,因?yàn)槎^貓態(tài)對(duì)于任何的|α|,都不能出現(xiàn)亞泊松分布的特點(diǎn),見圖2(b).但與四頭貓態(tài)相對(duì)比,似乎具有類似的結(jié)論,但四頭貓態(tài)最小的QM值大約為?0.225,當(dāng)|α|大約取2時(shí),見圖2(c).

圖2 QM參數(shù)隨|α|的變化 (a)三頭貓態(tài);(b)二頭貓態(tài);(c)四頭貓態(tài)Fig.2.Mandel Q parameter as a function of|α|for(a)3HCS,(b)2HCS,(c)4HCS.

3.4 正交壓縮效應(yīng)

接下來(lái),我們研究另一種非經(jīng)典效應(yīng),即某正交分量的壓縮[14].定義正交算符和它們所對(duì)應(yīng)的方差可以分別表達(dá)為

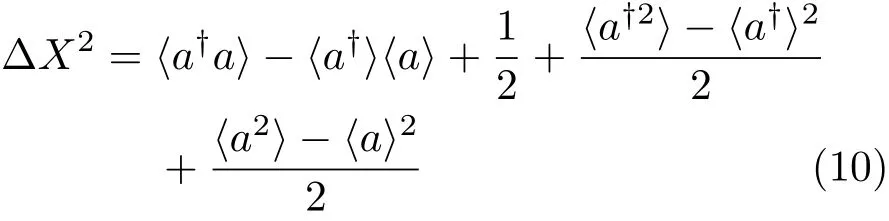
和

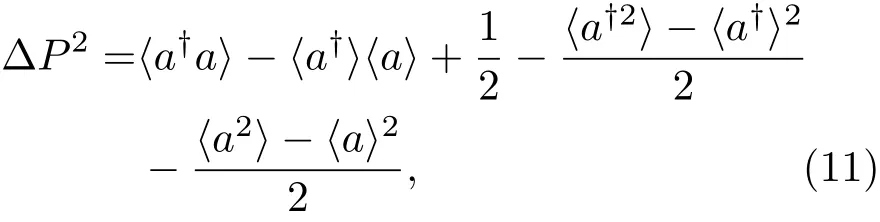
且滿足不確定性關(guān)系?X2?P2≥1/4.對(duì)于真空態(tài)(或相干態(tài)),如果某個(gè)量子態(tài)的?X2和?P2二者之一小于1/2,那么該量子態(tài)就是壓縮態(tài).另外,我們可以通過(guò)dB[X]=和dB[P]=用分貝(dB)的形式來(lái)描述量子壓縮特點(diǎn).也就是說(shuō),如果dB[X]和dB[P]二者之一小于0,那么該量子態(tài)就是壓縮態(tài).

經(jīng)過(guò)計(jì)算,我們發(fā)現(xiàn)所考慮的三頭貓態(tài)的

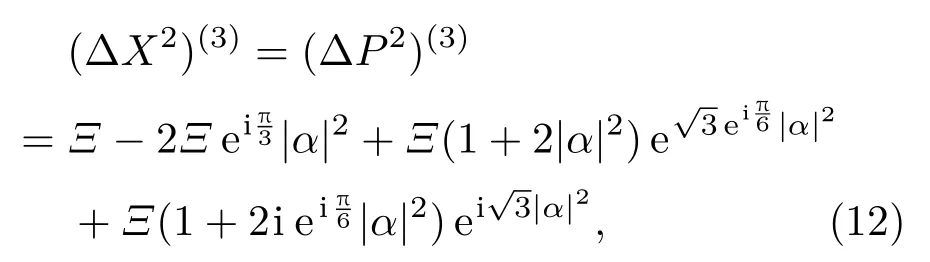
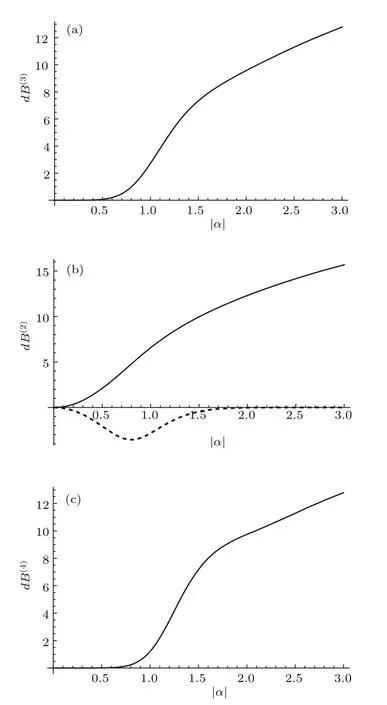
圖3 壓縮dB參數(shù)隨|α|的變化 (a)三頭貓態(tài);(b)二頭貓態(tài);(c)四頭貓態(tài).Fig.3.Squeezed dB parameters as a function of|α|for(a)3HCS,(b)2HCS,(c)4HCS.

4 Wigner函數(shù)

Wigner函數(shù)是量子相空間理論的重要組成部分[15].由于其非正定性特點(diǎn),故不能成為一個(gè)真正意義上的概率分布函數(shù).通常,我們可以根據(jù)量子態(tài)的Wigner負(fù)值來(lái)判斷其非經(jīng)典性特點(diǎn)[16,17].

4.1 Wigner函數(shù)的推導(dǎo)

我們首先推導(dǎo)出其Wigner函數(shù)的解析表達(dá)式.根據(jù)公式[18]

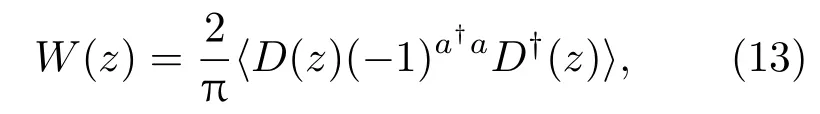
這里需要說(shuō)明的是,(?1)a?a為奇偶宇稱算符,為平移算符,且

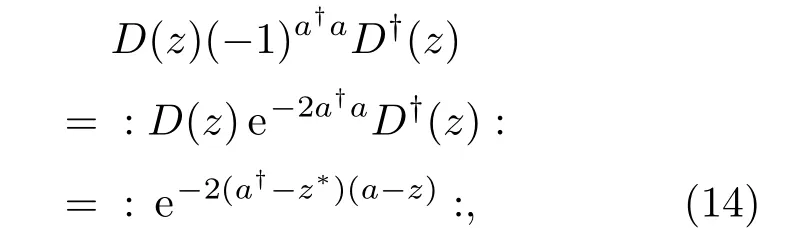
這里平移算符可以直接進(jìn)入正規(guī)排序.這樣,我們很容易得到三頭貓態(tài)的Wigner函數(shù)為

其中

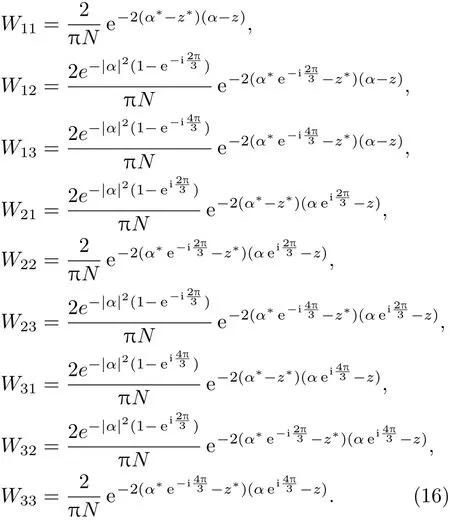
利用(15)式,圖4給出了幾種情形下三頭貓態(tài)的Wigner函數(shù).從圖中可以發(fā)現(xiàn),對(duì)于較小幅度的三頭貓態(tài),其負(fù)部區(qū)域不明顯(如圖4(a));隨著幅度|α|的增大,發(fā)現(xiàn)負(fù)部區(qū)域數(shù)量增多了.另外,我們通過(guò)數(shù)值分析發(fā)現(xiàn),對(duì)于|α|相同的三頭貓態(tài),其分布圖形會(huì)隨著θ的變化而發(fā)生旋轉(zhuǎn),但總體形狀沒(méi)有改變.

為了更清楚地展示三頭貓態(tài)與相干態(tài)、二頭貓態(tài)及四頭貓態(tài)Wigner函數(shù)的區(qū)別,我們繪制了相同情形下(|α|=1,θ=0)這幾種量子態(tài)的Wigner函數(shù)圖形.圖5(a)說(shuō)明相干態(tài)的Wigner函數(shù)無(wú)負(fù)部區(qū)域,其分布中心與α有關(guān);圖5(b)表明二頭貓態(tài)出現(xiàn)負(fù)部區(qū)域,且具有π旋轉(zhuǎn)對(duì)稱特點(diǎn),圖5(c)對(duì)應(yīng)三頭貓態(tài),出現(xiàn)了負(fù)部區(qū)域,具有2π/3旋轉(zhuǎn)對(duì)稱的特點(diǎn);圖5(d)對(duì)應(yīng)四頭頭貓態(tài),出現(xiàn)負(fù)部區(qū)域,且具有π/2旋轉(zhuǎn)對(duì)稱特點(diǎn).

圖4 三頭貓態(tài)的 Wigner函數(shù)圖(θ=0) (a)|α|=0.2;(b)|α|=1;(c)|α|=2;(d)|α|=3Fig.4.Wigner functions of 3HCS with(θ=0),and(a)|α|=0.2,(b)|α|=1,(c)|α|=2,(d)|α|=3.

圖5 幾種量子態(tài)的Wigner函數(shù)圖(|α|=1,θ=0) (a)相干態(tài);(b)二頭貓態(tài);(c)三頭貓態(tài);(d)四頭貓態(tài)Fig.5.Wigner functions with|α|=1,θ=0 for(a)CS,(b)2HCS,(c)3HCS,(d)4HCS.

4.2 Wigner函數(shù)的負(fù)部體積

通過(guò)前面的研究發(fā)現(xiàn),相干態(tài)沒(méi)有出現(xiàn)負(fù)值,但二頭、三頭和四頭貓態(tài)都會(huì)出現(xiàn)了負(fù)值,而且隨著|α|的增大,分布更復(fù)雜,波包形狀發(fā)生振蕩,負(fù)部體積更明顯.Wigner函數(shù)的負(fù)部體積δ是反映光場(chǎng)非經(jīng)典性的一個(gè)重要標(biāo)志[19],其定義如下∶

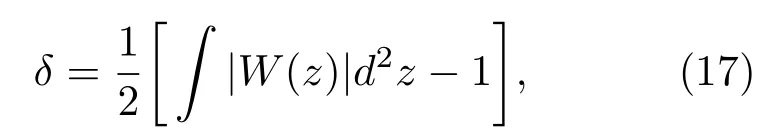
只要量子態(tài)的Wigner函數(shù)已知,通過(guò)數(shù)值積分就可以得到負(fù)部區(qū)域體積.根據(jù)定義,相干態(tài)的δ都為零.

圖6給出了二頭、三頭和四頭貓態(tài)的Wigner函數(shù)的負(fù)部體積δ在一定范圍內(nèi)隨|α|的變化圖形,這里需要說(shuō)明的是,δ的大小與θ的選取是無(wú)關(guān)的.我們發(fā)現(xiàn),在小幅度范圍,這三種量子態(tài)的δ幾乎為零;但隨著|α|的增大,負(fù)部體積δ逐漸增大,直至趨于相應(yīng)的上限值(δ(2)～0.3,δ(3)～0.6,δ(4)～ 0.8).

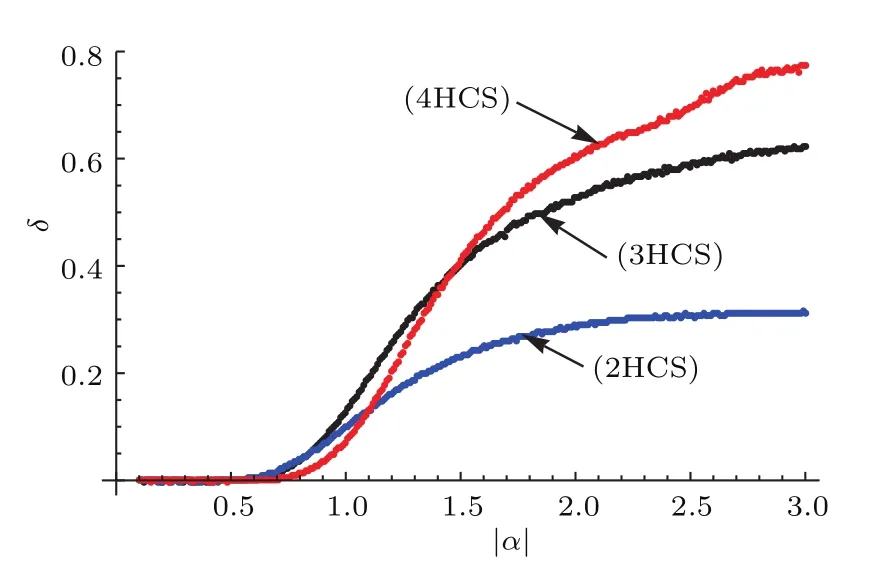
圖6 二頭貓態(tài)、三頭貓態(tài)和四頭貓態(tài)的負(fù)部體積δ隨|α|的變化Fig.6.Negative volume of the Wigner functions for 2HCS,3HCS and 4HCS as a function of|α|.

5 討論和結(jié)論

我們研究了一種相位型三頭薛定諤貓態(tài)的量子統(tǒng)計(jì)屬性.從三頭貓態(tài)的態(tài)矢出發(fā),給出其密度算符并進(jìn)行了歸一化,然后詳細(xì)研究了其一些量子統(tǒng)計(jì)屬性,這些屬性包括光子數(shù)分布、平均光子數(shù)、亞泊松分布、壓縮效應(yīng)以及Wigner函數(shù)的負(fù)部體積特點(diǎn).為反映出其非經(jīng)典性質(zhì),重要結(jié)論總結(jié)如下∶1)三頭貓態(tài)不是壓縮態(tài),沒(méi)有展現(xiàn)出壓縮效應(yīng);2)在適當(dāng)選取參數(shù)的情況下,可以表現(xiàn)出亞泊松分布的特點(diǎn);3)三頭貓態(tài)的Wigner函數(shù)會(huì)出現(xiàn)負(fù)值特點(diǎn).

另外,我們還分析了三頭貓態(tài)與相干態(tài)、二頭貓態(tài)以及四頭貓態(tài)的量子統(tǒng)計(jì)屬性的異同.相比二頭貓態(tài),三頭貓態(tài)無(wú)壓縮但呈現(xiàn)泊松分布特點(diǎn);相比四頭貓態(tài),三頭貓態(tài)具有類似的非經(jīng)典性特點(diǎn),但相對(duì)更弱些.前面已經(jīng)提到,二頭貓態(tài)和四頭貓態(tài)在量子精密測(cè)量和量子信息處理中都得到了相應(yīng)的應(yīng)用.作為介于二者之間的三頭貓態(tài),也將發(fā)揮其作用.例如,利用三頭貓態(tài)作為信號(hào)源,通過(guò)分束器或非線性介質(zhì),可以產(chǎn)生相應(yīng)的糾纏源,應(yīng)用于量子信息技術(shù)[20?22].

附錄A 三頭貓態(tài)的統(tǒng)計(jì)期望值

這樣,我們可以通過(guò)取不同的k和l,得到正文中所需的各種期望值.

附錄B 相位型二頭貓態(tài)的定義及其屬性

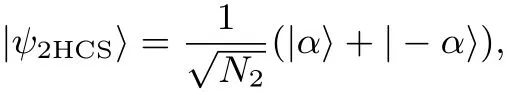
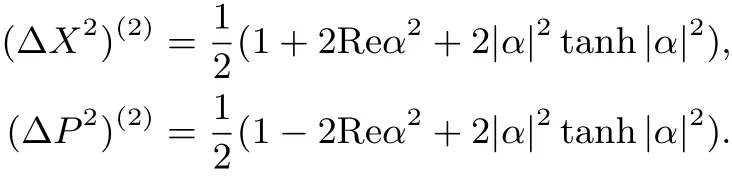
另外,二頭貓態(tài)的Wigner函數(shù)為

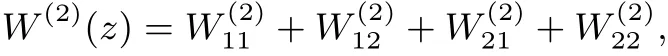
其中

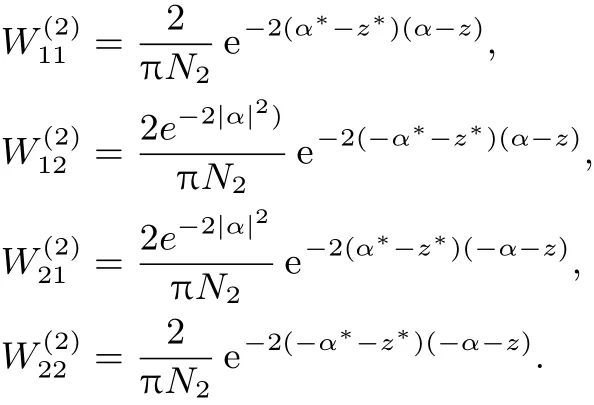
附錄C 相位型四頭貓態(tài)的定義及其屬性

定義一種相位型四頭貓態(tài)

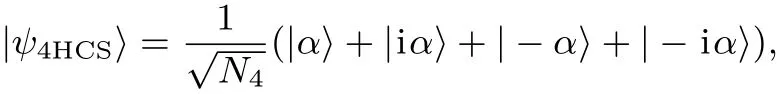
由此可得

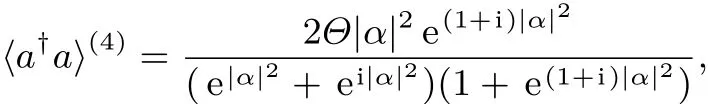
QM參數(shù)

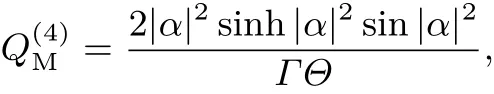
以及正交分量方差

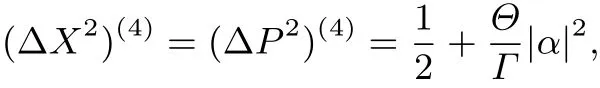
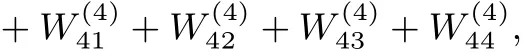
其中

[1]Dirac P A M 1958 The Principles of Quantum Mechanics(4th Ed.)(Oxford:Oxford University Press)pp1–22

[2]Zeng J Y 2007 Quantum Mechanics(4th Ed.)(Beijing:Science Press)pp52–54[曾謹(jǐn)言 2007量子力學(xué)(第四版)(北京:科學(xué)出版社)]pp52–54

[3]Dell’Anno F,de Siena S,Illuminatif2006 Phys.Rep.428 53

[4]Kok P,Lovett B W 2010 Introduction to Optical Quantum Information Processing(Cambridge:Cambridge University Press)pp183–187

[5]Polkinghorne J C 1985 The Quantum World(Princeton:Princeton University Press)p67

[6]John G 2011 In Search of Schrodinger’s Cat:Quantum Physics and Reality(Berlin:Random House Publishing Group)pp234

[7]Glauber R J 1963 Phys.Rev.131 2766

[8]Gerry C C,Knight P 2005 Introductory Quantum Optics(Cambridge:Cambridge University Press)pp174–181

[9]Yukawa M,Miyata K,Mizuta T,Yonezawa H,Marek P,Filip R,Furusawa A 2013 Opt.Express 21 5529

[10]Vlastakis B,Kirchmair G,Leghtas Z,Nigg S E,Frunzio L,Girvin S M,Mirrahimi M,Devoret M H,Schoelkopf R J 2013 Science 342 607

[11]Raimond J M,Facchi P,Peaudecerf B,Pascazio S,Sayrin C,Dotsenko I,Gleyzes S,Brune M,Haroche S 2012 Phys.Rev.A 86 032120

[12]Lee S Y,Lee C W,Nha H,Kaszlikowski D 2015 J.Opt.Soc.Am.B 32 1186

[13]Mandel L 1979 Opt.Lett.4 205

[14]Walls D F,Milburn G J 1994 Quantum Optics(Berlin:Springer-Verlag)pp81–82

[15]Wigner E P 1932 Phys.Rev.40 749

[16]Xu X X,Yuan H C,Hu L Y 2010 Acta Phys.Sin.59 4661

[17]Xu X X,Yuan H C 2016 Phys.Lett.A 380 2342

[18]Lutterbach L,Davidovich L 1997 Phys.Rev.Lett.78 2547

[19]Kenfack A,Zyczkowski K 2004 J.Opt.B:Quantum Semi-Class.Opt.6 396

[20]Gerry C C,Mimih J 2010 Contemp.Phys.51 497

[21]Leghtas Z,Kirchmair G,Vlastakis B,Schoelkopf R J,Devorett M H,Mirrahimi M 2013 Phys.Rev.Lett.111 120501

[22]Ralph T C,Gilchrist A,Milburn G J,Munro W J,Glancy S 2003 Phys.Rev.A 68 042319

PACS∶42.50.Dv,03.65.—wDOI∶10.7498/aps.66.104201

*Project supported by National Natural Science Foundation of China(Grant No.11665013),Research on Teaching Reform of Jiangxi Higher Education,China(Grant No.JXJG-16-2-2)and the Gaoyuan Plan Project of Jiangxi Normal University,China.

?Corresponding author.E-mail:xuxuexiang@jxnu.edu.cn

Quantum statistical properties of phase-type three-headed Schrodinger cat state?

Lin Dun-Qing1)Zhu Ze-Qun1)Wang Zu-Jian1)Xu Xue-Xiang1)2)?
1)(College of Physics and Communication Electronics,Jiangxi Normal University,Nanchang 330022,China)
2)(Center for Quantum Science and Technology,Jiangxi Normal University,Nanchang 330022,China)

25 December 2016;revised manuscript

8 March 2017)

Quantum superposition is a fundamental principle of quantum mechanics,which provides a crucial basis to observe phenomena beyond the predictions of classical physics.For example,a quantum entangled state can exhibit stronger correlation than classically possible one.In quantum state engineering,many new quantum states can be obtained from the superposition of many known states.

In recent decades,the superposition of coherent states(CSs)with the same amplitude but two different phases has been a subject of great interest.This superposition state was often called Schrodinger cat state(here,we also name it 2-headed cat state(2HCS)),which becomes an important tool to study a lot of fundamental issues.Surprisingly,some studies have extended the quantum superposition to involving more than two component coherent states.In order to produce the superposition of three photons,people have considered the superposition of coherent states with three different phases(here,we also name it 3-headed cat state(3HCS)).Furthermore,in microwave cavity quantum electrodynamics of bang-bang quantum Zeno dynamics control,people have proposed the superposition of coherent states with four different phases(here,we also name it 4-headed cat state(4HCS)).

In this paper,we make a detailed investigation on the quantum statistical properties of a phase-type 3HCS.These properties include photon number distribution,average photon number,sub-Poissionian distribution,squeezing effect,and Wigner function,etc.We derive their analytical expressions and make numerical simulations for these properties.The results are compared with the counterparts of the CS,the 2HCS and the 4HCS.

The conclusions are obtained as follows.1)The CS,the 2HCS,the 3HCS and the 4HCS have k,2k,3k and 4k photon number components,respectively(k is an integer);2)small difference in average photon number among these quantum states in small-amplitude range can be observed,while their average photon numbers become almost equal in large-amplitude range;3)the CS exhibits Poisson distribution,and the 2HCS,the 3HCS and the 4HCS exhibit super-Poisson distributions in most amplitude ranges,however,sub-Poisson distribution can be seen for the 3HCS and the 4HCS in some specific amplitude ranges;4)except for the 2HCS that may have the squeezing property,no squeezing properties can be found in the CS,the 3HCS and the 4HCS;5)negative values can exist in the Wigner functions for the 2HCS,the 3HCS and the 4HCS,while it is not found in the CS.

Similar to the 2HCS and 4HCS,the Wigner function of the 3HCS has negative component,which implies its nonclassicality.Different from the 2HCS,the 3HCS exhibits sub-Poisson photon number distribution in a certain amplitude range,it is weaker than that of the 4HCS.At the same time,no squeezing is found in the 3 or 4HCS,which is another difference from the 2HCS.

∶Schrodinger cat state,three-headed cat state,nonclassicality,Wigner function

?國(guó)家自然科學(xué)基金(批準(zhǔn)號(hào):11665013)、江西省高等學(xué)校教學(xué)改革研究課題(批準(zhǔn)號(hào):JXJG-16-2-2)和江西師范大學(xué)團(tuán)隊(duì)高原計(jì)劃項(xiàng)目資助的課題.

?通信作者.E-mail:xuxuexiang@jxnu.edu.cn

?2017中國(guó)物理學(xué)會(huì)Chinese Physical Society