各向異性界面動力學與各向異性表面張力的相互作用對定向凝固過程中深胞晶生長的影響

蔣晗 陳明文 王濤 王自東?

1)(北京科技大學材料科學與工程學院,北京 100083)

2)(北京科技大學數理學院,北京 100083)

各向異性界面動力學與各向異性表面張力的相互作用對定向凝固過程中深胞晶生長的影響

蔣晗1)陳明文2)?王濤1)王自東1)?

1)(北京科技大學材料科學與工程學院,北京 100083)

2)(北京科技大學數理學院,北京 100083)

(2017年1月5日收到;2017年2月26日收到修改稿)

通過應用匹配漸近展開法和多變量展開法研究了各向異性界面動力學與各向異性表面張力的相互作用對定向凝固過程中深胞晶生長的影響.結果表明∶當各向異性界面動力學與各向異性表面張力的偏好方向之間相差角度為θ0時,θ0會對深胞晶生長形態產生影響;當0≤θ0≤π/4時,隨著θ0的增大,深胞晶的指狀界面全長減小,深胞晶根部的深度減小,根部附近界面的曲率減小,而曲率半徑增大;當π/4≤θ0≤π/2時,隨著θ0的增大,深胞晶的指狀界面全長增大,深胞晶根部的深度增大,根部附近界面的曲率增大,而曲率半徑減小.

∶定向凝固,各向異性表面張力,各向異性界面動力學,深胞晶生長

PACS∶68.70.+w,81.10.Aj,81.30.FbDOI∶10.7498/aps.66.106801

1 引 言

幾十年來,定向凝固過程中的深胞晶生長一直是凝聚態物理和材料科學的研究重點.已經有許多實驗和數值模擬[1?4]通過使用Hele-Shaw模型對深胞晶生長問題進行了研究.Hele-Shaw模型包括細長的樣本材料及兩個恒溫區∶一個高于平直界面液化溫度TM的高溫區(溫度為TH)和一個低于TM的低溫區(溫度為TC).以恒定速度V由高溫區向低溫區拉動樣本,隨著拉速V的增加,固液界面由低速生長的平直界面依次演變為小振幅的胞晶界面、大振幅的深胞晶界面、枝晶界面、細胞晶界面,最后變為高速生長的平直界面.Xu等[5,6]在Mullins和Sekerka[7,8]建立的平界面形態線性穩定性理論(稱為M-S理論)基礎上,運用Saffmen-Taylor[9]曲線坐標得到了各向同性表面張力下的深胞晶形態的近似解析解.大量的研究表明,各向異性表面張力和各向異性界面動力學都會對胞晶生長的界面形態產生影響.Etsuro和Sekerka[10]發現各向異性表面張力和各向異性界面動力學是胞晶生長存在優選方向的根本原因.王志軍等[11,12]和Trivedi等[13]分別研究了各向異性表面張力和各向異性界面動力學對定向凝固過程中胞晶微結構生長方向的影響,發現各向異性表面張力和各向異性界面動力學都會使胞晶界面傾斜生長.陳明文等[14,15]研究了考慮表面張力和界面動力學各向異性的定向凝固過程中深胞晶生長的界面形態,揭示了深胞晶界面微結構形態形成的物理機制.本文研究了各向異性表面張力和各向異性界面動力學的相互作用對深胞晶生長形態的影響,即各向異性表面張力和各向異性界面動力學的偏好方向不一致,相差角度為θ0時,θ0會對深胞晶生長形態產生影響.

2 定向凝固系統的數學模型

考慮定向凝固過程中的樣本材料是細長的深胞晶生長,凝固過程可視為二維.且二元混合系統中的次組元為稀釋的雜質;忽略固相內的溶質擴散;除擴散系數外的熱力學性質在固相和液相內是相同的,系統不存在對流.該系統下的深胞晶生長,其液相位于上半空間,界面拉伸速度為V,方向指向為液相方向向上.界面隨著時間的變化向上移動,設原點位于胞晶尖端的直角坐標系Oxy中,溫度梯度為GT,遠場濃度為C∞,胞晶列的周期為lw.

選取深胞晶尖端曲率半徑lt為長度尺度,lD=κD/V為溶質擴散長度,其中κD為溶質擴散系數. 本文假定深胞晶尖端曲率半徑遠遠小于溶質擴散長度,即lt?lD.選取Péclet數Pe=ε=lt/lD為小參數,拉速V為速度尺度,lt/V為時間尺度,?H/(cpρ)為溫度尺度,其中?H為單位體積內固相產生的潛熱,cp為液相比熱,ρ為熔體密度,遠場濃度C∞為濃度尺度.于是,熱傳導方程、溶質擴散方程和界面上的界面方程轉化為無量綱的控制方程.

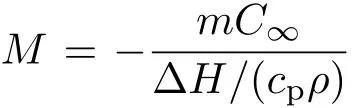
由于解具有周期性,可以僅考慮單個胞晶,且胞晶側壁為x=±W,W為自由參數.假定矩形坐標(x,y)的原點位于胞晶的尖端,生長區域的溫度分布近似為僅與y有關的線性函數,為T=εG(y?y0),其中y0為坐標原點到溫度為液化溫度TL=0的距離.選用Saffmen-Taylor(ST)解[9]構造曲線坐標系(ξ,η).將Hele-Shaw流的流函數和勢函數用Ψ=(X,Y)和Φ=(X,Y)表示,且有

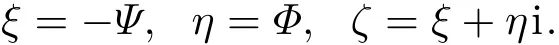
Saffmen-Taylor解可以轉化為

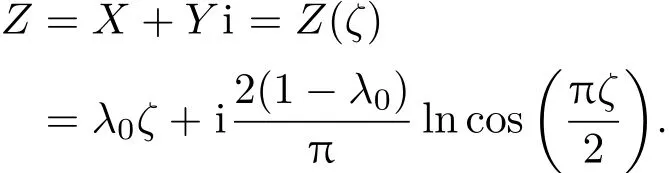
曲線坐標于直角坐標系的轉化關系為

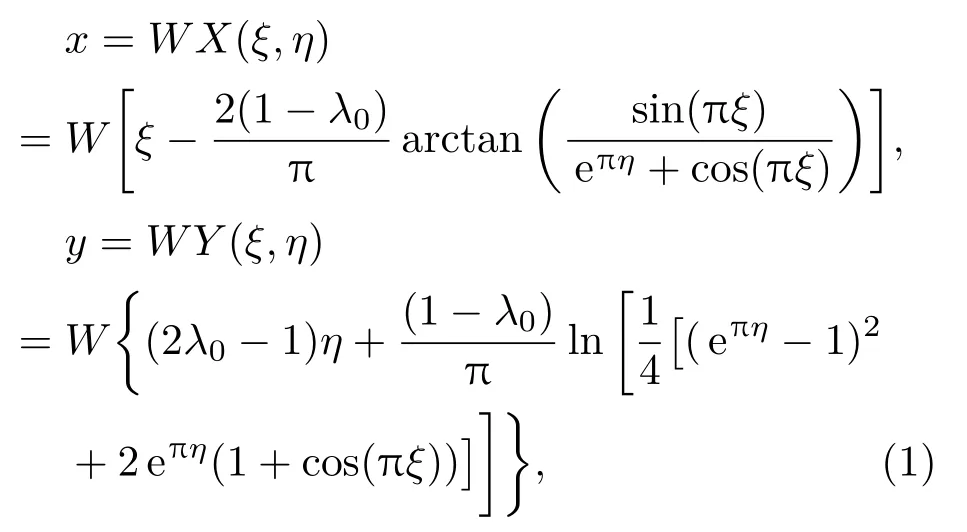
其中λ0是漸近寬度系數.

考慮4重對稱的晶體的表面張力系數

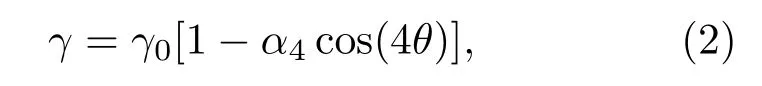
其中γ0是各向同性表面張力系數,α4是各向異性表面張力系數,θ是界面法向量與Oy軸之間的夾角.

界面動力學系數

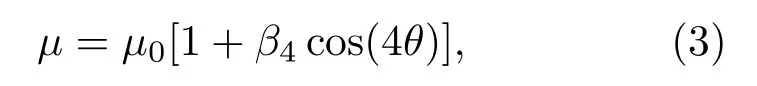
其中μ0是各向同性界面動力學系數,β4是各向異性界面動力學系數.

在Saffmen-Taylor曲線坐標系下

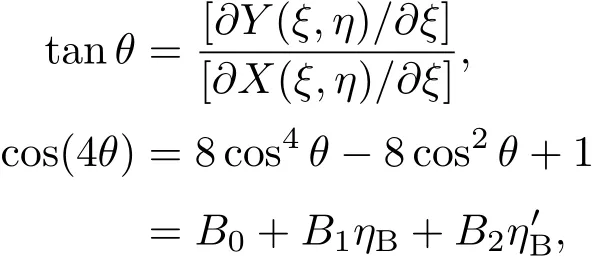
由(2)式,各向異性的表面張力參數變為

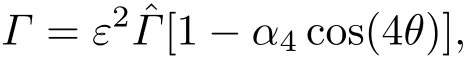
則有

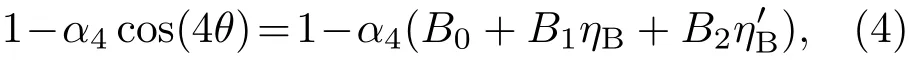
其中

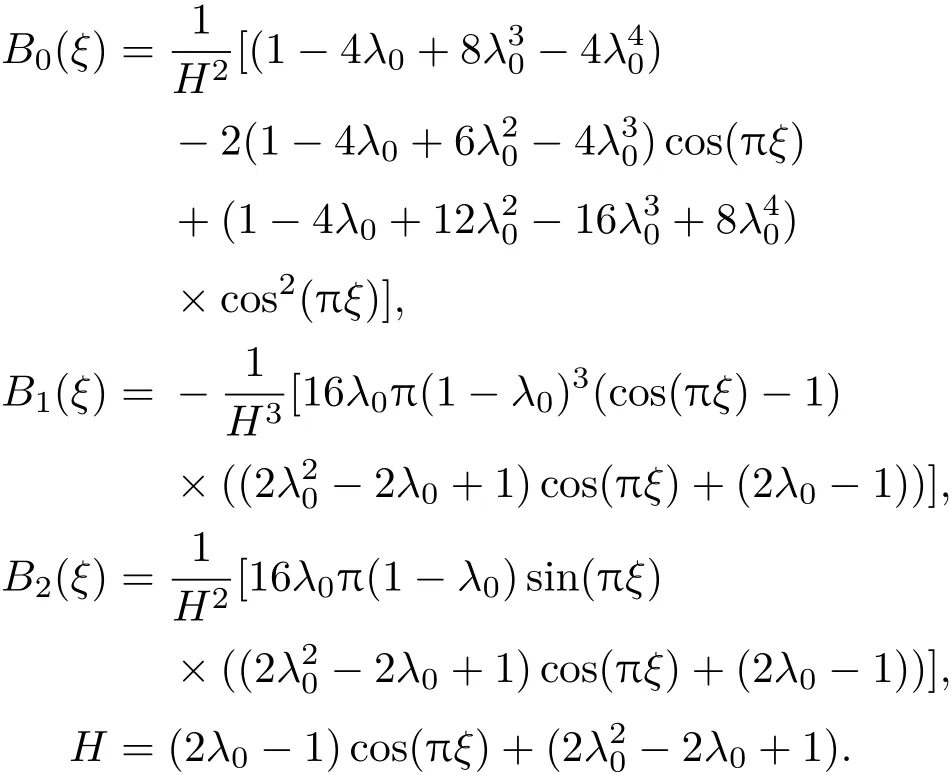
由(3)式,各向異性的界面動力學參數變為

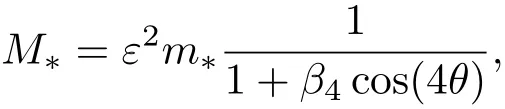
則有

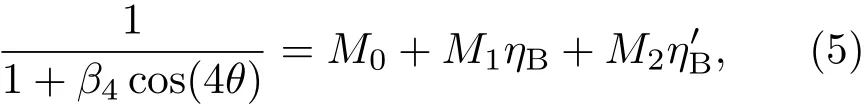
其中

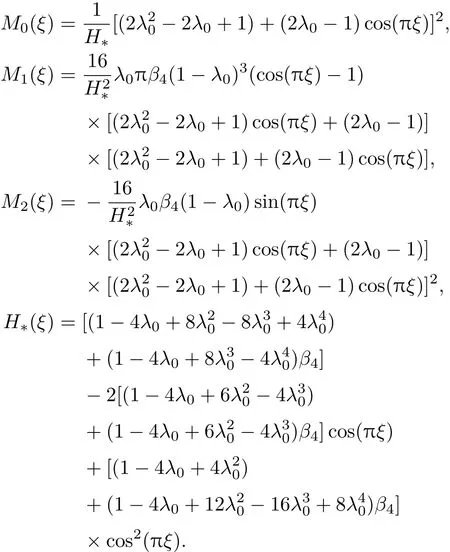
當各向異性表面張力和各向異性界面動力學的偏好方向之間相差角度為θ0時,表面張力系數可以表示為[16]

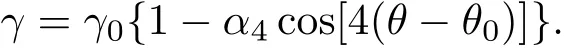
由于

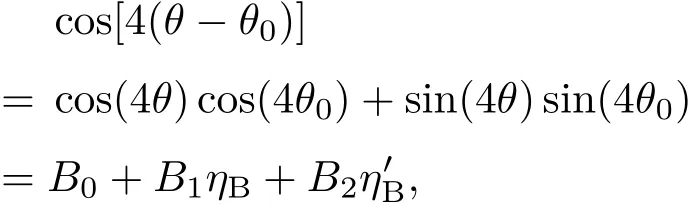
則B0(ξ),B1(ξ),B2(ξ)變為

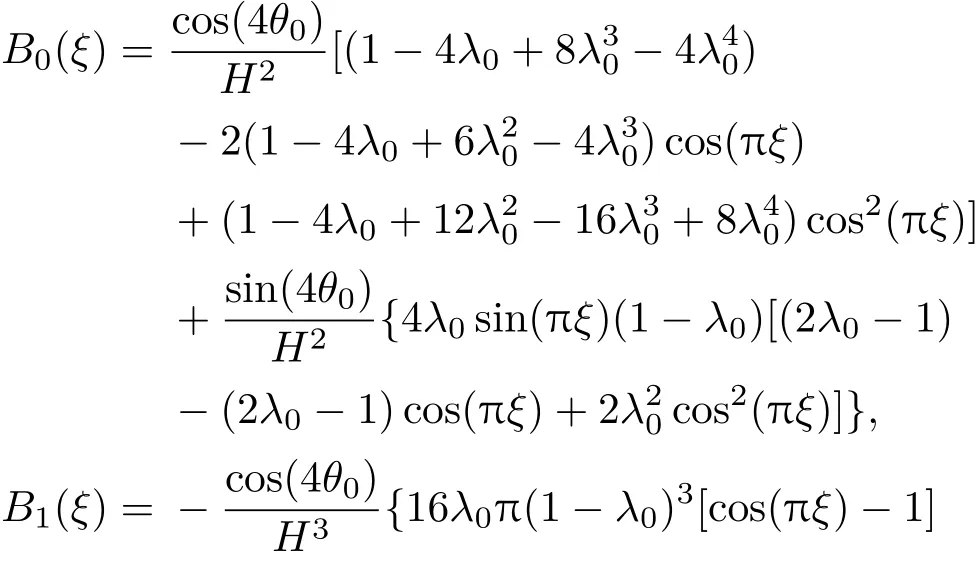
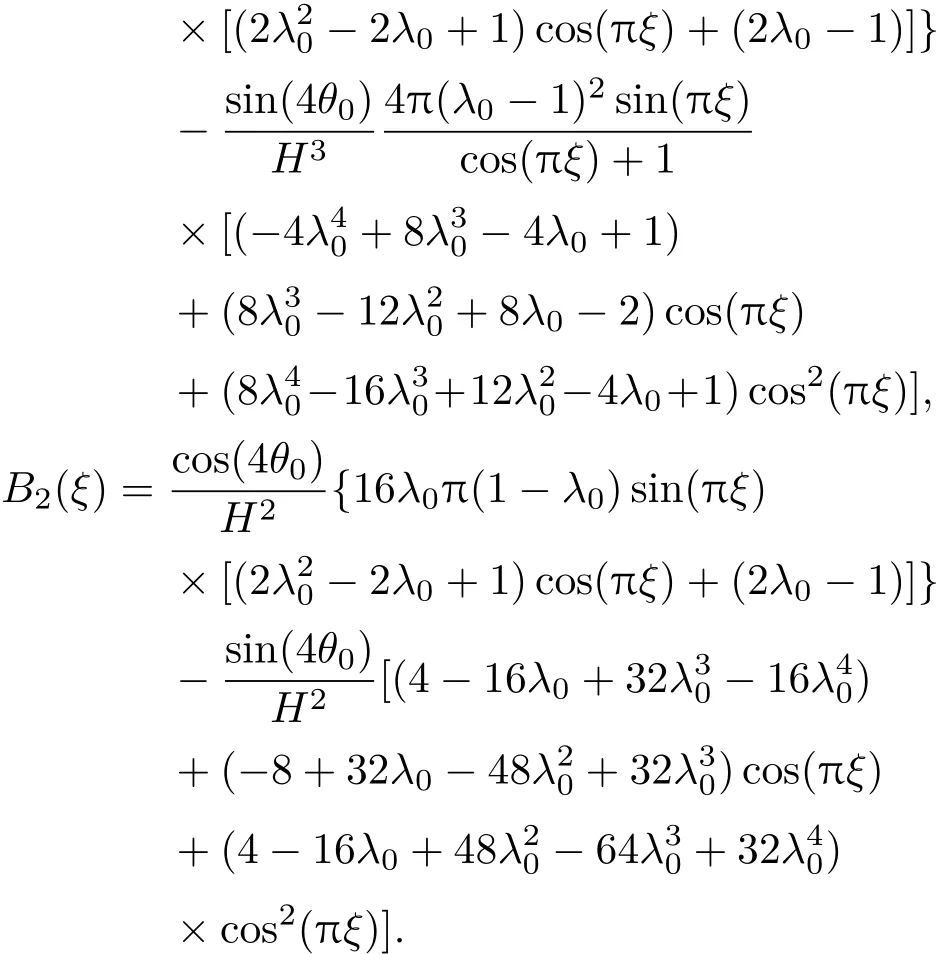
在曲線坐標系(ξ,η)下,整個物理空間被分為遠離根部的外部區域和根部附近的內部區域.

深胞晶生長的穩態解(C,ηB)滿足控制方程

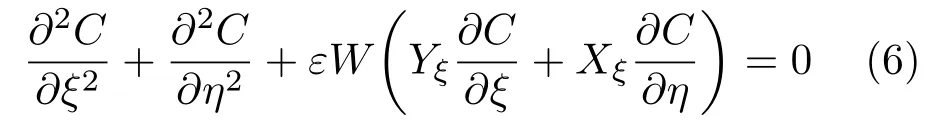
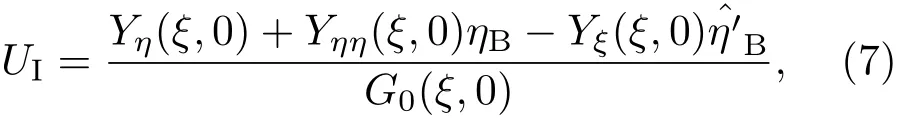
則Gibbs-Thomson條件為

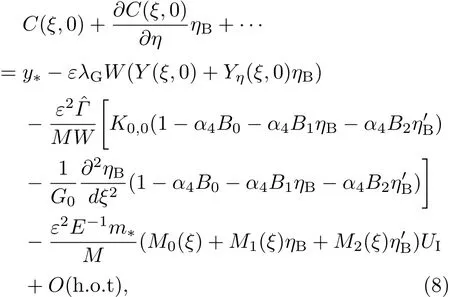
質量守恒條件為

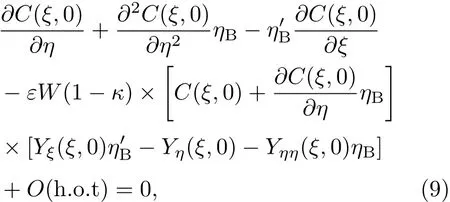
其中κ為分離系數,O(h.o.t)為高階項,

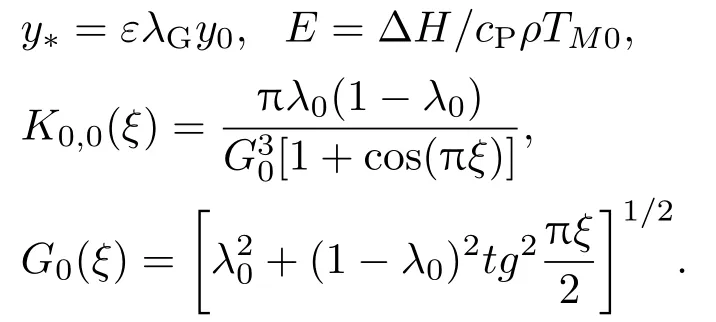
在胞晶尖端,當ξ=η=0時,

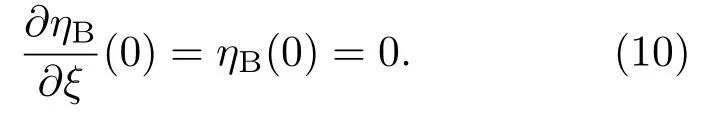
在根部底端,當ξ=±1,η=ηb時,

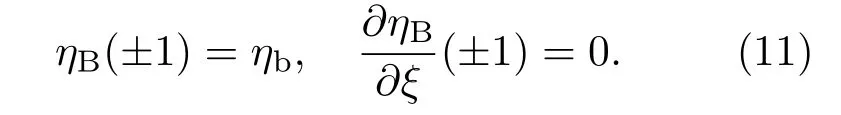
在胞晶側壁,當ξ=±1時,

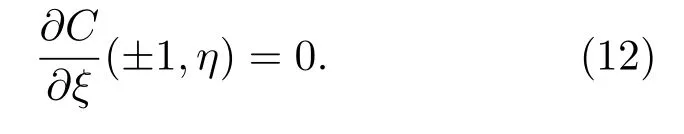
在遠場處,當η→∞時,

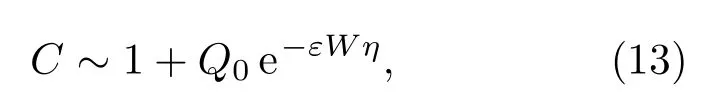
其中Q0是與變量ξ和η無關的常數.

3 外部區域的漸近解

控制方程(6),界面條件(8)和(9),尖端光滑條件(10),側壁條件(12)和遠場條件(13)組成了一個非齊次的外部系統,該非齊次系統有如下形式的解[5]∶

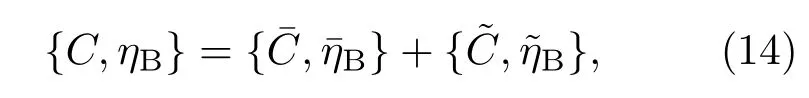
運用文獻[5]中的方法得到(14)式中非齊次系統的漸近解為

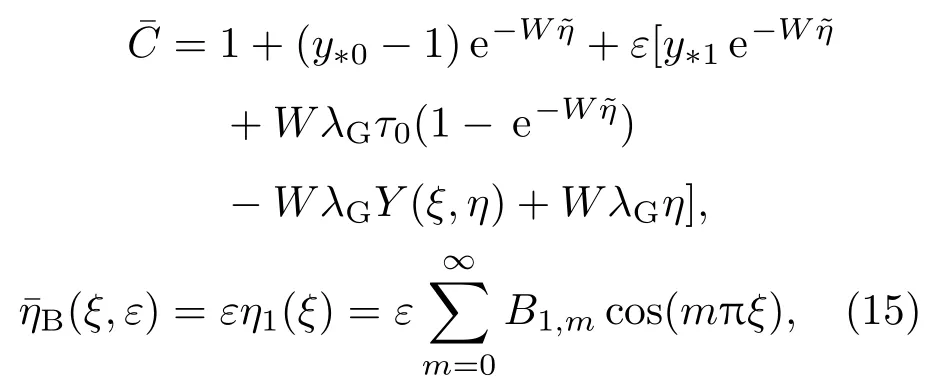
其中

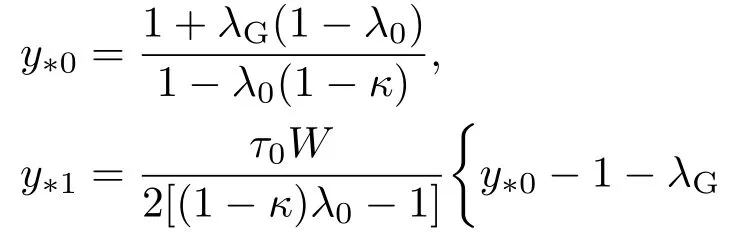
(14)式中齊次系統的通解為

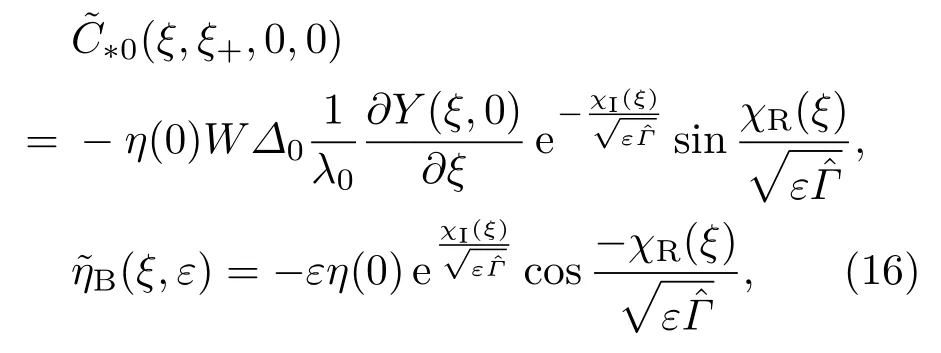
其中

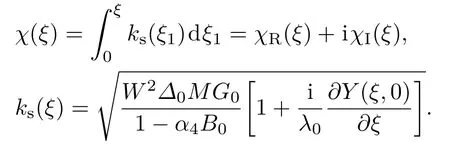
將(15)與(16)式進行匹配,可以得到外解為

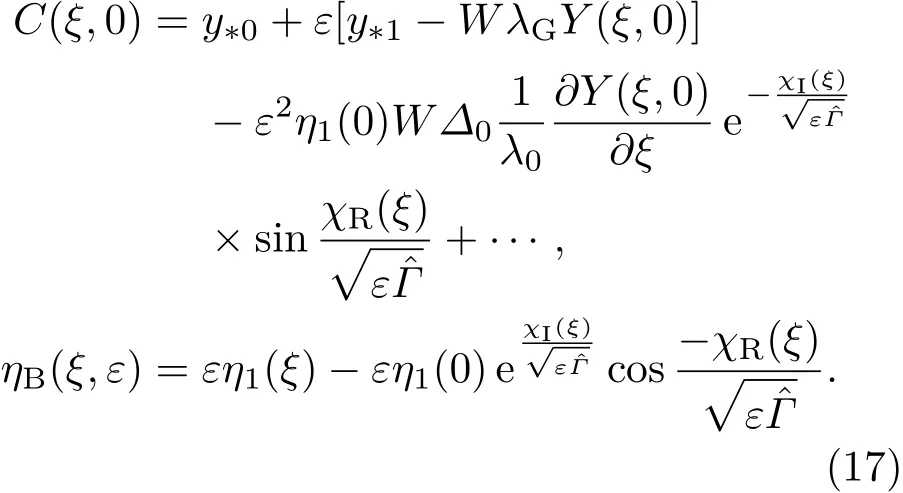
4 根部區域的漸近解

由于外解(17)式在ξ=±1處不滿足根部光滑條件,因此外解不能提供根部底端的位置,需要求根部區域的內解.當ξ→?1時,由(15)式有

設η=ηT(ξ)為根部區域的中心線,并且是根部區域界面形狀函數的近似. 在根部區域引入內部變量和

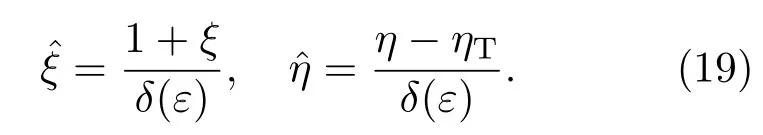
由(18)式,在根部區域的遠場有

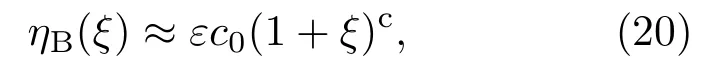
為了與外解匹配,根部的遠場滿足

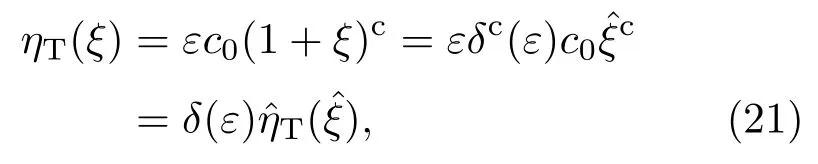
則必須設δ(ε)=εδc(ε), 即

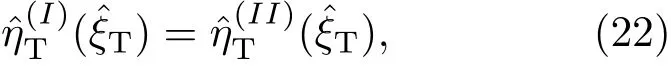
且

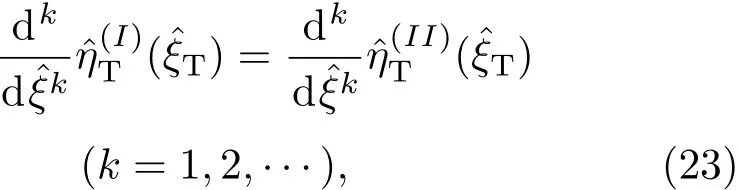
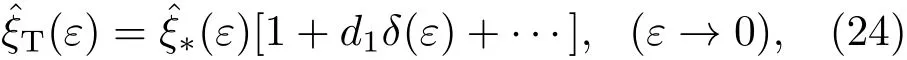
因此,在首級近似中,

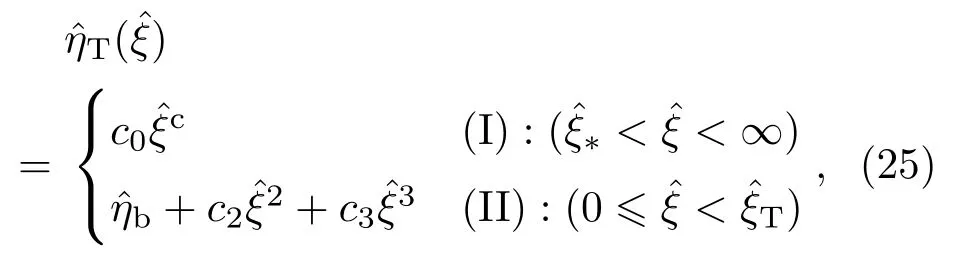
參數

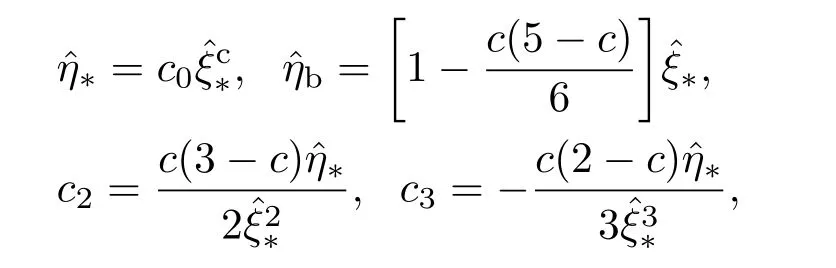
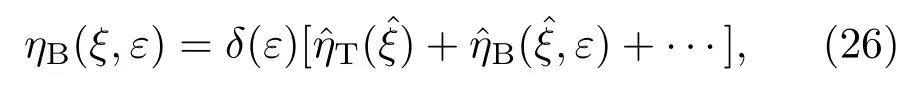
將坐標函數(1)在η→0,ξ→?1做泰勒展開,相應的參數變為

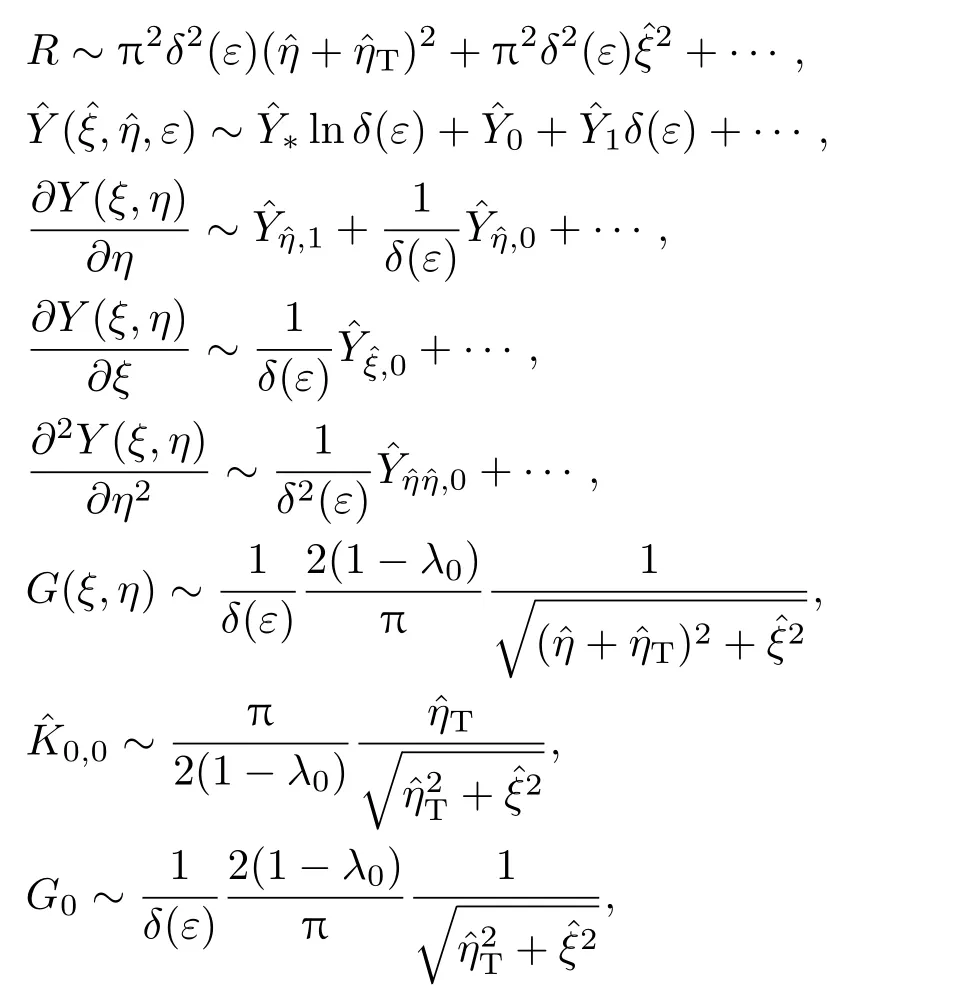
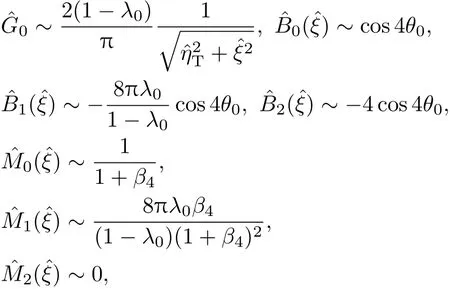
其中

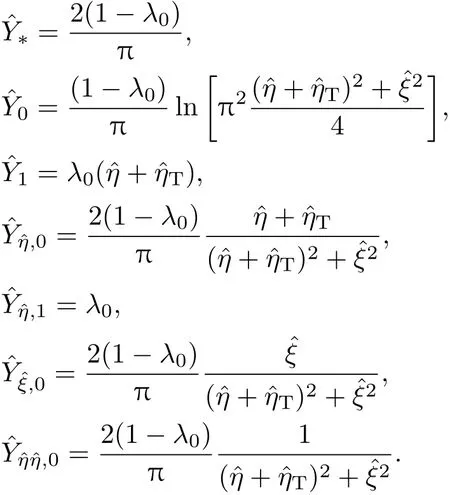
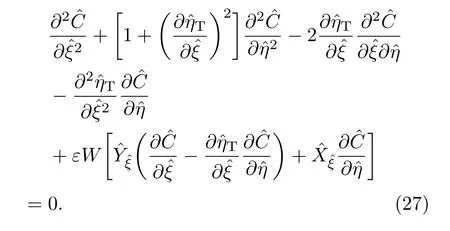
相應的界面條件(8)—(13)變為∶

Gibbs-Thomson條件

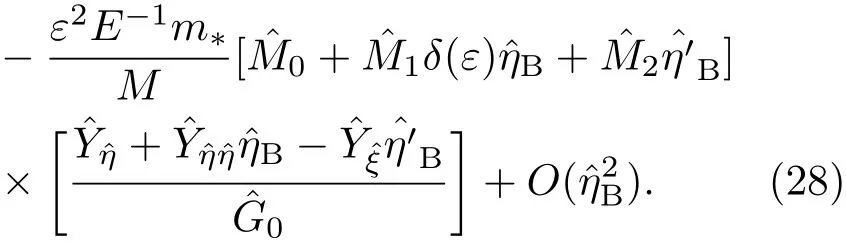
質量守恒條件

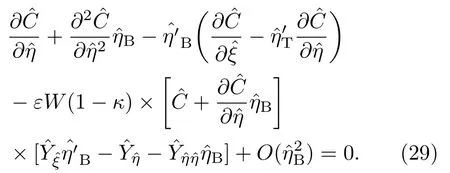
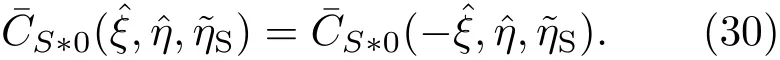
上述非齊次系統(27)—(31)存在如下形式的解[5]∶

運用文獻[5]中的方法可以得到(32)式中非齊次系統的漸近解為

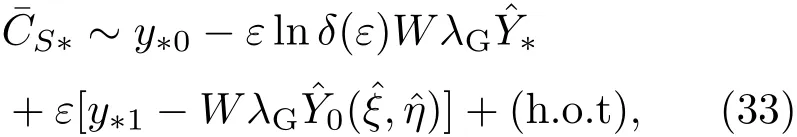
相應的齊次系統的通解為

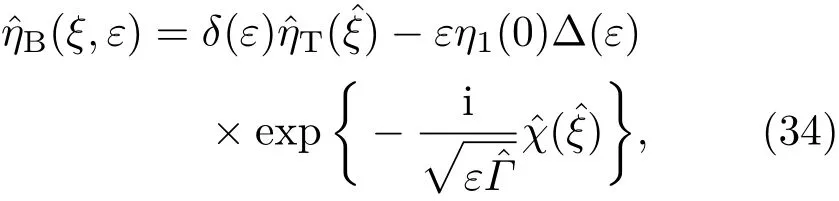
量子化條件為

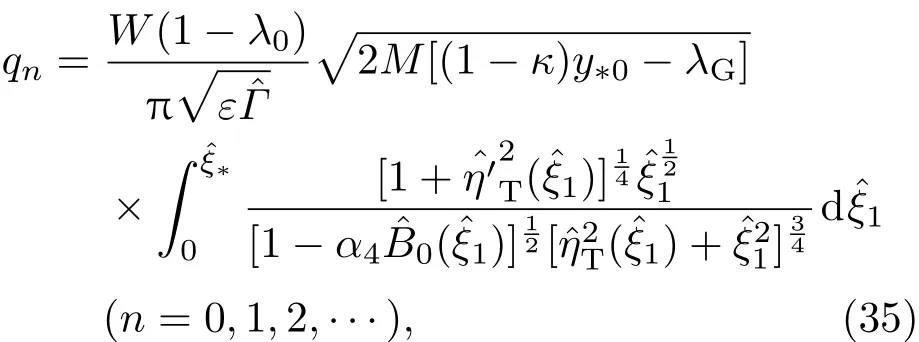
其中

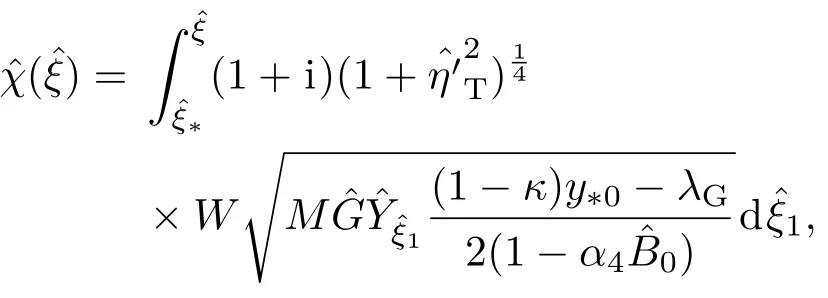
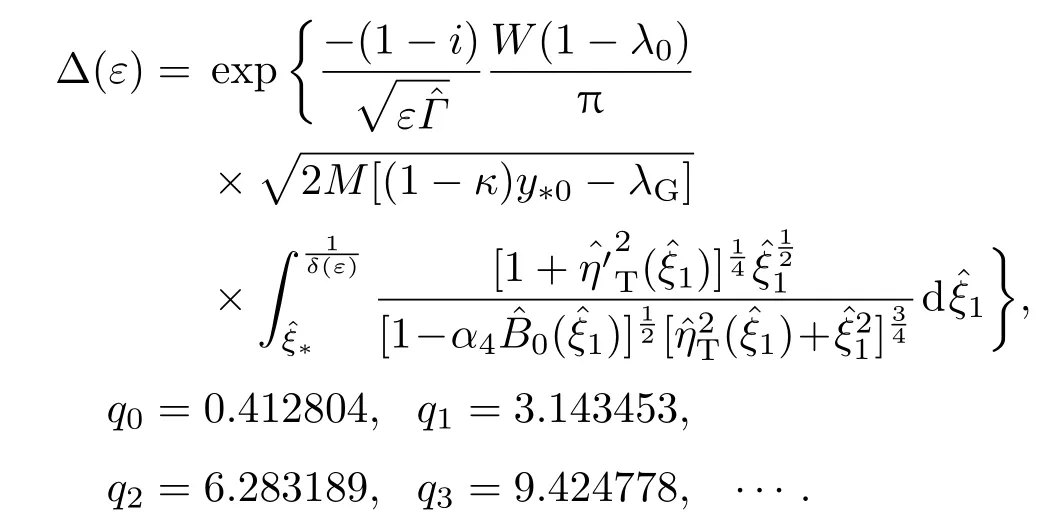
由量子化條件(35)可知,每給定一個qn(n=0,1,2,···),可以解出相應的滿足量子化條件的特征值它們是參數ε和其他參數的函數,并且＜ ···.計算結果表明,特征值隨著n增大而增大,所以只取最小的特征值當q0給定時,可以得到參數ε與其他參數之間的關系,再固定除以外的參數,通過改變參數ε的取值,可以得到參數ε與特征值的關系,即圖1和圖2.從圖1中可以看出,當兩個各向異性偏好方向之間相差的角度θ0為0時,隨著各向異性表面張力系數α4的增大而減小,在低階時與各向異性界面動力學無關.從圖2中可以看出,當0≤ θ0≤ π/4時,隨著θ0的增大而增大;當π/4≤ θ0≤ π/2時,,隨著θ0的增大而減小.

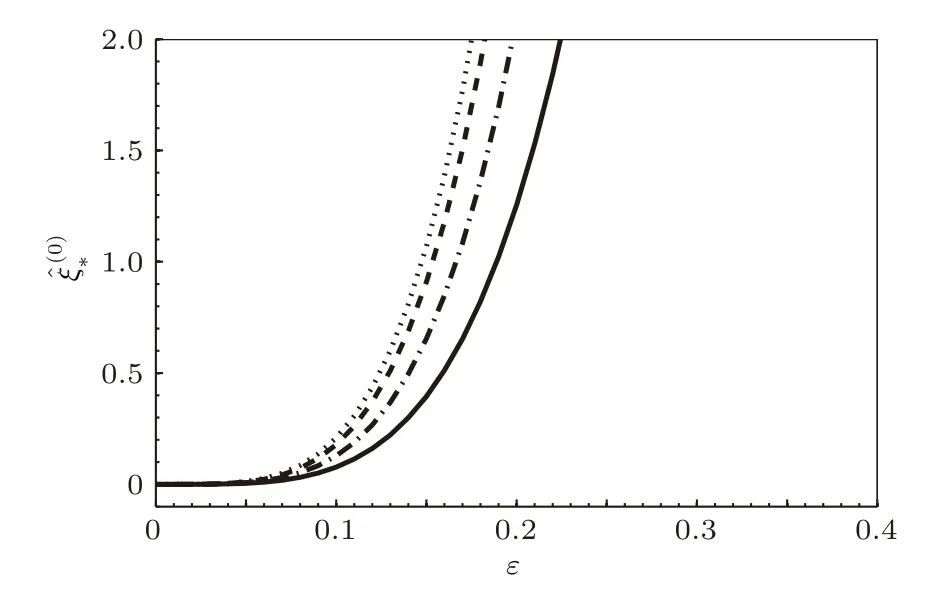
圖1 特征值在不同表面張力系數α4下隨ε的變換 參數取值為κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,=1,θ0=0,曲線從左到右分別對應α4=0,0.01,0.03,0.06Fig.1.The variations ofwith the parameter ε for the cases: κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,=1,θ0=0,and α4=0,0.01,0.03,0.06 from left to right.

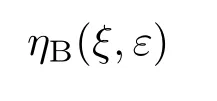
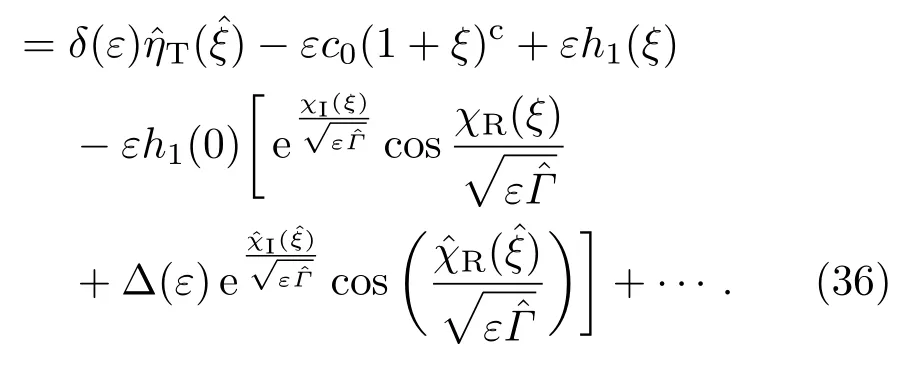
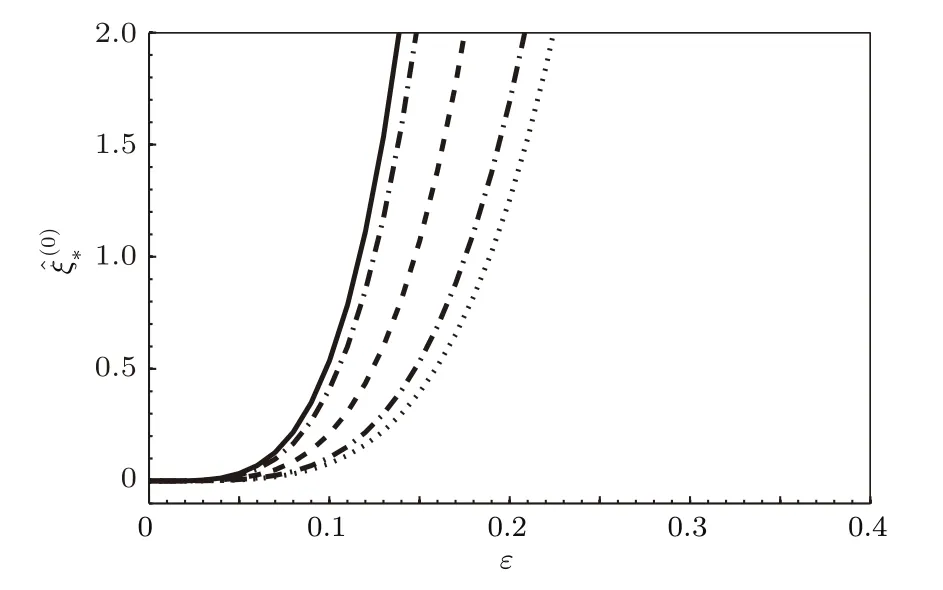
圖2 特征值在不同表面張力系數α4下隨ε的變換 參數取值為κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,=1,α4=0.06,曲線從左到右分別對應Fig.2.The variations ofwith the parameter ε for the cases: κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,=1,α4=0.06,and θ0= left to right.

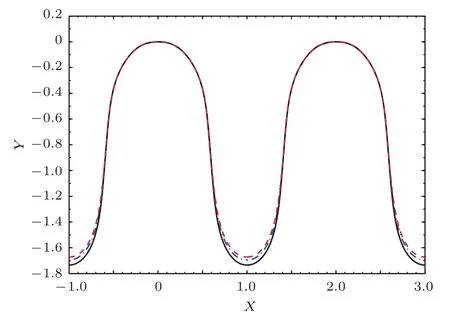
圖3 深胞晶界面形狀合成解函數ηB在(X,Y)平面內的界面形狀 參數取值為κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,E=0.5,=1,m?=1,β4=0.03,θ0=0,從上到下的三條曲線分別對應α4=0.01,0.03,0.06Fig.3.The composite solution for the interface shape function ηBdescribed on(X,Y)plane for the case:κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,E=0.5,=1,m?=1,β4=0.03,θ0=0,and different values of the anisotropic surface-tension coefficient α4=0.01,0.03,0.06 from top to bottom.

由界面形狀的合成解(36)式可知,當參數取值固定時,可以得到深胞晶界面形狀合成解函數ηB在(X,Y)平面內的界面形狀,即圖3、圖4和圖5.從圖3和圖4中可以看出,當兩個各向異性偏好方向之間相差的角度θ0為0時,隨著各向異性系數的增大,深胞晶的指狀界面全長增大,根部底端的曲率半徑會減小,即根部底端的曲率增大,在同一數量級下,各向異性表面張力系數對界面形狀的影響更為顯著.從圖5中可以看出,當0≤θ0≤π/4時,隨著θ0增大,深胞晶的指狀界面全長減小,根部底端的曲率半徑會減小,即根部底端的曲率增大;當π/4≤θ0≤π/2時,隨著θ0增大,深胞晶的指狀界面全長增大,根部底端的曲率半徑會增大,即根部底端的曲率減少.各向異性和角度θ0對深胞晶的總長度和根部均有顯著影響,但在其他固-液界面上,比如深胞晶的頂部,所起的作用并不大.

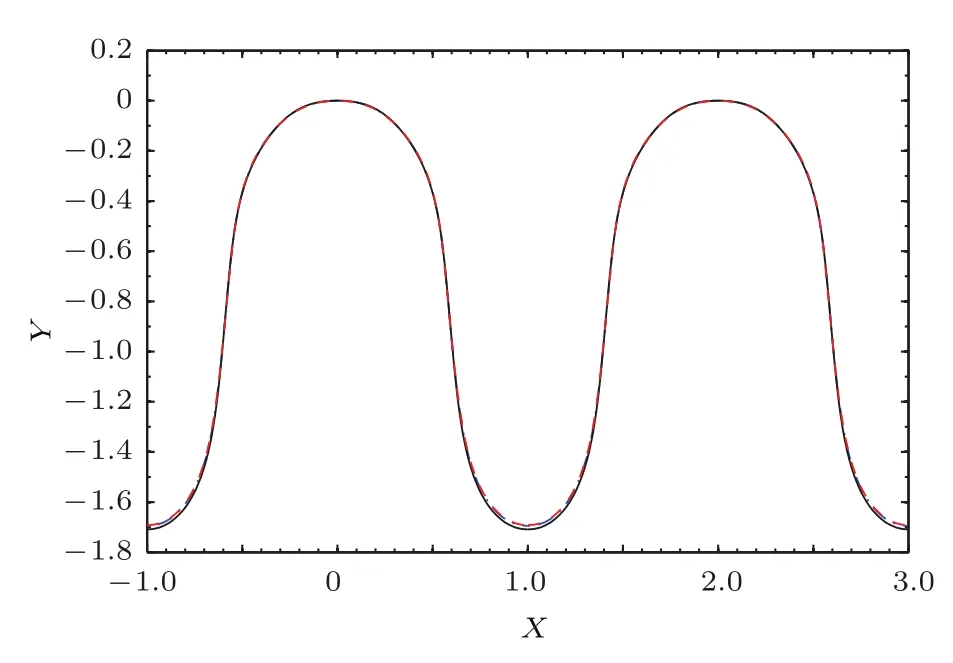
圖4 深胞晶界面形狀合成解函數ηB在(X,Y)平面內的界面形狀 參數取值為κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,E=0.5,=1,m?=1,α4=0.03,θ0=0,從上到下的三條曲線分別對應β4=0.01,0.03,0.06Fig.4.The composite solution for the interface shape function ηBdescribed on(X,Y)plane for the case:κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,E=0.5,=1,m?=1,α4=0.03,θ0=0,and different values of the anisotropic interface kinetics coefficient β4=0.01,0.03,0.06 from top to bottom.

圖5 深胞晶界面形狀合成解函數ηB在(X,Y)平面內的界面形狀 參數取值為κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,E=0.5,=1,m?=1,α4=0.06,β4=0.06,從上到下的五條曲線分別對應θ0=Fig.5.The composite solution for the interface shape function ηBdescribed on(X,Y)plane for the case: κ=0.1,λG=2,λ0=0.6,M=1,c0=2.63,c=0.88,E=0.5,=1,m?=1,α4=0.06,β4=0.06,and differentvalues of the angle θ0=π from top to bottom.

5 結 論

本文應用配漸近展開法和多重變量漸近展開法研究了定向凝固過程中各向異性界面動力學與各向異性表面張力的相互作用對深胞晶生長界面形態的影響,分析了當各向異性界面動力學與各向異性表面張力的偏好方向之間相差角度為θ0時穩定態的特征值問題.結果表明,各向異性界面動力學與各向異性表面張力的偏好方向之間相差的角度會對深胞晶生長形態產生影響.當兩種各向異性偏好方向相同,即θ0為0時,隨著各向異性系數的增大,深胞晶的指狀界面全長增大,根部底端的曲率半徑會減小,即根部底端的曲率增大,且各向異性表面張力系數對深胞晶生長界面形狀的影響更為顯著.當0≤ θ0≤ π/4時,隨著θ0增大,深胞晶的指狀界面全長減小,根部底端的曲率半徑會減小,即根部底端的曲率增大;當π/4≤θ0≤π/2時,隨著θ0增大,深胞晶的指狀界面全長增大,根部底端的曲率半徑會增大,即根部底端的曲率減少.

[1]Ding G L,Huang W D,Lin X,Zhou Y 1997 J.Cryst.Growth 177 281

[2]Ding G L,Lin H,Huang W D,Zhou Y H 1995 Acta Metall.Sin.31 469

[3]Georgelin M,Pocheau A 2006 Phys.Rev.E 73 011604

[4]Georgelin M,Pocheau A 2009 Phys.Rev.E 81 031601

[5]Chen Y Q,Xu J J 2011 Phys.Rev.E 83 041601

[6]Xu J J,Chen Y Q 2015 Eur.J.Appl.Math.26 1

[7]Mullins W W,Sekerka Rf1963 J.Appl.Phys.34 323

[8]Mullins W W,Sekerka Rf1964 J.Appl.Phys.35 444

[9]Saffman P G,Taylor G I 1958 Proc.R.Soc.London A 245 312

[10]Coriell S R,Sekerka Rf1976 J.Cryst.Growth 34 157

[11]Wang Z J,Wang J C,Yang G C 2008 Acta Phys.Sin.57 1246(in Chinese)[王志軍,王錦程,楊根倉 2008物理學報57 1246]

[12]Wang Z J,Wang J C,Yang G C 2010 Chin.Phys.B 19 017305

[13]Trivedi R,Seetharaman V,Eshelman M A 1991 Mater.Trans.A 22 585

[14]Chen M W,Chen Y C,Zhang W L,Liu X M,Wang Z D 2014 Acta Phys.Sin.63 038101(in Chinese)[陳明文,陳奕臣,張文龍,劉秀敏,王自東2014物理學報63 038101]

[15]Jiang H,Chen M W,Shi G D,Wang T,Wang Z D 2016 Mod.Phys.Lett.B 30 1650205

[16]Ihle T 2000 Eur.Phys.J.B 16 337

PACS∶68.70.+w,81.10.Aj,81.30.FbDOI∶10.7498/aps.66.106801

?Corresponding author.E-mail:chenmw@ustb.edu.cn

?Corresponding author.E-mail:wangzd@mater.ustb.edu.cn

Effects of anisotropic interface kinetics and surface tension on deep cellular crystal growth in directional solidification

Jiang Han1)Chen Ming-Wen2)?Wang Tao1)Wang Zi-Dong1)?
1)(Schoolof Materials Science and Engineering,University of Science and Technology Beijing,Beijing 100083,China)
2)(Schoolof Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China)

5 January 2017;revised manuscript

26 February 2017)

In this paper,we study the effects of anisotropic interface kinetics and surface tension on deep cellular crystal growth in directional solidification.The following assumptions are made∶the process of solidification is viewed as a twodimensional problem;the minor species in this binary mixture system is considered as an impurity;the solute diffusion in the solid phase is negligible;the thermodynamic properties other than the diffusivities are the same for both solid and liquid phases;there is no convection in the system;the anisotropic interface kinetics and the anisotropic surface tension are a four-fold symmetry function each;neither the preferred directions of the anisotropic interface kinetics nor the anisotropic surface tensions are necessarily the same as their counterparts for the solid and liquid phases respectively;the angle between the preferred directions of the two anisotropies is θ0.By using the matched asymptotic expansion method and the multiple variable expansion method,we obtain the diagram of interface morphology for a deep cellular crystal in directional solidification.

The results show that there exists a discrete set of the steady-state solutions subject to the quantization condition(35).The quantization condition yields the eigenvalueas a function of parameter ε and other parameters of the system,which determines the interface morphology of the cell.The results also show the variation of the minimum eigenvaluewith parameter ε.It is seen that when the preferred directions of the two anisotropies are the same,i.e.,θ0=0,the minimum eigenvaluereduces with the increase of anisotropic surface-tension coefficient α4,increases with the augment of parameter ε,and is unrelated to anisotropic interface kinetic coefficient β4in the low order;when the angle 0≤ θ0≤ π/4,as the θ0increases,the minimum eigenvalueincreases;when the angle π/4≤ θ0≤ π/2,as the θ0increases,the minimum eigenvaluedecreases.In addition,the results show the composite solution for the interface shape function ηBdescribed on(X,Y)plane.It is seen that both of the anisotropy and the angle θ0have a significant effect on the total length and the root of deep cellular crystal,however,have little influence on the other solid-liquid interface,such as the top of deep cellular crystal.When the angle θ0is 0,as anisotropic coefficient increases,the total length of thefinger increases,the curvature of the interface near the root increases or the curvature radius decreases.It is found that the influence of the anisotropic surface-tension coefficient on interface morphology is more remarkable than that of the anisotropic interface kinetics coefficient.when the angle 0 ≤ θ0≤ π/4,as the θ0increases,the total length of thefinger decreases,the curvature of the interface near the root decreases or the curvature radius increases;when the angle π/4 ≤ θ0≤ π/2,as θ0increases,the total length of thefinger increases,the curvature of the interface near the root increases or the curvature radius decreases.

∶directional solidification,anisotropic surface tension,anisotropic interface kinetics,deep cellular crystal growth

?通信作者.E-mail:chenmw@ustb.edu.cn

?通信作者.E-mail:wangzd@mater.ustb.edu.cn

?2017中國物理學會Chinese Physical Society