顆粒固體應力轉向比的光彈法探測?

宗謹 周志剛 王文廣 張晟 林平 石玉仁 厚美瑛

1)(西北師范大學物理與電子工程學院,蘭州 730070)

2)(中國科學院物理研究所,北京 100190)

3)(中國科學院大學物理學院,北京 100049)

4)(中國科學院近代物理研究所,蘭州 730070)

5)(甘肅民族師范學院物理與水電工程系,合作 747000)

顆粒固體應力轉向比的光彈法探測?

宗謹1)2)5)周志剛2)3)王文廣2)3)張晟4)林平4)石玉仁1)厚美瑛2)3)?

1)(西北師范大學物理與電子工程學院,蘭州 730070)

2)(中國科學院物理研究所,北京 100190)

3)(中國科學院大學物理學院,北京 100049)

4)(中國科學院近代物理研究所,蘭州 730070)

5)(甘肅民族師范學院物理與水電工程系,合作 747000)

(2017年1月19日收到;2017年3月6日收到修改稿)

利用壓敏雙折射光學特性材料,實驗測量了在自然堆積和密堆積兩種制樣方式下顆粒倉軸向荷載在倉壁上隨深度的分布.發現在填充顆粒總質量相同、容器不變的情況下,顆粒倉軸向荷載在倉壁上的分布不隨顆粒深度單調變化,而是隨深度呈單峰結構,數值模擬與實驗觀察定性符合,并且發現峰值依賴于荷載大小和樣品的制備方式.另外,我們也測量了在不同填充高度下的顆粒底部平均應力隨軸向荷載的變化,將其與邊壁應力對比,得到顆粒體系不同深度處的轉向比.

∶顆粒固體,光彈法,轉向比

PACS∶45.70.—n,45.70.CcDOI∶10.7498/aps.66.104501

1 引 言

顆粒物質是由大量離散的固體顆粒所組成的復雜體系,其廣泛存在于我們的日常生活和工業生產中.由于顆粒體系中力的傳遞和分布問題對工業生產、堤壩、建筑等的穩定性至關重要,因此,對顆粒物質的研究近年也引起了物理學家的廣泛興趣[1?3].

靜態堆積的顆粒物質體系,顆粒接觸點分布的隨機性和顆粒間的相互作用力的復雜性和敏感性導致顆粒物質體系中出現了很多異常的特性,如由點源法制備的顆粒堆底部中心出現壓力凹陷[4?6]、糧倉底部的壓力隨倉中顆粒堆積的高度趨于飽和(這在液體中不會出現)等現象[7,8].對于靜態顆粒體系中力的分布特點通過二維光彈顆粒實驗可以清楚地展現[9?12]∶顆粒體系中出現強弱各異的力鏈結構,強力鏈支撐了體系主要的力,其分布呈現出各向異性的特點;而弱力鏈則在顆粒體系中分布較廣泛和均勻.另外,力在靜態堆積的顆粒體系中的傳遞過程也較為特別[13],一些模擬結果表明[14]∶當顆粒體系受到荷載時,離受力點近的距離內,力的傳播很像波;但是在離受力點遠的距離內,力的傳播則導致顆粒物質發生形變.當顆粒間的摩擦力和無序度增大,顆粒體系中力像波一樣傳播的區域將縮小,顆粒間的摩擦力和無序度會增強顆粒體系的彈性模量.

對于常見靜態顆粒體系如糧倉體系,倉中顆粒物質的自重會部分地被分到倉壁承擔,并且隨著倉中顆粒物質的高度增加到底部直徑的2倍以后,倉底感受到的力會趨于穩定.另外,對施加于倉頂的荷載在糧倉中的傳播以及最后倉底承受到的力的分布的實驗[15],發現荷載通過顆粒體系傳遞到倉底的力中大于平均力的部分的分布是指數衰減的,在3D光彈顆粒體系中得到同樣的結果[5],并且進一步的分析發現這和顆粒間的接觸角的分布密切相關.Janssen基于應力的分布特點提出模型對糧倉中的現象進行了解釋,在Janssen模型中[7],假設了顆粒物質的重量按一定比例轉向傳遞到水平方向,并且假設轉向比J為常數.

本文采用光彈片測量了糧倉邊壁法向力隨深度的分布以及糧倉底部的力分布,進而獲得糧倉的轉向比J.我們發現J并不是常數,而是隨顆粒體系的高度而變化的.這說明糧倉體系中的應力張量并非對角化,并且和顆粒的高度相關.

2 實驗裝置

實驗中所用的顆粒倉的內邊壁由光彈片組成,外邊壁由透光性良好、厚度為8 mm的玻璃板構成.在測量前標定光彈片的光強梯度和壓力間的關系,如圖1的定標光路示意圖.光源采用雙激光二極管(LED)面光源組,以45?角對稱入射到光彈片表面,光源中心距離光彈片20 cm,光源前端安放起偏片及1/4波片.光彈片水平置于玻璃板上,在光彈片正下方距光彈片31.5 cm處安置數碼相機(相機像素3664×2748),相機鏡頭前端安放1/4波片及檢偏片,檢偏片與起偏片成90?夾角.定標過程中在光彈片上施加一系列逐漸增大的力,由電荷耦合器(CCD)拍攝對應的光斑.圖2給出壓力=6.7 N時拍攝到的光斑.將光斑圖片進行背景處理后,按(1)式計算[16]圖片中每一個像素點(i,j)的光強梯度平方G2(i,j),如圖3所示.

I(i,j)為像素點的光強,進而按(2)式計算包含整個光斑的區域的平均光強梯度平方∶

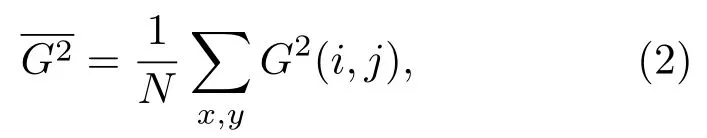
其中N為區域內像素點的數量.

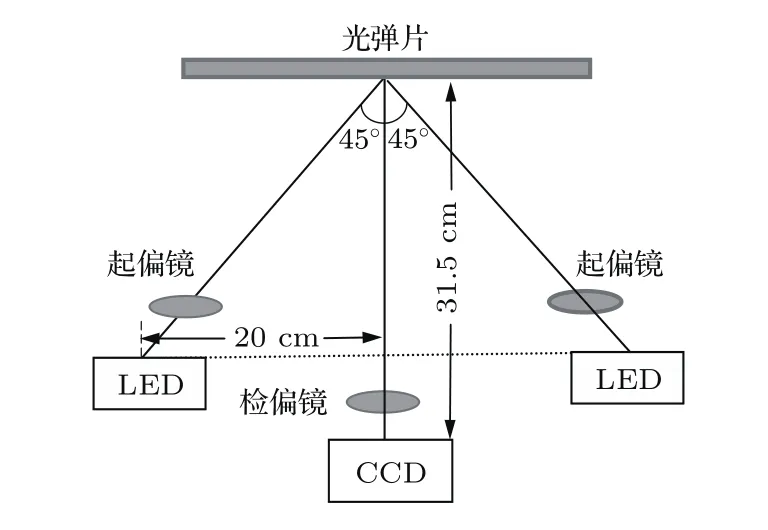
圖1 定標實驗裝置示意圖Fig.1.Setup for calibration.

圖2 拍攝到的光斑Fig.2.The facula shot at the pressed spot.

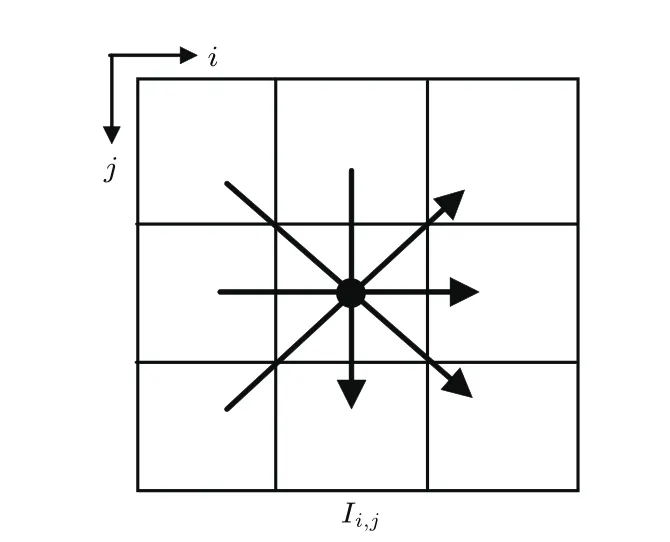
圖3 條紋梯度法說明圖Fig.3.calculation of the gradient of the spot intensity.

圖4 定標曲線Fig.4.The calibration of intensity-gradient vs.force.

定標時所截取的包含光斑區域的大小為160×160像素.圖4得到與光彈片上受力F的關系.通過數據點擬合,近似得到光彈片所受壓力與平均光強梯度平方近似成線性關系∶

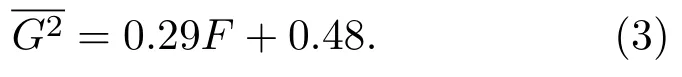
3 實驗結果

3.1 光彈法測量顆粒倉邊壁的正壓力

實際測量顆粒倉邊壁上的壓力分布時,我們選用與定標實驗中完全相同的光源、相機,并且保持光源、相機的位置和定標實驗中相同,如圖5所示.顆粒倉尺寸為6.4 cm×7.4 cm×25 cm.對于制備好的樣品,先拍未受軸向壓時的背景照,然后在顆粒頂部水平放置一厚度為1 mm硬鋁板(與四壁各有0.5 mm間距)用來加軸向壓力(逐次增加砝碼),每次加力均拍攝一次,截取被測面區域3620像素×1160像素(1 mm≈19個像素點),由單位面積內壓敏條紋的平均光強梯度平方來計算側壁的法向壓力.

實驗測量了直徑為4 mm的玻璃珠(顆粒總質量1722 g,密度2.47 g/cm3)在自然堆積和密集堆積情況下,當顆粒樣品軸向施加荷載力時(25—320 N)在容器邊壁上的法向壓力.每張照片在圖像處理時都用未加荷載時的圖片去除背景,從而測量出所加荷載在邊壁上的應力分布情況.

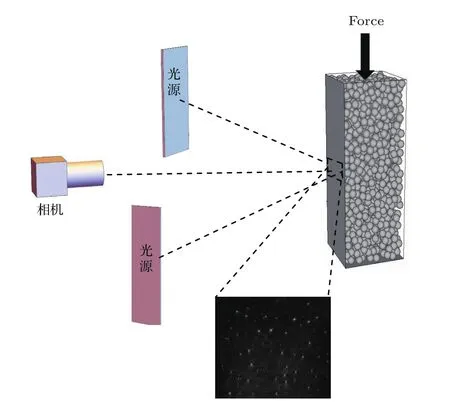
圖5 邊壁應力測量裝置示意圖Fig.5.Schematic of the experimental measurement.

圖6 (網刊彩色)自然堆積法邊壁法向力與深度關系Fig.6.(color online)The normal force at the wall at different height when the sample is prepared by“point-source” method.

圖7 (網刊彩色)密集堆積時邊壁法向力與深度關系Fig.7.(color online)The normal force at the wall at different height when the sample is tapped dense after prepared by “point-source” method.

圖6顯示在自然堆積情況下顆粒堆受軸向荷載時邊壁的法向力隨深度的變化,發現邊壁法向力不隨深度單調增加,成單峰結構.側壁中部受力要大于上部和下部.同時荷載對邊壁的壓力并不是隨著荷載的增加而增加,當荷載增加到260 N時,再增加荷載,荷載對邊壁的壓力整體會減小,原因可能是由少數顆粒組成的強力鏈在較大荷載的作用下斷裂重構,一部分力傳遞到底部.

密集堆積是在點源法堆積制備樣品的基礎上,顆粒頂部施加60 N的荷載,通過敲擊顆粒倉金屬側壁使其密實,然后撤去荷載等待10 min,制得樣品高度22.8 cm,體積分數0.64.軸向荷載通過鋁片加載到樣品頂部,得到圖7所示不同荷載下邊壁應力隨深度的變化關系,可以看出軸向荷載通過顆粒對邊壁施加的法向壓力同樣隨深度成單峰結構,側壁中部受力要大于上部和下部,但是此時邊壁的法向力隨荷載的增加而增加,說明體積分數較大的顆粒體系其強力鏈較為穩定,不容易被破壞.

我們可以看到,無論是自然堆積還是密集堆積,所加荷載較小時,側壁中部受力與下部受力差別較小,隨著荷載的增加,中間部分受力的增幅較上部和下部要大.自然堆積和密集堆積的差異還在于密集堆積顆粒體的剛度較大,能承載的應力較大,在我們加載的荷載范圍內側壁應力呈單調上升,而自然堆積體系則在荷載加到260 N附近側壁應力達到最大.

我們知道顆粒自重隨深度增加,由于Janssen效應,側壁的支撐使得底面示重會線性增加至一個小于實重的飽和值.非單調側壁力分布表明,頂部施加的軸向荷載起到了重要的作用,軸向荷載隨深度增加引起的底部軸向應力σzz以及側壁法向應力σxx與自重的影響趨勢相反,隨深度增加會減小.自重與荷載壓力隨深度變化的相反趨勢是側壁應力非單調分布的主要影響因素.

相同質量的顆粒在密集堆積時,軸向荷載對邊壁的壓力要大于自然堆積時對邊壁的壓力,邊壁應力與顆粒體系的體積分數有關,隨著體積分數的增加,邊壁應力也會增加.

為驗證所觀察到的側壁應力的非單調分布,我們進行了分子動力學數值模擬.模擬是使用運行在GPU上的DEM代碼[17,18]完成的,在該代碼所用的模型中,顆粒之間的作用力由Hertz模型給出[19,20]∶

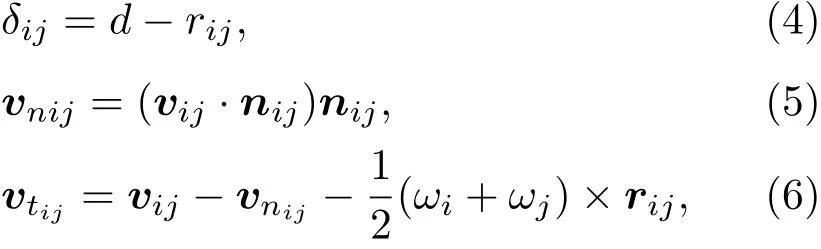
其中r為小球半徑,d為兩小球球心間距,δij為兩個小球的重疊量,ω為角速度,顆粒間的法向和切向接觸力分別為

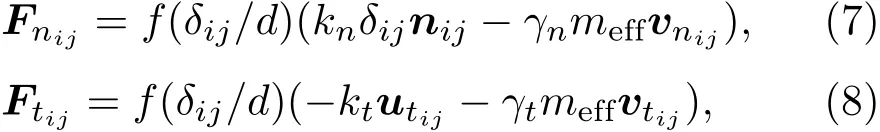
nij是顆粒間位置矢量rij的單位向量;meff為兩接觸顆粒的等效質量;kn,t為彈性系數;rn,t為阻尼系數;vnij是法向相對速度;vtij是切向相對速度.采用庫侖條件|Ftij|≤us|Fnij|對Ftij做了截斷,其中us是顆粒間摩擦系數.顆粒在重力場中的運動方程為

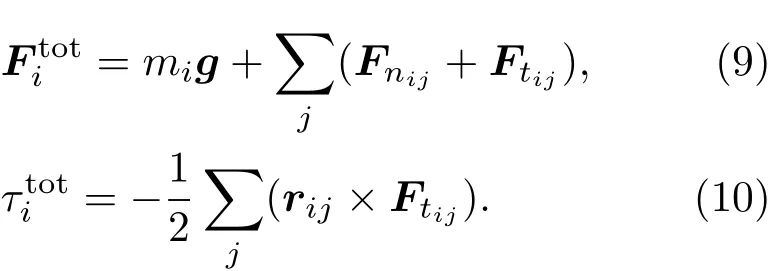
采用Velocity-Verlet方法[21]求解該方程組,實現模擬.模擬中,顆粒采用直徑為1 mm的鋼球,糧倉為圓筒形,直徑為30 mm,高250 mm,在頂部施加45 N的荷載.單一粒徑的鋼球以一個比較小的體積比(0.2)在三維的谷倉中生成,然后在重力的作用下堆積,直到體系的總能量足夠小到可以認為是穩定體系.隨后計算顆粒之間以及顆粒與器壁之間的作用力.模擬所得側壁法向應力σxx隨顆粒深度的變化如圖8所示,與實驗所得圖像變化趨勢定性相同.

圖8 邊壁壓力隨顆粒深度變化的模擬結果Fig.8.The simulated normal force at the side wall at different height.

3.2 顆粒倉底部壓力測量

為了測量糧倉底部的力,在文獻[7,22]中是采用類似天平的裝置直接稱量的方法.如圖9,我們將一尺寸為6.4 cm×7.4 cm×25 cm的長方體糧倉固定在鋼架上,糧倉底部和邊壁分離,底部用一厚度為1 mm的硬鋁片,鋁片四周與倉壁各有0.5 mm的間隙,通過一圓柱體將顆粒視在質量傳遞到精度為0.1 g,量程為30 kg的電子秤上,選用顆粒直徑4 mm的玻璃珠.顆粒頂部水平放置與底部相同的鋁片,用來加載荷載.由于每次加載顆粒或增加荷載,電子秤示數都會有一定的波動,所以測量時每次讀數均為電子秤達到穩定時的示數.

圖9 底部壓力測量裝置示意圖Fig.9.Schematic of the sample weight measurement by balance.

3.2.1 底部示重隨顆粒高度的變化

測量糧倉底部示重的實驗是采用點源法制備顆粒樣品∶將顆粒注入到漏斗中,漏斗口距離顆粒倉底部239 mm,漏斗口直徑20 mm,漏斗口處于顆粒倉豎直方向正上方的中心位置,顆粒物質通過漏斗口注入顆粒倉.記錄顆粒高度、顆粒實重及顆粒倉底部受力的數據,實驗結果見圖1,黑點為所添加顆粒的實際重量,紅點為測量到的示重.從圖10可以看出,顆粒倉底部示重出現了飽和趨勢.

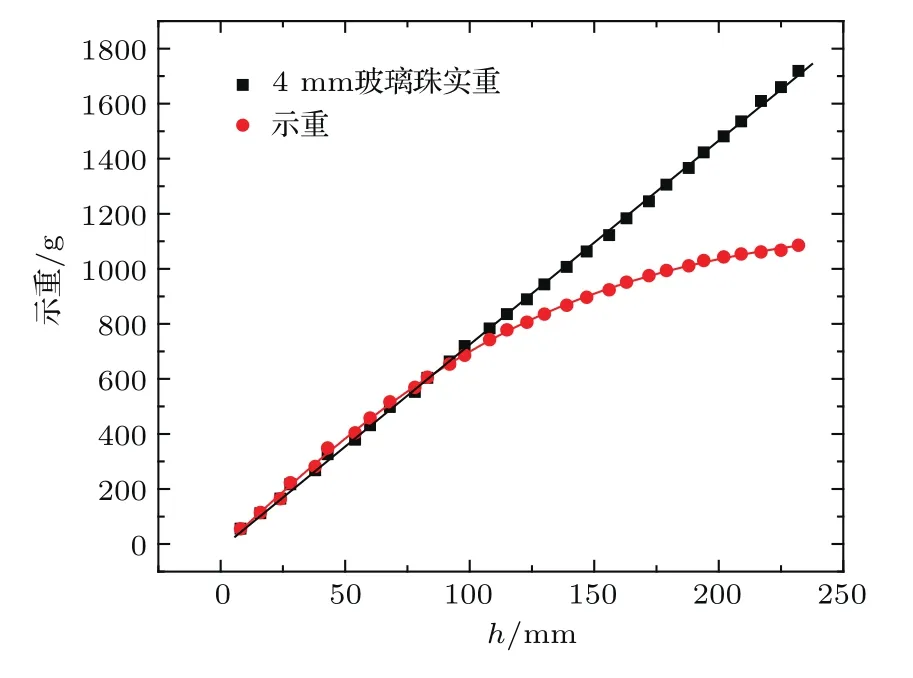
圖10 底部示重隨顆粒高度變化Fig.10.The apparent weight measured as a function of height.

我們采用Janssen公式[22]對顆粒倉底部示重數據點進行擬合,

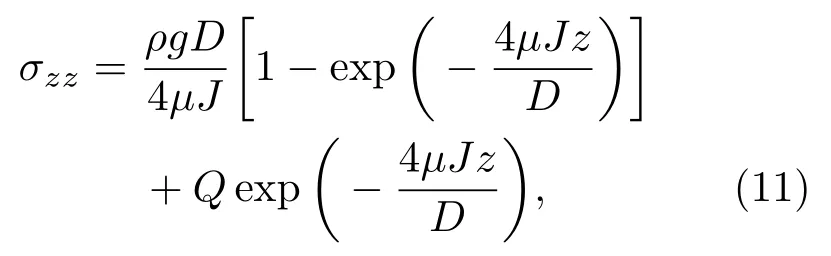
其中g為重力加速度,ρ為顆粒質量密度,D為顆粒倉直徑,μ為顆粒與倉壁的摩擦因數,J為轉向比,Z為顆粒深度,Q為糧倉軸向荷載.在圖10中取Q=0,可擬合得到紅色實線(示重曲線),根據實驗參數和擬合公式可計算出μJ=0.1(μ為顆粒與倉壁的摩擦因數,J為轉向比).這和文獻[7,22]中被假設成常數的值相比稍微偏小,近些年的實驗結果[23,24]發現μJ并不是材料的參數,受糧倉邊壁的變形,糧倉壁摩擦是否被充分動員等因素的影響.

3.2.2 底部示重隨所加荷載變化

為測量軸向壓σzz,利用測量密集堆積邊壁應力隨深度變化時相同的制樣方式敲擊顆粒倉金屬壁使顆粒密實,在樣品頂部水平放置一厚度為1 mm,四周與倉壁間距0.5 mm的硬鋁片,在鋁片上施加軸向荷載,測量底部示重隨荷載的變化,為了研究頂部荷載傳遞到底部的示重,在處理數據時,對每個數據點都減去了無荷載時顆粒體系本身所產生的示重.實驗中不同高度的顆粒都是將顆粒倉中已有顆粒全部倒出后重新制樣,得到的實驗結果見圖11.

不論顆粒堆積高度為多少,底部示重隨荷載都按線性關系變化,但是不同的顆粒堆積高度,示重隨荷載變化的斜率不同.底部示重隨荷載變化的斜率隨顆粒高度按負指數形式變化,根據Janssen公式(11),當顆粒高度一定,底部示重隨軸向荷載按線性關系變化,其線性變化的斜率為

采用(12)式擬合所得曲線見圖11中的插圖.從插圖中可以看出,顆粒高度越大,斜率越小,也就是說相同的荷載,若顆粒倉中的顆粒高度越大,其荷載本身傳遞到底部的壓力將越小.當顆粒深度一定時,在顆粒頂部施加軸向荷載Q,底部壓力隨荷載線性變化的斜率滿足K=exp(?4μJz/D).根據實驗參數和(12)式我們計算出此種情況下的μJ=0.11.

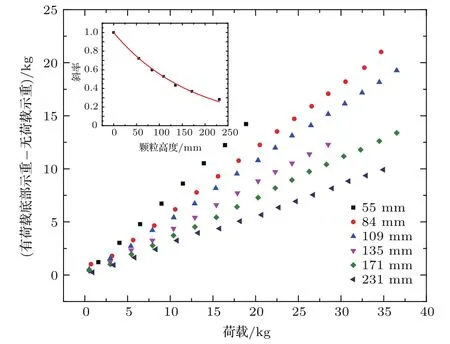
圖11 (網刊彩色)減去無荷載示重的底部示重隨軸向荷載變化曲線(插圖為減去無荷載示重的底部示重隨荷載變化的斜率和顆粒高度的關系)Fig.11.(color online)The apparent weight vs.the load for differentfilling heights.Inset:The slope of the weight against the load as a function of thefilling height.

4 轉向比

利用光彈法,我們測量了密堆積顆粒體系在軸向荷載下任一高度處對顆粒倉邊壁的壓力,將所測邊壁應力除以所對應面積作為該深度處側壁的平均壓強σxx(對應某一高度處的面積為0.5 cm×7.4 cm);直接測量顆粒體系內部任意深度處的應力而不對體系產生影響是不容易的,這里我們根據上述測量軸向荷載在不同高度顆粒體系底部的壓力結果和Janssen公式符合,在假設Janssen公式對顆粒體系內部應力也適用時,結合實驗中的參數和Janssen公式可以推算得到顆粒密堆積時任一深度處底部應力隨荷載變化的斜率,再乘以對應軸向荷載作為該深度處的軸向力,假設同一個水平面內軸向力的分布是均勻的,將計算所得軸向應力除以面積(7.4 cm×6.4 cm)作為該深度處的壓強σzz,根據轉向比的定義J=σxx/σzz,便可計算出不同荷載作用下不同深度處的轉向比.由于靠近邊壁處顆粒的排布和顆粒體系內部顆粒間的接觸結構往往不同,這里獲得任意深度處的軸向應力的方法還比較粗略,通過在邊壁上固定一層顆粒作為邊壁,這樣在一定程度上能使顆粒體系內部的顆粒接觸特點和在邊壁上的類似.

圖12給出了實驗得到的轉向比,可以看出,對于密堆積顆粒體系中軸向荷載沿深度的分布并不是均勻的,轉向比不是一個常數,隨深度呈現出單峰結構.荷載較小時,同一深度處的轉向比隨荷載的增大而減小,當荷載超過150 N時,轉向比受荷載影響較小.

在上述討論顆粒倉底部應力隨顆粒高度以及軸向荷載變化時也提到,μJ是和裝置、顆粒樣品制備歷史等都相關,所以圖12中計算J仍有這些因素的影響,只能通過更精細的實驗進一步改進實驗結果的精度.

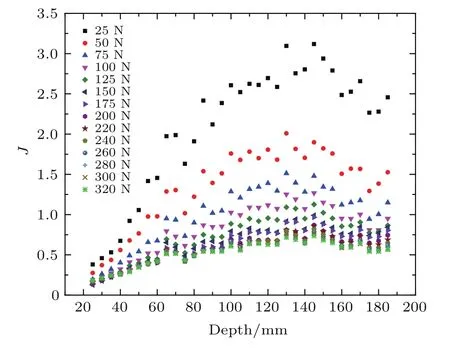
圖12 (網刊彩色)轉向比隨深度變化Fig.12.(color online)Janssen ratio vs.depth.

5 結 論

通過光彈實驗和數值模擬,研究了軸向荷載在顆粒倉邊壁上隨顆粒深度的分布.我們發現隨著深度的增加,倉壁上力的分布呈單峰結構,并且峰值的大小與荷載、樣品的體積分數等因素相關.在相同軸向荷載條件下,密堆積顆粒體系邊壁上的力比自然堆積的大.在相同堆積顆粒體系中,軸向荷載在顆粒倉邊壁中部附近的增幅隨軸向荷載的增加比倉壁底部的增幅要大,顆粒倉最容易出現破壞的位置在中部而不是倉體的底部.在顆粒填充量一定時,顆粒倉底部受力隨荷載的增加呈線性增加,其斜率隨顆粒高度的增加按負指數形式衰減.另外,軸向荷載作用下顆粒倉中的轉向比并不是一個常數,其值與顆粒深度及荷載大小等因素有關.

[1]Jaeger H M,Nagel S R,Behringer R P 1996 Rev.Mod.Phys.68 1259

[2]de Gennes P G 1992 Rev.Mod.Phys.64 645

[3]Liu A J,Nagel S R 1998 Nature 396 21

[4]Zuriguel I,Mullin T,Arévalo R 2008 Phys.Rev.E 77 1006

[5]Liu C H,Nagel S R,Schecter D A,Coppersmith S N,Majumdar S,Narayan O,Witten T 1995 Science 269 513

[6]Geng J,Longhi E,Behringer R P,Howell D W 2002 Phys.Rev.E 64 060301

[7]Janssen H A 1896 Civ.Inst.Eng.Proc.124 553

[8]Sperl M 2006 Granular Matter 8 59

[9]Vitelli V,van Hecke M 2011 Nature 480 325

[10]Bi D P,Zhang J,Chakraborty B,Behringer R P 2011 Nature 480 355

[11]Wambaugh J F,Hartley R R,Behringer R P 2010 Eur.Phys.J.E 32 135

[12]Hartley R R,Behringer R P 2003 Nature 421 928

[13]Luding S 2005 Nature 435 159

[14]Goldenberg C,Goldhirsch I 2005 Nature 435 188

[15]Corwin E I,Jaeger H M,Nagel S R 2005 Nature 435 1075

[16]Hartley R R 2003 Ph.D.Dissertation(USA:Duke University)

[17]Tian Y,Qi J,Lai J,Zhou Q 2013 International Joint Conference on IEEE Nov.2–4,2013 p547

[18]Qi J,Li K C,Jiang H,Zhou Q,Yang L 2015 Int.J.Comput.Sci.Engineer.11 p330

[19]Silbert L E,Ertas D,Grest G S,Halsey T C,Levine D 2002 Phys.Rev.E 65 031304

[20]Silbert L E,Ertas D,Grest G S,Halsey T C,Levine D,Plimption S J 2001 Phys.Rev.E 64 051302

[21]Allen M P,Tildesley D J 1989 Computer Simulation of Liquids(Oxford:Oxford University Press)

[22]Sperl M 2006 Granular Matter 8 59

[23]Li Z F,Peng Z,Jiang Y M 2014 Acta Phys.Sin.63 104503(in Chinese)[李智峰,彭政,蔣亦民2014物理學報63 104503]

[24]Jiang Y M,Zheng H P 2008 Acta Phys.Sin.57 7360(in Chinese)[蔣亦民,鄭鶴鵬 2008物理學報 57 7360]

PACS∶45.70.—n,45.70.CcDOI∶10.7498/aps.66.104501

*Project supported by the National Natural Science Foundation of China(Grant Nos.11274354,11474326,11565021),the“Strategic Priority Research Program-SJ-10” of the Chinese Academy of Sciences(Grant No.XDA04020200),and the Special Fund for Earthquake Research of China(Grant No.201208011).

?Corresponding author.E-mail:mayhou@iphy.ac.cn

Janssen ratio in granular solid measured by photoelastic method?

Zong Jin1)2)5)Zhou Zhi-Gang2)3)Wang Wen-Guang2)3)Zhang Sheng4)Lin Ping4)Shi Yu-Ren1)Hou Mei-Ying2)3)?
1)(Northwest Normal University,Lanzhou 730070,China)
2)(Key Laboratory of Soft Matter Physics,Beijing National Laboratory for Condense Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China)
3)(College of Physics,University of Chinese Academic of Sciences,Beijing 100049,China)
4)(Institute of Modern Physics,Chinese Academy of Sciences,Lanzhou 730070,China)
5)(College of Physics and Hydropower Engineering,Gansu Normal University For Nationalities,Hezuo 747000,China)

19 January 2017;revised manuscript

6 March 2017)

In this work Janssen ratio is measured in a dense granular pack.The pressure on the side walls as a function of the depth of the pack with top load under gravity is measured by photoelastic method.The samples are prepared by“point source”method with and without tapping.A non-monotonic distribution of the side pressure along the depth is found.Numerical simulation is performed and shows qualitative consistency with the experimentalfinding.The apparent weight of the sample is measured for differentfilling heights and for different top loads.Comparing with the normal stresses on the silo wall for different heights,we obtain the Janssen ratio J=σxx/σzzas a function of height.Wefind that although uJ=0.11 is a constant as is expected,the Janssen Ratio is height dependent.It becomes height independent only when the top load is large enough.

∶granular solid,photoelastic method,Janssen ratio

?國家自然科學基金(批準號:11274354,11474326,11565021)、中國科學院空間科學戰略性先導科技專項(批準號:XDA04020200)和地震行業科研經費(批準號:201208011)資助的課題.

?通信作者.E-mail:mayhou@iphy.ac.cn

?2017中國物理學會Chinese Physical Society