缺陷致非線性電路孤子非對稱傳輸?

劉昊華 王少華 李波波 李樺林

(南京大學聲學研究所,近代聲學教育部重點實驗室,南京 210093)

缺陷致非線性電路孤子非對稱傳輸?

劉昊華 王少華?李波波 李樺林

(南京大學聲學研究所,近代聲學教育部重點實驗室,南京 210093)

(2016年11月8日收到;2017年3月2日收到修改稿)

設計了一種有缺陷的非線性電感-電容(LC)電路,簡單方便地實現了電路能量非對稱傳輸,且其能量的載體是非線性波——孤子.在LC電路中,當缺陷靠近驅動時,驅動頻率接近缺陷本振頻率,缺陷共振致電路導通.遠離驅動時,電路不導通.缺陷的引入改變電路的均一性,實現小驅動振幅下孤子的單向釋放,提高驅動能量轉化為孤子能量的效率.對非線性LC電路的傳輸能量、缺陷系數和驅動振幅三者的關系進行了討論.

∶缺陷,非線性電路,孤子,能量

PACS∶05.45.Yv,43.25.RqDOI∶10.7498/aps.66.100502

1 引 言

半導體二極管的出現給我們的社會和生活帶來了巨大改變.電子二極管能很好地實現能量整流和能量非對稱傳輸.其中,能量非對稱傳輸是指能量只能沿特定方向傳播,反向則被阻止.受此啟發,人們開始關注和研究其他領域內的能量非對稱傳輸現象[1?7].在聲學方面,Li等[1]通過聲子晶體的非對稱排布,打破空間反演對稱性實現單向聲傳播.Liang等[2]采用耦合超晶格和強非線性煤質的方式,制備了聲二極管.在熱傳導方面,Li等[3]用兩條耦合的非線性晶格鏈建立了熱二極管模型,Hu等[4]進一步探討了非線性晶格鏈中耦合強度對非對稱熱傳導的影響.在光學方面,Konotop和Kuzmiak[5]利用兩種雙層光子晶體的組合,實現了光的單向傳播.然而據我們所知,目前僅有陳偉中課題組[8,9]對非線性電感-電容(LC)電路中的能量不對稱傳播現象進行了研究,但是在小驅動電壓振幅下電路單向導通能量的效率低,甚至不導通.另外,自Hirota和Suzuki[10]采用非線性LC電路模擬Toda晶格鏈之后,所得研究結果受到了高度重視.這主要是因為非線性LC電路為研究非線性色散媒質中的波傳輸現象提供了一種簡單而又有效的途徑.同時,非線性LC電路在能量和能流的測量方面具有獨特的優勢,如電壓和電流可通過數字示波器和電流表直接測量并記錄分析,而且其電路容易實現,電子器件便于更換和調整.非線性LC電路支持著孤子的存在[11?14],且孤子通信具有容量大、誤碼率低、抗干擾能力強、不用中繼站等特點[15],因此如何高效方便地實現電路中孤子非對稱傳輸具有重要意義.針對此目標,本文以非線性LC電路為研究對象,通過引入缺陷(電容缺陷及電容電感缺陷)的方式[16],實現LC電路中的孤子非對稱傳輸.依托非線性LC電路的系統微分方程組,對系統禁帶內的能量流動進行了詳盡的分析.本方案具有結構簡單、功耗低、孤子能量轉換效率高等優點,且不同于Tao等[8]的耦合非線性電路方式和Liu等[17]的變振幅方法.

2 理論模型

本文采用標準的非線性LC電路,其基本元件包括線性電感L和非線性電容C(Vn),如圖1所示.非線性電容的實現采用反向偏置二極管BB112的方式,偏置電壓Vb=2 V,非線性電容容值與其兩端電壓關系的二階泰勒形式為[18]

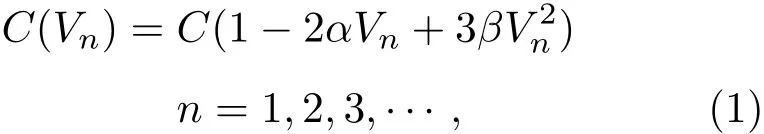
其中C=320 pF,α=0.21 V?1,β=0.0197 V?2.

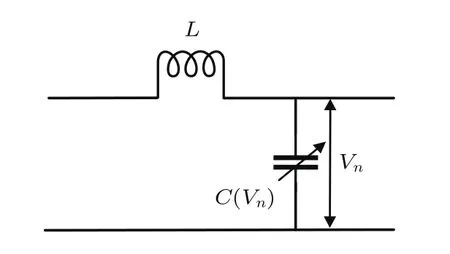
圖1 系統的單元結構Fig.1.A unit of the system.

對圖1單元結構組成的電路系統,應用基爾霍夫定律,得到系統的非線性微分方程組∶

由基礎解exp[i(kn?wt)],得到該周期系統典型的線性色散關系式∶

其中wc是系統的截止角頻率,w是驅動角頻率,k是傳播波數.歸一化驅動角頻率wN=w/wc和傳播波數k的曲線關系見圖2.

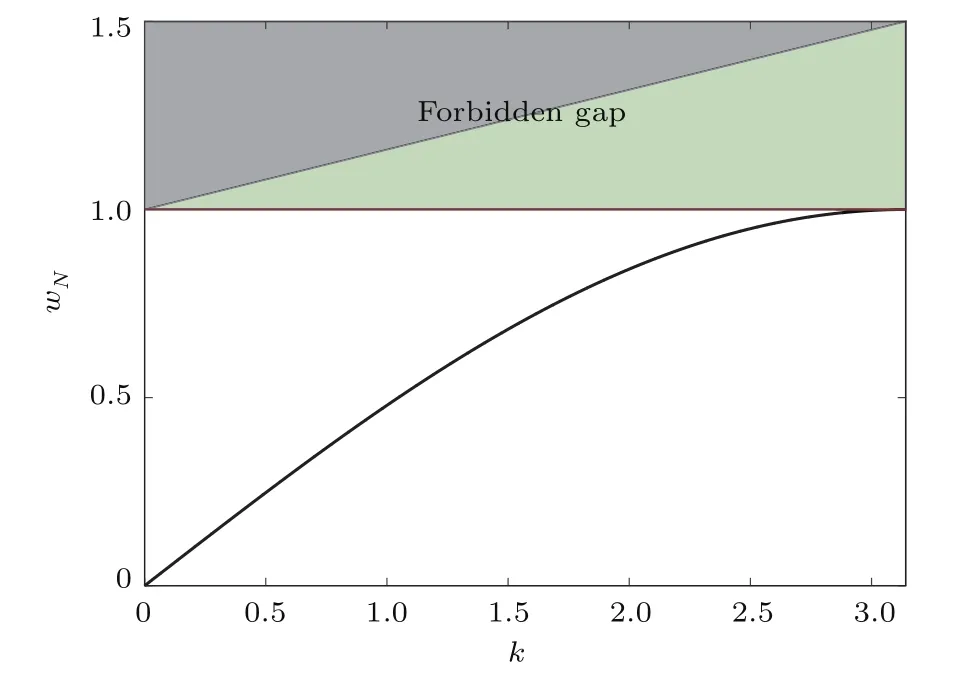
圖2 非線性LC電路的線性色散曲線Fig.2.Linear dispersion curve of the nonlinear LC line.

如圖2所示,我們關注的是系統在禁帶(forbidden gap)內的非線性行為.已有研究表明非線性LC電路在禁帶內存在電壓閾值[19]∶

當驅動電壓V=V0cos(wt),且驅動振幅V0＞Vth,w＞wc時,驅動激發的漸消波失穩,進入不穩定狀態,導致有包絡孤子產生并傳播.

本文主要研究非線性LC電路第一個單元結構中引入線性缺陷所誘導的非對稱孤子傳輸現象.按固體物理的理論,均勻晶格中的缺陷會產生局域在缺陷附近的高頻振動,稱為局域波.當缺陷是第一個電容(CI)時,其本征頻率為[20]

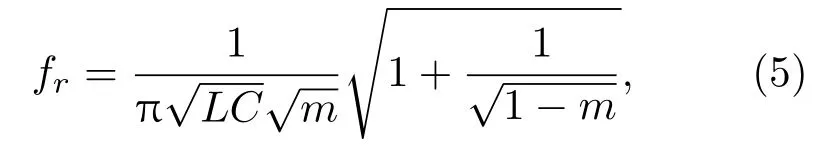
其中m是缺陷系數,定義為m=CI/C.缺陷引起的局域化的波是一種本征束縛態模式,它以本征頻率fr振動.在線性狀態下,局域波的能量不會輻射掉,因為其本征頻率fr在系統線性波的禁帶之內.但當外界驅動靠近缺陷且驅動頻率接近線性本征頻率fr時,局域的振動模式將會進入非線性共振態,進而引起局域波動模式的不穩定,從而導致包絡孤子的發射.由于局域共振的特點,很小的驅動振幅就可以使得局域化模式被共振放大,當儲存在局域化模式的能量足夠大時,局域波動能量幾乎全部轉換為行波孤子能量.當外界驅動遠離缺陷,小驅動振幅不能發射孤子.

3 數值模擬

本文討論兩種缺陷形式,電容缺陷和電容電感缺陷.

3.1 電容缺陷

如圖3所示,電容缺陷處于第一個單元的位置,緊鄰A端.以缺陷系數m=0.7為例,由(5)式得缺陷處的本征頻率fr=1.2052 MHz.仿真中取1200個單元結構,電感L=220μH,非線性電容如(1)式.驅動電壓V=V0cos(wt),V0=0.15 V,w=2πf.由上述參數,該系統的線性截止頻率fc=1.1997 MHz,而關注的是系統在禁帶之內的非線性行為,且驅動頻率f靠近缺陷處的本征頻率fr,因此選取f=1.2 MHz.分別置驅動于A,B端,觀察電路中電壓值的分布和變化情況.利用四階龍格-庫塔計算方法對系統非線性微分方程組(2)進行積分運算.積分時間t=3 ms.驅動振幅V0由零逐漸增長到最大值,防止初始沖擊帶來錯誤的仿真結果.圖4展示了時間t=2.5 ms、分別從A,B端驅動時電路系統內的波形.可清楚地看到,從電路系統的A端驅動,系統內會有能量流動,而且能量的載體是包絡孤子.進一步的數值模擬發現,隨著模擬時間的延長,孤子傳播的距離也越遠.而從B端驅動,系統的能量基本局限在表面,能量無法遠距離傳輸.圖5給出了離驅動的第90個非線性電容兩端電壓隨時間變化的波形圖.觀察到,A端驅動,有孤子電壓信號通過第90個非線性電容,1.25 ms之前是孤子的產生和傳播的過程;B端驅動,沒有孤子信號通過第90個電容,并且幾乎沒有能量通過.由(4)式,得到Vth=0.37 V.雖然數值仿真的驅動振幅V0＜Vth,但A端驅動,即缺陷靠近驅動時,缺陷共振[21]會向驅動吸收大量能量并且存儲,存儲到一定程度會釋放能量,產生傳播孤子,電路導通.B端驅動時,缺陷遠離驅動(本文中缺陷離B端驅動接近1200個單元),能量傳輸指數衰減,缺陷幾乎不能從驅動吸收到能量,更達不到能量積攢,因此電路不導通.缺陷靠近驅動源時,缺陷共振吸收驅動能量的能力遠大于沒有缺陷的電路,可實現小振幅釋放孤子的目的,提高了非線性LC電路釋放孤子的效率.

圖3 電容缺陷Fig.3.Capacitance impurity.

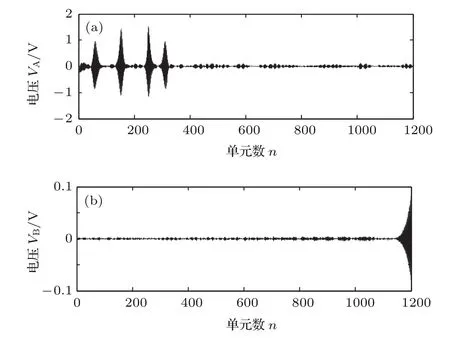
圖4 m=0.7、t=2.5 ms、分別從A,B端驅動時電路系統內的波形(驅動振幅V0=0.15 V,頻率f=1.2 MHz)Fig.4.Emulation oscillograms at t=2.5 ms and m=0.7 of the electrical line which is drived from A and B respectively for a driving frequency of 1.2 MHz and amplitude of 0.15 V.

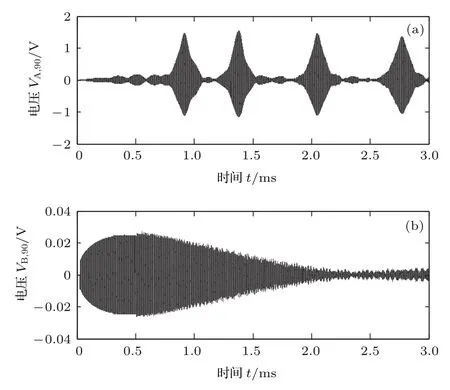
圖5 離驅動的第90個非線性電容兩端電壓V隨時間t的變化Fig.5.The time domain waveforms of voltage V and time t of the nonlinear capacitance which is the 90th away from driver.

3.2 相關性參數分析

電容缺陷下,進一步研究LC電路傳輸能量、缺陷系數和驅動振幅三者的關系.通過離驅動的第i個電容歸一化能量定義為[19]

3.2.1 缺陷系數

驅動振幅一定時(以V0=0.15 V為例),圖6給出了離驅動的第90個電容歸一化能量Ej,90(j=A,B)和缺陷m的關系.這個位置離驅動端足夠遠,從而可以忽略漸消波和局域化波對平均能流的影響.觀察到A端驅動,缺陷系數0.6＜m＜0.9,EA,90會出現陡增,此時系統會產生能量超傳輸現象,數值模擬表明能量的載體是包絡孤子.B端驅動時,EB,90都很小 (注意圖6(b)的縱坐標量級10?5),這說明系統基本沒有能量傳輸.驅動振幅一定,選擇合適的缺陷,可實現孤子非對稱傳輸.

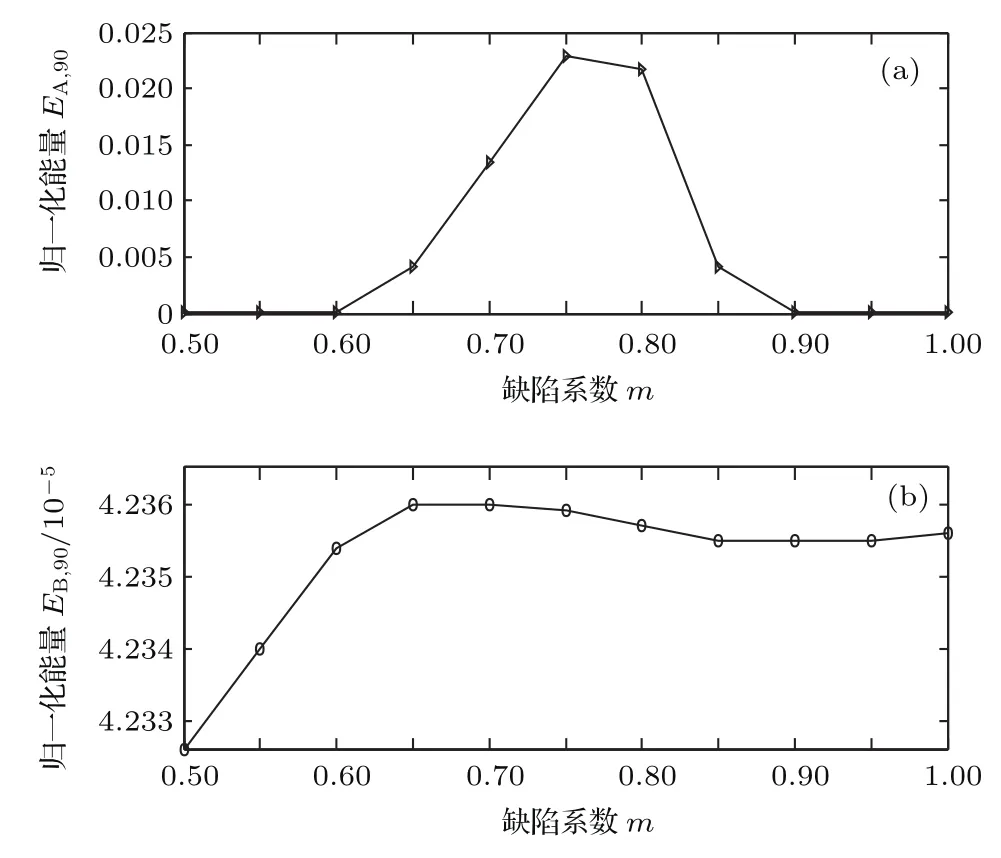
圖6 離驅動的第90個電容歸一化能量和缺陷的關系(驅動振幅V0=0.15 V,頻率f=1.2 MHz)Fig.6.The relation of normalized energy and impurity of the corresponding 90th nonlinear capacitances for a driving frequency of 1.2 MHz and amplitude of 0.15 V.

3.2.2 驅動振幅

缺陷系數一定時,驅動振幅對于實現LC電路孤子非對稱傳輸非常重要.B端驅動,驅動振幅V0＜Vth時,由于缺陷遠離驅動(本文中缺陷離B端驅動接近1200個單元),非線性LC電路系統不能實現能量遠距離傳輸.圖7是A端驅動、不同缺陷下通過第90個非線性電容的能量和驅動振幅的關系.我們發現,每種缺陷下,小于某個驅動振幅值,傳輸能量都很小,超過該值,傳輸能量會出現陡增現象,此時LC電路產生傳播孤子.進一步,隨著模擬時間的延長,孤子會繼續傳播.據此,實現孤子的可控單向激發,即孤子非對稱傳輸.

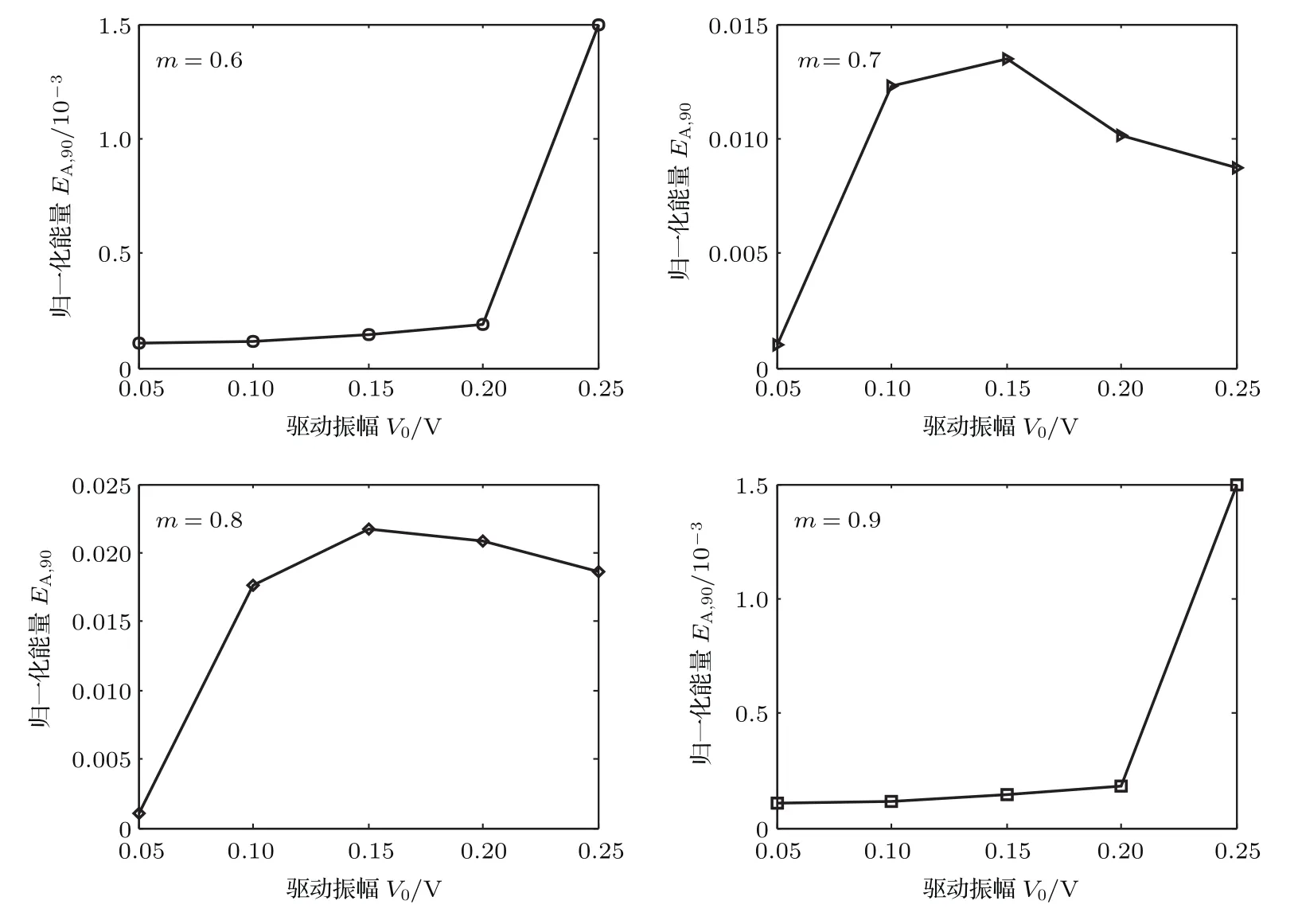
圖7 不同缺陷下EA,90和V0的關系(驅動頻率f=1.2 MHz)Fig.7.The EA,90 versus V0with different impurities for a driving frequency of 1.2 MHz.

3.3 電容電感缺陷

前面關注的都是電容缺陷,當m=0.6,V0=0.15 V,非線性LC電路系統不能產生孤子非對稱傳輸現象.在不改變缺陷系數和驅動振幅下,如何進一步實現孤子非對稱傳輸呢? 如圖8所示,在第一個單元結構中,繼續引入電感缺陷LI=nL,其中n同樣是缺陷系數.數值模擬中取n=3.3,其他器件及參數與上文一樣.圖9是電容電感缺陷下,時間t=3 ms、分別從A,B端驅動時電路系統內的波形.我們看到刻意的電感缺陷引入,促使原本不能產生孤子的非線性LC電路繼續發射孤子,而B端驅動能量依舊指數衰減,不能長距離傳輸,因此繼續實現了孤子非對稱傳輸.

圖8 電感電容缺陷Fig.8.Impurties of inductance and capacitance.

圖9 t=3 ms,m=0.6,n=3.3,分別從A,B端驅動時,電路系統內的波形(驅動參數如圖4)Fig.9.Waveforms of the electrical line which is drived from A and B respectively at t=3 ms,m=0.7 and n=3.2.The driving parameters are as same as in Fig.4.

4 結 論

本文采用數值模擬的方法對有缺陷的非線性LC電路中的孤子非對稱傳輸進行了研究.當驅動緊鄰缺陷時,驅動頻率接近缺陷本征頻率,驅動振幅小于非線性LC電路的電壓閾值,電路產生可傳播的孤子.而當驅動遠離缺陷時,電路中幾乎沒有能量流通,即出現孤子不對稱傳輸現象.這是因為缺陷靠近外界驅動時,驅動頻率接近缺陷處本征頻率,產生缺陷共振現象,即局域的振動模式將會進入非線性共振態,進而引起局域波動模式的不穩定,隨后釋放能量,產生可傳播的非線性波——包絡孤子,并不是非線性導致的倍頻波.而當缺陷遠離驅動時,能量在電路中劇烈衰減,缺陷幾乎吸收不到能量,達不到再次釋放能量的級別,因此電路不導通.進一步討論了非線性LC電路傳輸能量、缺陷系數和驅動振幅三者的關系.本文還關注了電容電感缺陷下的孤子非對稱傳輸,引入電感缺陷,為進一步調整非線性LC電路孤子不對稱傳輸提供了一種新的思維方法.同等條件下,選擇合適的缺陷,缺陷共振吸收驅動能量的能力遠大于沒有缺陷的電路,因此該電路可實現小驅動振幅下孤子的非對稱傳輸,且將驅動能量轉化成孤子能量的效率較高.

本文研究的是線性電容缺陷系數m＜1時的情況,但是這種方法同樣適用于電容缺陷系數m＞1及研究單獨的電感缺陷.鑒于電學、聲學、力學三者系統方程的一致性,可以把聲學系統、力學系統轉化為相應的電學線路來考慮問題,有助于方便地解決問題.另外,熱學的一些熱傳導問題可轉化為宏觀的晶格模型系統來模擬,因而該電路的設計和分析內容可以融合到聲、力、熱的領域,為解決相關問題提供一種思路.本文設計的缺陷電路和相關內容也為下一步的相關實驗提供了一定的理論基礎.

[1]Li X F,Ni X,Feng L,Lu M H,He C,Chen Yf2011 Phys.Rev.Lett.106 084301

[2]Liang B,Yuan B,Cheng J C 2009 Phys.Rev.Lett.103 104301

[3]Li B,Wang L,Casati G 2004 Phys.Rev.Lett.93 184301

[4]Hu B,Yang L,Zhang Y 2006 Phys.Rev.Lett.97 124302

[5]Konotop V V,Kuzmiak V 2002 Phys.Rev.B 66 235208

[6]Wang J W,Yuan B G,Cheng Y,Liu X J 2015 Sci.China:Phys.Mech.Astron.58 1

[7]Boechler N,Theocharis G,Daraio C 2011 Nature Mater.10 665

[8]Tao F,Chen W,Xu W,Pan J T,Du S D 2011 Phys.Rev.E 83 056605

[9]Tao F,Chen W Z,Xu W,Du S D 2012 Acta Phys.Sin.61 134103(in Chinese)[陶峰,陳偉中,許文,都思丹2012物理學報61 134103]

[10]Hirota R,Suzuki K 1970 J.Phys.Soc.Jpn.28 1366

[11]Motcheyo A B T,Tchawoua C,Siewe M S,Tchameu J D T 2013 Commu.Nonlinear Sci.Numer.Simulat.18 946

[12]Leon J 2003 Phys.Lett.A 319 130

[13]Marquie P,Bilbault J M,Remoissenet M 1994 Phys.Rev.E 49 828

[14]Kuusela T 1995 Chaos Solut Fract.5 2419

[15]Haus H A,Wong W S 1996 Rev.Mod.Phys.68 423

[16]Yu G K,Wang X L,Tao Z 2011 Phys.Rev.E 83 026605

[17]Liu C,Du Z,Sun Z,Gao H J,Guo X 2015 Phys.Rev.Appl.3 064014

[18]Remoissenet M 1999 Waves Called Solitons:Concepts and Experiments(2nd Ed.)(Berlin:Springer-Verlag)pp37–97

[19]Koon K T V,Leon J,Marquie P,Dinda P T 2007 Phys.Rev.E 75 066604

[20]Nagahama K,Yajima N 1989 J.Phys.Soc.Jpn.58 1539

[21]Pan J T,Chen W Z,Tao F,Xu W 2011 Phys.Rev.E 83 016601

PACS∶05.45.Yv,43.25.RqDOI∶10.7498/aps.66.100502

*Project supported by the National Natural Science Foundation of China(Grant Nos.11174140,11574149).

?Corresponding author.E-mail:shitoucheng_w@sina.com

Defect induced asymmetric soliton transmission in the nonlinear circuit?

Liu Hao-Hua Wang Shao-Hua?Li Bo-Bo Li Hua-Lin
(Institute of Acoustics,Key laboratory of Modern Acoustics of Ministry of Education,Nanjing University,Nanjing 210093,China)

8 November 2016;revised manuscript

2 March 2017)

Electrical diode,thefirst device to rectify the currentflux,has significantly revolutionized fundamental science and advanced technology in various aspects of our routine life.Motivated by the one-way rectification effect,considerable effort has been dedicated to the study of the unidirectional transmission in other physical systems for the potential applications,such as the acoustic diode,thermal diode,etc.The nonlinear LC circuit,which has unique advantages in the measurement of energy with which the voltage and current can be achieved by digitaloscilloscope conveniently,provides a simple and effective way of studying the nonlinear wave propagation in a dispersive medium.In this paper,we design a defective LC nonlinear circuit deliberately to realize asymmetric transmission of energy,and the energy carrier is nonlinear wave which is so-called soliton,instead of the linear wave in the pass band.The defect-induced localized wave is a kind of intrinsic bound-state wave mode that is evanescent away from the defect site but vibrates around the site with an intrinsic frequency fr.In the LC circuit,when the defect is close to the driver,with the frequency of driven signal in the forbidden band of system approaching to the intrinsic resonance frequency frof the defect,the resonance induced by the defect enables the circuit to turn on,which is relevant to but somewhat different from what was uncovered by Leon et al.about the intrinsic instability of evanescent waves stirred up directly by a boundary drive.On the other hand,the system acts like an insulator,for the defect is far away from the drive.The defect changes the homogeneity of the line,which allows the soliton to be released in one direction by the local resonance,with the driver being at a lower amplitude.As a result,the introducing of defects significantly improves conversion efficiency from the driver energy into the soliton.To further understand this phenomenon in the defective LC nonlinear circuit,we numerically investigate the relationship among transmission energy,defect coefficient and driver amplitude.Finally,the combined defects are also considered to further adjust the LC nonlinear circuit.

∶impurity,nonlinear circuit,soliton,energy

?國家自然科學基金(批準號:11174140,11574149)資助的課題.

?通信作者.E-mail:shitoucheng_w@sina.com

?2017中國物理學會Chinese Physical Society