計(jì)算相位響應(yīng)曲線的方波擾動(dòng)直接算法?
謝勇程建慧
(西安交通大學(xué)航天航空學(xué)院,機(jī)械結(jié)構(gòu)強(qiáng)度與振動(dòng)國(guó)家重點(diǎn)實(shí)驗(yàn)室,西安 710049)
計(jì)算相位響應(yīng)曲線的方波擾動(dòng)直接算法?
謝勇?程建慧
(西安交通大學(xué)航天航空學(xué)院,機(jī)械結(jié)構(gòu)強(qiáng)度與振動(dòng)國(guó)家重點(diǎn)實(shí)驗(yàn)室,西安 710049)
(2016年11月25日收到;2017年1月6日收到修改稿)
通過(guò)相位響應(yīng)曲線可對(duì)具有極限環(huán)周期運(yùn)動(dòng)的動(dòng)力系統(tǒng)的性質(zhì)有更為深入的理解.神經(jīng)元是一個(gè)典型的動(dòng)力系統(tǒng),因此相位響應(yīng)曲線提供了一種研究神經(jīng)元重復(fù)周期放電行為的新思路.本文提出一種求解相位響應(yīng)曲線的方法,即方波擾動(dòng)的直接算法,通過(guò)Hodgkin-Huxley,FitzHugh-Nagumo,Morris-Lecar和Hindmarsh-Rose神經(jīng)元模型驗(yàn)證該算法可計(jì)算周期峰放電、周期簇放電的相位響應(yīng)曲線.該算法克服了其他算法在運(yùn)用過(guò)程中的局限性.利用該算法計(jì)算結(jié)果表明:周期峰放電的相位響應(yīng)曲線類(lèi)型是由其分岔類(lèi)型所決定;在Morris-Lecar模型中發(fā)現(xiàn)一種開(kāi)始于Hopf分岔終止于鞍點(diǎn)同宿軌道分岔的閾上周期振蕩,其相位響應(yīng)曲線屬于第二類(lèi)型.通過(guò)大量的相位響應(yīng)曲線的計(jì)算發(fā)現(xiàn)相位響應(yīng)的相對(duì)大小及正負(fù)性僅取決于擾動(dòng)所施加的時(shí)間,而且周期簇放電的相位響應(yīng)曲線比周期峰放電的相位響應(yīng)曲線更為復(fù)雜.
相位響應(yīng)曲線,峰放電,簇放電,分岔
1 引 言
神經(jīng)元和神經(jīng)元所組成的神經(jīng)系統(tǒng)具有高度復(fù)雜的動(dòng)力學(xué)行為,呈現(xiàn)明顯的非線性現(xiàn)象,因此從非線性動(dòng)力學(xué)角度研究和理解神經(jīng)元和神經(jīng)系統(tǒng)的行為規(guī)律是十分必要的.其研究的一般思路是建立動(dòng)力學(xué)模型,然后利用動(dòng)力學(xué)系統(tǒng)理論解讀神經(jīng)元和神經(jīng)系統(tǒng)活動(dòng)規(guī)律及其動(dòng)力學(xué)機(jī)理.在神經(jīng)元建模方面,英國(guó)生理學(xué)家Hodgkin和Huxley[1]建立了Hodgkin-Huxley(HH)模型,它能很好地描述槍烏賊的神經(jīng)元峰放電(spiking)行為.這一開(kāi)創(chuàng)性工作成為定量研究可興奮生物細(xì)胞電生理特性的里程碑.為了便于理論分析,在1961年和1962年,FitzHugh和Nagumo等分別獨(dú)立地導(dǎo)出了一個(gè)由多項(xiàng)式表達(dá)的二維FitzHugh-Nagumo(FHN)模型[2,3].該模型盡管形式非常簡(jiǎn)潔,卻抓住了神經(jīng)元興奮的本質(zhì)特征.1981年,Morris和Lecar[4]結(jié)合HH模型和FHN模型各自的優(yōu)點(diǎn)提出了一個(gè)描述藤壺(一種甲殼綱的小動(dòng)物)肌肉纖維電生理特征的二維Morris-Lecar(ML)模型,現(xiàn)在也被作為神經(jīng)元模型而廣泛引用.隨后,Hindmarsh和Rose[5]為了解釋“尾電流反轉(zhuǎn)(tail current reversal)”現(xiàn)象提出了Hindmarsh-Rose(HR)模型.HR模型可以呈現(xiàn)峰放電和簇放電(bursting)行為.目前針對(duì)不同生物和不同類(lèi)型的神經(jīng)元已經(jīng)建立了大量的模型[6].有了神經(jīng)元模型,接下來(lái)就可以通過(guò)非線性動(dòng)力學(xué)理論分析神經(jīng)元復(fù)雜而豐富的放電行為,并揭示其發(fā)生的動(dòng)力學(xué)機(jī)理.已有大量的理論或數(shù)值分析確定神經(jīng)元模型中分岔、混沌和分形等非線性現(xiàn)象[7?17].噪聲無(wú)處不在,對(duì)隨機(jī)共振現(xiàn)象的研究表明噪聲可能增強(qiáng)神經(jīng)元、神經(jīng)元網(wǎng)絡(luò)以及神經(jīng)系統(tǒng)檢測(cè)微弱信號(hào)的能力[18?22].
通過(guò)對(duì)神經(jīng)元模型的數(shù)值計(jì)算很容易再現(xiàn)神經(jīng)元各種復(fù)雜的放電模式,比如周期峰放電、周期簇放電、混沌峰放電、混沌簇放電和整數(shù)倍放電等.本文主要關(guān)注周期峰放電和周期簇放電兩種放電模式.這兩種放電模式從非線性動(dòng)力學(xué)角度講都是極限環(huán)振子,而描述極限環(huán)的最簡(jiǎn)單的方式就是采用振子的相位.通過(guò)相位變換就可以把復(fù)雜的狀態(tài)空間模型映射到一維的相位模型,這樣有助于獲得振子系統(tǒng)的解析解.處于極限環(huán)運(yùn)動(dòng)狀態(tài)的振子系統(tǒng)對(duì)外界刺激的響應(yīng)特征可以通過(guò)相位響應(yīng)曲線(phase response curve,PRC)進(jìn)行刻畫(huà)[23,24],相位響應(yīng)曲線有時(shí)也稱為相位重置曲線(phase resetting curve,PRC).PRC是一個(gè)關(guān)于相位的函數(shù),它是指極限環(huán)振子在不同相位處由外界擾動(dòng)引起振蕩周期的暫態(tài)變化.
PRC是由文獻(xiàn)[25,26]在研究生物節(jié)律的重置過(guò)程中引入的,在很多方面都有極其重要的作用,隨后被應(yīng)用到神經(jīng)元系統(tǒng)中.在相空間中PRC表示擾動(dòng)后周期振子相位的提前或滯后.如果周期振子的周期縮短了,則稱為相位提前(phase advance);相反,如果周期變長(zhǎng)了,則稱為相位滯后(phase delay).在研究生物節(jié)律時(shí),PRC已成為研究的標(biāo)準(zhǔn)工具.比如人體對(duì)光刺激的PRC是調(diào)整睡眠時(shí)間療法的理論基礎(chǔ).在心臟病學(xué)中,PRC可用來(lái)理解各種心律失常的發(fā)生[27,28].在神經(jīng)科學(xué)中,相位簡(jiǎn)化模型可用來(lái)簡(jiǎn)化復(fù)雜的神經(jīng)科學(xué)的生物模型[29?31].如果知道一個(gè)振子系統(tǒng)的PRC,就可以很容易地預(yù)測(cè)該振子在受到外界刺激時(shí)的行為.另外,PRC可用來(lái)預(yù)測(cè)周期刺激的拖帶(entrainment)以及耦合振子的相鎖(phase locking),還可以用來(lái)理解相干振蕩器、行波(traveling waves)等動(dòng)力學(xué)行為.耦合神經(jīng)元的相互作用函數(shù)可以通過(guò)PRC數(shù)值計(jì)算得到[32].文獻(xiàn)[33]詳細(xì)介紹了神經(jīng)科學(xué)中PRC及其應(yīng)用.已有的研究表明周期峰放電的神經(jīng)元的PRC可分為兩大類(lèi)[23]:第一類(lèi)型PRC是指PRC取值全為正或者全為負(fù),這樣興奮性擾動(dòng)將導(dǎo)致峰放電提前或者滯后;而第二類(lèi)型PRC是指PRC取值是兩相的,部分為正,部分為負(fù),這樣將導(dǎo)致當(dāng)擾動(dòng)施加在不同的相位處時(shí),部分相位處將引起放電提前,而部分相位處引起放電滯后.
而PRC的類(lèi)型與神經(jīng)元從靜息到周期峰放電所跨越的分岔類(lèi)型密切相關(guān).具體地講,具有第一類(lèi)型PRC的神經(jīng)元跨越了不變圓上的鞍結(jié)分岔(saddle-node on invariant circle bifurcation,SNIC),而具有第二類(lèi)型PRC的神經(jīng)元?jiǎng)t經(jīng)歷了Hopf分岔.因此PRC的類(lèi)型與神經(jīng)元的興奮性類(lèi)型一一對(duì)應(yīng).
周期簇放電的PRC與周期峰放電的PRC定義類(lèi)似,是指簇放電神經(jīng)元在受到外界擾動(dòng)時(shí)下一個(gè)簇到來(lái)時(shí)刻與未擾動(dòng)的簇之間的相位差.對(duì)于周期簇放電的PRC與其分岔類(lèi)型之間的關(guān)系,現(xiàn)在的研究還比較少,它們之間的關(guān)系還不清楚.不過(guò),要弄清這一關(guān)系的前提就是首先要計(jì)算獲得周期簇放電的PRC.
PRC可通過(guò)實(shí)驗(yàn)或理論分析得到.在進(jìn)行理論分析時(shí),需要知道動(dòng)力系統(tǒng)具體的表達(dá)式.對(duì)于一些簡(jiǎn)單的模型,其PRC可通過(guò)相位簡(jiǎn)化方法得到其解析解;但對(duì)復(fù)雜的、非線性的神經(jīng)元模型,往往無(wú)法解析求解,因此有必要通過(guò)數(shù)值計(jì)算得到其PRC.目前計(jì)算PRC的基本思路有兩種[32]:一種是根據(jù)PRC的定義,即用神經(jīng)元振子對(duì)短的脈沖刺激的響應(yīng)直接計(jì)算,該思路比較簡(jiǎn)單,但擾動(dòng)是有限幅值擾動(dòng),導(dǎo)致計(jì)算結(jié)果不是很精確;另一種是將神經(jīng)元振子在極限環(huán)附近線性化,求解線性伴隨方程,然而求解伴隨方程需要向后積分且不穩(wěn)定,因此該算法并不簡(jiǎn)單.不過(guò)該算法是一些軟件求解PRC的依據(jù),比如XPPAUT[34]和MatCont[35].對(duì)于前一種思路所對(duì)應(yīng)的直接算法中,通常在膜電位上施加典型的峰擾動(dòng),這一典型峰是取自簇放電本身的一個(gè)尖峰,該擾動(dòng)形式更接近實(shí)際的生理過(guò)程.但該方法是針對(duì)簇放電的,而且典型的峰擾動(dòng)所需確定的參數(shù)較多,比如對(duì)于HR模型,需要確定5個(gè)參數(shù),方程增加一維,計(jì)算費(fèi)時(shí)[36].無(wú)限小擾動(dòng)的改進(jìn)算法也是直接算法的一種[37],該算法計(jì)算速度快.但該算法本質(zhì)在于求解特征矩陣,在計(jì)算簇放電神經(jīng)元模型的PRC時(shí),容易溢出,出現(xiàn)錯(cuò)誤.例如該算法應(yīng)用于Chay模型和Wang模型時(shí),就出現(xiàn)了溢出錯(cuò)誤.因此基于上述算法的局限性,本文提出了一種基于PRC定義的直接算法,以方波擾動(dòng)作為擾動(dòng)形式,該算法可適用于峰放電和簇放電.
本文內(nèi)容安排如下:第2部分首先介紹我們的直接算法,通過(guò)HH模型驗(yàn)證該算法的可行性,然后將該算法運(yùn)用到FHN模型中,揭示FHN神經(jīng)元的PRC類(lèi)型;第3部分利用本文的直接算法通過(guò)ML模型探究周期峰放電模型的PRC的表現(xiàn)特征,揭示分岔機(jī)理與PRC類(lèi)型之間的關(guān)系;第4部分通過(guò)HR模型驗(yàn)證該算法同樣適用于計(jì)算周期簇放電的PRC;第5部分是結(jié)論.
2 PRC的直接算法及算例
2.1 方波擾動(dòng)的直接算法
對(duì)一個(gè)自治動(dòng)力系統(tǒng),其模型可定義為

其中,X=(x1,x2,...,xN)為N 維相空間的狀態(tài)變量.記該系統(tǒng)的解為X(t)=Ψ(X0,t),其中X0=X(0)是初始值.假定該系統(tǒng)存在一個(gè)穩(wěn)定的極限環(huán),其周期為T(mén).在極限環(huán)上選取一點(diǎn)作為初始點(diǎn),即,則可得到一個(gè)沿著極限環(huán)移動(dòng)的周期為T(mén)的跡線,即.而位于極限環(huán)上的一點(diǎn)的相位可以由兩種不同的方式進(jìn)行定義:一種是空間相位,按照極限環(huán)的長(zhǎng)度均勻增加進(jìn)行度量;另一種以一狀態(tài)變量沿著極限環(huán)時(shí)間均勻增加進(jìn)行度量.根據(jù)相位簡(jiǎn)化方法,本文采用后一種定義,因?yàn)樵摱x可得到一個(gè)簡(jiǎn)單的相位公式.如果認(rèn)為極限環(huán)上的初始點(diǎn)相位為0,則極限環(huán)上其他點(diǎn)的相位為

對(duì)系統(tǒng)在極限環(huán)上一點(diǎn)x0處施加一擾動(dòng)?F,若該擾動(dòng)僅使得該點(diǎn)沿極限環(huán)偏移,則該擾動(dòng)的作用僅是增加或減少動(dòng)力系統(tǒng)的周期,或者說(shuō)延遲或提前擾動(dòng)后的跡線回到點(diǎn)x0處的時(shí)間,則該點(diǎn)的相位響應(yīng)為

其中t0為未加擾動(dòng)從點(diǎn)x0處出發(fā)第一次回到點(diǎn)x0處的時(shí)間,0為擾動(dòng)后第一次回到x0處的時(shí)間,為擾動(dòng)后的周期.PR表示相位響應(yīng)(phase response).
小幅值的擾動(dòng)?F通常用來(lái)模擬一個(gè)瞬時(shí)的增加或減小后突觸神經(jīng)元的電流作用,而忽略關(guān)于離子通道參數(shù)的影響.在計(jì)算此類(lèi)擾動(dòng)的PRC時(shí),先數(shù)值積分未擾動(dòng)的系統(tǒng)F到施加擾動(dòng)相位(或時(shí)刻),再積分?jǐn)_動(dòng)后的系統(tǒng),積分區(qū)間長(zhǎng)度為擾動(dòng)持續(xù)的時(shí)間長(zhǎng)度,然后繼續(xù)數(shù)值積分原系統(tǒng)F,最后相位響應(yīng)根據(jù)(3)式求解,則PRC由施加在[0,1)區(qū)間上的擾動(dòng)所對(duì)應(yīng)的相位響應(yīng)構(gòu)成.這就是本文計(jì)算PRC的直接算法.在計(jì)算PRC過(guò)程時(shí),常常假定擾動(dòng)后的跡線會(huì)在一次放電環(huán)后回到極限環(huán)周期軌道上,并以下一次放電環(huán)上的參考相位(周期峰放電一般選取膜電位最高的尖峰時(shí)刻)來(lái)測(cè)量相位響應(yīng).此外還需要注意的是,選取未擾動(dòng)的極限環(huán)軌道上的一點(diǎn)作為參考點(diǎn)表明開(kāi)始時(shí)間,記為t=0,相位θ=0.本文中的擾動(dòng)為方波擾動(dòng),其擾動(dòng)幅值為Ip,持續(xù)時(shí)間為tp,即在擾動(dòng)持續(xù)時(shí)間tp內(nèi)擾動(dòng)幅值保持常數(shù)Ip,因此稱為方波擾動(dòng).該擾動(dòng)施加在表示神經(jīng)元膜電位變化的微分方程右端項(xiàng)上,對(duì)有生理意義的神經(jīng)元模型而言,可以表示為,其中C為膜電容.記膜電位在受到外界擾動(dòng)時(shí)的PRC為PRC1,由于本文后面的計(jì)算都是在膜電位上施加外界擾動(dòng),因此我們用PRC來(lái)表示PRC1,不再進(jìn)行區(qū)分.關(guān)于方波擾動(dòng)的參數(shù)Ip,tp的選擇,對(duì)周期峰放電而言,Ip的大小取決于膜電位的變化幅值以及模型中外加電流的大小(若存在),可取膜電位幅值或者外加電流大小的1/20—1/5;tp的值取決于周期的大小,并且盡量持續(xù)時(shí)間較短,一般情況下選取不超過(guò)峰放電的脈沖寬度.對(duì)周期簇放電而言,tp的值一般不超過(guò)簇內(nèi)一個(gè)尖峰動(dòng)作電位的持續(xù)時(shí)間;Ip的取值類(lèi)似周期峰放電,但對(duì)于周期簇放電,要注意在擾動(dòng)作用下簇內(nèi)的尖峰個(gè)數(shù)不能發(fā)生變化.具體的算法實(shí)現(xiàn)過(guò)程為:
1)計(jì)算神經(jīng)元周期峰放電或周期簇放電所對(duì)應(yīng)的極限環(huán)及其周期,記周期為T(mén)0,對(duì)神經(jīng)元系統(tǒng)進(jìn)行時(shí)間尺度變換,將周期變換為1,可參考文獻(xiàn)[37];
2)在極限環(huán)上選取參考相位,記為t0(對(duì)周期峰放電,一般選取膜電位最大的時(shí)刻作為參考相位;對(duì)周期簇放電,一般選擇第一個(gè)尖峰膜電位最大的時(shí)刻作為參考相位);
3)將極限環(huán)按時(shí)間等間距分為n個(gè)區(qū)間,n=1/tp,在不存在擾動(dòng)時(shí),按未擾動(dòng)系統(tǒng)數(shù)值積分,在存在擾動(dòng)的[(m?1)tp,mtp]時(shí)間范圍內(nèi),按擾動(dòng)系統(tǒng)數(shù)值積分,其中1≤m≤n;記錄第一次回到參考相位的時(shí)間,記為0;根據(jù)(3)式計(jì)算每個(gè)節(jié)點(diǎn)處的PRC值,若大于0則為相位提前,若小于0表示相位滯后.
2.2 HH神經(jīng)元模型周期峰放電的PRC
為了與現(xiàn)有的文獻(xiàn)計(jì)算結(jié)果比較來(lái)說(shuō)明本文提出的直接算法的正確性,特意選擇文獻(xiàn)[37]中的HH神經(jīng)元模型算例.HH神經(jīng)元模型的具體形式如下:

其中V為膜電位;C為膜電容;m,h為Na離子通道的門(mén)控變量;n為K離子通道的門(mén)控變量;gK,gNa和gL分別為K離子通道、Na離子通道和漏電流的最大電導(dǎo);VK,VNa和VL分別為它們各自的反轉(zhuǎn)電位;Iapp為外加電流強(qiáng)度.an(V),bn(V),am(V),bm(V),ah(V)和bh(V)滿足:
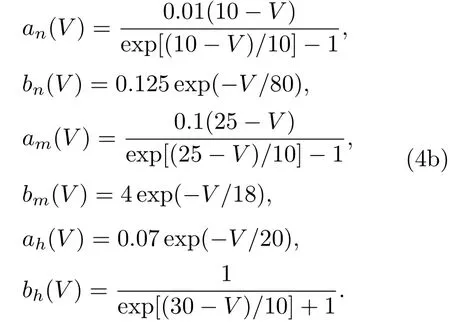
選取參數(shù)

其中電導(dǎo)單位為mS/cm2,電壓?jiǎn)挝粸閙V,電容單位為μF/cm2,電流單位為μA/cm2.
在上述參數(shù)取值條件下HH模型存在兩個(gè)穩(wěn)定的極限環(huán),分別稱為外極限環(huán)和內(nèi)極限環(huán).本文所取初始條件分別為(5.25,0.07,0.60,0.011)和(7.25,0.17,0.13,0.55),如圖1所示.
通過(guò)分岔軟件XPPAUT對(duì)HH模型做膜電位關(guān)于外加電流強(qiáng)度的分岔分析,發(fā)現(xiàn)有兩個(gè)區(qū)間存在兩個(gè)穩(wěn)定極限環(huán)共存的情形,它們分別是[34.95,38.51]和[40.01,41.28],如圖2所示.圖2(b)是圖2(a)的局部放大.圖中粗實(shí)線表示穩(wěn)定平衡態(tài),點(diǎn)劃線表示不穩(wěn)定平衡態(tài),細(xì)實(shí)線表示穩(wěn)定極限環(huán)的振蕩最大和最小值,而點(diǎn)線表示不穩(wěn)定極限環(huán)的振蕩最大和最小值(本文中所有分岔圖都采用這種表達(dá)方式).HB表示Hopf分岔;FLC表示極限環(huán)折疊分岔(fold limit cycle bifurcation),有時(shí)也叫極限環(huán)鞍結(jié)分岔(saddle-node bifurcation of limit cycles).可以看出圖1中兩個(gè)共存的極限環(huán)正是在第二狹窄區(qū)間里取Iapp=41獲得的.

圖1 HH神經(jīng)元模型兩個(gè)共存的穩(wěn)定極限環(huán)在(V,m)相平面上的投影Fig.1.The(V,m)projections of two coexisting stable limit cycles of the HH neuron model.
接下來(lái)運(yùn)用本文的直接算法計(jì)算HH模型內(nèi)、外極限環(huán)的PRC.對(duì)內(nèi)極限環(huán)所施加的擾動(dòng)為Ip=10,tp=0.004,計(jì)算步長(zhǎng)為0.001(周期歸一化為1,以下同此做法);對(duì)外極限環(huán)所施加的擾動(dòng)為Ip=5,tp=0.004,計(jì)算步長(zhǎng)為0.0001.這樣HH神經(jīng)元模型的內(nèi)、外極限環(huán)的PRC如圖3所示.我們的計(jì)算結(jié)果與文獻(xiàn)[30]的結(jié)果除了幅值不同以外幾乎完全一致,事實(shí)上,PRC相對(duì)值才具有意義.值得注意的是,由于在極限環(huán)上所取的初始參考點(diǎn)不一樣造成PRC開(kāi)始的位置不同,但波動(dòng)順序是完全一致的,從而說(shuō)明本文的算法是可信的.
由圖3可知,無(wú)論內(nèi)極限環(huán)還是外極限環(huán),HH神經(jīng)元模型的PRC值既有正值又有負(fù)值,這表明HH神經(jīng)元模型的PRC為第二類(lèi)型PRC.由前面的分岔分析可知HH神經(jīng)元模型從靜息到放電的確經(jīng)歷了一個(gè)次臨界Hopf分岔.

圖2 HH神經(jīng)元模型膜電位對(duì)外加電流強(qiáng)度的分岔圖Fig.2.Bifurcation diagram of the membrane potential V versus the strength of the applied current Iappin the HH neuron model.

圖3 (a)內(nèi)極限環(huán)的PRC;(b)外極限環(huán)的PRCFig.3.(a)The PRC of the inner limit cycle;(b)the PRC of the outer limit cycle.
2.3 FHN神經(jīng)元模型周期峰放電的PRC
FHN神經(jīng)元模型的放電行為和分岔機(jī)理都有相關(guān)的研究,但是對(duì)其PRC的計(jì)算還較為少見(jiàn),因此本文采用方波擾動(dòng)的直接算法計(jì)算其PRC.FHN神經(jīng)元模型的形式如下[2,3]:

其中V表示膜電位;w表示恢復(fù)變量;a,b,c為系統(tǒng)參數(shù);Iapp為外加電流強(qiáng)度.FHN模型是一個(gè)無(wú)量綱的神經(jīng)元模型.
取參數(shù)a=0.139,b=2.54,c=0.008,分析FHN神經(jīng)元模型隨外加電流強(qiáng)度的分岔機(jī)理,如圖4所示.
由圖4可知,當(dāng)I=0.03469時(shí),神經(jīng)元經(jīng)歷一個(gè)次臨界Hopf分岔由靜息態(tài)變?yōu)橹芷诜宸烹?當(dāng)I=0.1509時(shí),經(jīng)歷另外一個(gè)次臨界Hopf點(diǎn),由周期峰放電變?yōu)殪o息態(tài).運(yùn)用直接算法計(jì)算該模型的PRC,所施加擾動(dòng)Ip=0.002,tp=0.004,計(jì)算步長(zhǎng)為0.001,其放電模式與PRC的對(duì)應(yīng)關(guān)系如圖5所示.

圖4 FHN神經(jīng)元模型的分岔圖Fig.4.Bifurcation diagram of the membrane potential versus the applied current strength in the FHN neuron model.
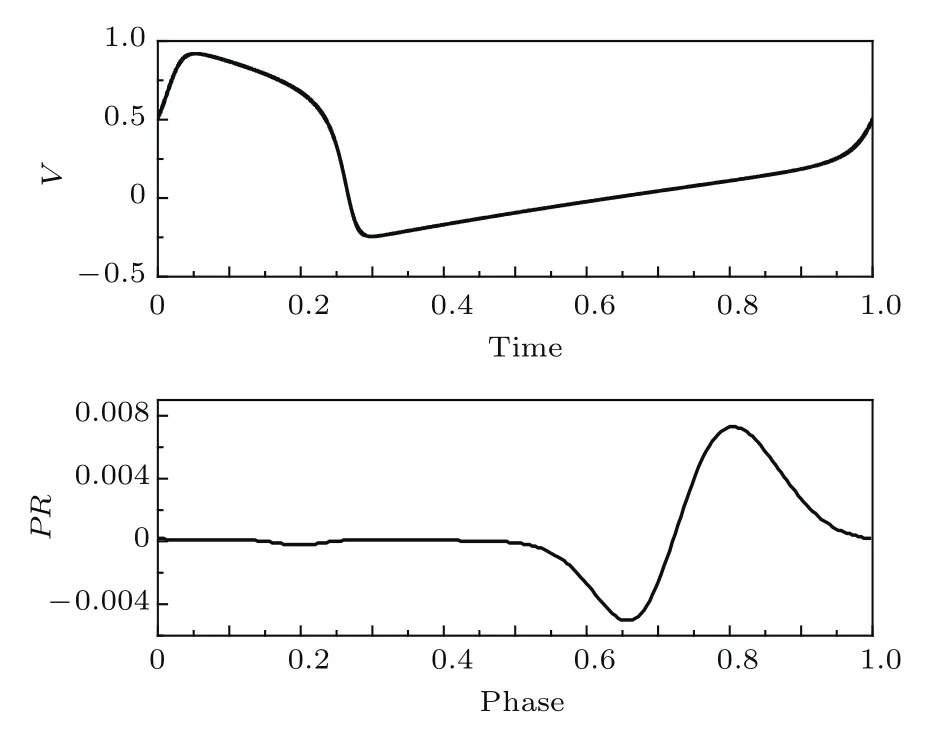
圖5 FHN神經(jīng)元模型的放電形式及其對(duì)應(yīng)的PRCFig.5.Periodic spiking and its corresponding PRC in the FHN neuron model.
從圖5可以看到FHN神經(jīng)元模型的PRC取值有正有負(fù),表現(xiàn)為第二類(lèi)型的PRC.這與神經(jīng)元所經(jīng)歷的Hopf分岔密切相關(guān).而且PRC的幅值最大值并不與神經(jīng)元放電的尖峰時(shí)刻存在對(duì)應(yīng)關(guān)系,而是取值取決于擾動(dòng)所施加的時(shí)間.同時(shí)還可以看到PRC在前半周期取值幾乎接近于0,在后半周期才出現(xiàn)明顯的變化.這是由于在放電尖峰附近對(duì)外部擾動(dòng)不敏感,而隨之出現(xiàn)的超極化區(qū)域所占時(shí)間又較長(zhǎng),因此導(dǎo)致了較長(zhǎng)區(qū)域的PRC取值幾乎為0.
3 ML模型的PRC
由于ML模型在不同參數(shù)條件下隨外加電流強(qiáng)度有著不同的分岔行為,因此計(jì)算ML模型的PRC能更充分地揭示分岔與PRC形狀的關(guān)系.ML模型有三種電流,即鉀電流、鈣電流和漏電流,具體形式為[4]
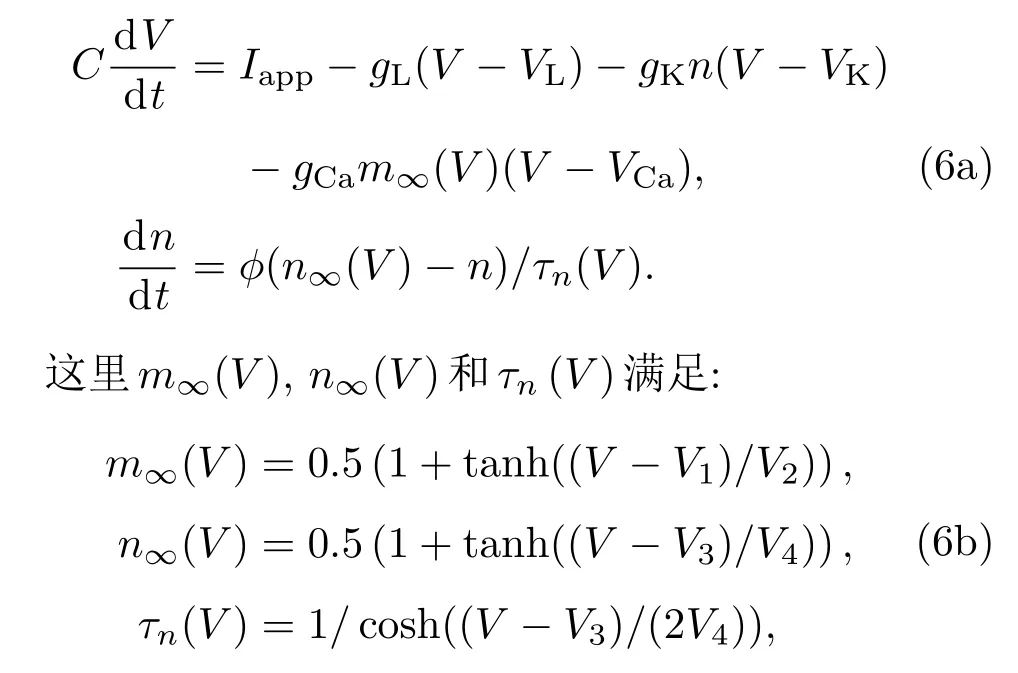
其中V表示膜電位變量;n為恢復(fù)變量;C為膜電容;V1,V2,V3和V4為擬合電壓膜片鉗數(shù)據(jù)的參數(shù);?為快慢時(shí)間尺度比率;gCa,gK和gL分別為Ca離子通道、K離子通道和漏電流的最大電導(dǎo);VCa,VK和VL分別為它們各自的反轉(zhuǎn)電位;Iapp為外加電流強(qiáng)度.其中電導(dǎo)率單位為mS/cm2,電壓?jiǎn)挝粸閙V,電容單位為μF/cm2,電流單位為μA/cm2.
盡管ML模型是一個(gè)簡(jiǎn)單的、只含有兩個(gè)變量的動(dòng)力系統(tǒng),然而在不同的參數(shù)集下卻可以表現(xiàn)出豐富的放電行為[35,38].本文選取如下三組參數(shù)研究ML模型的動(dòng)力學(xué)特性,如表1所列.

表1 ML模型的參數(shù)集Table 1.Parameter sets of the ML model.
在上述三組參數(shù)條件下計(jì)算了ML模型隨外加電流強(qiáng)度變化的分岔行為.在第一組參數(shù)條件下,ML模型從靜息態(tài)到周期峰放電在Iapp=38.76處經(jīng)歷了一個(gè)SNIC,呈現(xiàn)第一類(lèi)型興奮性,如圖6(a)所示.圖6(b)是在第二組參數(shù)條件下,ML從靜息態(tài)到周期峰放電在Iapp=45.47處經(jīng)歷了一個(gè)次臨界Hopf分岔,呈現(xiàn)第二類(lèi)型興奮性.特別地,在第三組參數(shù)條件下,隨著外加電流強(qiáng)度逐漸增大,ML模型在Iapp=39.96處?kù)o息態(tài)通過(guò)一個(gè)平衡點(diǎn)的鞍結(jié)分岔消失,跳到一個(gè)由次臨界Hopf分岔而來(lái)的極限環(huán)上,呈現(xiàn)一個(gè)閾上的周期振蕩.這個(gè)極限環(huán)隨著外加電流強(qiáng)度逐漸減小,在Iapp=35.01處終止一個(gè)鞍點(diǎn)同宿軌道分岔(saddle homoclinic orbit bifurcation),如圖6(c)所示.從圖6(c)還可以看到存在一個(gè)由兩條豎直的短劃線所夾的狹窄區(qū)間,在此區(qū)間內(nèi),ML模型有兩個(gè)穩(wěn)定的平衡態(tài)和一個(gè)穩(wěn)定的極限環(huán),呈現(xiàn)三穩(wěn)態(tài).左邊的短劃線位于次臨界Hopf分岔處,而右邊的短劃線位于平衡點(diǎn)鞍結(jié)分岔處.
針對(duì)這三組參數(shù),取外加電流強(qiáng)度Iapp分別為39,45和39,可以發(fā)現(xiàn)前面兩種情形ML模型呈現(xiàn)周期峰放電,如圖7(a)和圖7(b)所示;而最后一種情形則表現(xiàn)為閾上周期振蕩,如圖7(c)所示.

圖6 ML模型在不同參數(shù)條件的分岔圖 (a)第一組參數(shù);(b)第二組參數(shù);(c)第三組參數(shù)Fig.6.Bifurcation diagrams of the membrane potential versus the applied current strength in the ML neuron model with di ff erent parameter sets:(a)The fi rst parameter set;(b)the second parameter set;(c)the third parameter set.

圖7 ML模型在不同參數(shù)條件的放電模式 (a)在第一組參數(shù)下當(dāng)Iapp=39時(shí)ML模型的周期峰放電;(b)在第二組參數(shù)條件下,當(dāng)Iapp=45時(shí)ML模型的周期峰放電;(c)在第三組參數(shù)條件下,當(dāng)Iapp=39時(shí)ML模型的閾上周期振蕩Fig.7.Firing patterns of the ML neuron model with di ff erent parameter sets:(a)Periodic spiking with the fi rst parameter set when Iapp=39;(b)periodic spiking with the second parameter set when Iapp=45;(c)suprathreshold periodic oscillation with the third parameter set when Iapp=39.
運(yùn)用直接算法計(jì)算ML模型在前面三組參數(shù)條件下當(dāng)Iapp分別等于39,45和39時(shí)的PRC.在第一組參數(shù)條件下,當(dāng)Iapp=39時(shí)所施加擾動(dòng)為Ip=20,tp=0.004,計(jì)算步長(zhǎng)為0.001,PRC如圖8(a)所示.在第二組參數(shù)條件下,當(dāng)Iapp=45時(shí)所施加擾動(dòng)為Ip=30,tp=0.004,計(jì)算步長(zhǎng)為0.001,PRC如圖8(b)所示.圖8(c)所示的PRC為在第三組參數(shù)條件下當(dāng)Iapp=39時(shí)的結(jié)果,此時(shí)所施加擾動(dòng)為Ip=?10,tp=0.005,計(jì)算步長(zhǎng)為0.001.

圖8 (a)在第一組參數(shù)下當(dāng)Iapp=39時(shí)ML模型的周期峰放電及其對(duì)應(yīng)的PRC;(b)在第二組參數(shù)條件下當(dāng)Iapp=45時(shí)ML模型的周期峰放電及其對(duì)應(yīng)的PRC;(c)在第三組參數(shù)條件下當(dāng)Iapp=39時(shí)ML模型的閾上周期振蕩及其對(duì)應(yīng)的PRCFig.8.Periodic oscillations and their corresponding PRCs in the ML neuron model with di ff erent parameter sets:(a)Periodic spiking and its corresponding PRC with the fi rst parameter set when Iapp=39;(b)periodic spiking and its corresponding PRC with the second parameter set when Iapp=45;(c)suprathreshold periodic oscillation and its corresponding PRC with the third parameter set when Iapp=39.
由ML模型的PRC計(jì)算結(jié)果可知,如果從靜息態(tài)到周期峰放電經(jīng)歷SNLC分岔,則屬于第一類(lèi)型興奮性,其PRC的類(lèi)型確為第一類(lèi)型,PRC取值幾乎全部為正.當(dāng)從靜息態(tài)到周期峰放電經(jīng)歷Hopf分岔時(shí),其興奮性屬于第二類(lèi)型,而其PRC取值既有正又有負(fù).在第三組參數(shù)條件下,當(dāng)Iapp=39時(shí)ML模型的PRC既有正值又有負(fù)值,表現(xiàn)為第二類(lèi)型的PRC.實(shí)際上,在第三組參數(shù)條件下,隨著外加電流強(qiáng)度減小,ML模型經(jīng)歷一個(gè)次臨界Hopf分岔產(chǎn)生閾上周期振蕩,該周期振蕩的極限環(huán)終止于一個(gè)鞍點(diǎn)同宿軌道分岔.對(duì)此情形尚無(wú)相關(guān)的文獻(xiàn)給出周期振蕩所對(duì)應(yīng)的PRC類(lèi)型.但由其分岔機(jī)理可知,周期振蕩是由Hopf分岔引起的,因此其PRC表現(xiàn)為第二類(lèi)型也是合乎情理的.同F(xiàn)HN神經(jīng)元模型的PRC計(jì)算結(jié)果一樣,ML模型的膜電位變化的尖峰時(shí)刻與其PRC取值的局部極值并不對(duì)應(yīng),這表明PRC僅取決于施加擾動(dòng)的時(shí)間.對(duì)ML模型而言,其在不同參數(shù)條件下表現(xiàn)出不同的分岔行為,因此決定其PRC可以表現(xiàn)為第一類(lèi)型或第二類(lèi)型,從而可通過(guò)調(diào)節(jié)參數(shù)來(lái)實(shí)現(xiàn)PRC類(lèi)型的改變.
4 方波擾動(dòng)直接算法計(jì)算周期簇放電PRC
為了驗(yàn)證本文直接算法對(duì)周期簇放電PRC計(jì)算的有效性,我們選擇HR神經(jīng)元模型進(jìn)行PRC計(jì)算,其主要原因是目前已有的文獻(xiàn)中只有HR模型的PRC結(jié)果可資以參考.HR神經(jīng)元模型形式如下[5]:

HR模型同F(xiàn)HN模型一樣,是無(wú)量綱的.式中x表示神經(jīng)元膜電位;y是峰變量,代表Na和K等快速離子通道電流;而z是簇變量,代表其他慢離子通道電流;a,b,c,d,s和x0為系統(tǒng)參數(shù);r為快慢時(shí)間尺度因子;Iapp為外加電流強(qiáng)度.本文選取a=1.0,b=3.0,c=1.0,d=5.0,s=4.0,x=?1.6,r=0.001.
與前面周期峰放電情形不同的是,在計(jì)算周期簇放電PRC時(shí),要注意所施加方波擾動(dòng)的強(qiáng)度和持續(xù)的時(shí)間.本文中僅考慮弱擾動(dòng),其具體表現(xiàn)為不改變簇放電簇內(nèi)的尖峰個(gè)數(shù).如果尖峰個(gè)數(shù)在擾動(dòng)下發(fā)生變化,則稱該擾動(dòng)為強(qiáng)擾動(dòng),如圖9所示,實(shí)線是未擾動(dòng)時(shí)簇放電模式,虛線是施加擾動(dòng)后的簇放電模式,顯然簇內(nèi)尖峰個(gè)數(shù)發(fā)生了變化.當(dāng)然在實(shí)際中強(qiáng)擾動(dòng)亦有其意義,但本文中不討論這一情形.值得注意的是,在算法實(shí)現(xiàn)過(guò)程中,參考相位一般選取第一個(gè)尖峰所對(duì)應(yīng)的時(shí)刻.
當(dāng)Iapp=1.3時(shí),HR神經(jīng)元模型簇內(nèi)尖峰個(gè)數(shù)為5,其放電模式和對(duì)應(yīng)的極限環(huán)如圖10所示.
運(yùn)用本文直接算法計(jì)算在該條件下HR神經(jīng)元模型周期簇放電的PRC.其中Ip=0.05,tp=10,步長(zhǎng)為0.0001,結(jié)果如圖11所示.

圖9 強(qiáng)擾動(dòng)下周期簇放電簇內(nèi)尖峰個(gè)數(shù)變化Fig.9.The variation of the number of spiking in a bursting under a strong perturbation.

圖10 HR神經(jīng)元模型的周期簇放電模式及其對(duì)應(yīng)的極限環(huán)Fig.10.Periodic bursting and its corresponding limit cycle in the HR neuron model.
運(yùn)用無(wú)限小擾動(dòng)的改進(jìn)算法的計(jì)算結(jié)果如圖12所示.
對(duì)比方波直接算法的結(jié)果與無(wú)限小擾動(dòng)的改進(jìn)算法的結(jié)果可知,二者僅存在PRC幅值大小的不同,而形狀、波動(dòng)趨勢(shì)和正負(fù)性幾乎完全相同.這表明本文方波擾動(dòng)直接算法亦可適用于計(jì)算周期簇放電的PRC.同時(shí)通過(guò)HR神經(jīng)元模型可以發(fā)現(xiàn)周期簇放電的PRC比周期峰放電的PRC有更為復(fù)雜的表現(xiàn)形式,最為明顯的一點(diǎn)是周期簇放電的PRC存在一個(gè)劇烈變化的區(qū)域,正好對(duì)應(yīng)于簇內(nèi)放電部分.

圖11 方波擾動(dòng)直接算法計(jì)算HR神經(jīng)元模型周期簇放電的PRCFig.11.PRC of periodic bursting in the HR neuron model using the direct method with square wave perturbation.

圖12 利用無(wú)限小擾動(dòng)的改進(jìn)算法時(shí)HR模型的PRCFig.12.PRC of periodic bursting in the HR neuron model using the modi fi ed direct method with in fi nitesimal perturbation.
5 結(jié) 論
本文提出了一個(gè)基于PRC的定義的方波擾動(dòng)直接算法,通過(guò)HH神經(jīng)元模型驗(yàn)證了該算法在計(jì)算周期峰放電的PRC是有效的.將該算法運(yùn)用于FHN神經(jīng)元模型,揭示了其PRC屬于第二類(lèi)型,這與FHN神經(jīng)元模型隨外加電流強(qiáng)度變化從靜息態(tài)到周期峰放電所跨越的Hopf分岔動(dòng)力學(xué)機(jī)理完全符合.然后考察了在三組不同的參數(shù)集條件下ML模型隨外加電流強(qiáng)度變化的分岔行為,并計(jì)算了在各自周期峰放電或閾上周期振蕩情形的PRC,表明通過(guò)調(diào)節(jié)相應(yīng)的參數(shù)可改變神經(jīng)元興奮性類(lèi)型,從而改變其PRC的類(lèi)型,揭示了分岔機(jī)理與PRC類(lèi)型之間的對(duì)應(yīng)關(guān)系.最后通過(guò)HR神經(jīng)元模型驗(yàn)證了本文算法對(duì)于計(jì)算周期簇放電的PRC也是可行的.通過(guò)大量的計(jì)算表明該算法對(duì)不同類(lèi)型的簇放電具有通用性.我們已經(jīng)計(jì)算了多種周期簇放電的PRC,至于周期簇放電神經(jīng)元的PRC與周期簇放電的分岔機(jī)理之間的關(guān)系將在今后的工作進(jìn)一步展開(kāi).本文的方波擾動(dòng)直接算法計(jì)算速度介于無(wú)限小擾動(dòng)的改進(jìn)算法和典型峰擾動(dòng)算法之間;在數(shù)值積分時(shí)積分步長(zhǎng)對(duì)計(jì)算結(jié)果有明顯的影響,當(dāng)積分步長(zhǎng)較大時(shí),PRC不準(zhǔn)確;當(dāng)積分步長(zhǎng)較小時(shí),則會(huì)增加計(jì)算時(shí)間.方波擾動(dòng)直接算法是從PRC定義出發(fā)設(shè)計(jì)的算法,計(jì)算過(guò)程中只需要確定方波擾動(dòng)幅值Ip和持續(xù)時(shí)間tp.而典型峰擾動(dòng)直接算法在計(jì)算時(shí)需要人為確定5個(gè)參數(shù)取值,并且方程還需增加一維.其他算法不是涉及伴隨方程求解就是特征方程求解,這一關(guān)鍵步驟在計(jì)算分岔機(jī)理比較復(fù)雜的周期簇放電的PRC時(shí)往往會(huì)求解失敗.這正是我們提出方波擾動(dòng)直接算法的原因.
[1]Hodgkin A L,Huxley A F 1952J.Physiol.117 500
[2]FitzHugh R 1961Biophys.J.1 445
[3]Nagumo J,Arimoto S,Yoshizawa S 1962Proc.IRE50 2061
[4]Morris C,Lecar H 1981Biophys.J.35 193
[5]Hindmarsh J L,Rose R M 1984Proc.R.Soc.London Ser.B221 87
[6]Xu L F,Li C D,Chen L 2016Acta Phys.Sin.65 240701(in Chinese)[徐泠風(fēng),李傳東,陳玲 2016物理學(xué)報(bào) 65 240701]
[7]Holden A V,Fan Y S 1992Chaos Soliton.Fract.2 221
[8]Holden A V,Fan Y S 1992Chaos Soliton.Fract.2 349
[9]Holden A V,Fan Y S 1992Chaos Soliton.Fract.2 583
[10]Fan Y S,Holden A V 1993Chaos Soliton.Fract.3 439
[11]Izhikevich E M 2000Int.J.Bifurcat.Chaos10 1171
[12]Gong P L,Xu J X 2001Phys.Rev.E63 031906
[13]Ding X L,Li Y Y 2016Acta Phys.Sin.65 210502(in Chinese)[丁學(xué)利,李玉葉 2016物理學(xué)報(bào) 65 210502]
[14]Gu H G,Zhu Z,Jia B 2011Acta Phys.Sin.60 100505(in Chinese)[古華光,朱洲,賈冰 2011物理學(xué)報(bào) 60 100505]
[15]Jin Q T,Wang J,Wei X L,Deng B,Che Y Q 2011Acta Phys.Sin.60 098701(in Chinese)[金淇濤,王江,魏熙樂(lè),鄧斌,車(chē)艷秋2011物理學(xué)報(bào)60 098701]
[16]Wang H X,Wang Q Y,Lu Q S 2011Chaos Soliton.Fract.44 667
[17]Yang Z Q,Guan T T,Gan C B,Zhang J Y 2011Acta Phys.Sin.60 110202(in Chinese)[楊卓琴,管亭亭,甘春標(biāo),張矯瑛2011物理學(xué)報(bào)60 110202]
[18]Longtin A 1993J.Stat.Phys.70 309
[19]Braun H A,Wissing H,Sch?fer K,Hirsch M C 1994Nature367 270
[20]Wiesenfeld K,Moss F 1995Nature373 33
[21]Yu Y,Wang W,Wang J,Liu F 2001Phys.Rev.E63 021907
[22]Liu F,Wang J,Wang W 1999Phys.Rev.E59 3453
[23]Ermentrout B 1996Neural Comput.8 979
[24]Gutkin B S,Ermentrout G B,Reyes A D 2005J.Neurophysiol.94 1623
[25]Hastings J W,Sweeney B M 1958Biol.Bull.115 440
[26]Johnson C H 1999Chronobiol.Int.16 711
[27]Ikeda N 1982Biol.Cybern.43 157
[28]Tsalikakis D G,Zhang H G,Fotiadis D I,Kremmydas G P,Michalis L K 2007Comput.Biol.Med.37 8
[29]Ermentrout G B,Kopell N 1991J.Math.Biol.29 195
[30]Ermentrout G B 1992SIAM J.Appl.Math.52 1665
[31]Stiger T,Danzl P,Moehlis J,Neto ffT I 2010J.Med.Devices4 027533
[32]Shi X,Zhang J D 2016Chin.Phys.B25 060502
[33]Schultheiss N W,Prinz A A,Butera R J 2012Phase Response Curves in Neuroscience(New York:Springer)p3
[34]Ermentrout G B 2002Simulating,Analyzing,and Animating Dynamical Systems:a Guide to XPPAUT for Researchers and Students(Philadelphia:SIAM)p226
[35]Govaerts W,Sautois B 2006Neural Comput.18 817
[36]Sherwood W E,Guckenheimer J 2010SIAM J.Appl.Dyn.Syst.9 659
[37]Novicenko V,Pyragas K 2011Nonlinear Dynam.67 517
[38]Ermentrout G B,Terman D H 2010Mathematical Foundations of Neuroscience(New York:Springer)p51
PACS:05.45.–a,87.19.ll,87.19.lnDOI:10.7498/aps.66.090501
A direct algorithm with square wave perturbation for calculating phase response curve?
Xie Yong?Cheng Jian-Hui
(State Key Laboratory for Strength and Vibration of Mechanical Structures,School of Aerospace,Xi’an Jiaotong University,
Xi’an 710049,China)
25 November 2016;revised manuscript
6 January 2017)
Neuron is a typical dynamic system,therefore,it is quite natural to study the fi ring behaviors of neurons by using the dynamical system theory.Two kinds of fi ring patterns,i.e.,the periodic spiking and the periodic bursting,are the limit cycle oscillators from the point of view of nonlinear dynamics.The simplest way to describe the limit cycle is to use the phase of the oscillator.A complex state space model can be mapped into a one-dimensional phase model by phase transformation,which is helpful for obtaining the analytical solution of the oscillator system.The response characteristics of the oscillator system in the motion state of the limit cycle to the external stimuli can be characterized by the phase response curve.A phase response curve illustrates the transient change in the cycle period of an oscillation induced by a perturbation as a function of the phase at which it is received.Now it is widely believed that the phase response curve provides a new way to study the behavior of the neuron.Existing studies have shown that the phase response curve of the periodic spiking can be divided into two types,which are closely related to the bifurcation mechanism of neurons from rest to repetitive fi ring.However,there are few studies on the relationship between the phase response curve and the bifurcation type of the periodic bursting.Clearly,the fi rst prerequisite to understand this relationship is to calculate the phase response curve of the periodic bursting.The existing algorithms for computing the phase response curve are often unsuccessful in the periodic bursting.In this paper,we present a method of calculating the phase response curve,namely the direct algorithm with square wave perturbation.The phase response curves of periodic spiking and periodic bursting can be obtained by making use of the direct algorithm,which is veri fi ed in the four neuron models of the Hodgkin-Huxley,FitzHugh-Nagumo,Morris-Lecar and Hindmarsh-Rose.This algorithm overcomes the limitations to other algorithms in the application.The calculation results show that the phase response curve of the periodic spiking is determined by the bifurcation type.We fi nd a suprathreshold periodic oscillation starting from a Hopf bifurcation and terminating at a saddle homoclinic orbit bifurcation as a function of the applied current strength in the Morris-Lecar model,and its phase response curve belongs to Type II.A large amount of calculation indicates that the relative size of the phase response and its positive or negative value depend only on the time of imposing perturbation,and the phase response curve of periodic bursting is more complicated than that of periodic spiking.
phase response curve,spiking,bursting,bifurcation
10.7498/aps.66.090501
?國(guó)家自然科學(xué)基金(批準(zhǔn)號(hào):11272241,11672219)資助的課題.
?通信作者.E-mail:yxie@mail.xjtu.edu.cn
*Project supported by the National Natural Science Foundation of China(Grant Nos.11272241,11672219).
?Corresponding author.E-mail:yxie@mail.xjtu.edu.cn
- 物理學(xué)報(bào)的其它文章
- 更正:分立式與分布式光纖傳感關(guān)鍵技術(shù)研究進(jìn)展[物理學(xué)報(bào) 2017,66(7):070705]
- 三階分布反饋太赫茲量子級(jí)聯(lián)激光器的遠(yuǎn)場(chǎng)分布特性?
- 以石墨烯為電極的有機(jī)噻吩分子整流器的設(shè)計(jì)及電輸運(yùn)特性研究?
- 基于雙平行馬赫-曾德?tīng)栒{(diào)制器的大動(dòng)態(tài)范圍微波光子下變頻方法?
- 等離子增強(qiáng)原子層沉積低溫生長(zhǎng)GaN薄膜?
- 基于Pareto優(yōu)化理論的多目標(biāo)超橢梯度線圈設(shè)計(jì)?

