一種基于決策森林的單調分類方法
許 行 王文劍,2 任麗芳,3
1(山西大學計算機與信息技術學院 太原 030006)2(計算智能與中文信息處理教育部重點實驗室(山西大學) 太原 030006)3 (山西財經大學應用數學學院 太原 030006)
?
一種基于決策森林的單調分類方法
許 行1王文劍1,2任麗芳1,3
1(山西大學計算機與信息技術學院 太原 030006)2(計算智能與中文信息處理教育部重點實驗室(山西大學) 太原 030006)3(山西財經大學應用數學學院 太原 030006)
(xuh102@126.com)
單調分類問題是特征與類別之間帶有單調性約束的有序分類問題.對于符號數據的單調分類問題已有較好的方法,但對于數值數據,現有的方法分類精度和運行效率有限.提出一種基于決策森林的單調分類方法(monotonic classification method based on decision forest, MCDF),設計采樣策略來構造決策樹,可以保持數據子集與原數據集分布一致,并通過樣本權重避免非單調數據的影響,在保持較高分類精度的同時有效提高了運行效率,同時這種策略可以自動確定決策森林中決策樹的個數.在決策森林進行分類時,給出了決策沖突時的解決方法.提出的方法既可以處理符號數據,也可以處理數值數據.在人造數據集、UCI及真實數據集上的實驗數據表明:該方法可以提高單調分類性能和運行效率,縮短分類規則的長度,解決數據集規模較大的單調分類問題.
單調分類;決策樹;單調一致性;決策森林;集成學習
單調分類是一種特殊的分類問題,廣泛存在于實際生活中,如大學綜合水平的評定問題,其中“科研水平”、“師資隊伍”、“教學質量”是3個重要指標,其得分很顯然就是一種序關系,大學綜合水平的“評定等級”若為“高、中、低”,則它們之間也具有優劣次序,這一問題的特征(科研水平、師資隊伍、教學質量)與類別(評定等級)之間存在以下單調性約束:當一所學校在科研水平、師資隊伍、教學質量這3個特征上的分數都不比另一所學校低時,它的評定等級就一定不會比另一所學校低.此外,還有諸如決策風險分析、企業績效考核、消費者滿意度評價等問題都具有同樣的特點,這類問題就是單調分類問題.與一般分類問題不同,單調分類問題的特征與類別上的取值都存在序的關系,且2者之間滿足單調性約束.
對于一般的分類問題,已經有很多分類方法,如決策樹、神經網絡、支持向量機等,這些方法一般不考慮特征與類別上的序關系,所以不能得到單調一致的分類規則.目前對于單調分類問題已有一些研究,如以粗糙集為理論框架的模型解決單調分類問題[1-6],但這些方法獲得的單調一致的分類規則數量有限,且只能用于符號數據.對于數值數據的單調分類問題,我國學者Hu等人[7-10]提出的單調決策樹是目前較好的方法,他們在一定程度上解決了單調性和泛化能力之間的沖突,還將序的關系引入經典Shannon熵,提出有序信息熵概念,并在此基礎上設計了基于有序信息熵的決策樹算法(rank entropy based monotonic decision tree, REMT).這種方法能夠產生結構簡單、易于理解的規則集,但得到的精度相對有限,且存在過度擬合問題.
決策森林源于隨機森林[11],是以決策樹為基礎分類器的集成算法,可以有效避免過度擬合,且能夠提高分類精度,因而受到了研究者的廣泛關注.但決策森林目前只用于解決一般的分類問題,對于單調分類問題,構造決策森林時面臨3種困難:1)單個決策樹的構造需要在不同的訓練子集上進行,如何保證子集的單調性;2)如何確定決策森林的規模;3)集成規則出現沖突時如何解決.
本文提出一種用于解決單調分類問題的基于決策森林的單調分類方法,設計采樣策略來構造決策樹,該策略考慮數據集單調一致的特點,可避免非單調數據的噪聲影響,同時這種策略可以自動確定決策森林中決策樹的個數.在決策森林進行分類時,本文還提出葉子節點上的規則支持度的概念,從而給出決策沖突時的解決方法.本文提出的方法既可以處理符號數據,也可以處理數值數據.
1 背景知識
1.1 單調分類問題
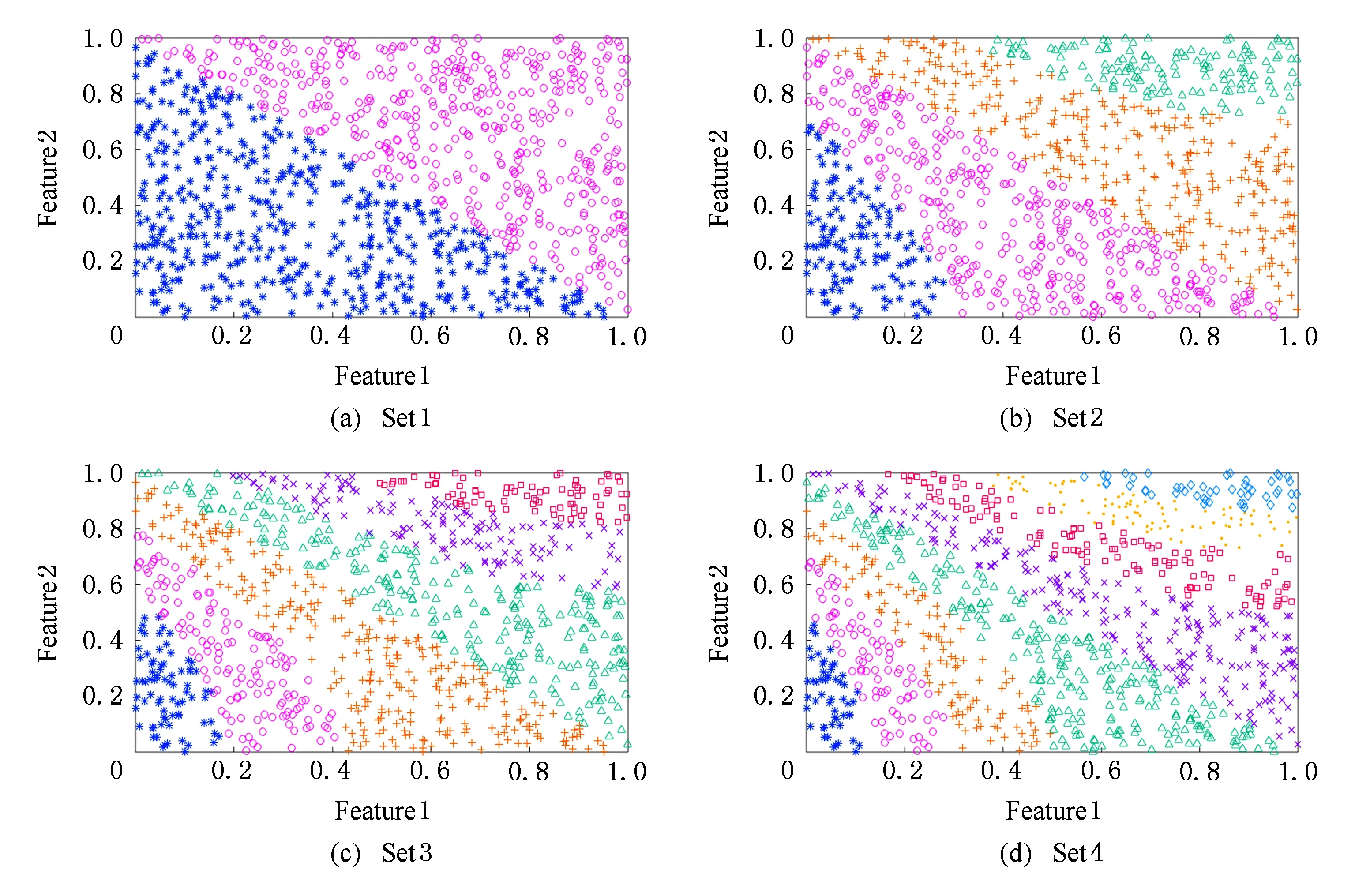
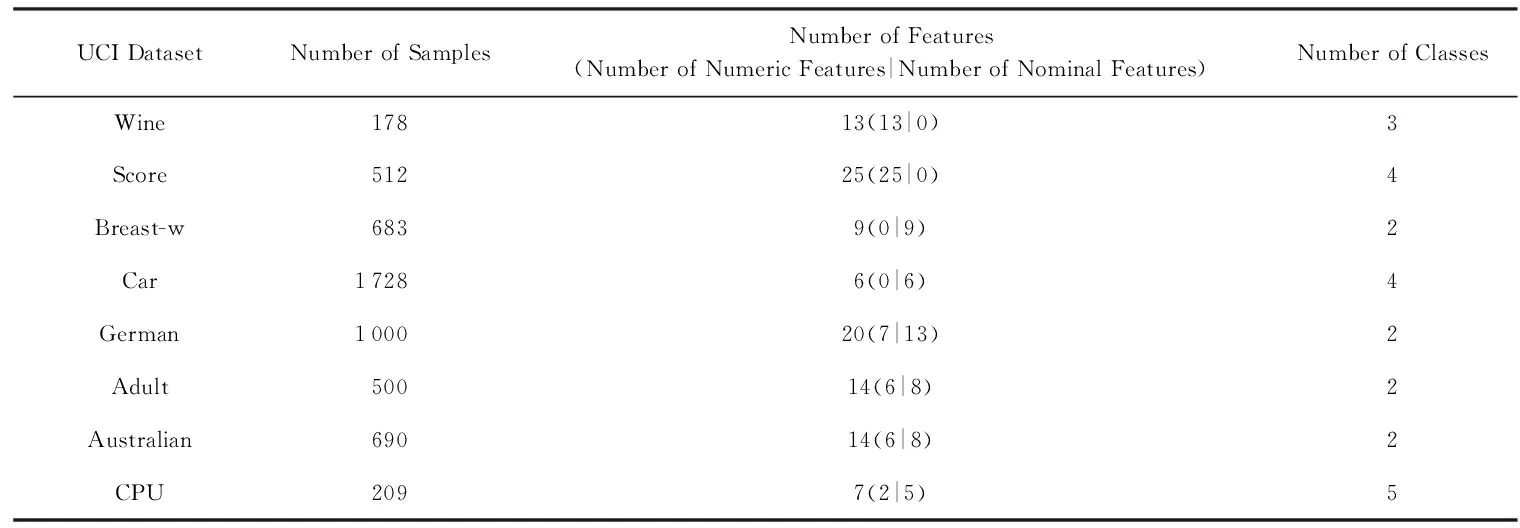
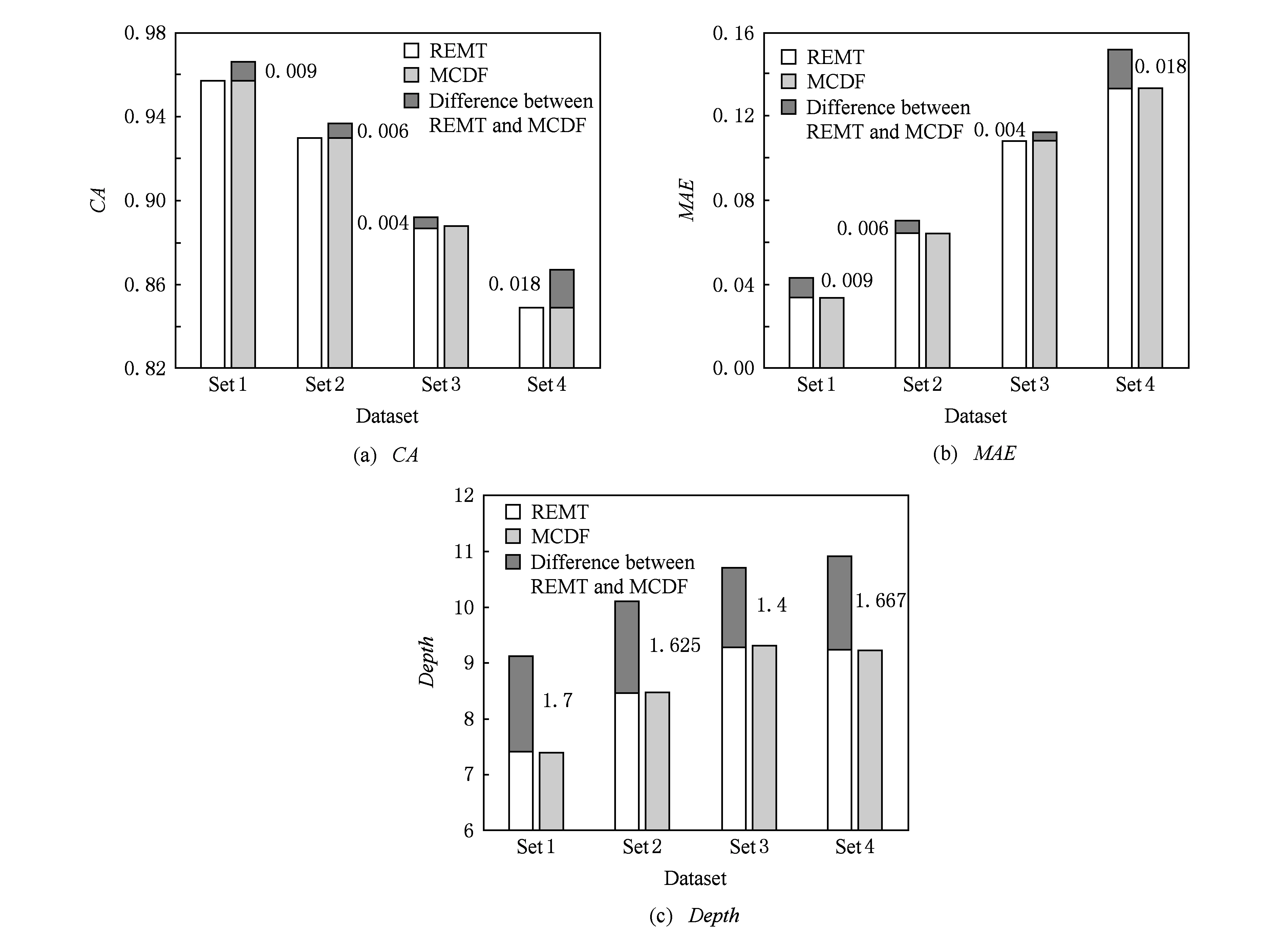
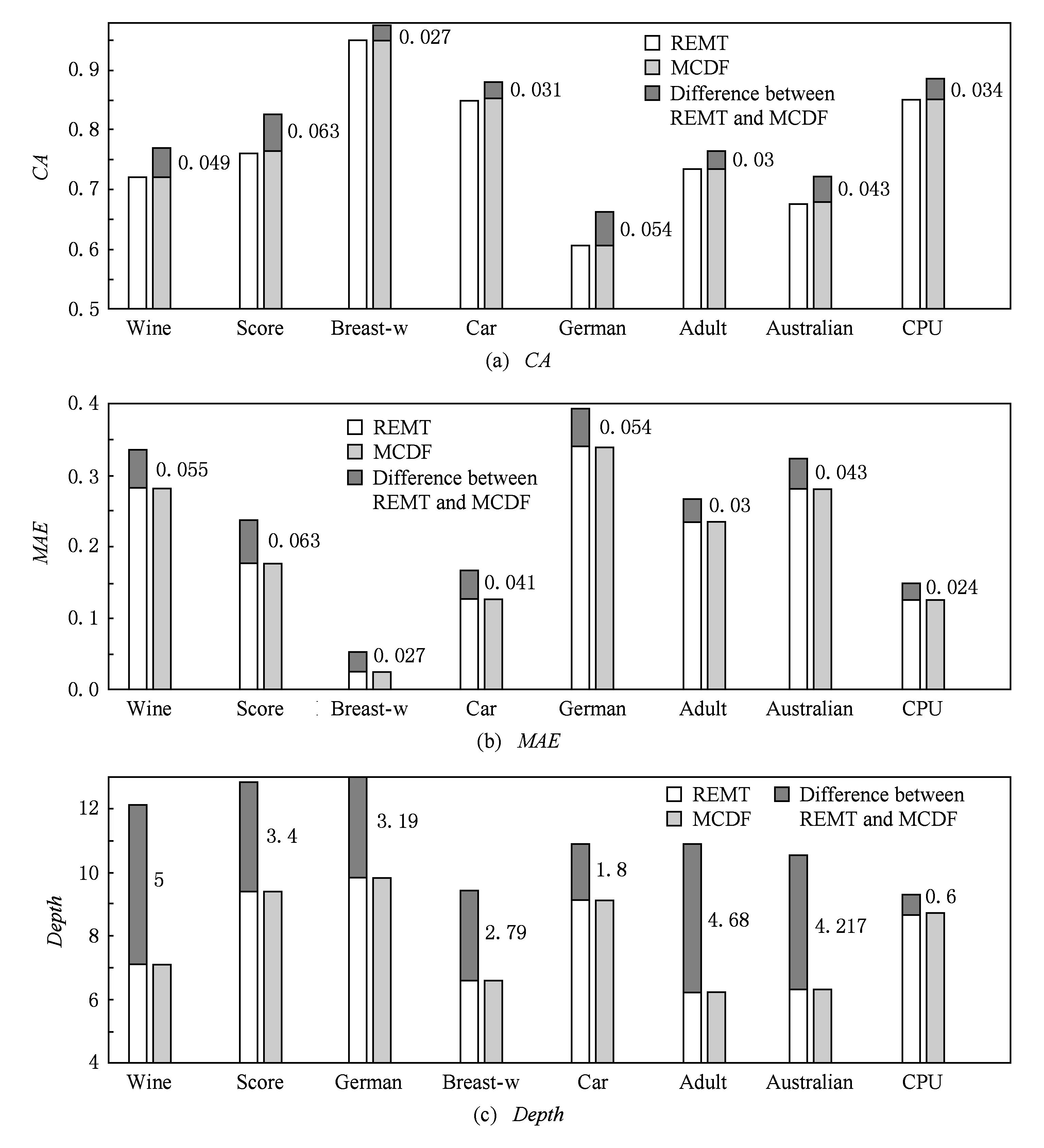
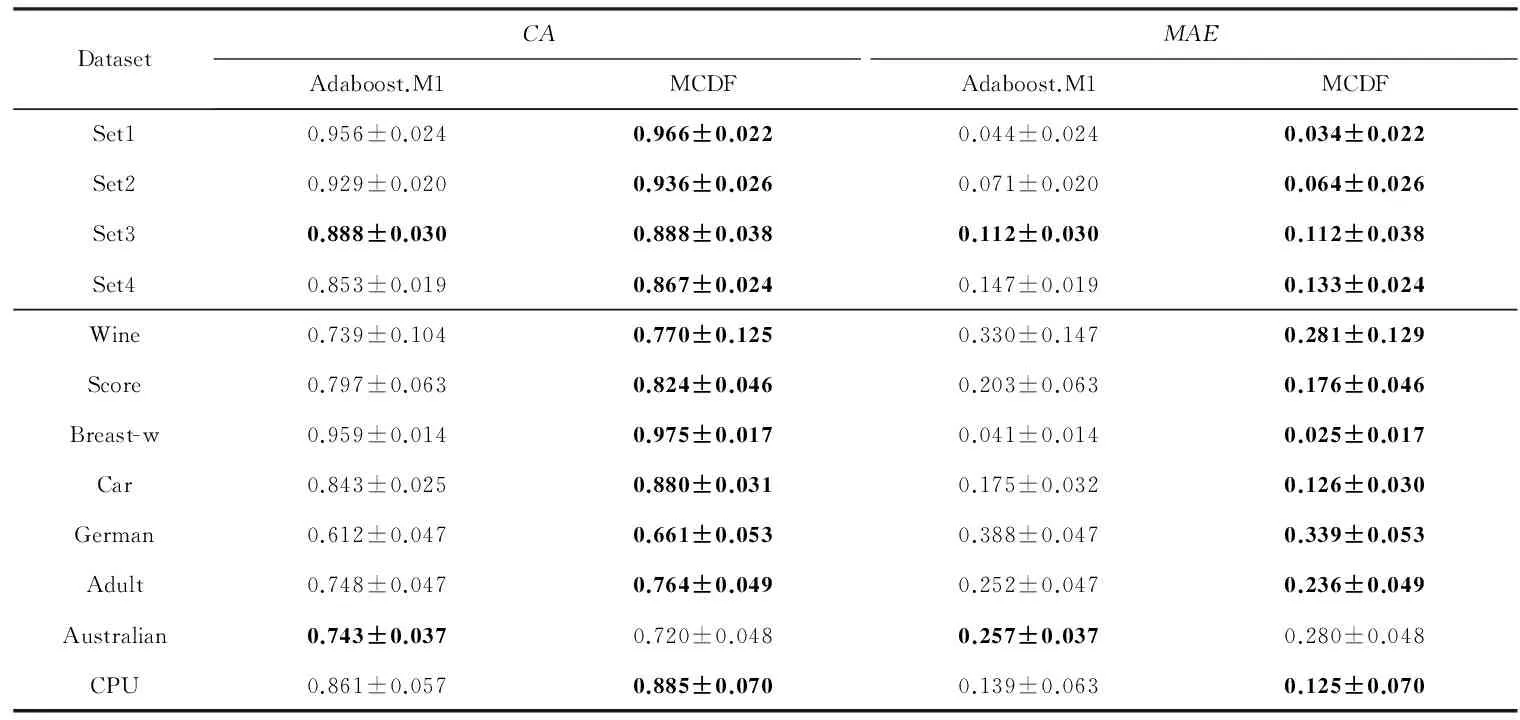
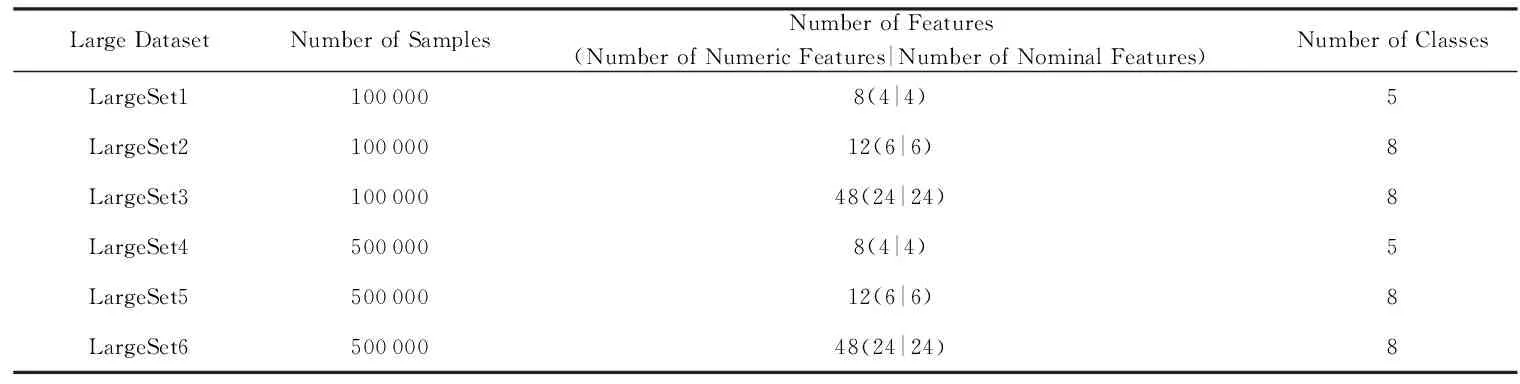
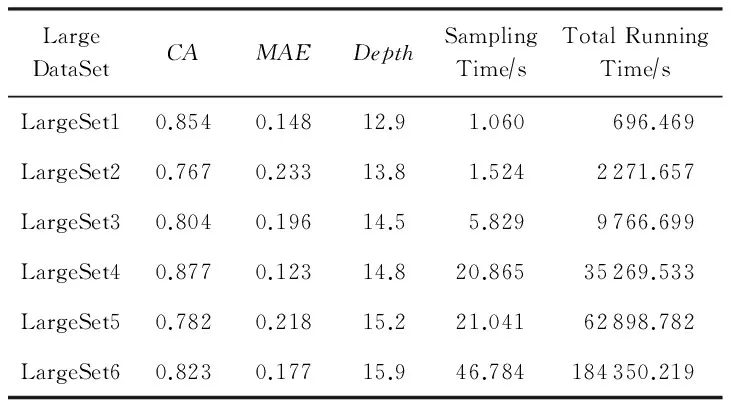
令U={x1,x2,…,xn}為數據集,A={a1,a2,…,am}是描述數據的特征集,xi在特征a上的值記為a(xi),xi的類標簽記為y(xi).如果y(xi)的值域{c1,c2,…,cs}上存在序關系c1 對于一個有序分類問題,如果?xi,xj∈U在每一個特征ak∈A上都滿足若ak(xi)≤ak(xj),則y(xi)≤y(xj),那么該問題為單調分類問題[12]. 給定xi∈U,若特征集B?A,則在特征集B上xi的優勢類和劣勢類分別定義為 (1) (2) 1.2 決策森林 決策森林是由多個單棵決策樹組成集成分類器的集成學習方法,可表示為{h(x,θk),k=1,2,…},其中,x是輸入樣本,θk是獨立同分布的隨機變量,h(x,θk)表示一棵決策樹.對于輸入樣本x,每棵決策樹判斷其類別后投票給與其判斷結果相符的類,得票最多的一類為最終分類結果.構建決策森林的方式主要有基于數據集的構造方式和基于特征集的構造方式. 構建決策森林模型時主要考慮4方面: 1) 當采用基于數據集的構造方式構造決策森林時,訓練數據子集如何構成; 2) 當采用基于特征集的構造方式構造決策森林時,特征子集如何構成; 3) 決策樹的數目如何確定; 4) 生成的所有決策樹如何集成為決策森林模型. 2.1 單棵決策樹的構造 決策森林的預測能力與每棵決策樹相關,為用較少的決策樹構造出精度較高的決策森林,決策樹必須要有一定的差異性.本文采用基于數據集的構造方式構造決策森林,通過為每個決策樹構造有差異性的訓練子集來獲得決策樹之間的差異性.構造單棵決策樹的訓練子集時,不能采用經典的隨機采樣、bagging[13]、boosting[14]等方法,因為隨機采樣和bagging方法都不考慮數據的分布情況,boosting方法對噪聲的敏感性使其更易于產生過擬合現象[15],并且這些方法也沒有考慮數據的單調性.Liang等人[16]提出一種較好的重采樣方法,使得采樣得到的子集間有一定的差異度又能較大程度地覆蓋原始數據集,且與原數據集分布相同,但該方法不考慮數據的序關系,且只能用于符號數據的處理. 本文借鑒文獻[16],將以上方法引入單調分類問題,可以同時處理符號數據和數值數據.在構造單棵決策樹時,為保持單調分布的一致性,為每個樣本加權,在多次采樣時權值不是固定不變的,而是隨著已有決策樹的錯誤率和錯分樣本的單調一致性進行調整,在調整中去掉不一致的樣本.另外,本文中訓練子集的規模不是由用戶指定的固定值,而是根據數據集的特征自動確定的. 1) 訓練子集規模的確定 對于數據集U,文獻[16]給出的訓練子集規模M為 (3) 其中,Z為置信水平下的Z-統計值,可以計算得出,E為可以接受的誤差,由用戶指定,這2個變量取值已知,因此計算M的關鍵在于數據集上的標準差σ的計算.文獻[16]給出了符號數據上σ的計算方法. 為同時處理符號數據和數值數據,本文設計的標準差σ為 (4) 對于數值型特征,先統一各個特征的取值范圍,將所有樣本的特征取值歸一化: (5) 其中,akmin(x)和akmax(x)分別表示所有樣本在特征ak上的最小值和最大值,然后計算該特征的特征標準差: 對于符號型特征,與文獻[16]不同,本文采用單個特征的不相似度而不是基于所有特征上的不相似度來計算特征標準差σak. (7) 一般地,為保證學習器的訓練效率,訓練子集的規模M不宜太大,若M與樣本總數N超過一定比率θ(如θ=5%),需要調整訓練子集的規模,調整方法為 (8) 確定訓練子集樣本的規模算法總結如下. 算法1. 確定訓練子集樣本的規模算法. 輸入: 單調數據集U、參數Z,E,θ; 輸出: 訓練子集的規模M. Step1. 按式(4)計算數據集的標準差:若特征為數值型,則按式(5)將所有樣本在該特征上的取值歸一化,然后按式(6)計算其特征標準差;若特征為符號型,則按式(7)計算其特征標準差; Step2. 按式(3)計算訓練子集的規模M; Step4. 返回M. 2) 訓練子集的采樣 采樣訓練子集前,先計算原始訓練集U中每個類別的樣本占所有樣本的比例pl: (9) 其中,l=1,2,…,s,Cl={xi∈U|y(xi)=cl},i=1,2,…,n.采樣時要確保各個類別的樣本數在原訓練集與采樣出的訓練子集中的比例相同.之后通過迭代采樣訓練子集,每次迭代產生1個訓練子集.迭代過程如下: 初始狀態下,原訓練集U中所有樣本的權重相等,即每個樣本的初始權重為 (10) 其中,n為原訓練集中樣本的數量. 首先采樣第1個訓練子集U1,在原訓練集U中隨機選擇M個樣本,并保證其中每個類別的樣本數與M的比例為pl,l=1,2,…,s.采樣下一個訓練子集Ut時,先在前一個訓練子集上生成決策樹,計算該決策樹的加權誤差εt: (11) 根據錯誤率更新原訓練集的樣本權重:對于錯分的樣本,首先判斷該樣本的單調一致性,本文用包含度描述樣本的單調一致性.定義xi在特征集A與類標簽y上的包含度為 (12) D(xi)的值越大,表示樣本xi在特征集與類別上取值的單調一致性越高.這里把滿足D(xi)≥e的樣本xi看作單調一致的樣本,否則為非單調一致的樣本,e為給定的參數. 對于錯分的單調一致樣本,增加其權重: (13) 對于錯分的非單調一致樣本,減小其權重:因為非單調一致的樣本會影響分類器的精確度,故令其權重直接為0. 由于每次迭代產生1個訓練子集,每個訓練子集對應生成1棵決策樹,因此迭代執行的次數就是決策森林中決策樹的數目.當M確定后,每次從未抽取過的數據集中抽取的樣本個數(1-α)M也隨之確定,進而可以確定總迭代次數.也就是說,決策森林中決策樹的數目可以通過確定每個訓練子集的樣本規模自動確定. 訓練子集的采樣算法總結如下. 算法2. 訓練子集的采樣算法. 輸入: 單調數據集U、參數Z,E,θ,e,α; 輸出:h個訓練子集. Step1. 用算法1確定訓練子集的樣本規模M. Step2. 對于單調數據集U,按式(9)計算其中各個類別的比例pl; Step3. 按式(10)為訓練集中每個樣本的權重賦初值; Step4. 在U上隨機選擇訓練子集U1,并保證其中各類別樣本數占該訓練子集中所有樣本數的相應比例為pl; Step5. 按以下步驟,迭代生成決策樹,直到訓練集U上未被抽取的樣本數小于M時結束循環,并記錄迭代執行的次數h; Step5.1. 在上一訓練子集上用REMT[9]方法生成決策樹,并按式(11)計算決策樹的加權誤差; Step5.2. 對錯分樣本按式(12)計算其單調一致性,對給定參數e,若D(xi)≥e,則按式(13)更新xi的權重,否則權重為0; Step5.3. 在Ut-1上抽取αM個樣本,在U上未被抽取的樣本中抽取(1-α)M個樣本,得到新的訓練子集Ut,并保證其各類別的相應比例為pl; Step5.4. 對Ut中的樣本權重歸一化; Step6. 返回h個訓練子集Ut(t=1,2,…,h). 在每個訓練子集Ut上,采用適用于單調分類的REMT算法[9]可以生成單棵決策樹Tt,t=1,2,…,h. 2.2 決策森林的生成算法 本文提出一種基于決策森林的單調分類算法(monotonic classification method based on decision forest, MCDF),通過計算每棵決策樹的規則支持度,獲得決策森林最終的分類結果. 對于每棵決策樹,設葉子節點leafi中包含的樣本集為Uleafi,這些樣本來自不同的類c1,c2,…,定義分類規則在類別ck上的規則支持度為 (14) 其中,Uleafi k表示葉子節點leafi中的第k類樣本集. 規則支持度Support(ck)記錄在每棵決策樹的每個葉子節點上,集成決策樹時,根據每棵樹的分類規則和規則支持度確定分類結果:當一個新的樣本輸入時,讓每棵決策樹根據自己的分類規則對其投票,即投票給它認為正確的類別,最后選擇得票數最多的類作為該樣本的最終分類結果.若有r個類別的得票數相等(r≥2),即決策沖突時,計算每棵決策樹中用于判斷該樣本類別的葉子節點的規則支持度,將這h棵決策樹在每種類別上的規則支持度加和,取規則支持度之和最大的類別作為該樣本的最終分類結果,即該樣本的分類結果為 (15) 本文提出的MCDF算法的主要步驟如下. 算法3. MCDF算法. 輸入: 訓練集UTrain、測試集UTest、參數Z,E,θ,e,α; 輸出: 測試集UTest中所有樣本的分類結果. Step1. 用算法2得到訓練集UTrain的h個訓練子集Ut,t=1,2,…,h; Step2. 在每個訓練子集上用決策樹算法REMT[9]生成決策樹Tt,t=1,2,…,h,按式(14)計算每個葉子節點中各個類別上的規則支持度; Step3. 對測試集中的一個樣本x,讓h棵決策樹對其分類并投票,得到多個分類結果ck,k=1,2,…; Step4. 比較每個類別ck的得票數,按以下步驟決定最終分類結果: Step4.1. 若具有最多票數的ck唯一,記為cmax,則cmax就是該樣本的最終類別; Step4.2. 若同時具有最多票數的類別ck有r個(r≥2),則按式(15)計算這r個類中規則支持度之和最大的類別ck,作為該樣本的最終類別; Step5. 對測試集UTest中的所有樣本分類后返回分類結果. 2.3 時間復雜度分析 由于決策樹數目可以提前計算,因此,MCDF方法構建決策森林的時間主要由采樣時間和生成決策樹的時間2部分構成. 采樣過程中,樣本在特征集與類標簽上的包含度可以在采樣前提前計算,不需占用采樣時間.而計算決策樹的加權誤差、更新樣本權重和抽樣過程都需要分別遍歷1次M個樣本,因此單棵決策樹的采樣過程的時間復雜度為O(M). 生成決策樹時,需要分別考慮非葉子節點和葉子節點上的時間復雜度. 2) 在第j個葉子節點上,需要遍歷該節點中的所有樣本求其所包含的每個類別的支持度,故葉子節點上的時間復雜度為O(nj)≤O(M). 假設決策森林中的非葉子節點和葉子節點數分別為k1和k2,則生成決策樹的時間復雜度為O(k1mvM2+k2M). 綜上,設MCDF方法構建的決策森林中決策樹數目為h個,那么MCDF方法的時間復雜度為O(hM+k1mvM2+k2M). 由以上分析可知,本方法中雖然增加了采樣過程,但采樣的時間復雜度僅為O(hM),而通過采樣可以將時間復雜度中的樣本數量M由原訓練集的樣本數量n減少為采樣后的M,而M?n. 3.1 實驗數據集及評價指標 本文分別在4個人造數據集、7個UCI及1個真實數據集上進行實驗.4個單調的人造數據集構造[8]為 (16) 其中,x1,x2∈[0,1]. 每個數據集都有1 000個樣本、2個特征,類別數依次為2類、4類、6類和8類,其散點圖如圖1所示: Fig. 1 The artificial datasets圖1 人造數據集 本文還使用表1所示的8個數據集驗證算法,除Score為山西大學學生成績的真實數據集外,剩下的7個為UCI數據集.其中Wine,Score為數值型數據集,Breast-w,Car為符號型數據集,其他4個為既包含符號型特征也包含數值型特征的數據集. Table 1 The Datasets Description表1 數據集描述 在每個數據集上進行十折交叉驗證.使用分類準確率和平均絕對誤差作為預測能力的評價標準. 分類準確率CA定義為 (17) 平均絕對誤差MAE定義為 (18) 此外,用決策樹的平均深度Depth作為分類規則長度的評價標準.實驗設備是1臺配置為3.60 GHz-4核CPU、8 GB內存的計算機,實驗平臺是MyEclipse 2015CI.相關參數設置如下:Z=1.96,E=1.2,θ=0.05,e=0.1,α=0.5. 3.2 MCDF與REMT算法的比較 Hu等人提出的REMT單調分類算法[9]是單調分類問題中較為經典的算法,因此本文首先比較MCDF與REMT單調分類算法的分類精度、平均絕對誤差和決策樹深度. 圖2和圖3分別為2種算法在人造數據集和UCI及真實數據集上的實驗結果. 從圖2和圖3可以看出,除人造數據集Set3以外,MCDF方法在所有數據集上都比REMT算法的分類準確率高,平均絕對誤差低;由于訓練子集的規模比原訓練集的規模小,所以在包括Set3在內的所有數據集上,MCDF方法都比REMT算法的決策樹深度小. Fig. 2 The experimental result comparison of REMT and MCDF on the artificial datasets圖2 人造數據集上REMT算法與MCDF方法的實驗結果比較 在人造數據集Set3上,MCDF方法在CA和平均絕對誤差MAE上比REMT算法低約0.4%.MCDF方法在生成多個決策樹的迭代過程中,除了每次采樣不同的訓練樣本外,還通過判斷錯分樣本的單調一致程度來改變每棵決策樹中訓練樣本的權重,以增加各個決策樹之間的差異度,從而提高決策森林的分類精度.而由于構造的人造數據集具有較強的單調一致性,一方面單調一致的數據集中不會有權重為0的樣本出現,另一方面,單棵決策樹在單調一致的數據集上每次迭代得到的錯分樣本數量較少,即權重改變的樣本數較少,造成了各個決策樹之間的樣本權重差異度不大,所以MCDF方法的優越性沒有得到充分體現;而REMT算法由于使用了全部的訓練對象,在人造數據集上具有較好的分類性能.實際上,在人造數據集上,2種方法的分類性能差別不大:在Set1,Set2,Set4上MCDF方法精度比REMT算法提高不多(分別為0.9%,0.6%和1.8%),在Set3上低于REMT算法的差距也很小(0.4%). 根據實驗結果,在人造數據集和UCI及真實數據集上,MCDF方法比REMT算法的分類準確率分別平均提高了0.72%和4.14%,平均絕對誤差分別平均降低了0.73%和4.21%,而且由于使用了較小規模的訓練子集,MCDF方法得到的決策樹深度在人造數據集和UCI及真實數據集上分別平均減少了1.6和3.21,因此本文提出的方法可以提高單調分類的性能,縮短分類規則的長度. Fig. 3 The experimental result comparison of REMT and MCDF on the UCI and real datasets圖3 UCI及真實數據集上REMT算法與MCDF方法的實驗結果比較 3.3 MCDF與Adaboost.M1算法的比較 MCDF與經典的集成學習方法Adaboost.M1算法[14]進行了比較,表2是2種方法在12個數據集上的準確率和平均絕對誤差比較. 從表2可以看出,除Australian以外的其他11個數據集上,MCDF比Adaboost.M1的分類準確率高、平均絕對誤差低.因為Adaboost.M1算法是根據基分類器的錯誤率改變錯分的訓練樣本的權重,進而構造不同的訓練子集,生成決策樹,而對于單調分類問題,由于訓練集中存在非單調一致的樣本,在Adaboost.M1算法的迭代過程中,這些樣本的權重逐漸增大,降低了基分類器的準確率,使得Adaboost.M1算法的集成結果較差.而本文算法中根據D(xi)判斷樣本xi的單調一致性,避免采樣非單調一致的樣本,同時提高采樣得到的訓練子集的差異性,所以取得了較好的集成效果. 在數據集Australian上,MCDF方法在CA和平均絕對誤差MAE上都比Adaboost.M1算法低2.3%,其原因首先與數據集Australian本身的特點有關.根據文獻[12]中有序數據集上特征對類別的依賴度的定義可以求得:數據集Australian上的特征依賴度為0.998,接近于1,也就是說幾乎所有樣本都可以被一致地分配類別,這與人造數據集上的情況相似.其次,MCDF方法在數據集Australian上的迭代過程中較少出現權重改變較大的樣本,降低了MCDF方法創建的決策森林中各個決策樹之間的差異度,使得MCDF方法的性能受到影響;而數據集Australian中噪聲較少的特點恰好避開了Adaboost.M1算法對噪聲比較敏感的弱點,使其分類效果不受影響.另外,數據集Australian的類別數為2,也使得MCDF方法針對多類別之間的有序關系上的優勢難以得到體現,而Adaboost.M1每次都使用了全部訓練樣本生成決策樹,具有相對較好的分類性能.以上3個因素共同造成了MCDF在Australian上的分類性能略差于Adaboost.M1算法.但是與Set3一樣,雖然MCDF方法的分類精度比Adaboost.M1略有下降,但其運行效率比Adaboost.M1算法高. Table 2 The CA and MAE Result Comparison of Adaboost.M1 and MCDF on the Datasets表2 Adaboost.M1算法與MCDF方法的準確率和誤差比較 3.4 REMT,Adaboost.M1與MCDF的運行時間 REMT,Adaboost.M1與MCDF方法在運行時間上進行了比較,表3是3種方法在12個數據集上的實驗結果. Table 3 The Running Time Comparison of REMT, Adaboost.M1 and MCDF表3 REMT,Adaboost.M1與MCDF方法的運行 時間比較 s 從表3可以看出,運行效率上,MCDF方法的執行時間比REMT算法、Adaboost.M1算法都有很大提高,尤其在數值型數據集上,如Set1~Set4,效果非常顯著.按照2.3節中的分析可知,生成每棵決策樹的時間復雜度為O(k1mvM2+k2M),由于Set1~Set4為數值型數據集,所以其特征的值域取值有ni種,即v=ni,以根節點為例,數值型數據集根節點上的時間復雜度就為O(mM3),那么與REMT和Adaboost.M1算法每次都使用訓練集中的所有對象生成單棵決策樹相比,如果MCDF方法的樣本量減少為原來的20%,根節點上的運行時間就可以減少為原來的1500,同理,其他節點上的運行時間也都有不同程度的降低,而采樣過程所增加的時間花銷卻很小.因此,盡管REMT算法只訓練1棵決策樹,但其時間復雜度為2n),而M?n,所以其運行速度仍然比MCDF方法慢,而Adaboost.M1算法所需時間為REMT的hA倍(hA為Adaboost.M1算法構造的基分類器數量),運行速度更慢.由實驗結果可知,在數值型的人造數據集上,MCDF方法的平均時間花銷分別約為REMT和Adaboost.M1算法的19和1130;在UCI及真實數據集上,MCDF方法的平均時間花銷提高最多的是German數據集,分別約為REMT和Adaboost.M1的15和155,即使在提高最少的CPU數據集上,MCDF方法的時間花銷也僅約為REMT和Adaboost.M1的12和114.因此,本文提出的方法有效地提高了運行效率. 3.5 MCDF在較大規模數據集上的有效性 由于UCI中單調數據集的規模較小,為了驗證MCDF在較大規模數據集上的有效性,用以下函數構造單調數據集: f(x1,x2,…,xm)= (19) Table 4 The Large Dataset Description表4 大規模數據集描述 在該數據集上,MCDF方法的實驗結果如表5所示.而REMT和Adaboost.M1算法在數據集LargeSet1,LargeSet2上用MCDF方法的10倍運行時間仍無法得到結果;在LargeSet3~LargeSet6這4個數據集上,也無法在可接受的時間內得到結果. Table 5 The Experimental Result on the Large Dataset表5 大規模數據集實驗結果 本文提出的MCDF方法針對單調的數據集,用基于數據集的構造方式構建決策森林,解決單調分類問題.該方法既可處理符號型數據,又可處理數值型數據以及包含符號型和數值型的混合數據;設計的采樣策略,在保持較高分類精度的同時大大提高了運行效率;提出的規則支持度有效地保證了單調分類的性能;此外,該方法還可以解決大規模數據集上的單調分類問題.本文通過數據集各個特征上的取值來自動確定決策樹的數目,可以避免人工干預,但需要遍歷所有樣本來獲得對決策樹的評價,對算法效率有一定影響.能否根據決策樹本身的結構選擇部分決策樹來構成決策森林還需要進一步研究. [1]Greco S, Matarazzo B, Slowinski R. Rough approximation by dominance relations[J]. International Journal of Intelligent Systems, 2002, 17(2): 153-171 [2]Sai Ying, Yao Yiyu, Zhong Ning. Data analysis and mining in ordered information tables[C]Proc of IEEE ICDM’01. Los Alamitos, CA: IEEE Computer Society, 2001: 497-504 [3]Kotlowski W, Dembczynski K, Greco S, et al. Stochastic dominance based rough set model for ordinal classification[J]. Information Sciences, 2008, 178(21): 4019-4037 [4]Hu Qinghua, Yu Daren, Guo Maozu. Fuzzy preference based rough sets[J]. Information Sciences, 2010, 180(10): 2003-2022 [5]Qian Yuhua, Dang Chuangyin, Liang Jiye, et al. Set-valued ordered information systems[J]. Information Sciences, 2009, 179(16): 2809-2832 [6]Ben-David A. Automatic generation of symbolic multiattribute ordinal knowledge-based DSSs: Methodology and applications[J]. Decision Sciences, 1992, 23(6): 1357-1372 [7]Hu Qinghua, Guo Maozu, Yu Daren, et al. Information entropy for ordinal classification[J]. Science China: Information Sciences, 2010, 53(6): 1188-1200 [8]Hu Qinghua, Pan Weiwei, Zhang Lei, et al. Feature selection for monotonic classification[J]. IEEE Trans on Fuzzy Systems, 2012, 20(1): 69-81 [9]Hu Qinghua, Che Xunjian, Zhang Lei, et al. Rank entropy based decision trees for monotonic classification[J]. IEEE Trans on Knowledge and Data Engineering, 2012, 24(11): 2052-2064 [10]Che Xunjian. Ordinal decision tree based fault level detection[D]. Harbin: Harbin Institute of Technology, 2011 (in Chinese)(車勛建. 基于有序決策樹的故障程度診斷研究[D]. 哈爾濱: 哈爾濱工業大學, 2011) [11]Breiman L. Random forest[J]. Machine Learning, 2001, 45(1): 5-32 [12]Hu Qinghua, Yu Daren. Applied Rough Computing[M]. Beijing: Science Press, 2012 (in Chinese)(胡清華, 于達仁. 應用粗糙計算[M]. 北京: 科學出版社, 2012) [13]Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140 [14]Freund Y, Schapire R E. A decision-theoretic generalization of on-line learning and an application to boosting[J]. Journal of Computer and System Sciences, 1997, 55(1): 119-139 [15]Wang Wenjian, Men Changqian. Support Vector Machine Modeling and Application[M]. Beijing: Science Press, 2014 (in Chinese)(王文劍, 門昌騫. 支持向量機建模及應用[M]. 北京: 科學出版社, 2014) [16]Liang Jiye, Wang Feng, Dang Chuangyin, et al. An efficient rough feature selection algorithm with a multi-granulation view[J]. International Journal of Approximate Reasoning, 2012, 53(6): 912-926 Xu Hang, born in 1987. PhD candidate. Her main research interests include machine learning and service computing. Wang Wenjian, born in 1968. PhD. Professor, PhD supervisor. Senior member of CCF. Her main research interests include neural networks, support vector machine, machine learning and intelligent computing. Ren Lifang, born in 1976. PhD candidate. Lecturer. Her main research interests include machine learning and service computing. A Method for Monotonic Classification Based on Decision Forest Xu Hang1, Wang Wenjian1,2, and Ren Lifang1,3 1(SchoolofComputerandInformationTechnology,ShanxiUniversity,Taiyuan030006)2(KeyLaboratoryofComputationalIntelligenceandChineseInformationProcessing(ShanxiUniversity),MinistryofEducation,Taiyuan030006)3(SchoolofAppliedMathematics,ShanxiUniversityofFinanceandEconomics,Taiyuan030006) Monotonic classification is an ordinal classification problem in which the monotonic constraint exists between features and class. There have been some methods which can deal with the monotonic classification problem on the nominal datasets well. But for the monotonic classification problems on the numeric datasets, the classification accuracies and running efficiencies of the existing methods are limited. In this paper, a monotonic classification method based on decision forest (MCDF) is proposed. A sampling strategy is designed to generate decision trees, which can make the sampled training data subsets having a consistent distribution with the original training dataset, and the influence of non-monotonic noise data is avoided by the sample weights. It can effectively improve the running efficiency while maintaining the high classification performance. In addition, this strategy can also determine the number of trees in decision forest automatically. A solution for the classification conflicts of different trees is also provided when the decision forest determines the class of a sample. The proposed method can deal with not only the nominal data, but also the numeric data. The experimental results on artificial, UCI and real datasets demonstrate that the proposed method can improve the monotonic classification performance and running efficiency, and reduce the length of classification rules and solve the monotonic classification problem on large datasets. monotonic classification; decision tree; monotonic consistency; decision forest; ensemble learning 2016-03-11; 2016-08-08 國家自然科學基金項目(61673249,61503229);山西省回國留學人員科研基金項目(2016-004);山西省研究生教育創新項目(2016BY003) This work was supported by the National Natural Science Foundation of China (61673249, 61503229), the Scientific Research Foundation for Returned Scholars of Shanxi Province (2016-004), and the Innovation Project of Shanxi Graduate Education (2016BY003). 王文劍(wjwang@sxu.edu.cn) TP181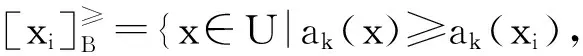
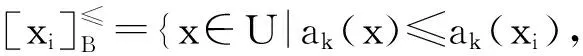
2 決策森林單調分類方法
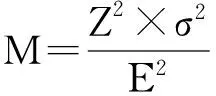

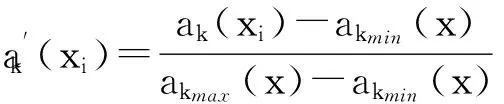
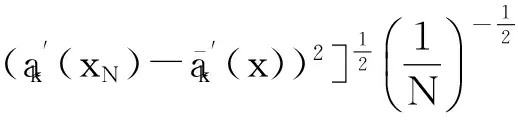
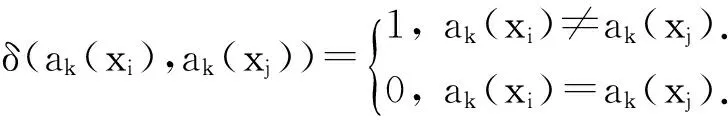
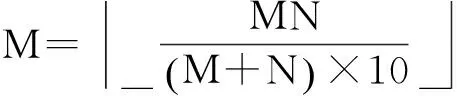
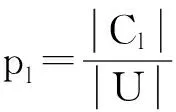
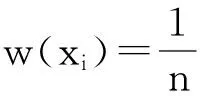
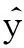

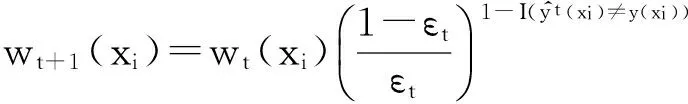
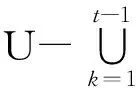
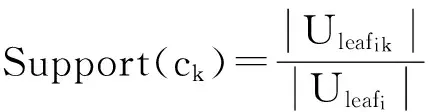
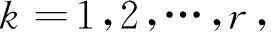
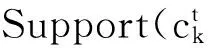
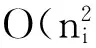
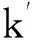
3 實驗結果及分析

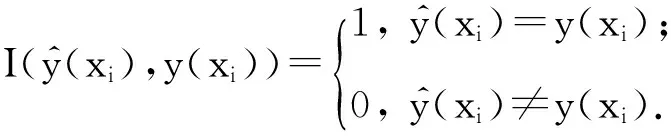
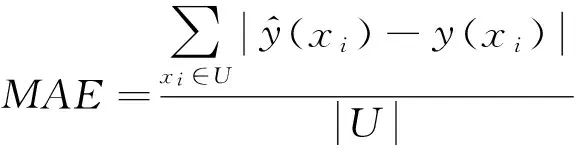
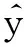

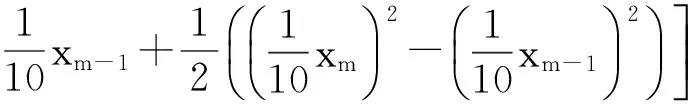
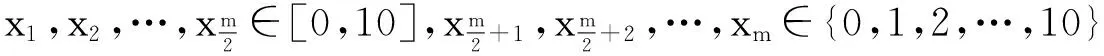
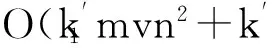
4 結束語




