薄壁球殼真空吸附裝夾變形力學分析與控制

何澤地，田東寧，楊金川，姚智慧

(1.中國工程物理研究院 材料研究所, 四川 綿陽 621700; 2.哈爾濱工業大學 機電工程學院, 黑龍江 哈爾濱 150001)

薄壁球殼真空吸附裝夾變形力學分析與控制

何澤地1，田東寧1，楊金川1，姚智慧2

(1.中國工程物理研究院 材料研究所, 四川 綿陽 621700; 2.哈爾濱工業大學 機電工程學院, 黑龍江 哈爾濱 150001)

針對標準鋁合金薄壁球殼零件的裝夾變形問題，建立球殼變形的數學理論模型以及有限元仿真模型，實現了薄壁球殼真空吸附裝夾狀態的理論分析與仿真優化。明確了真空負壓與裝夾位置對球殼變形的影響；基于球殼與吸具之間的裝夾位置關系，完成了吸具主要尺寸參數的優化設計。優化后吸具樣件的測量結果表明，通過控制真空負壓以及改變裝夾接觸位置，可以有效減小球殼的裝夾變形，進而提高其加工的尺寸精度。

機械制造工藝與設備； 薄壁球殼； 真空吸附； 裝夾變形； 有限元仿真

0 引言

薄壁球殼件特別是輕材料結構件，因其結構相對復雜、相對剛度較低和壁厚較小等特點，加工中需要使用特殊的工裝進行裝夾固定。而在實際加工中，不同的裝夾方式甚至裝夾過程會使薄壁球殼在加工前已經產生不同程度的變形，并影響裝夾約束狀態和加工模態。由此，薄壁球殼在機床上的裝夾狀態及其產生的整體或局部變形會影響工件的加工精度，也造成了不同程度的加工誤差[1-3]，從而影響炸藥武器在聚心爆轟作用下的等壓變形精度，并進一步影響炸藥爆轟性能。

關于薄壁球殼等弱剛性零部件加工裝夾的相關研究已有較多，各自針對的問題也不盡相同。其中，王運巧等[4]和劉胤等[5]以減小裝夾過程的彈性變形為目標，基于商業虛擬軟件開展了弱剛性結構件銑削加工的裝夾物理模型研究。李雙躍等[6]以及Menassa等[7]和Kashyap等[8]利用有限元虛擬建模技術實現了加工件裝夾優化并選擇最佳定位支撐位置，從而減小了裝夾變形。張磊等[9]和Kaya[10]通過不同方法研究不同裝夾方式和裝夾布局，明確了裝夾力以及裝夾位置對復雜薄壁件的影響。雖然現階段的研究成果較多，但針對薄壁半球殼的車削加工裝夾研究較少，并多以傳統機械夾緊力作為研究點。

當前基于機械裝夾的薄壁件加工變形主要從材料、工藝和夾具等角度進行控制或優化，且研究對象多為薄壁平面件。對于薄壁球殼，由于其傳統機械卡盤式夾具造成的宏觀變形較大，在某些特殊生產過程中一般采用真空吸盤式工裝對球殼類零部件進行裝夾。真空吸盤式工裝又分為弧面、錐面以及平面3種形式，在車削過程中弧面及平面貼合吸具的設計與加工成本太高，表面質量要求也較高，不適用批量式生產。

因此，有必要基于現行錐面吸具，針對薄壁球殼在車削加工中的夾緊力、裝夾位置以及裝夾變形等進行研究，結合材料力學與有限元仿真技術，給出錐面吸具的優化設計方法并進行效果對比。

1 薄壁球殼真空吸附力學狀態

1.1 球殼受力分析

根據理論力學和材料力學分析，薄壁半球殼經過與真空錐面吸具貼合(即由球殼外表面和吸具的內錐面實現接觸)會出現整體和局部形變。加工前，薄壁球殼與真空錐面吸具之間的吸附裝夾示意圖如圖1所示。

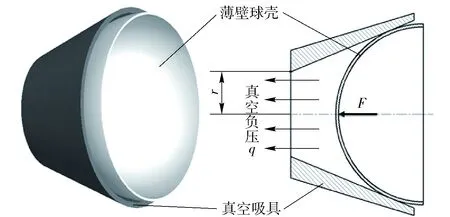
圖1 真空吸附裝夾示意圖Fig.1 Clamping state during vacuum suction

圖1中，q為真空負壓，即吸附狀態時的真空內外壓強差。由圖1可知，薄壁球殼與真空吸具裝夾后，吸具內錐面與球殼外弧面形成圓周線接觸，開啟真空負壓q后實現吸附裝夾。由于吸具錐面對球殼形成了線支承并產生支承力，同時球殼內表面受到空氣均布壓強，產生等效作用力F，從而使球殼產生裝夾變形。在考慮對稱的情況下，球殼受力狀態如圖2所示。

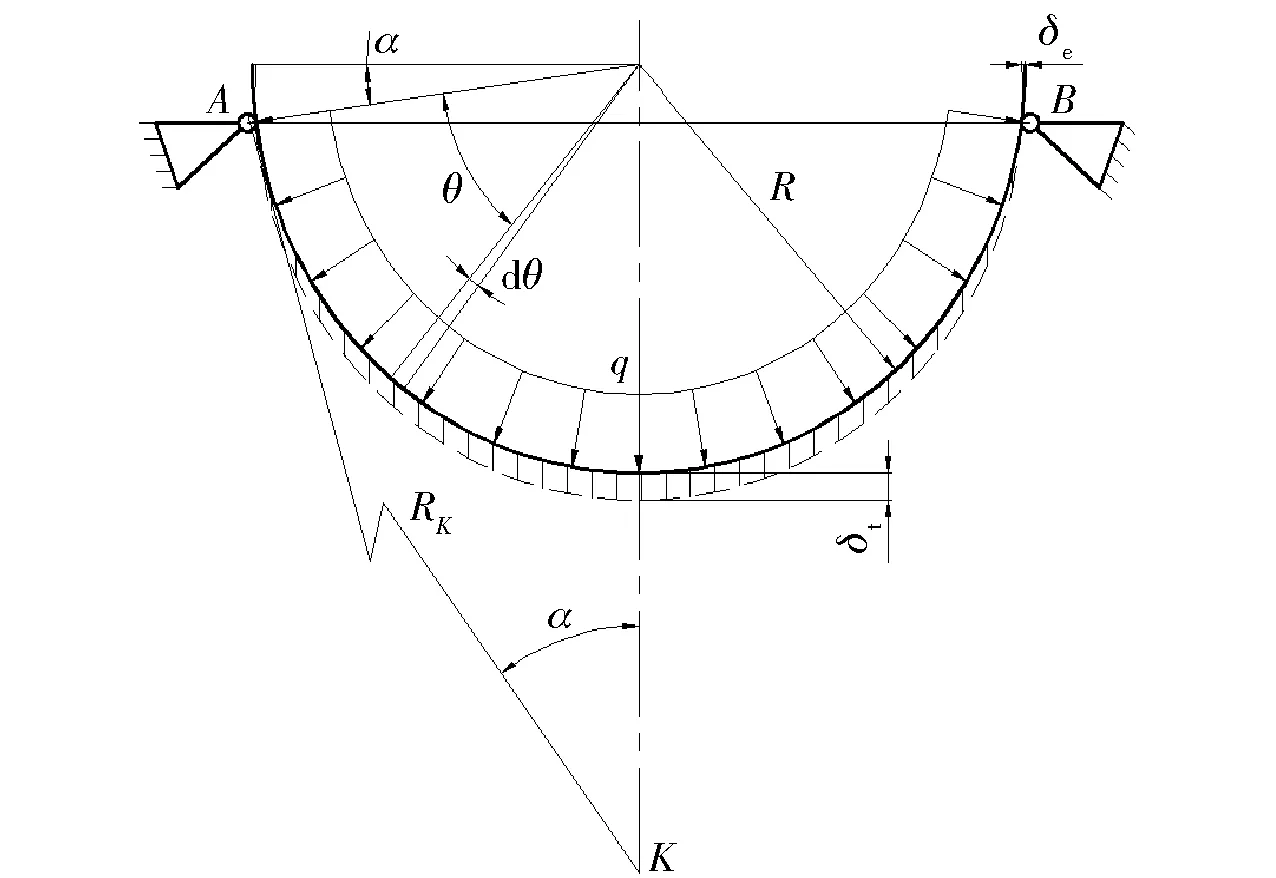
圖2 球殼應變及其應力分布狀態Fig.2 Strain and stress distribution states of spherical shell

圖2中：α為吸具錐面角度與端面到支承點- 圓心連線之間的角度相等；R為球殼表面半徑；θ為支承點- 圓心連線與計算點- 圓心連線之間的夾角；dθ為該微元段對應的弧度；δe為球殼端面變形量；δt為球殼頂部徑向變形量；RK為錐面吸具的錐心位置距支撐點的距離，K為吸具錐面的虛擬錐心；A、B為任意截面處球殼的支撐點。

可將正圓弧形薄壁球殼件等效為薄壁緩傾斜球殼殼體[11]。根據材料力學中的薄壁殼體計算與理論[12]，球殼微元段徑向受力狀態關系為

dp=qRdθsin (α+θ)2πRcos(α+θ).

(1)

由(1)式可得出，球殼整體徑向壓力為

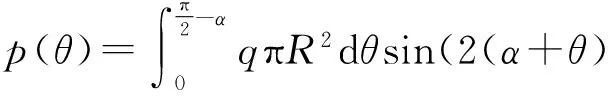
(2)

在空氣壓強作用并忽略球殼產生吸附滑移的情況下，球殼底部產生的徑向撓度為裝夾后的最大靜態變形位置，其變形量計算的一般形式為

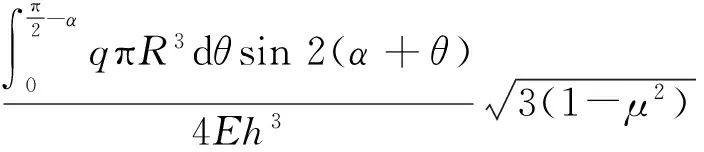
(3)

式中：E、h、μ分別為球殼材料的彈性模量、球殼殼體厚度、泊松比。

1.2 真空吸附力學模型

1.1節明確了薄壁球殼加工前的裝夾靜態力學狀態，而在實際裝夾過程中，還需要進一步考慮真空吸附和加工過程的可靠性與變形控制。

1)在吸具與工件形成的密封容積內，通過真空源抽出一定量的氣體、產生真空負壓q，進而吸具產生的等效吸附力[13]為

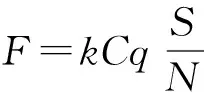
(4)

式中：k為真空有效吸附力系數，一般取值為0.9；C為換算系數，各參數單位為MPa、mm2、N時，取值為1；N為吸附時的安全系數，水平裝夾時N≥4，垂直裝夾時N≥8；S=nπr2k′為吸具的有效吸附作用面積，其中n為吸盤數量，r為吸具有效吸附半徑，即吸具的最小真空管徑，如圖1所示，k′為吸取力方向的投影面積系數，根據圖2所示幾何關系，其值通過(5)式確定：

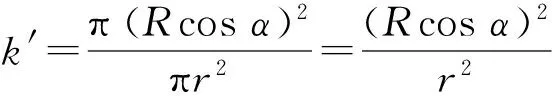
(5)

吸具有效吸附半徑r=25 mm，為恒定值。

根據(5)式，在薄壁球殼采用水平裝夾進行車削時，所需的真空吸附力為

(6)

根據(6)式，可得出在球殼重力和吸具結構確定的情況下，真空負壓的設定范圍為

(7)

由(7)式即可得出真空負壓q的范圍。在初設真空負壓q時，F可等效為球殼重力G.

2)在進行車削時，為保證球殼能被吸緊, 在車削加工中不會轉動滑移，必須使由球殼所受到的吸附力產生的與真空吸具之間的摩擦力Ff大于安全系數Q與切削力Ft的乘積，而摩擦力的大小與工件接觸支承力Fn有直接關系，球殼所獲得的支承力越大，則摩擦力越大。因此，球殼的切削力Ft與摩擦力Ff之間的關系為

Ff=ηFn≥QFt,

(8)

式中：η為鋁合金與鋼之間的摩擦系數，取值0.6；Fn為球殼總支承力，等效于工件接觸支承力；Q為安全系數，取值為2.

根據圖2和(2)式可得出，總支承力Fn與真空度之間的關系為

Fnsinα=p(θ).

(9)

已知6061鋁的車削力大小為

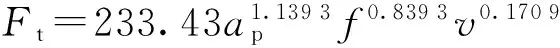
(10)

式中：ap為切削深度；f為進給量；v為切削速度。

將(2)式與(8)式、(9)式、(10)式聯立，可得出真空負壓q的預設下限值為

(11)

3)吸具內的真空負壓q應在真空發生器最大真空負壓的一定范圍內選擇，以提高真空吸著的能力，又不致使吸附的響應時間過長。而根據球殼加工過程中真空吸附系統的操作規程，真空負壓應在真空發生器最大真空負壓值的63%～95%范圍內選擇，即

q∈(0.63qmax，0.95qmax).

(12)

真空吸具在設計之初通常采用工件裝夾后的夾緊誤差，即裝夾變形量來表征或評價吸具的設計參數[14]。因此，由(11)式、(12)式、(7)式與(3)式聯立，并受到頂部變形量限值δl的控制，即可得出球殼真空吸附裝夾變形的數學優化模型：

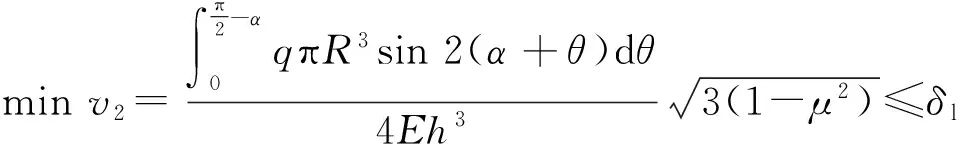
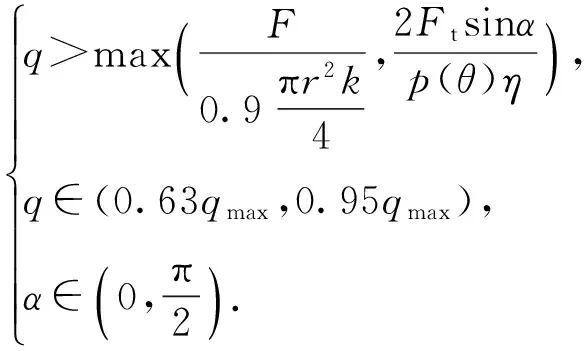
(13)

根據(13)式，吸具設計過程中的裝夾變形優化變量為錐面角度α，考慮加工穩定性的優化變量為真空負壓q.

通過(3)式、(6)式以及(9)式便可以表征薄壁球殼采用真空吸附裝夾的力學狀態，而(13)式則可作為優化真空錐面吸具及設定真空負壓的基礎理論與計算方法。

2 有限元仿真

根據薄壁球殼與真空吸具的裝配關系，本文采用有限元軟件ABAQUS來建立球殼真空吸附裝夾的仿真模型。薄壁球殼材料為6061鋁合金，其彈性模量及泊松比分別為E1=72 GPA和μ1=0.33；球殼尺寸為外徑R=60 mm，厚度h=1 mm，球殼質量G=1.71 N.

真空吸具材料為45號鋼，其彈性模量及泊松比分別為E2=210 GPA和μ2=0.3. 表面經過硬化處理，不考慮其錐面受力變形，可將其簡化為剛體。

以支撐接觸位置為界，整體有限元仿真模型在真空負壓作用下受力矢量q的狀態如圖3所示。

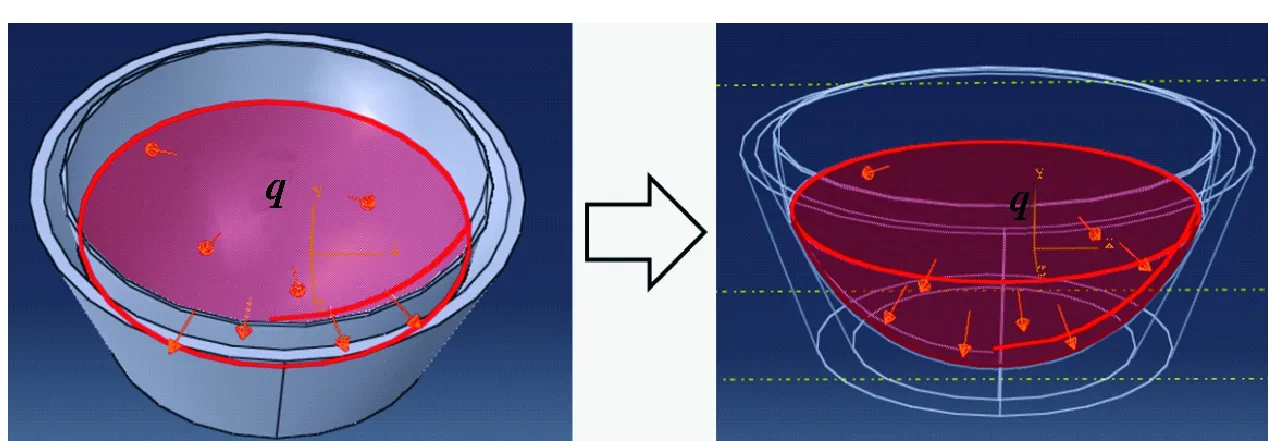
圖3 裝夾吸附受力狀態的有限元模型Fig.3 Finite element model of suction

圖3中，球殼與真空吸具分別采用C3D10(六面體)以及C3D8R(四面體)的三維應力實體單元。

2.1 仿真狀態分析

在裝夾過程中,由于裝夾布局參數的不同,薄壁件的裝夾變形程度也不同，裝夾布局參數引起的工件裝夾變形規律能夠通過有限元方法獲得[15]。

現將球殼的真空吸附接觸位置以球殼弧面坐標表示，如圖4所示。

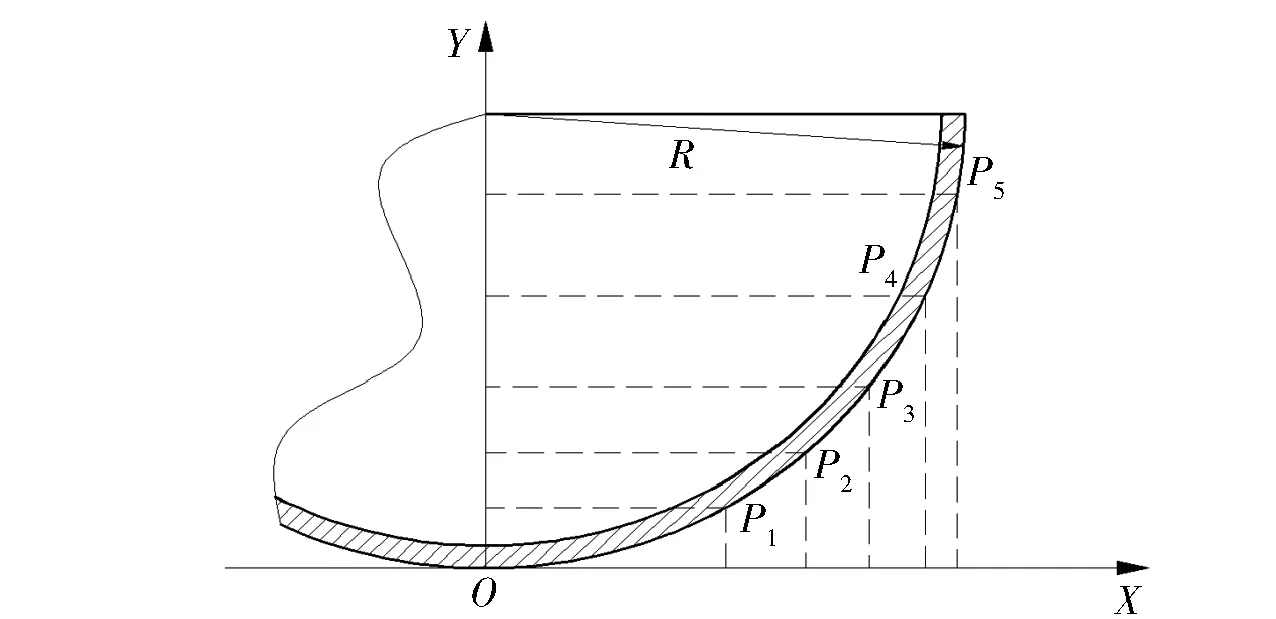
圖4 球殼吸附的不同接觸位置Fig.4 Contact positions of suction

根據吸附狀態下接觸的位置不同，吸具的錐面角度也存在差異，各位置坐標狀態如表1所示。

表1 吸附接觸位置的坐標數據

根據表1所示吸具的錐面角度，分別針對球殼建立吸具的仿真模型。已知現階段在球殼加工過程中設定的真空負壓q=0.001 MPa. 5個不同吸附接觸位置的仿真變形效果如圖5所示。

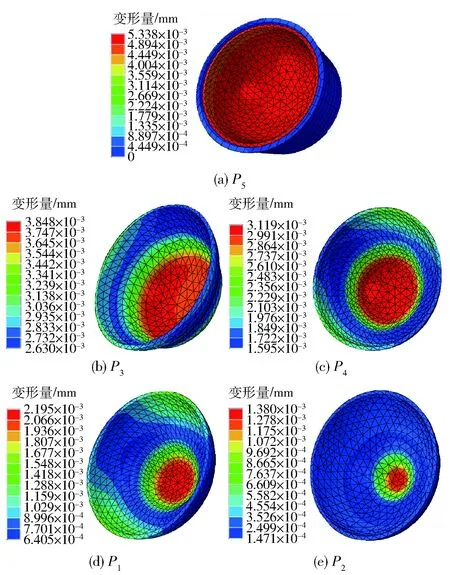
圖5 不同接觸狀態下底部變形量Fig.5 Deformation of shell in different contact states during suction

將球殼尺寸、材料數據以及真空負壓代入(3)式中，可得出在相同真空負壓下，吸具錐面角度與球殼裝夾變形量之間的關系，如圖6所示。

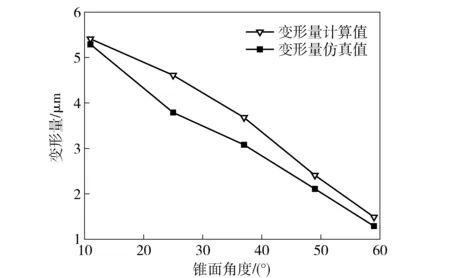
圖6 仿真后的變形趨勢Fig.6 Deformation trend after simulation

由圖6可知，裝夾變形程度與吸具錐面角度之間呈反比，即吸具錐面角度越大，球殼變形量越小。

2.2 真空負壓分析

圖6中的變化趨勢是在真空負壓保持一致的情況下得出的。因此，根據(5)式，當吸附同一球殼時，根據吸附位置的不同，穩定吸附時所需的真空負壓也存在差異。可以預知的是，錐面吸具角度越大，將球殼裝夾固定在吸具上所需的真空負壓最小值就越大，造成的球殼變形也就越大，從而對吸具系統提出了更高的要求。

根據(7)式理論模型、球殼狀態數據以及相同仿真路徑，可以得出在球殼不同吸附接觸位置進行裝夾時所需的最小真空負壓，如圖7所示。

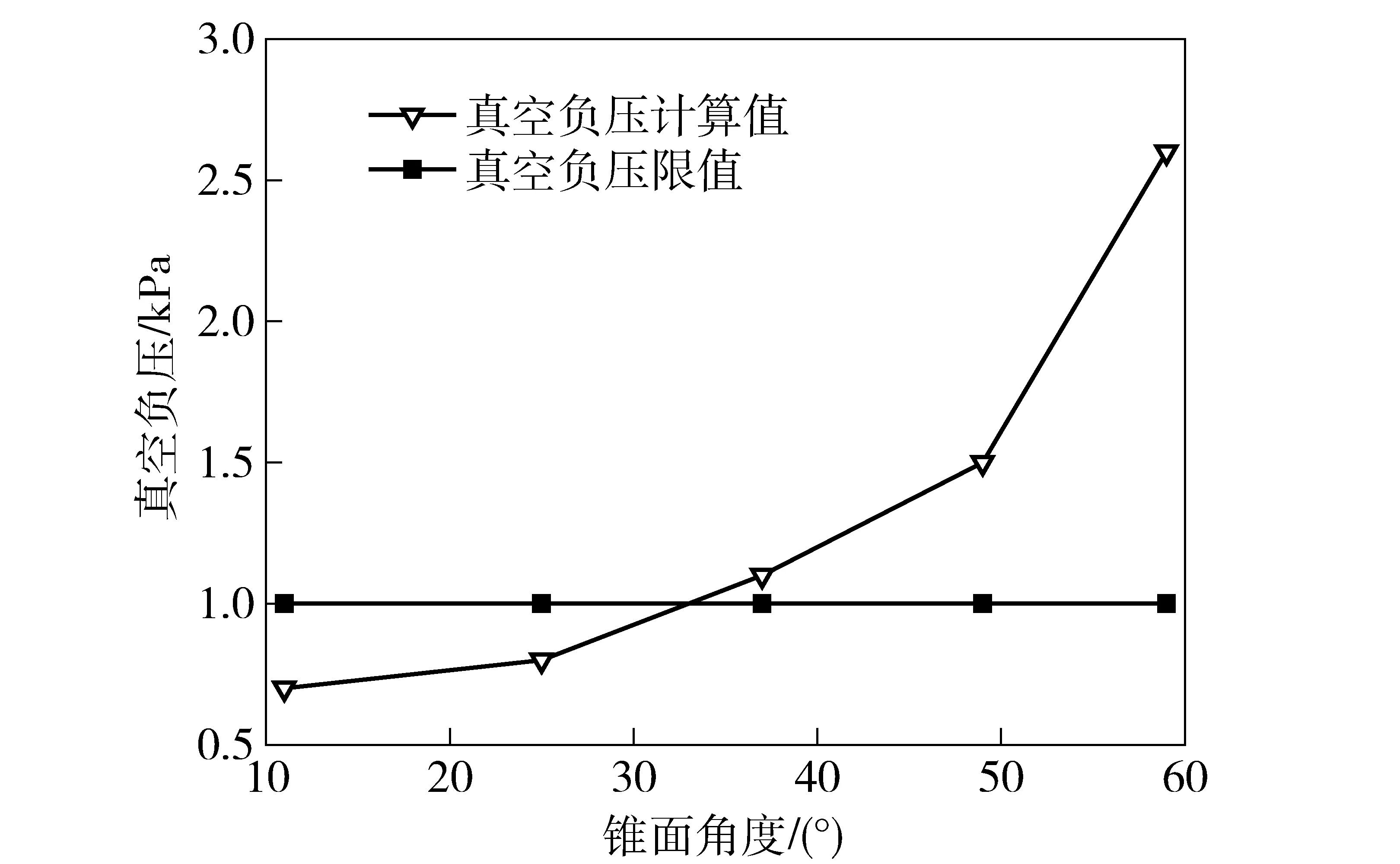
圖7 所需真空負壓變化趨勢圖Fig.7 Changing curves of different vacuum negative pressures

由圖7可知，錐面角度越大，所需最小吸附真空負壓越小。當錐面角度α>37°時，所需最小真空負壓已經明顯大于當前真空負壓限值(0.001 MPa)，在該真空負壓作用下的球殼在P1點處的變形量如圖8所示。

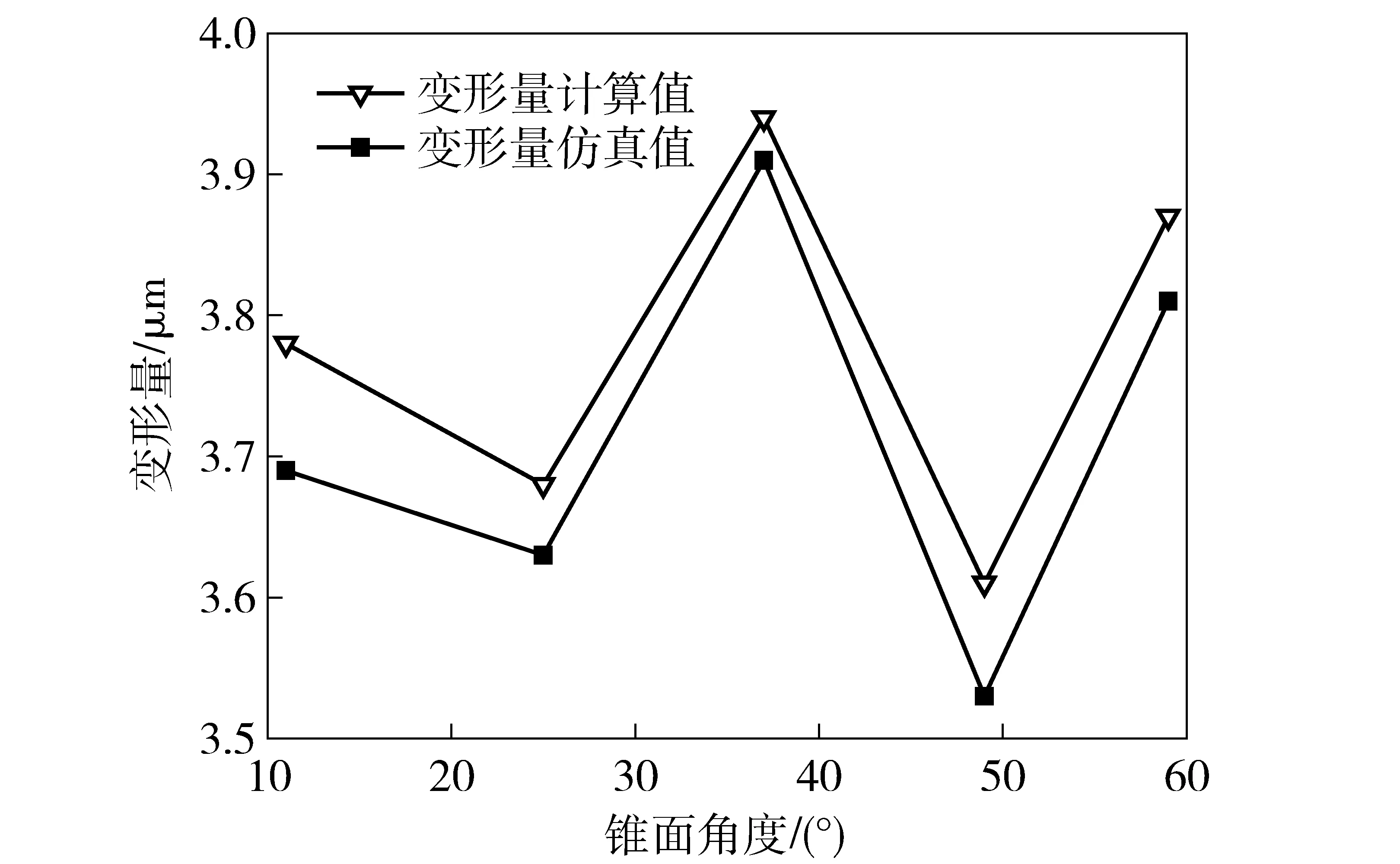
圖8 所需最小真空負壓狀態下的球殼變形趨勢Fig.8 Deformation trend of spherical shell under minimum vacuum negative pressure

結合圖6并由圖8可知，在設計真空吸具所需的最小真空負壓作用下，當錐面角度α>37°時，相對于圖6，對應球殼的裝夾變形量增大了。

3 優化分析與設計

根據前文分析，球殼變形及其幅度大小與真空吸具的錐面角度α以及真空負壓q有關。因此，根據(13)式可以對真空吸具進行優化設計。

優化前，需要明確設計輸入條件如下：

1)待加工的薄壁球殼尺寸狀態；

2)車削加工相關參數；

3)現有真空負壓可用范圍。

已知球殼材料為6061鋁合金，球殼外徑R=60 mm，厚度h=1 mm；鋁合金與鋼之間的摩擦系數η=0.6. 切削參數為：切削深度ap=0.3 mm；進給量f=0.1 min/r；切削速度v=100 m/min；真空吸附口半徑r=25 mm；真空負壓最大值qmax=0.001 0 MPa.

加工前，根據加工技術要求，球殼在真空吸附狀態下產生的裝夾變形量需控制在δl≤3 μm，則(13)式所建立的數學優化模型變形為

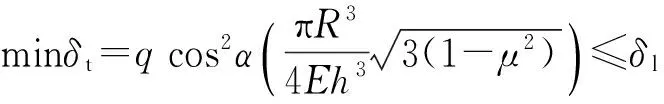
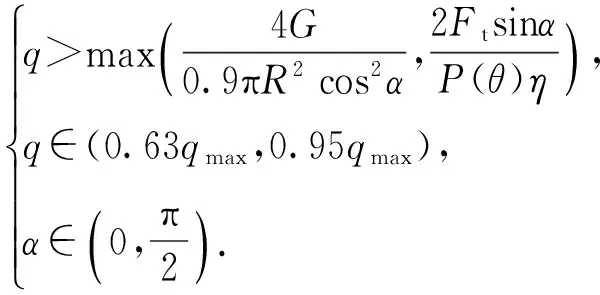
(14)

由(14)式得出的吸具錐面角度優化選擇范圍為

α∈(17.4°,29.6°).

(15)

將所屬各參變量代入(14)式中，得出球殼真空吸附裝夾的真空負壓與錐面角度的優化結果為

(16)

根據上述優化結果，得出的吸附變形理論計算值為δt=2.31 μm，符合吸附裝夾的變形控制要求。仿真結果和吸具樣件(α=26.5°)如圖9所示。

圖9的仿真數據顯示，吸附變形的仿真值為2.17 μm，吸附后所產生的裝夾變形量減小了。

采用瑞典Serein公司產croma564改進型三坐標測量儀進行測量，其標準系統測量分辨率為0.05～0.07 μm，測量精度為0.5 μm. 此外，設計一個適用于工裝與真空吸附系統的小型大理石平臺，中間開孔以方便測量時的真空管路連接，先采用0.003 MPa進行球殼的初始固定，然后在精度為0.1 μm的端面激光位移傳感器測量下進行裝夾與端面對中，使其端面跳動控制在0.5 μm以下。

采用同平面垂直對稱4點法，分別對經過優化后吸具樣件和原36°錐面吸具裝夾后的球殼內表面進行檢測。分別在P1～P5所處的平面內(如圖10中P1所處的同平面垂直4點P11～P14)檢測，并與裝夾前的球殼對應位置進行數據對比，采用測量點的內深變化量作為標定，從而得出裝夾變形量。

經過檢測后，原36°錐面吸具在0.007 5 MPa真空負壓作用下，對比裝夾前后的球殼測量數據，得出球殼的裝夾變形量如表2所示。

經過檢測后，優化后的吸具樣件在0.007 5 MPa真空負壓作用下，對比裝夾前后的球殼測量數據，得出球殼的裝夾變形量如表3所示。

由表2與表3的實際測量數據對比分析可知，優化后的吸具樣件在球殼裝夾后，球殼的變形量為1.60～2.80 μm，較原36°吸具的變形量大幅減小，整體變形控制效果明顯。其中，25°位置由于接近球殼與吸具的接觸點，其變形量最小；11°位置受到球殼整體變形影響，其變形程度較球殼底部小；球殼底部由于相對遠離吸附支撐點，其變形也最大。

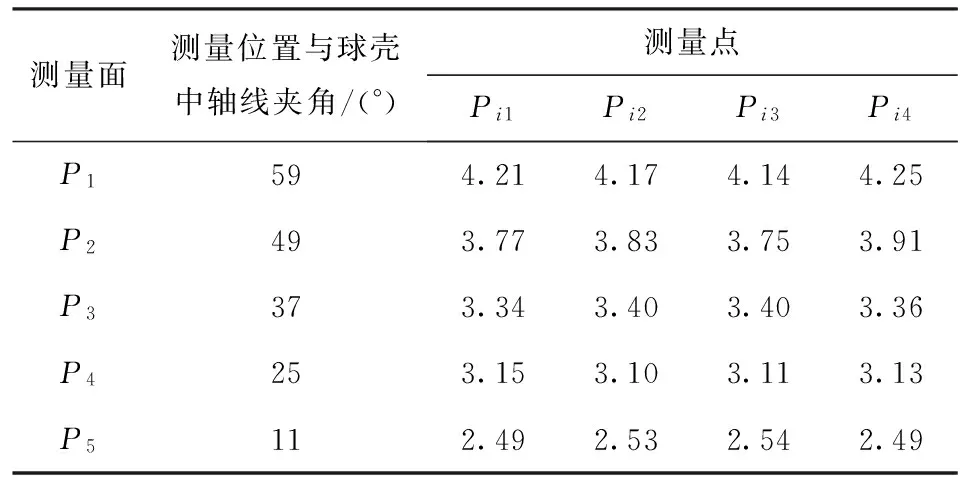
表2 原36°錐面吸具裝夾前后的變形量

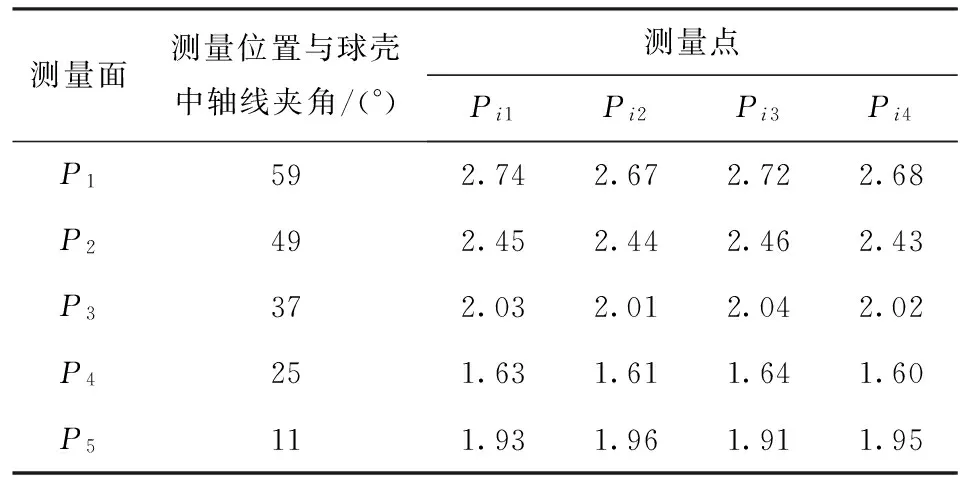
表3 26.5°錐面吸具裝夾前后的變形量

綜上所述，考慮到實際吸附裝夾中存在一定的滑移以及測量誤差，可以認為本文真空吸具的結構優化設計是合理有效的。

4 結論

通過理論分析和實例計算，得到如下結論：

1)吸具錐面角度與真空負壓影響薄壁球殼真空吸附狀態下的裝夾變形。

2)基于該薄壁球殼真空吸附的力學狀態等效數學模型及變形控制，可以較精確地得出吸具錐面角度的優化選擇范圍。

3)優化后的實例計算、仿真分析以及樣件測量數據表明，通過優化真空負壓及裝夾接觸位置，可以有效地減小薄壁半球殼產生的裝夾變形，進而提高加工尺寸精度。

References)

[1] 秦國華，吳竹溪，張衛紅．薄壁件的裝夾變形機理分析與控制技術[J]. 機械工程學報，2007，43(4)：211-216． QIN Guo-hua,WU Zhu-xi,ZHANG Wei-hong. Analysis and control technique of fixturing deformation mechanism of thin walled workpiece[J]. Chinese Journal of Mechanical Engineering, 2007,43(4):211-216.(in Chinese)

[2] 王軍，耿世民，張遼遠，等．薄壁殼體件裝夾變形機理有限元分析與控制[J]. 兵工學報，2011，32(8)：1008-1013． WANG Jun,GENG Shi-min,ZHANG Liao-yuan,et al. Finite element analysis and control of clamping deformation mechanism of thin-wall shell workpiece[J]. Acta Armamentarii, 2011, 32(8):1008-1013.(in Chinese)

[3] 李暉，張林林，常永樂，等．約束層阻尼對薄壁圓柱殼模態參數的影響研究[J].兵工學報，2016，37(7)：1338-1344. LI Hui, ZHANG Lin-lin, CHANG Yong-le, et al. The influence of constrained layer damping on modal parameters of thin cylindrical shell[J].Acta Armamentarii, 2016,37(7):1338-1344.(in Chinese)

[4] 王運巧，梅中義，范玉青．薄壁弧形件裝夾布局有限元優化[J]. 機械工程學報，2005，41(6)：214-217． WANG Yun-qiao, MEI Zhong-yi, FAN Yu-qing. Finite element optimization of mechining fixture layout of thin-walled arc workpiece[J]. Chinese Journal of Mechanical Engineering,2005,41(6):214-217.(in Chinese)

[5] 劉胤，胡小秋．基于ABAQUS的弱剛度結構件裝夾布局優化技術[J]. 工具技術，2008，42(11)：19-22． LIU Yin, HU Xiao-qiu. Optimum technology on clamping distribution of low-rigidity structure part based on ABAQUS[J]. Tool Engineering,2008,42(11):19-22. (in Chinese)

[6] 李雙躍，劉建波．自動裝夾設計中支承位置與工件變形的幾何推理方法[J]. 組合機床與自動化加工技術，2003，58(8)：16-19． LI Shuang-yue,LIU Jian-bo. Geometric reasoning approach for supporting position and workpiece deformation in the automation fixturing design[J]. Modular Machine Tool & Automatic Manufacturing Technique,2003,58(8):16-19. (in Chinese)

[7] Menassa R J, Devries W R. Opimization methods applied to selecting support positions in fixture design[J].Journal of Manufacturing Science & Engineering,1991, 113(4):412-418.

[8] Kashyap S, Devries W R. Finite element analysis and optimization in fixture design[J]. Structual Optimization, 1999,18(2/3): 193-201.

[9] 張磊，陳克勤，張大順，等．復雜薄壁件裝夾變形控制研究[J]. 長春理工大學學報，2014，37(4)：89-92． ZHANG Lei,CHEN Ke-qin,ZHANG Da-shun,et al. Research on fixture deformation of the complex aluminum thin-walled parts[J].Journal of Changchun University of Science and Technology,2014,37(4):89-92.(in Chinese)

[10] Kaya N. Machining fixture locating and clamping position optimization using genetic algorithms[J]. Computers in Industry, 2006, 57(2):112-120.

[11] 章毅，陳力，李杰，等．薄壁殼在外部承受沖擊荷載作用下的動力響應分析[J].工業建筑，2010，40(4)：46-50. ZHANG Yi,CHEN Li,LI Jie,et al.Analyses of the dynamic responses of the thin-walled shell under external impact[J]. Industrial Construction,2010,40(4):46-50.(in Chinese)

[12] 吉布森 J E．薄殼計算與理論[M]．北京：國防工業出版社，1989：101-109． Gibson J E. Thin shells computing and theory[M]. Beijing:National Defense Industry Press,1989:101-109.(in Chinese)

[13] 單景德．真空吸取器設計及應用技術[M].北京：國防工業出版社，2000：56-61． SHAN Jing-de. Design and application technology of vacuum absorption device[M]. Beijing:National Defense Industry Press,2000:56-61. (in Chinese)

[14] 蔡成，馬術文，楊欣雨，等．裝夾方案評價技術研究[J]. 機械設計與制造，2016，308(10)：207-029． CAI Cheng,MA Shu-wen,YANG Xin-yu,et al.Study on the evaluation technology of clamping scheme[J].Machinery Design & Manufacture,2016，308(10)：207-209.(in Chinese)

[15] 秦國華，趙旭亮，吳竹溪．基于神經網絡與遺傳算法的薄壁件多重裝夾布局優化[J]. 機械工程學報，2015，51(1)：204-210． QIN Guo-hua,ZHAO Xu-liang,WU Zhu-xi.Optimization of multi-fixturing layout for thin-walled workpiece based on neural network and genetic algorithm[J]. Journal of Mechanical Engineering,2015，51(1)：204-210.(in Chinese)

Control and Mechanical Analysis of Clamping Deformation of Thin-walled Spherical Shell Workpiece during Vacuum Suction

HE Ze-di1， TIAN Dong-ning1， YANG Jin-chuan1， YAO Zhi-hui2

(1.Institute of Materials, China Academy of Engineering Physics, Mianyang 621700, Sichuan, China; 2.School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, Heilongjiang, China)

The thin-walled spherical shell workpiece is liable to deform during clamping before machining. A standard aluminum-alloy shell is taken for example. A mathematical model is established based on spherical deformation mechanism and finite element analysis. The theoretical analysis and simulation optimization are carried out for clamping design of semi-spherical shell with vacuum suction. The influences of suction strength and clamping location on deformation in the state of air pressure under average distributed load are analyzed. The result shows that the clamping deformation of shell can be minished effectively by controlling the suction strength and modifying the clamping location so that the machining size accuracy is improved. The main design parameter of vacuum fixture is optimized for the location relationship between shell and fixture.

manufaturing technology and equipment; thin-walled spherical shell; vacuum suction; clamping deformation; simulation

2016-11-27

裝備“十二五”預先研究項目(42601070202)

何澤地(1963—), 男, 工程師。E-mail: hezedi@caep.cn

楊金川(1988—), 男,工程師。E-mail: yangjinchuan@caep.cn

TG751.1

A

1000-1093(2017)07-1409-07

10.3969/j.issn.1000-1093.2017.07.020