淺談如何上好數學復習課
常娟
摘 要:單元復習課是對章節學習的總結,它不僅要求章節中的所有知識點都能聯系起來,構成完整的知識體系,而且要求以學生為本,在學生通過合作交流解決問題的過程中,不斷滲透重要的數學思想方法。中國著名的教育家孔子曾提出“學而時習之”“溫故而知新”的主張,說明通過復習已學的知識,可以提升理解能力,也可以獲得新的領悟,這正是復習課的重要性。
關鍵詞:數學;復習課;軸對稱圖形
學生是課堂教學的主體,而學生往往認為新授課新鮮有趣,而復習課枯燥無味。面對這種情況,教師不僅要在思想上提高學生對復習課重要性的認識,而且要以“新風景”來提高學生的積極性。“新授課育樹,復習課育林”,一節好的單元復習課,不僅要使學生鞏固已學知識,查漏補缺,彌補新授課解決不了的問題,還要繼續深化得到新知,在交流討論解決問題的過程中,不斷提升學生的數學思維品質。下面,筆者以義務教育教科書數學(蘇科版)八年級上冊第2章《軸對稱圖形》單元復習課為例,淺談怎樣上好一節單元復習課。
一、注意基本概念的比較
筆者首先請學生回顧軸對稱及軸對稱圖形的概念,以兩幅圖為例,通過定義和圖像結合分別說出它們的異同點。通過概念,拋磚引玉,學生可進一步鞏固線段、角、等腰三角形以及等邊三角形和等腰直角三角形的軸對稱性。
二、注意性質、定理的運用
教育家陶行知先生提倡“行是知之始,知是行之成”,即是說學生的能力并不是靠“聽”得到,而是靠“做”得到的,只有動手操作才能出真知。為了使學生更透徹地理解軸對稱圖形中的線段和角的性質、定理的“逆向”思考,筆者通過實際生活問題引入,不僅提高了學生的作圖能力,而且使學生對文字的理解也能體現在畫圖中,從而提高了學生運用知識解決實際問題的能力,發展了學生的思維能力,讓他們感受復習課的魅力。
練習1:到三角形的三個頂點距離相等的點是( )
A.三條角平分線的交點 B.三條中線的交點
C.三條高的交點 D.三條邊的垂直平分線的交點
練習2:到三角形的三邊距離相等的點是( )
A.三條角平分線的交點 B.三條中線的交點
C.三條高的交點 D.三條邊的垂直平分線的交點
三、講練結合,探索一題多解、一題多變
復習課精講精練,這是從教學實踐中總結出來的好方法。學生做練習并不一定要老師領著,筆者提倡學生自主、討論、合作完成練習。練習過程中教師要幫助學生理清題目所包含的知識點,指出常見的錯誤、應該主意的問題、題目有幾種解法,并根據題目進行變式訓練,從而體現復習課與新授課的不同之處,它是教與學的過程中必不可少的環節。《軸對稱圖形》復習課中筆者給出了下面一道例題,讓學生自主練習。
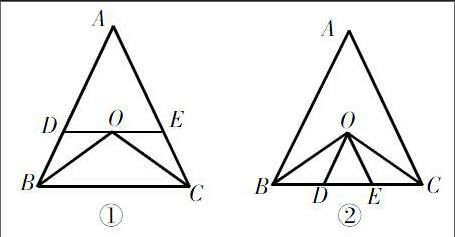
例1:如圖,在△ABC中,BO平分∠ABC,CO平分∠ACB,過點O作DE∥BC,交AB于點D,交AC于點E.
(1)試找出圖①中的等腰三角形,并說明理由。
(2)圖①中,若AB=12,AC=11,求△ADE的周長。
(3)若將原題中平行線DE的方向改變,如圖②,OD∥AB,OE∥AC,點D、E在邊BC上,BC=16,△ODE的周長是多少?
四、注意數學思想的滲透
數學思想與方法是數學學習的精髓,是聯系數學中各類知識的紐帶。初中數學中常用的數學思想有:化歸思想、數形結合思想、方程思想、分類討論思想、類比與歸納思想以及數學建模思想等。筆者結合本章節情況,兩次滲透分類討論思想。
練習3:△ABC為等腰三角形,若∠A=40°,則∠B= 。
練習4:等腰三角形一腰上的高與另一腰的夾角為40°,則該等腰三角形的底角度數為 。
上述兩道練習中,練習3是分類討論∠A是等腰三角形中的頂角還是底角,練習4是分類討論等腰三角形的高是落在了內部還是外部。它們是對等腰三角形角、邊、高的特殊性的分類討論,是一類重要題型,筆者將這兩道題目放在一塊討論,能使學生更系統地了解等腰三角形的性質,同時加強學生思維能力的訓練。
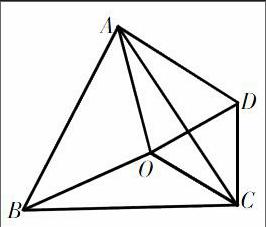
例2:如圖,O為等邊三角形ABC內一點,∠AOB=110°,∠BOC=α,將△BOC繞著C點旋轉成△ADC,連接OD。
求證:(1)△COD是等邊三角形。
(2)∠ADO= °,∠AOD= °。(用含有α的式子表示)
(3)探究:當α為多少度時,△AOD是等腰三角形?
例2考查了旋轉的性質、等腰三角形的性質以及等邊三角形的性質,巧妙地融合了本章節內容,由淺入深,層層遞進,包含了運動變化、數形結合、分類討論、方程思想等,能較好地考查學生的推理、探究及解決問題的能力,使得學生能力有所提升。
總之,復習課的任務很艱巨,需要教師精心準備,做到心中有數,使得內容“全”、習題“精”、方法“活”、時間“足”,力求對所學的基礎知識從具體到抽象,從局部到整體等多層次、多角度、全方位地融會貫通。復習課應該不拘泥于形式,也可以把知識系統化,通過知識列表或畫出知識結構圖進行,讓學生感受它與新授課不同的風景,只有正確進行學法指導,精心設計問題,才能使學生處于教學的主體,同時有意識地培養學生的分析理解能力、綜合概括能力和抽象思維能力。
參考文獻:
尤永銀.淺談如何上好初中數學復習課[J].新課程研究,2012(3).
編輯 任 壯

