關于雙曲線若干問題的探討

楊德甘肅省卓尼縣柳林中學

關于雙曲線若干問題的探討

楊德
甘肅省卓尼縣柳林中學

雙曲線是圓錐曲線的重要內容之一，也是高考的熱點問題，知識綜合程度較高，且易于發散，運算復雜．此中不乏雙曲線的第二定義和焦點弦等問題，無疑，這類問題在啟迪學生思維，拓寬解題思路等諸多方面都有十分重要的作用，因而它在中學數學教材及各種復習資料中始終占有一席之地，針對雙曲線的第二定義、焦點弦等問題及其應用，有必要作進一步的探討和研究。

新課改；雙曲線；焦點弦；第二定義

1 引言

新的數學課程標準是在以學生發展為本的理念下，要求學生轉變學習方式，教師積極探索，轉變教與學觀念，加深對課本內容的拓展理解和應用。所以，在數學教學中，教師應善于引領學生對課本的一些重要問題進行進一步的探索與研究，以提高學生的數學素質與應試能力。

2 雙曲線的兩個定義

定義1我們把平面內與兩個定點F1，F2的距離的差的絕對值等于常數（小于F1F2）的點的軌跡叫做雙曲線．這兩個定點叫做雙曲線的焦點，兩焦點間的距離叫做雙曲線的焦距。

定義2平面上與一個定點（焦點F）的距離和一條定直線（準線l）的距離的比等于常數e的點的軌跡，當0＜e＜1時是橢圓;當e＞1時是雙曲線;當e=1時是拋物線。()

例1已知點P到定點F2c,0的距離和它到定直線l∶x=的距離比是常數(c＞a＞0)，求點P的軌跡。

解設P(x,y)根據題意得：

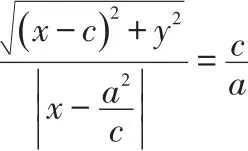
化簡得

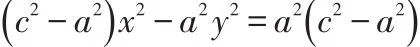
令c2-a2=b2，則上式可化為

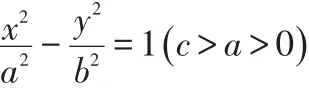
由此得雙曲線的標準方程，這個雙曲線的離心率就是P到定點F2的距離和它到定直線l（F2不在l上）的距離比。

事實上，在由第一定義推導雙曲線標準方程時，曾得到這樣一個式子：

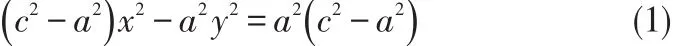
令c2-a2=b2，則上式可化為：

如果對(1)式做如下處理

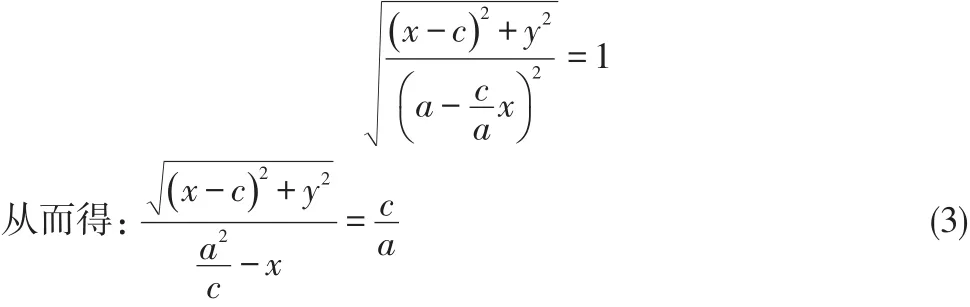
(3)式的幾何意義是∶

動點Px,y到定點Fc,0的距離與P到定直線l∶x=的距離的比值是一個常數=e＞1(c＞a＞0)．這正好是雙曲線的第二定義，由此可見雙曲線的第一、二定義是相互包容的。

3 焦點弦問題

定義3經過圓錐曲線焦點且被圓錐曲線截得的線段叫做焦點弦。

這是一個非常重要的幾何量，在歷次考試中出現頻率較大，且形式多樣。

過雙曲線焦點F且與該雙曲線交于A，B兩點，傾斜角為α，則有

(1)當直線l與雙曲線的兩個交點A，B在雙曲線的同支上時，

(2)當直線l與雙曲線的兩個交點A，B在雙曲線的異支上時，

(3)當直線l與雙曲線只有一個交點時，

證明由對稱性，不妨設F為有焦點(c,0)

(1)由漸近線與弦AB斜率的關系知

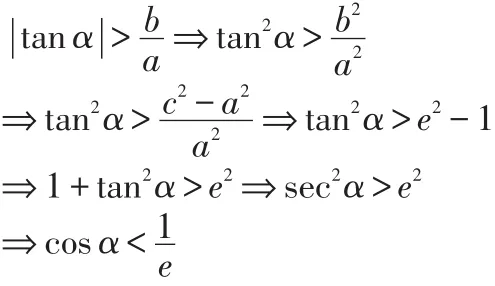
(2)首先A，B在雙曲異支上時，由漸近線與弦AB斜率的關系知

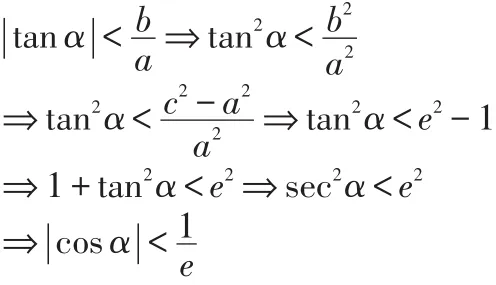
(3)由于直線l與雙曲線有且只有一個交點，依題意則直線l與該雙曲線的漸近線平行，即

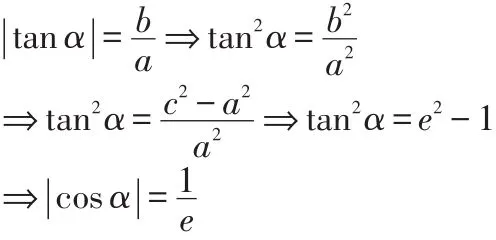
對焦點在y軸上的雙曲線而言，也有上述性質。

[1]陳炆.圓錐曲線統一定義與統一方程中若干問題釋疑[J].數學通訊，2010(12)∶10-12.

[2]巨鵬，孫月芳.圓錐曲線焦點弦長的公式求法[J].內江科技，2010(5)∶31-32.

[3]彭世金.圓錐曲線焦點弦長的一個公式及應用[J].數學通訊，2007(22)∶22-23.

楊德，中學一級教師，現任甘肅省卓尼縣柳林中學政教處主任。