一題多變拓展思維

寧安市石巖學校 金同雙

一題多變拓展思維

寧安市石巖學校 金同雙

在教學過程中運用“一題多變”的教學手段，能有效培養和拓展學生思維，有利于提高教學效果，對提高學生分析問題、解決問題的能力也有很好的作用.

一題多變是題目結構的變式，是指變換題目的條件或結論，變換題目的形式，或者將某項條件與結論交換等，而題目所考查的實質不變，變化的目的是從不同角度、不同方面揭示題目的本質.用這種方式進行教學，可以促使學生根據變化的情況積極思索，設法想出解決問題的辦法，從變中總結解題方法，從變中發現規律，從變中發現“不變”，從而培養思維的靈活性.

“一題多變”的常用變換方法有：1.變換命題的條件與結論；2.保留條件，深化結論；3.探討命題的推廣；4.生根延枝，圖形變換；5.接力賽，一變再變；等等.

現以人教版《數學》九年級下冊第二十七章“相似”中的“相似三角形”課后第13題為例，列舉從簡到難的10個變式并適度剖析.

原題：已知，在△ABC中，CD是邊AB上的高，且AD:CD=CD:BD，求：∠ACB的大小.

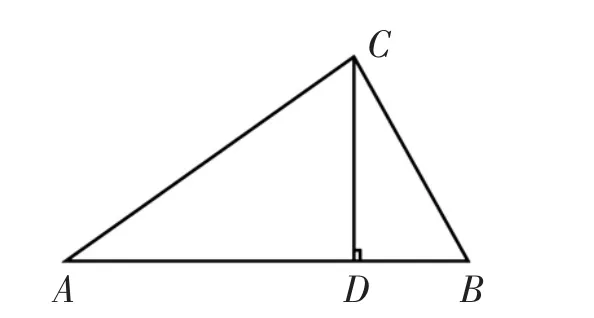
題型變式：

1.圖中和∠CAB相等的角有哪些？和∠CAB互余的角有哪些？

2.求證：AC·BC=AB·CD.

3.求證：S△ADC:S△CDB=AD:DB.

4.求證：AC2=AD·AB；BC2=BD·AB.

5.（變換命題的條件與結論）（1）如果AC=2BC，那么5CD=2AB；（2）求證

6.（其他條件不變，增加原題的條件）AE平分∠BAC交BC于點E，求證：CE:EB=CD:BC.

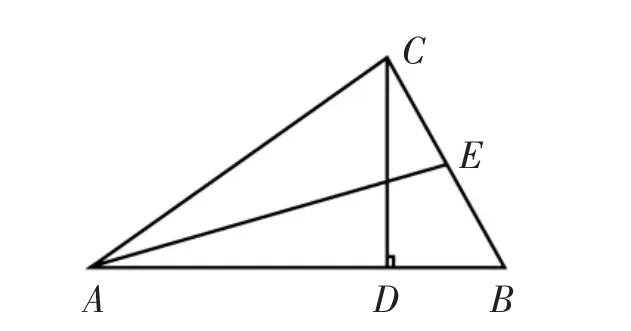
7.（在第6題中增加點F，結論改變）已知，在△ABC中，CD是邊AB上的高，且AD:CD=CD:BD，AE平分∠BAC交BC于點E，交CD于F，求證：2CF·FD=AF·EF.

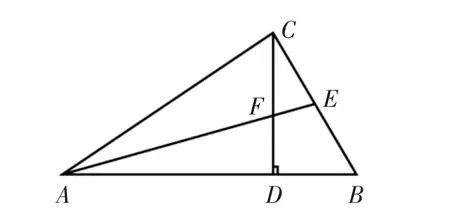
8.（在原題中增加2個條件，改換結論）已知，在△ABC中，CD是邊AB上的高，且AD:CD=CD:BD，DE⊥AC于E，DF⊥BC于F，求證：（1）CE:BC=CF:AC；（2）CD3=CE· CF·AB.

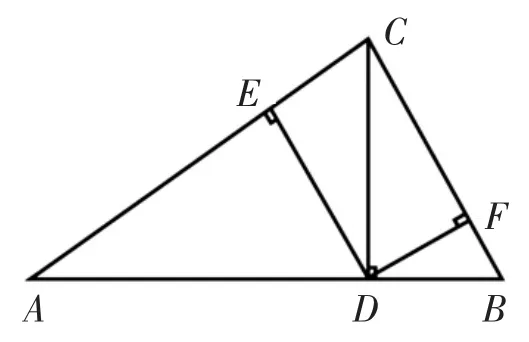
9.（接力賽，一變再變，擴大知識的延伸）已知:在△ABC中，CD是邊AB上的高，且AD:CD=CD:BD，以CD為直徑的圓交AC、BC于E、F，求證：CE:BC=CF:AC.

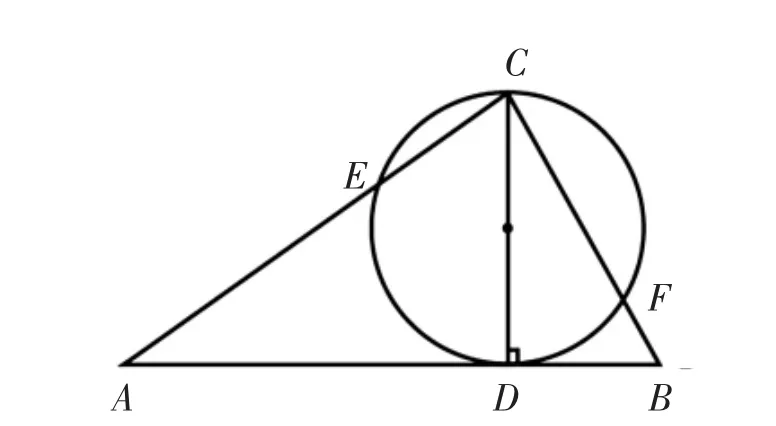
10.（生根延枝，圖形變換）已知:在△ABC中，CD是邊AB上的高，且AD:CD=CD:BD，延長CB到E，使EB=CB，連結AE、DE，求證：DE·AB=AE·BE.

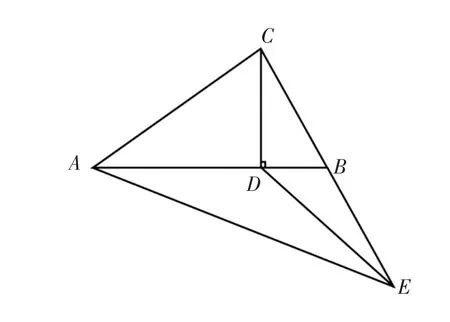
本套變式題展示的主題和創編意圖是：利用對應邊成比例，用兩個直角三角形相似性質證明結論.為了考查學生在開放條件下還能猜想到哪些可能出現的結論，我在這一組變式題的設計中充分考慮到了這些相關考點.另外，結合《課程標準》的要求：學生要了解相似三角形的判定定理；了解相似三角形的性質定理；了解三角形與各種幾何圖形之間的密切聯系.我設計了幾種變式來鞏固“相似三角形”的相關知識.

第1題：在保持原題條件不變的基礎上認識圖形，相似圖形與哪些角有重要關系.

第2、3、4題：保留原題條件，改變結論.從不同角度考查學生對相似三角形的判定定理、性質定理和比例性質的理解，對三角形面積公式之間的聯系的掌握情況，以及證明結論的能力.

第5題：變換命題的條件與結論.

第6、7題：在原題基礎上增加條件，如中點、角平分線及垂線等題設條件，利用角的等量代換和直角三角形兩銳角互余的關系得出兩三角形相似，考查了學生對三角形相似的判定的掌握情況，在不同的條件下采取不同的判定方法.此題考點較多，但難度適中，適合學生練習.

第8題：探討命題的推廣，在變式7的基礎上增加兩條垂線，圖形看似復雜了，結論也改變了，但是，難度并沒有增加.命題得到了進一步推廣，但考點沒變.

第9題：此變式主要體現相似三角形與圓的知識的連接.條件、結論一變再變，擴大了知識的延伸.通過同弧圓周角相等知識解決兩三角形相似，考查范圍擴大，考查了學生的知識綜合應用能力以及變通能力.

第10題：生根延枝、圖形變換，在改變原題條件的基礎上再次變換結論，難度沒有增加，考點不變.

教師在運用“一題多變”教學手段時要注意，無論題目怎樣變化，考查范圍必須遵從《課程標準》的要求，不得超越學生的認知水平，否則變式就是無意義的.一題多變的意義在于啟迪思維，開闊視野，提高學生思維敏捷性、靈活性和深刻性.有利于學生發散思維能力的培養和解題技巧的提高；有利于將知識、能力和思想方法在更多的新情景、更高的層次中反復滲透，從而實現螺旋式的再認識、再深化；有利于有效提高課堂教學質量和學生綜合素質.

通過“一題多變”的教學實踐和探究，我的課堂教學效率和教學質量都有所提高，教學專業水平也得到了提升，同時，學生的思維開闊了，課堂氣氛活躍了，學生的學習興趣提高了，對知識的理解和掌握加深了，成績也普遍提高了.現在，我的學生已經養成了這樣的習慣：每當聽老師講一道例題或自己做一道習題時，都要嘗試改變條件和結論再試一試.這種學習習慣和學習方式無形之中調動了學生的學習積極性，激發了學生的創新意識，同時也起到了舉一反三、事半功倍的效果.

編輯/王一鳴E-mail：51213148@qq.com