穿孔消聲器聲學計算的快速多極混體邊界元法

楊亮，季振林

(哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001)

穿孔消聲器聲學計算的快速多極混體邊界元法

楊亮，季振林

(哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001)

為提高計算效率以及擴展計算頻率范圍，本文將混體邊界元方法與快速多極算法結合用于穿孔消聲器的聲學性能計算。通過與消聲器傳遞損失測量結果和傳統混體邊界元方法計算結果的比較驗證了快速多極混體邊界元方法的正確性。與傳統混體邊界元方法相比，快速多極混體邊界元方法在保證計算精度的同時，能夠有效縮短大尺度問題的計算時間。將快速多極混體邊界元方法應用于計算穿孔消聲器的傳遞損失，結果表明，進出口管位置能夠影響兩通穿孔管消聲器的高頻消聲特性，隔板穿孔能夠改善三通穿孔管消聲器的中頻消聲性能。

穿孔消聲器； 傳遞損失； 混體邊界元方法； 快速多極算法； 計算效率

穿孔消聲器被廣泛應用于機械設備的噪聲控制。SELAMET等使用準一維方法對三通穿孔管消聲器進行了研究并分析了結構參數變化對傳遞損失的影響[1]。SELAMET等應用解析方法預測了直通穿孔管阻性消聲器的聲學性能[2]。JI使用子結構多域邊界元方法對直通穿孔管消聲器及具有共振腔的穿孔管消聲器進行了研究[3]，此后，多域邊界元方法被用于阻性消聲器的聲學性能預測[4]。JI等使用同樣的方法對三通穿孔管消聲器進行了計算，研究了穿孔率、穿孔部分長度等對消聲性能的影響[5]。FANG等[6]使用有限元方法對穿孔管消聲器進行了模態分析。解析方法適用于規則結構消聲器的聲學性能預測，對實際應用中具有復雜內部結構的消聲器無法應用，有限元方法和多域邊界元方法在理論上適用于任意結構。但也存在一些缺點，在應用多域邊界元方法時，必須按照邊界條件將內部結構劃分為許多子結構，再根據聲學變量的連續性條件在邊界上建立各子結構之間的聯系，對于復雜的內部結構，前處理過程勢必過于繁瑣，進而限制了其應用范圍。應用有限元方法進行穿孔消聲器的計算已經十分成熟，相應的商業軟件已經被廣泛應用，但是對于穿孔面，由于有限元方法一般采用傳遞阻抗建立穿孔面內外兩側的關系，所以一般要求兩個面的網格一一對應，對于具有多個穿孔面的消聲器，前處理也會較為繁瑣。WU等提出了一種混體邊界元方法[7-8]，此方法適合具有復雜內部結構消聲器的聲學性能計算，不需要人為劃分子結構，對于穿孔面，只需要建立一層面網格，因此非常適合具有較多穿孔結構消聲器的傳遞損失計算。

然而，由于傳統邊界元方法自身的局限性，在處理大尺度和高頻問題時對計算機內存的要求較高并會消耗較多的計算時間，近年來，快速多極算法的出現有效地克服了傳統邊界元方法的局限，應用快速多極邊界元方法計算大尺度聲學問題也取得了較大的進展[9-13]。

本文將混體邊界元方法與快速多極算法結合用于穿孔消聲器傳遞損失的計算，考察快速多極混體邊界元方法的計算精度和計算效率，研究穿孔管位置對兩通穿孔管消聲器傳遞損失的影響，分析穿孔擋板對三通穿孔消聲器聲學性能的影響。

1 計算方法

1.1 混體邊界元方法

直接混體邊界元方法源于傳統的子結構邊界元方法，將具有復雜內部結構的消聲器分成若干具有明確邊界的幾個部分，對每一部分使用邊界積分方程描述，然后，根據各部分的交界面的聲學參數連續條件，得到整體控制方程，交界面有兩個未知量時，超奇異積分方程被用來提供額外的方程。對于如圖1所示的直通穿孔管消聲器，混體邊界元方法可以表示為[7]

式中：P和Q分別為源點和場點；G=e-jk0r/4πrPQ，為格林函數；k為波數；z為空氣中的特性阻抗；ζ為穿孔阻抗。邊界條件R為常規邊界條件，包括進口邊界R1，出口邊界R2以及剛性壁，T為內部薄壁邊界，P為穿孔邊界。這里只列出了本文涉及到的邊界的直接混體邊界元的數學表達式，完整的控制方程可以從文獻[7]獲得，此處不再贅述。進口給定振速v=1，出口給定阻抗邊界條件，式(1)～(3)組成方程組：

(5)

其中

式中：E′只有源點P在穿孔邊界時存在，對剛性壁邊界其值為0，δ為Kronecker′s delta函數。求解式(5)，即可得到消聲器進出口節點的聲壓值用于傳遞損失的計算，本文中，使用的單元類型為常單元。

圖1 直通穿孔管消聲器Fig.1 Straight-through perforated tube silencer

1.2 快速多極混體邊界元方法

快速多極邊界元中格林函數可以表示為[9]

(6)

其中，

(7)

(8)

(9)

將式(9)對P求偏導，得到

(10)

在遠場計算中，源點與場點之間的影響系數存在多級傳遞關系，格林函數及其導數的多極子展開式可寫成：

(11)

(12)

同理，將式(12)對P求偏導，得到

(13)

其中,

(14)

(15)

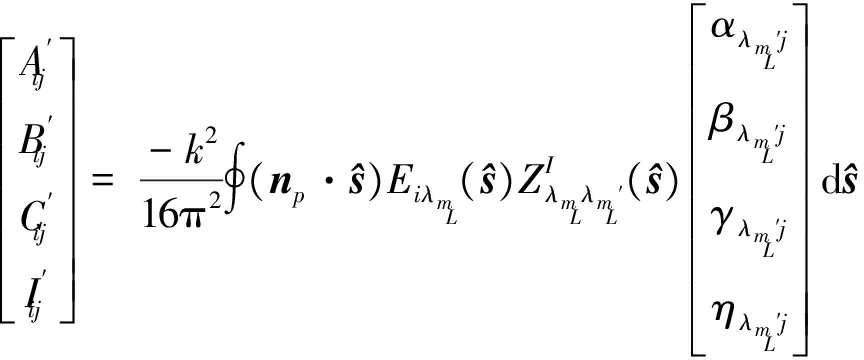
其中

(17)

(18)

(19)

(20)

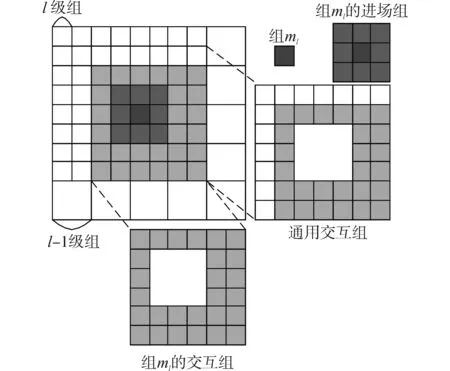
圖2 分級結構及通用交互組Fig.2 Hierarchical cell structure and common interaction cell

快速多極混體邊界元方法的計算過程如下：

1)遠場區域矩陣矢量積計算過程。

(21)

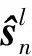
(22)

式中：Wn′n為插值方法(如拉格朗日法)的插值系數，Cml為組ml+1的父輩組所包含的子組集，此步計算將在向上傳遞的每一級中進行，直到級數為2。

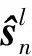
(23)

式中：Fml為組ml的交互組集。需要注意的是，為了簡便，在Tλmlλm′l的計算中，使用了通用交互組，其定義劃分見圖2，在迭代計算之前，根據格柵的位置關系，Tλmlλm′l已經計算完畢，迭代過程中只需根據距離關系調用。

(24)

可見，式(24)為遞推公式，由于在1級與2級之間不存在向下傳遞關系，因而有

(25)

此步計算將在向下傳遞的每一級中進行，直到級數為L-1。

⑤在最低級L，計算每個節點i的遠場影響系數φF,i，對應式(15)，計算公式為

(26)

對應式(16)，計算公式為

(27)

2)近場區域矩陣矢量積計算過程。

在最低級，若節點i所在組為mL，其近場組集為NmL，則近場矩陣矢量積即為計算節點i與所含節點間的影響系數，對奇異積分方程，計算公式為

(28)

對超奇異積分方程，計算公式為

(29)

最后，將近場影響系數與遠場影響系數相加得到每個節點的影響系數，經過迭代計算即可得到消聲器進出口節點的聲壓值。

2 算例驗證及計算效率分析

考慮一個直通穿孔管消聲器，對應圖1中尺寸為：r1=0.024 5 m，r2=0.082 2 m，l=0.257 2 m，穿孔率Ф=0.08，孔徑dh=0.002 49 m，壁厚tw=0.000 9 m。

穿孔阻抗表示為[14]

(30)

R和X的計算表達式：

(31)

(32)

式中：μ為空氣動力粘性系數，α為單一孔模型的端部修正系數，基于活塞驅動模型

(33)

式中：b和h為相鄰兩孔在兩個方向上的距離；ξ=dh/b，η=dh/h；式中第二個求和符號的上標“′”表示m和n不能同時為零，當m≠0且n≠0時，εmn=1，否則εmn=0.5；J1為第一類一階貝塞爾函數。

使用傳統混體邊界元方法與快速多極混體邊界元方法分別計算傳遞損失并與實驗值比較得到結果如圖3所示。可以看出，兩種方法的計算結果與實驗值吻合良好，驗證了快速多極混體邊界元方法的正確性。

圖3 直通穿孔管消聲器計算結果比較Fig.3 Transmission loss prediction of straight-through perforated silencer

下面從計算效率方面比較兩種方法，選定頻率為350Hz，在不同的網格數量的情況下比較計算時間，結果列于表1。所有計算均在Inteli7 3632QM, 2.2GHz的計算機上進行，從表中可以看出，在給定頻率下，隨著網格數量的增加，相比于傳統混體邊界元方法，快速多極混體邊界元方法的優勢越來越明顯，所以，在實際應用中，可以根據研究問題的尺度大小選擇適當的方法。

表1 直通穿孔管消聲器計算時間比較

Table 1 Computation time comparison of straight through perforated tube silencer

編號網格數MBEM/s傳統快速多極11448138427602220434613309342701402558744541626433921257542449361368569076—18975

3 計算結果分析

本節應用快速多極混體邊界元方法研究穿孔管位置及穿孔擋板對消聲器傳遞損失的影響。

首先，考慮如圖4所示的兩通穿孔管消聲器，膨脹腔長度均為l=0.257 2 m，穿孔壁厚tw=0.000 9 m，穿孔率Ф=0.08，孔徑dh=0.002 49 m，穿孔管半徑r1=0.02 m，膨脹腔半徑r2=0.1 m。對結構a，消聲器進口管處于軸線處，考慮兩種情況：a1出口管與進口管之間距離σ=0.06 m，a2出口管與進口管之間距離σ=0.05 m。對結構b，進出口穿孔管位于軸線兩側，考慮兩種情況：b1兩穿孔管距離軸線距離均為σ=0.06 m，b2兩穿孔管距離軸線距離均為σ=0.04 m。比較穿孔管位置的變化對兩種結構聲學性能的影響，結果如圖5所示。

可見，當進(出)口穿孔管處于軸線處時，傳遞損失曲線更接近軸對稱的直通穿孔管消聲器，消聲效果也更好。穿孔管位置的改變對a、b兩種結構的影響是不同的，對結構a，保持進口穿孔管處于軸線位置，改變處于非軸線位置的出口穿孔管的位置對傳遞損失有較大影響，在高頻處更加明顯。而對結構b，改變兩個處于非軸線位置的穿孔管的位置對

傳遞損失結果影響很小。

圖4 兩通穿孔管消聲器Fig.4 Two-pass perforated tube silencer

圖5 兩通穿孔管消聲器傳遞損失計算結果Fig.5 TL comparison of two-pass perforated tube silencer

在實際應用中，常采用在消聲器進出口添加剛性擋板構成三通穿孔管消聲器的形式，如圖6所示，穿孔管半徑r1=0.02 m，膨脹腔半徑r2=0.1 m，穿孔孔徑dh=0.002 49 m，穿孔壁及擋板壁厚tw=0.000 9 m，穿孔率Ф=0.08，la=0.1 m，lp=0.3 m，lb=0.15 m，σ=0.06 m。分別使用混體邊界元方法和快速多極混體邊界元方法計算傳遞損失，結果如圖7所示。同樣選定頻率為350 Hz，比較兩種方法的計算時間列于表2。

圖6 三通穿孔管消聲器Fig.6 Three-pass perforated tube silencer

一般三通穿孔管消聲器中的擋板是剛性薄壁，現在考慮將剛性薄壁結構替換為穿孔板，研究其對消聲器聲學性能的影響。在擋板分別為剛性壁面和穿孔板的情況下計算傳遞損失如圖8所示。在中低頻處，穿孔擋板三通穿孔消聲器的有效消聲頻率更寬，性能更好，應用穿孔擋板代替剛性壁擋板是有意義的。

圖7 三通穿孔管消聲器計算結果比較Fig.7 Transmission loss prediction results of three-pass perforated tube silencer

Table 2 Computation time comparison of three-pass perforated tube silencers

編號網格數MBEM/s傳統快速多極1551227933948227648460551399338864-18532

圖8 穿孔擋板對消聲器傳遞損失的影響Fig.8 Effect of perforated baffle on silencer TL

現在考慮穿孔擋板的物理參數變化對傳遞損失計算結果的影響，在穿孔率分別為0.03、0.08以及0.16的情況下計算傳遞損失，結果如圖9所示。

擋板穿孔率的變化對消聲器的傳遞損失有一定程度的影響，隨著穿孔率的增大，傳遞損失曲線向高頻方向移動，與此同時，在200～800 Hz的中頻范圍內，穿孔率的增大會改善消聲器的聲學性能。

下面考慮穿孔孔徑大小對傳遞損失的影響，在孔徑分別為0.002 49 m和0.004 98 m的情況下計算傳遞損失，結果如圖10所示。增大穿孔孔徑，會使傳遞損失曲線向低頻方向移動。

圖9 擋板穿孔率對三通穿孔消聲器傳遞損失的影響Fig.9 Effect of baffle porosity on TL of three-pass perforated tube silencer

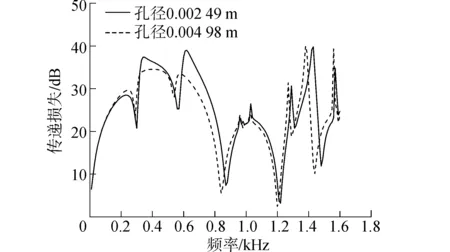
圖10 擋板孔徑對三通穿孔消聲器傳遞損失的影響Fig.10 Effect of baffle hole diameter on TL of three-pass perforated tube silencer

在穿孔擋板的情況下，考慮三通穿孔管消聲器左右兩端膨脹腔長度對聲學性能的影響，改變膨脹腔長度，計算結果如圖11所示。由圖可知，增大左右膨脹腔的長度會使傳遞損失曲線向低頻方向移動。

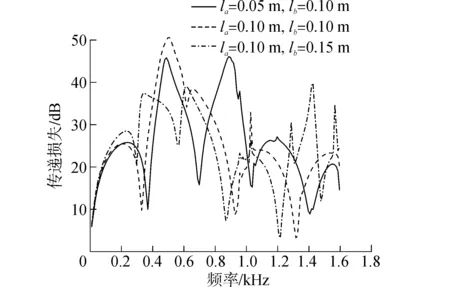
圖11 膨脹腔長度對三通穿孔消聲器傳遞損失的影響Fig.11 Effect of inlet/outlet expansion chamber length on TL of three-pass perforated tube silencer

4 結論

1)快速多極混體邊界元方法在能夠保證計算精度的情況下，對大尺度高頻問題能夠有效地減少計算時間，在實際應用中，可以根據研究問題的情況選擇適當的方法進行計算。

2)當進口位于軸線處時，消聲器的聲學性能更好，出口穿孔管的位置變化對計算結果的影響應該給予考慮，而當進口位于非軸線處時，進出口穿孔管距離的變化對傳遞損失影響很小，基本可以忽略不計。

3)使用穿孔板代替三通穿孔消聲器中的剛性隔板能改善其中低頻的聲學性能，減小穿孔板穿孔孔徑、增大穿孔率以及進出口膨脹腔的長度會使傳遞損失曲線向高頻方向移動。

[1]SELAMET A, EASWARAN V, FALKOWSKI A G. Three-pass mufflers with uniform perforations[J]. The journal of the acoustical society of America, 1999, 105(3): 1548-1562.

[2]SELAMET A, XU M B, LEE I J, et al. Analytical approach for sound attenuation in perforated dissipative silencers with inlet/outlet extensions[J]. The journal of the acoustical society of America, 2005, 117(4): 2078-2089.

[3]JI Z L. Acoustic attenuation characteristics of straight-through perforated tube silencers and resonators[J]. Journal of computational acoustics, 2008, 16(03): 361-379.

[4]JI Z L. Boundary element acoustic analysis of hybrid expansion chamber silencers with perforated facing[J]. Engineering analysis with boundary elements, 2010, 34(7): 690-696.

[5]JI Z L, SELAMET A. Boundary element analysis of three-pass perforated duct mufflers[J]. Noise control engineering journal, 2000, 48(5): 151-156.

[6]FANG Z, JI Z L. Finite element analysis of transversal modes and acoustic attenuation characteristics of perforated tube silencers[J]. Noise control engineering journal, 2012, 60(3): 340-349.

[7]WU T W, CHENG C Y R, ZHANG P. A direct mixed-body boundary element method for packed silencers[J]. The Journal of the acoustical society of America, 2002, 111(6): 2566-2572.

[8]WU T W, WAN G C. Muffler performance studies using a direct mixed-body boundary element method and a three-point method for evaluating transmission loss[J]. Journal of vibration and acoustics, 1996, 118(3): 479-484.

[9]SAKUMA T, YASUDA Y. Fast multipole boundary element method for large-scale steady-state sound field analysis. Part I: setup and validation[J]. Acta acustica united with acustica, 2002, 88(4): 513-525.

[10]WU H, LIU Y, JIANG W. A low-frequency fast multipole boundary element method based on analytical integration of the hypersingular integral for 3D acoustic problems[J].Engineering analysis with boundary elements, 2013, 37(2): 309-318.

[11]LI S, HUANG Q. A fast multipole boundary element method based on the improved Burton-Miller formulation for three-dimensional acoustic problems[J]. Engineering analysis with boundary elements, 2011, 35(5): 719-728.

[12]王雪仁, 季振林. 快速多極子聲學邊界元法及其應用研究[J]. 哈爾濱工程大學學報, 2007, 28(7): 752-757. WANG Xueren, JI Zhenlin. Fast multipole acoustic BEM and its application[J]. Journal of Harbin Engineering University, 2007, 28(7): 752-757.

[13]吳海軍, 蔣偉康, 魯文波. 三維聲學多層快速多極子邊界元及其應用[J]. 物理學報, 2012, 61(5): 54301-054301. WU Haijun, JIANG Weikang, LU Wenbo. Multilevel fast multipole boundary element method for 3D acoustic problems and its applications[J]. Acta physica sinica, 2012, 61(5): 54301-054301.

[14]JI Z L, FANG Z. On the acoustic impedance of perforates and its application to acoustic attenuation predictions for perforated tube silencers[C]//Proceedings of INTER-NOISE. Osaka, 2011(5): 2803-2813.

本文引用格式：

楊亮，季振林. 穿孔消聲器聲學計算的快速多極混體邊界元法[J]. 哈爾濱工程大學學報， 2017， 38(8): 1247-1253.

YANG Liang, JI Zhenlin. Acoustic computation of perforated silencers by fast multi-pole mixed-body boundary element method[J]. Journal of Harbin Engineering University， 2017， 38(8): 1247-1253.

Acoustic computation of perforated silencers by fast multi-pole mixed-body boundary element method

YANG Liang, JI Zhenlin

(School of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China)

To improve computation efficiency and extend the computation frequency range, the mixed-body boundary element method (MBEM) was combined with the fast multi-pole algorithm to evaluate the acoustic attenuation performance of perforated silencers. The correction of fast MBEM was validated by comparing the measuring result of transmission loss with the computation result of traditional MBEM. The fast multi-pole mixed-body boundary element method (FMMBEM) may efficiently save computational time for large-scale acoustic problems without affecting accuracy. The FMMBEM was then employed to predict the transmission loss of perforated silencers. Predicted results showed that the locations of inlet and outlet tubes may affect the acoustic attenuation characteristics of the two-pass perforated tube silencer at higher frequencies, while the perforation on bulkhead(s) may improve the acoustic attenuation performance of three-pass perforated tube silencer in the middle frequency range.

perforated silencer; transmission loss; mixed body boundary element method; fast multi pole algorithm; computation efficiency

2016-06-14.

日期：2017-04-26.

國家自然科學基金項目(11174065).

楊亮(1989-), 男, 博士研究生； 季振林(1965-), 男, 教授, 博生生導師.

季振林, E-mail:jizhenlin@hrbeu.edu.cn.

10.11990/jheu.201606040

TB535

A

1006-7043(2017)08-1247-07

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20170426.1801.066.html