讓學生多維度思考問題
——以一道練習題的教學為例

文︳郁晶晶

讓學生多維度思考問題
——以一道練習題的教學為例

文︳郁晶晶

在學完比的應用后，學生學習的勁頭很足，對于一般的按比例分配的題目，做題的興致很高，解答正確率高。如果遇上稍難的題目，學生會不會運用所學的知識順利解答呢？為了培養學生靈活運用知識解決實際問題的能力，在整理與復習課上，我給學生出示了一道綜合應用題：甲、乙兩箱中粉筆盒數之比是5∶1，如果從甲箱里取出12盒放入乙箱中，甲、乙兩箱中粉筆盒數的比變為7∶5，那么甲、乙兩箱中共有粉筆多少盒？

這道題有一定的難度，我先讓學生獨立思考，然后一起探討如何解題。在思考的過程中，很多平時一拿到題目就動筆寫的學生輕蹙眉頭，不知從何處下手；還有的學生不停地在草稿紙上寫寫、畫畫。10分鐘后，有學生終于展顏，有了答案。于是我讓解出答案的學生上臺匯報。

生1的方法是：不管甲、乙兩箱中的粉筆盒數怎么變化，粉筆的總盒數是不變的，因此，可以設甲、乙兩箱共有粉筆x盒。變化前，甲、乙兩箱中粉筆盒數之比為5∶1，可知甲箱中粉筆盒數占了總盒數的，所以甲箱中有粉筆x盒；當從甲箱取出12盒放入乙箱后，甲、乙兩箱中粉筆的盒數之比為7∶5，可知甲箱中粉筆的盒數占了總盒數的，這時甲箱中有粉筆盒。根據等量關系式：變化前甲箱的粉筆盒數-變化后甲箱的粉筆盒數=12，我們可以列出方程：x-x=12，解得x=48。所以甲、乙兩箱中共有粉筆48盒。

這一方法是借助于按比例分配的思路，根據題意列出方程解題，解題的思路清晰，計算相對容易，其他學生容易理解。

生1的方法剛講完，生2就迫不及待地匯報了他的方法，他是用比來解的。

生2的方法是：因為變化前甲、乙兩箱中粉筆的盒數比是5∶1，那可以設乙箱原有粉筆x盒，則甲箱粉筆為5x盒，根據“甲箱里取出12盒放入乙箱后，甲、乙兩箱中粉筆盒數的比變為7∶5”這一關鍵句來列方程。等量關系式為：（甲箱原有的粉筆盒數-12）∶（乙箱原有的粉筆盒數+12）=7∶5，列出方程為（5x-12）∶（x+12）=7∶5。

面對這一方程，學生們一籌莫展，都不會計算。于是我引導學生回顧所學的知識：“兩個數的比就是什么？”生答：“兩個數的比就是兩個數相除。”學生茅塞頓開，反應快的馬上把算式寫成了（5x-12）÷（x+12）=7÷5，解出x=8，則5x=5×8=40，40+8=48（盒）。所以甲、乙兩箱中共有粉筆48盒。

還有學生指出可以運用比例的基本性質“兩內項之積等于兩外項之積”來解：（5x-12）∶（x+12）=7∶5，則有（x+12）×7=（5x-12）×5，兩邊分別運用乘法分配律去掉括號，得到7x+84=25x-60，再根據等式的性質求出x=8。

這一方法所列方程計算時有點復雜，但是學生能夠在老師的啟發下根據比與除法的聯系、比例的基本性質和等式的性質進行解答，也非常不錯。

當我把期待和贊許的目光投向全班學生時，精彩又來了——

生3的方法是：不管甲箱和乙箱中的粉筆數量怎么變化，兩箱粉筆的總數量不變，就是說單位“1”沒變，只是變化前和變化后甲箱與乙箱中的粉筆盒數所占的分率發生了變化，甲箱中的粉筆盒數變化前占了總數的，變化后占了總數。之所以會有這樣的變化，是因為甲箱取出12盒給了乙箱，只要找到12盒這個比較量所對應的分率就可以知道單位“1”的量是多少。很多學生滿臉疑惑，似懂非懂。生3根據題目中的量率對應關系畫出線段圖（如圖1），指著線段圖中甲“取出12盒”這一部分說：12所對應的分率正好是（-），也就是說，已知總數的（-）是12，求總數是多少，可以用除法計算，列式為：12÷（），答案為48盒。

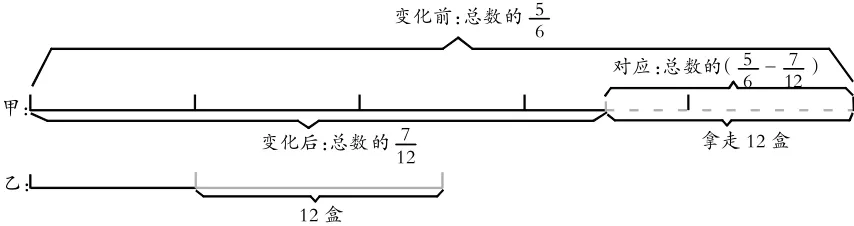
圖1

這種解法干凈利落，思路非常清晰。聽他對照線段圖分析完后，原來云里霧里的學生眉頭漸漸舒展開來。

此時，生4興奮地站起來說從生3的方法中得到了啟發。他一邊說一邊畫圖（如圖2）：變化前甲乙兩箱中的粉筆盒數比為5∶1，即乙箱中的粉筆盒數占總數的；甲箱取出12盒給乙箱后，兩箱中的粉筆盒數之比為7∶5，即乙箱中的粉筆盒數占總數的；乙箱新增的這“12盒”對應于總數的分率為（-）。

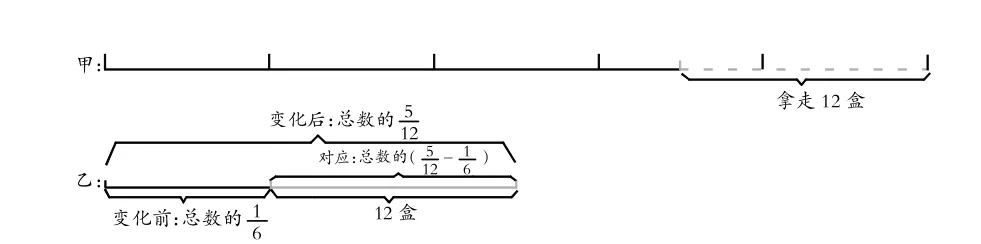
圖2

學生紛紛點頭，沒等生4說完，就寫出了算式：12÷（），算出得數為48。

當學生沉浸在會心一悟時，我又要求學生對照板書，找出幾種方法的異同，溝通方法之間的聯系。學生積極交流、思辨，課堂呈現出從未有過的活躍。

一道綜合題，學生居然得出了多種解法，我在驚嘆之余，頗有感觸。

綜合題對相當一部分學生來說是有挑戰性的。教師要先給學生嘗試的機會，讓他們有獨立思考的時間。對很多學生來說，只有思維碰壁后，才會有想要學習、想要掌握、想要傾聽的意愿。

在解決這道綜合題的過程中，正是由于教師給足了學生思考的時間，學生得出了不同的解題方法。教師及時引導學生進行對比、辨析，溝通了這些方法之間的內在聯系，使訓練效果達到最大化。尤其值得一提的是，方法三采用了量率對應的方法解決問題。運用這一方法把比的應用問題轉化成分數乘除法應用題，實現比與分數之間的快速轉化是前提，理清量率之間的對應關系是關鍵，利用線段圖幫助理解題意是一種重要策略。從案例中我們可以發現，學生理解方法三是有困難的，而借助線段圖，較好地實現了比與分數之間的轉化、量率對應關系的建立和基本數量關系的表達。由于受到方法三的思路的啟發，有學生甚至自然遷移出另一種方法。

數學是鍛煉思維的體操，是啟迪智慧的鑰匙。培養學生的數學思維是數學教學的基本任務之一。在教學中，教師要讓學生多維度思考問題，鼓勵學生進行探討，把思考引向深入。本節課雖然教學時間延長了20分鐘，但學生的思維是活躍的。他們在不斷探索的過程中找到了方法，收獲了自信，極大地增強了成功感，解題能力也得到了提高。

（作者單位：江蘇省海門市海南小學）