淺談教學中創(chuàng)造性思維的培養(yǎng)

王建春

(江蘇省邳州市八義集高級中學，江蘇 徐州 221361)

淺談教學中創(chuàng)造性思維的培養(yǎng)

王建春

(江蘇省邳州市八義集高級中學，江蘇 徐州 221361)

在新課程的教育理念下，培養(yǎng)學生積極主動、勇于探索的學習能力已經(jīng)成為一個重要課題，如何培養(yǎng)學生的創(chuàng)造性思維成為關(guān)鍵.創(chuàng)造性的思維必須有創(chuàng)新意識和創(chuàng)新精神做支撐，這就要求廣大教師在新理念的指導下創(chuàng)新教學模式，改革教學方式，提升教學質(zhì)量，還原教育本質(zhì)，提升學生的學科核心素養(yǎng).

創(chuàng)造性思維；獨立性； 綜合性

一、主動發(fā)展 培養(yǎng)獨立性思維

素質(zhì)教育的工作重點就是要培養(yǎng)受教育者的創(chuàng)新精神和實踐能力.所以在教學實踐中，要面向全體學生，“讓學生主動發(fā)展”，有意識地鼓勵學生養(yǎng)成獨立思維的意識和習慣，敢于發(fā)表獨立見解，并付諸實踐.

比如《必修2》32頁有這樣一個例題：

例1 已知：a∥b,a⊥α，求證：b⊥α．

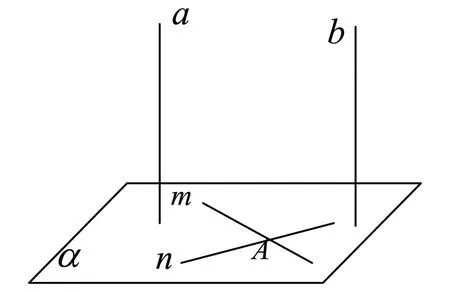
這道題目教材是通過定義法證明b垂直與平面α內(nèi)的任意一條直線，我在課堂講解這道例題時，除了課本上的方法外，積極引導學生思考其他證明方法.現(xiàn)把學生的一種證法整理如下：

證明：在平面α內(nèi)作兩條相交直線m,n且m∩n=A.

∵直線a⊥α，

∴a⊥m,a⊥n(直線與平面垂直的定義知).

又∵a∥b，∴b⊥m，b⊥n．

又∵m?α，n?α，m∩n=A,∴b⊥α.

再比如在學習“§1.2.1平面的基本性質(zhì)”中的公理2“如果兩個平面有一個公共點，那么它們還有其他公共點，這些公共點的集合是經(jīng)過這個公共點的一條直線”時，我隨手拿起兩本書作為平面模型讓學生體會兩個平面的公共點，我故意將其中一本書的端點與另一本書的表面接觸，讓學生感受到發(fā)散思維：兩個平面會不會只有一個公共點？這時候?qū)W生分組開始討論.我再利用兩張紙演示“平面的無限延伸性”，其中一張紙帶有縫隙，再次演示一個交點的情況，順勢將一張紙插到另一張的縫隙中，這會讓學生有深刻的印象，培養(yǎng)學生創(chuàng)造性思維.

二、全面發(fā)展，培養(yǎng)綜合性思維

數(shù)學課堂中，要積極培養(yǎng)學生的綜合性思維，只有在在教學實踐中積極運用綜合思維，才能提高學生的綜合能力和學科素養(yǎng).

比如這樣一道題：如果二次函數(shù)y=mx2+(m-3)x+1圖象與x軸的交點至少有一個在原點的右側(cè)，試求m的取值范圍.

分析 這道題要是直接求解需要從三個方面討論，這樣非常冗繁，此時可以引導學生進行逆向思維，從反面思考，考慮函數(shù)圖象與x軸的交點均在原點的左側(cè)可得m≥9，其反面m<9，再考慮Δ≥0,m≠0，可得m的取值范圍是m≤1且m≠0(解略).

2.思維的“類比推理”.思維也像數(shù)學的“類比推理”一樣：尋求事物之間的關(guān)系，類比從特殊到特殊.

三、創(chuàng)造想象，培養(yǎng)跳躍性思維

愛因斯坦指出：“想象力比知識更重要，因為知識是有限的，而想象力概括著世界上的一切，嚴格地說，想象力是科學研究中的實在因素.”教師要在民主、平等、輕松的教學情境中，實現(xiàn)創(chuàng)造性的學習活動，并有針對性地進行跳躍性思維的訓練.

例如：在正四棱錐O-ABCD中，E、F分別為AD，BC中點，且OE⊥OB,P為平面OEF與此正四棱錐內(nèi)切單位球球面的交線上一動點，求P點到三角形OEF三個頂點距離平方和的最大值與最小值.

分析 此題分兩步考慮.第一步是確定△OEF的形狀，第二步是對△OEF內(nèi)切單位圓上動點求“距離”的最大值與最小值.

猜測：根據(jù)經(jīng)驗及題目條件，憑直覺將會預(yù)感到這個△OEF是一個等腰直角三角形.通過證明，易得△OEF是等腰直角三角形.之后只要以O(shè)為原點，OE、OF為坐標軸建立直角坐標系，問題即趨于明朗化.

教學中，教師把課堂還給學生，相信學生，讓學生“先發(fā)制人”，大膽直覺、猜想，思維“完美跳躍”，這才是走向成功的捷徑.

四、一題多解，培養(yǎng)發(fā)散性思維

散性思維是創(chuàng)造性的思維，要求思維朝著各個方向發(fā)散開去，達到流暢、變通、獨特.

比如：正三角形兩個頂點的坐標是A(1,0),B(2,1),第三個頂點C在第一象限，求C點坐標.

此題比較簡單，但如果能就此例組織一題多解教學，那么，對培養(yǎng)發(fā)散性思維能力，將會收益匪淺.

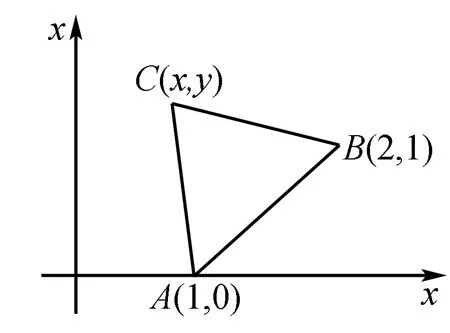
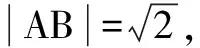
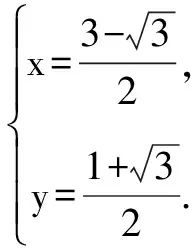
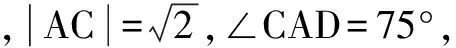
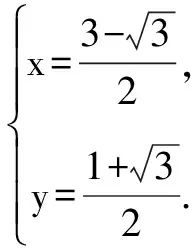
解法4 (參數(shù)法)(理)

解法5 (極坐標法)(理)

在平時教學中，教師應(yīng)幫助學生樹立數(shù)學精神，求真精神、創(chuàng)新精神，領(lǐng)悟數(shù)學的真諦，也許這才是學生受益一生的東西.

[1]李孝成.中學數(shù)學教學中培養(yǎng)學生創(chuàng)造性思維能力[J].數(shù)學教學通訊，2012(24).

[2]李志.物理教學中對學生創(chuàng)造性思維的培養(yǎng)[J].數(shù)理化解題研究，2016(36).

[責任編輯：楊惠民]

2017-06-01

王建春(1983.05-)，男，黑龍江省伊春人，中學一級，本科學歷，從事數(shù)學課堂的興趣培養(yǎng).

G632

B

1008-0333(2017)19-0025-02