H ilber-Hughes-Tay lor-α法在接觸約束多體系統(tǒng)動(dòng)力學(xué)中的應(yīng)用?
郭晛 章定國?陳思佳
1)(南京理工大學(xué)理學(xué)院,南京 210094)
2)(浙江大學(xué)寧波理工學(xué)院,寧波 315100)
H ilber-Hughes-Tay lor-α法在接觸約束多體系統(tǒng)動(dòng)力學(xué)中的應(yīng)用?
郭晛1)章定國1)?陳思佳2)
1)(南京理工大學(xué)理學(xué)院,南京 210094)
2)(浙江大學(xué)寧波理工學(xué)院,寧波 315100)
(2017年3月12日收到;2017年6月7日收到修改稿)
以柔性梁在重力作用下繞轉(zhuǎn)動(dòng)鉸做大范圍定軸轉(zhuǎn)動(dòng),并與剛性平面發(fā)生碰撞這一動(dòng)力學(xué)過程為例,對(duì)Hilber-Hughes-Taylor(HHT-α)法在求解含接觸約束的柔性多體系統(tǒng)動(dòng)力學(xué)方程時(shí)的數(shù)值特性進(jìn)行了研究.系統(tǒng)運(yùn)動(dòng)過程的全局動(dòng)力學(xué)仿真由常微分方程組和微分-代數(shù)方程組的數(shù)值求解構(gòu)成.柔性梁在無碰撞階段系統(tǒng)動(dòng)力學(xué)方程是一組常微分方程組.采用接觸約束法模擬接觸約束過程,系統(tǒng)的動(dòng)力學(xué)方程為指標(biāo)3的微分-代數(shù)方程組.采用HHT-α法對(duì)的該微分-代數(shù)方程組進(jìn)行求解,并與Baumgarte違約修正法進(jìn)行比較.分析了HHT-α法自由參數(shù)和違約修正常數(shù)對(duì)計(jì)算效率、動(dòng)力學(xué)響應(yīng)和系統(tǒng)機(jī)械能的影響,并對(duì)數(shù)值積分方法對(duì)模態(tài)截?cái)鄶?shù)的敏感度以及速度約束和加速度約束的違約程度進(jìn)行了分析.結(jié)果表明,違約修正常數(shù)對(duì)仿真結(jié)果影響非常明顯,而HHT-α法的自由參數(shù)α對(duì)動(dòng)力學(xué)響應(yīng)的影響較小,從而避免了違約修正常數(shù)對(duì)數(shù)值積分結(jié)果的影響.HHT-α法的自由參數(shù)α可以消除碰撞高頻模態(tài)的影響.
柔性多體系統(tǒng),碰撞,HHT-α法,Baumgarte違約修正
1 引 言
復(fù)雜柔性多體系統(tǒng)在操作運(yùn)行中往往會(huì)出現(xiàn)接觸、碰撞現(xiàn)象,對(duì)這類系統(tǒng)進(jìn)行全局動(dòng)力學(xué)仿真時(shí),高效率、高精度和高穩(wěn)定性的數(shù)值計(jì)算方法是基本前提.隨著柔性多體系統(tǒng)動(dòng)力學(xué)的不斷發(fā)展,處理該類方程組的數(shù)值積分方法也得到大量研究[1?21].Petzold[1]對(duì)指標(biāo)3微分代數(shù)方程組的數(shù)值求解方法進(jìn)行了綜述;Hilber,Hughes和Taylor[2]引入自由參數(shù)α (HHT-α), 在Newmark方法[3]基礎(chǔ)上提出了HHT法;Cardona和Géradin[4]將Newmark法和HHT-α 法推廣到了指標(biāo)3帶約束動(dòng)力學(xué)方程的數(shù)值求解中;Negrut等[5,6]將HHT-α法應(yīng)用于柔性多體系統(tǒng)動(dòng)力學(xué)分析;Chung和Hulbert[7]將基于HHT法提出的廣義-α法用于結(jié)構(gòu)動(dòng)力學(xué)有限元分析;Hussein等[8]研究了HHT-I3法在柔性多體系統(tǒng)動(dòng)力學(xué)仿真中的可調(diào)數(shù)值阻尼特性等;Shabana和Hussein[9]提出了使用Newmark法對(duì)獨(dú)立坐標(biāo)積分的雙循環(huán)隱式積分方法;Husssein和Shabana[10]研究了基于HHT法的雙循環(huán)隱式積分法中步長(zhǎng)的選取原則.國內(nèi)方面,洪嘉振[11]推動(dòng)了計(jì)算多體系統(tǒng)動(dòng)力學(xué)這一分支學(xué)科在國內(nèi)的發(fā)展;王琪和陸啟韶[12]總結(jié)了Lagrange方程的數(shù)值算法;丁潔玉和潘振寬[13]針對(duì)指標(biāo)3完整約束多體系統(tǒng)動(dòng)力學(xué)微分-代數(shù)方程,結(jié)合約束投影方法提出廣義α-S投影法;馬秀騰等[14,15]從能量角度研究了Newmark方法和HHT-α方法求解約束力學(xué)系統(tǒng)指標(biāo)2運(yùn)動(dòng)方程時(shí)的數(shù)值性能;張樂和章定國[16,17]提出了基于向后差分法和隱式龍格庫塔法的兩種新雙循環(huán)隱式積分方法;闞子云等[18]基于SiPESC平臺(tái)開發(fā)了開放式多體系統(tǒng)動(dòng)力學(xué)仿真算法軟件,綜合比較研究了Newmark法、HHT-I3 法、Generalize-α方法、Bathe方法和祖沖之類Symplectic方法.
HHT-α法作為一種二階隱式數(shù)值積分方法,具有控制數(shù)值阻尼耗散的良好特性,在柔性多體系統(tǒng)動(dòng)力學(xué)方程求解中具有重要應(yīng)用價(jià)值.雖然關(guān)于HHT-α法的研究已展開大量工作,但是針對(duì)復(fù)雜多體系統(tǒng)的數(shù)值求解依然存在諸多問題.如柔性多體系統(tǒng)碰撞問題中,由于碰撞過程具有持續(xù)時(shí)間短、作用強(qiáng)度大、動(dòng)力學(xué)方程強(qiáng)非線性和高度耦合等特點(diǎn),使得數(shù)值積分求解困難極大.此外,同時(shí)滿足位置、速度和加速度約束方程也是求解的一個(gè)難點(diǎn),且由于高階頻率被激發(fā),自由參數(shù)對(duì)碰撞響應(yīng)和系統(tǒng)能量均會(huì)產(chǎn)生不同影響.
本文針對(duì)柔性多體系統(tǒng)動(dòng)力學(xué)中典型的中心剛體-柔性懸臂梁系統(tǒng),以柔性梁在重力場(chǎng)下繞轉(zhuǎn)動(dòng)鉸做大范圍定軸轉(zhuǎn)動(dòng),且與剛性平面發(fā)生碰撞這一動(dòng)力學(xué)過程為例,對(duì)HHT-α法在求解含接觸約束的柔性多體系統(tǒng)動(dòng)力學(xué)方程時(shí)的數(shù)值特性進(jìn)行了研究.系統(tǒng)運(yùn)動(dòng)過程的全局動(dòng)力學(xué)仿真包括:在無碰撞階段,系統(tǒng)的動(dòng)力學(xué)方程為一組常微分方程組(ordinary diff erential equations,ODEs);采用接觸約束法模擬系統(tǒng)接觸碰撞過程,系統(tǒng)的動(dòng)力學(xué)方程為一組指標(biāo)3的微分-代數(shù)方程組(differential algebraic equations,DAEs).可見在全局動(dòng)力學(xué)仿真中待求方程的維數(shù)會(huì)隨接觸狀態(tài)變化而產(chǎn)生突變,使得數(shù)值計(jì)算難度大大增加,因此必須對(duì)含接觸約束的全局動(dòng)力學(xué)方程的數(shù)值特性進(jìn)行分析.其中,指標(biāo)3的DAEs常見求解方法是Baumgarte違約修正法[19?21].Baumgarte違約修正法屬于增廣法,可以通過選擇修正系數(shù)滿足約束方程并將DAEs化為微分方程進(jìn)行求解.然而,其修正系數(shù)的選擇沒有通用方法,人為憑經(jīng)驗(yàn)選取修正系數(shù)是造成該類方法數(shù)值計(jì)算穩(wěn)定性問題的主要原因.本文選擇HHT-α法來求解該類動(dòng)力學(xué)DAEs.首先對(duì)指標(biāo)3的DAEs降指標(biāo)處理得到指標(biāo)2的超定(overdeterMined)微分-代數(shù)方程組(ODAEs),再引入Gear-Gupta-Leimkuhler(GGL)法化ODAEs為DAEs后再使用HHT法進(jìn)行數(shù)值求解.通過與BauMgarte違約修正法的比較,分析HHT-α法自由參數(shù)α、違約修正常數(shù)以及假設(shè)模態(tài)的模態(tài)截?cái)鄶?shù)等因素對(duì)數(shù)值計(jì)算結(jié)果的影響,以此研究HHT-α法在求解這類動(dòng)力學(xué)方程組時(shí)的數(shù)值特性.同時(shí)仿真結(jié)果也與連續(xù)接觸力法(the continuous contact forcemethod,CCFM)[22]建立的碰撞動(dòng)力學(xué)微分方程組的仿真結(jié)果進(jìn)行比較,驗(yàn)證HHT-α法求解DAEs時(shí)仿真結(jié)果的正確性.
2 柔性多體系統(tǒng)動(dòng)力學(xué)建模
2.1 物理模型
考慮圖1的柔性梁系統(tǒng):柔性梁繞轉(zhuǎn)動(dòng)鉸O在重力場(chǎng)下做大范圍定軸轉(zhuǎn)動(dòng),假設(shè)梁上一點(diǎn)P與水平剛性O(shè)-X Z平面上某點(diǎn)Q發(fā)生碰撞.假設(shè)柔性梁為平面細(xì)長(zhǎng)Euler-Bernoulli梁,變形時(shí)梁的橫截面仍然保持為平面且與中軸線垂直.柔性梁的長(zhǎng)度為L(zhǎng),質(zhì)量密度為ρ,彈性模量為E,橫截面積為S,截面慣性矩為I,轉(zhuǎn)動(dòng)鉸處的驅(qū)動(dòng)力矩為τ.使用浮動(dòng)坐標(biāo)系O-xy相對(duì)于慣性坐標(biāo)系O-XY的轉(zhuǎn)動(dòng)角θ描述梁的大范圍運(yùn)動(dòng),在浮動(dòng)坐標(biāo)系中描述梁的變形運(yùn)動(dòng).
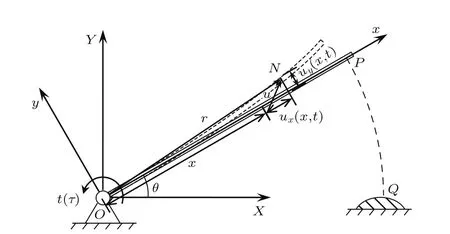
圖1 柔性梁碰撞Fig.1.The iMpact Model of the fl exib le beam.
采用假設(shè)模態(tài)法描述柔性梁的變形,柔性梁軸向變形位移ux和橫向變形位移uy的表達(dá)式[22?24]為
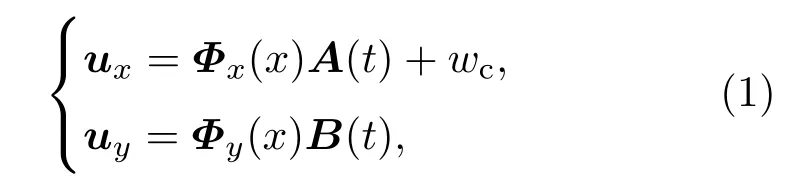
式中,Φx(x)∈ R1×N和Φy(x)∈ R1×N分別為梁的軸向振動(dòng)和橫向振動(dòng)的模態(tài)函數(shù)行矢量,A(t)∈ RN×1和B(t)∈ RN×1分別為軸向振動(dòng)和橫向振動(dòng)的模態(tài)坐標(biāo)列矢量,N為模態(tài)截?cái)鄶?shù).H(x)∈RN×N是耦合形函數(shù)矩陣,ux中Wc=Δ?BT(t)H(x)B(t)是橫向彎曲變形引起的梁軸向縮短量,稱為非線性耦合變形量.
2.2 無碰撞的柔性多體系統(tǒng)動(dòng)力學(xué)建模
取廣義坐標(biāo)q=(θ,AT,BT)T,由第二類拉格朗日方程得到系統(tǒng)在重力場(chǎng)下繞轉(zhuǎn)動(dòng)鉸做大范圍運(yùn)動(dòng)時(shí)的剛-柔耦合動(dòng)力學(xué)微分方程:
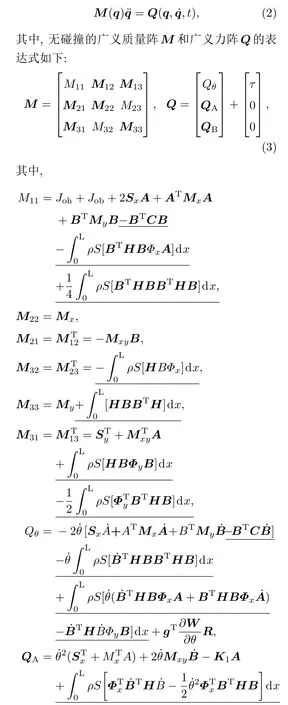
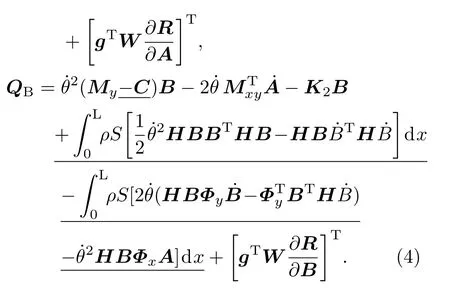
(4)式常系數(shù)矩陣Joh,Job,Sx,Sy,C,Mx,My,Mxy,K1,K2,g,W和R詳見文獻(xiàn)[22—24],其中下劃線項(xiàng)是由于變形位移中引入非線性二階耦合變形量Wc而產(chǎn)生的.
2.3 含接觸約束的柔性多體系統(tǒng)動(dòng)力學(xué)建模
2.3.1 接觸約束法建模
含接觸約束的動(dòng)力學(xué)建模方法中,采用接觸約束法(the contact constraint method,CCM)可無需人為附加參數(shù),無相互嵌入假設(shè),且碰撞力依據(jù)動(dòng)力學(xué)方程求解得到,較符合實(shí)際情況.故本文使用接觸約束法來模擬接觸碰撞過程.然而,無碰撞時(shí)系統(tǒng)的動(dòng)力學(xué)方程為ODEs的形式,碰撞過程中由于約束方程的引入使動(dòng)力學(xué)方程突變?yōu)镈AEs的形式,碰撞結(jié)束后動(dòng)力學(xué)方程再次變?yōu)镺DEs形式.
取廣義坐標(biāo)q=(θ,AT,BT)T,由第二類拉格朗日方程得到系統(tǒng)發(fā)生碰撞時(shí)的剛-柔耦合動(dòng)力學(xué)微分方程:
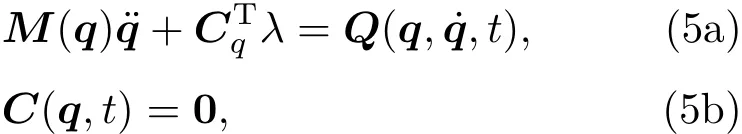
(5a)式中,M為無碰撞時(shí)的廣義質(zhì)量矩陣,Q為無碰撞時(shí)的廣義力列陣,C為位置約束方程,Cq= ?C/?q為約束Jacobian矩陣,λ為L(zhǎng)agrange乘子即接觸約束反力,也就是碰撞力.
2.3.2 連續(xù)接觸力法建模
選擇非線性彈簧阻尼模型來模擬接觸碰撞過程,用非線性阻尼力來反映碰撞過程中系統(tǒng)的能量損失,在低速碰撞過程仿真較為準(zhǔn)確.非線性彈簧阻尼模型是以Hertz接觸理論為基礎(chǔ),這里采用總體法向碰撞力以添加非線性阻尼.碰撞力大小的表達(dá)式為
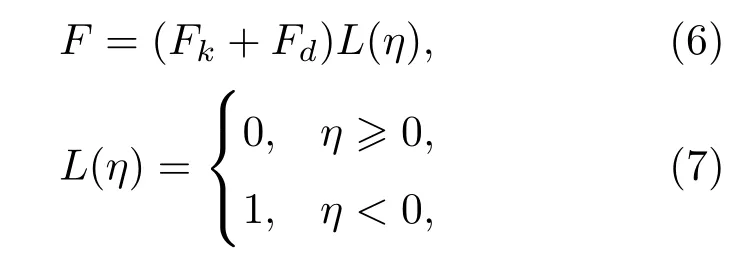
式中,η是碰撞體間嵌入量,相互嵌入為負(fù);L(η)是邏輯函數(shù),用以判斷接觸與否.Fk是法向彈性接觸力,Fd是非線性阻尼力,這里取表達(dá)式為
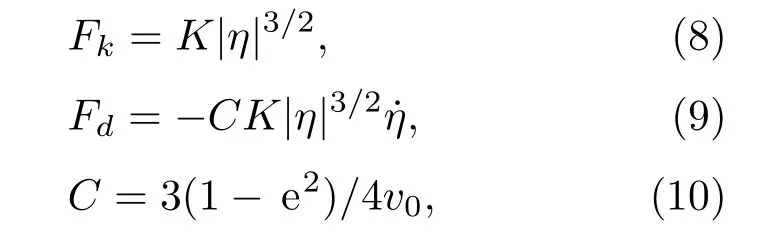
式中,K為接觸剛度,C為阻尼系數(shù),e為恢復(fù)系數(shù),˙η為碰撞點(diǎn)之間的嵌入速度,v0為碰撞點(diǎn)初始相對(duì)速度.
3 兩種數(shù)值求解方法
3.1 BauMgarte違約修正法
在無碰撞階段,使用四階AdaMs預(yù)估-校正法對(duì)動(dòng)力學(xué)方程(2)進(jìn)行求解.對(duì)于碰撞階段的DAEs,用加速度約束方程=0替代位置約束方程C=0來對(duì)DAEs進(jìn)行處理.即預(yù)先將(5b)式對(duì)時(shí)間t求兩次導(dǎo)數(shù)得到(11)式,記為CqΔ=γ.
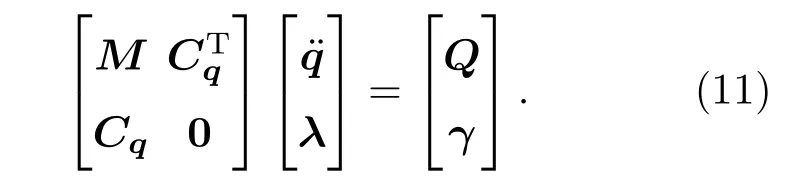
此時(shí),若直接對(duì)(11)式進(jìn)行求解得到的廣義坐標(biāo)滿足加速度約束方程=0,而位置約束方程C=0和速度約束方程=0則難以保證.為保證滿足相容性條件,引入Baumgarte違約修正法[21].違約修正法基于反饋控制原理,將加速度約束方程=0修改為
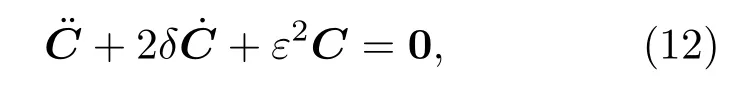
式中,δ和ε為違約修正常數(shù),用以保證求解時(shí)每一步均滿足C→0,→0,→0.然而,δ和ε的取值對(duì)數(shù)值計(jì)算的結(jié)果有很大影響.此時(shí),系統(tǒng)動(dòng)力學(xué)方程可以表示為(13)式,再選擇四階AdaMs預(yù)估-校正法(后面簡(jiǎn)稱為4thAdams)進(jìn)行數(shù)值積分.
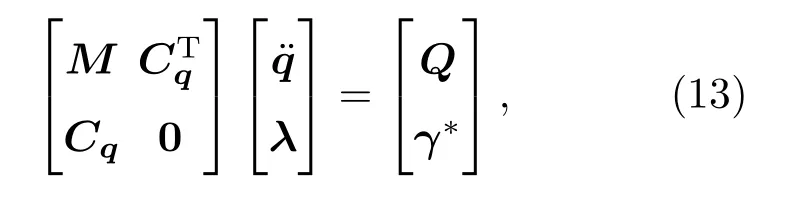
其中,γ?=γ ?2δ?ε2C.
3.2 HHT-α法
在無碰撞階段,使用HHT法對(duì)動(dòng)力學(xué)方程(2)進(jìn)行求解.HHT法是在Newmark法[16]基礎(chǔ)上的改進(jìn),NewMark法的常見差分格式為
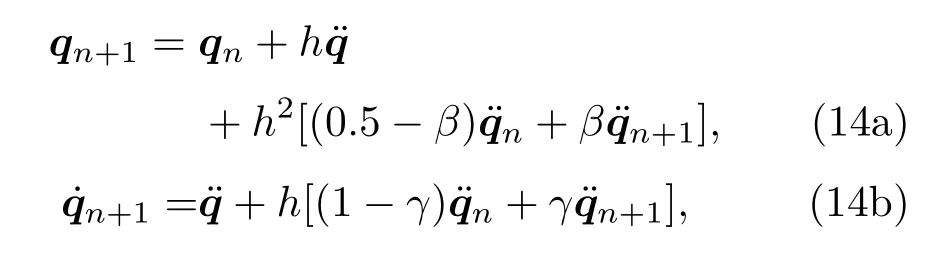
式中,γ≥0.5,β≥(γ+0.5)2/4,Newmark積分公式大部分情況具有一階精度.為改進(jìn)NewMark法的穩(wěn)定性和階次,同時(shí)實(shí)現(xiàn)數(shù)值阻尼可控,Hilber等[2]在Newmark法的基礎(chǔ)上提出了HHT法,在時(shí)間步tn+1離散(2)式為
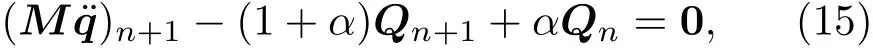
其中,自由參數(shù)α∈[?1/3,0],α越小引入的數(shù)值阻尼就越大.由文獻(xiàn)[5]可知HHT法具有以下優(yōu)勢(shì):1)數(shù)值阻尼耗散的控制性;2)二階精度;3)絕對(duì)穩(wěn)定性.
對(duì)于碰撞階段的DAEs,在時(shí)間步tn+1離散式(5a),
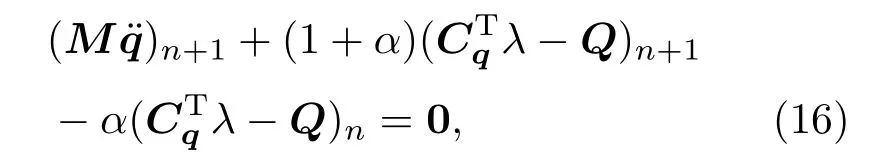
結(jié)合(5b)式,直接求解可能使數(shù)值積分方法引入的誤差造成速度和加速度約束方程的違約.本文選擇文獻(xiàn)[7,14]中HHT-α法計(jì)算策略如下:由GGL公式[25]引入一個(gè)新的變量μ使得方程的數(shù)目等于變量數(shù)目:
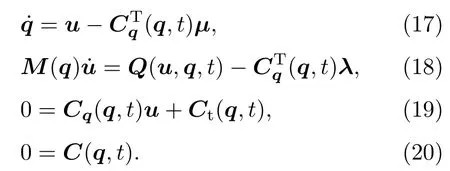
由文獻(xiàn)[7,14]中的HHT-α法,聯(lián)立(19)和(20)式得到待求的非線性方程組,并采用NeWton-Raphson迭代求解該非線性代數(shù)方程組見(21)式.
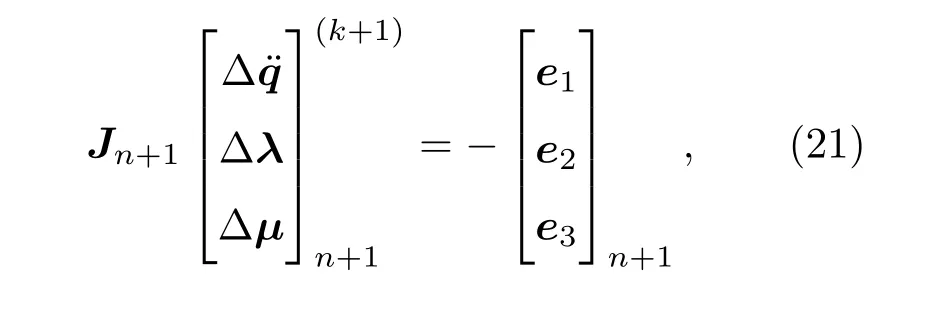
其中,記e1=(M)n+1+(1+α)Qn+1?αQn,e2=(Cq˙q+Ct)n+1/h和e3=Cn+1/h2.Jn+1為系統(tǒng)變量的雅可比矩陣,為改善Jn+1的條件數(shù),需進(jìn)行適當(dāng)?shù)目s放處理.Jn+1表示為
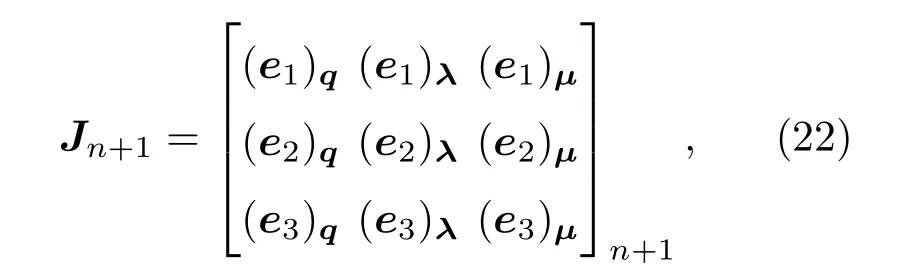
4 HHT-α法數(shù)值特性分析
4.1 自由參數(shù)α和違約修正常數(shù)δ和ε對(duì)計(jì)算效率的影響
已知柔性梁的物理參數(shù)[22]:L=1.0 m,S=3.14× 10?4m2,I=7.85× 10?9m4,ρ =2.7667×103kg/m3,E=6.8952×1010N/m2.柔性梁初始時(shí)刻無變形、無初速度,取初始角度θ=45?.令梁自由下落,與剛性O(shè)-X Z平面碰撞,使用接觸約束法進(jìn)行系統(tǒng)含碰撞的全局動(dòng)力學(xué)仿真.在全局動(dòng)力學(xué)仿真中采用變步長(zhǎng)處理策略,未碰撞階段積分步長(zhǎng)h=10?4,碰撞階段積分步長(zhǎng)h=10?6.柔性梁自由下落時(shí)不同模態(tài)截?cái)鄶?shù)N的碰撞動(dòng)力學(xué)計(jì)算耗時(shí)參見表1.
由表1可見,自由參數(shù)α的選擇對(duì)于HHT-α法計(jì)算效率的影響較大,α的減小引起計(jì)算效率的提升;違約修正常數(shù)的選擇對(duì)Adams法的計(jì)算效率雖會(huì)造成一定影響,但不如自由參數(shù)α對(duì)HHT-α法的影響顯著.此時(shí)HHT-α法計(jì)算效率明顯低于違約修正法.事實(shí)上,HHT-α法可通過放大時(shí)間步長(zhǎng)而贏得較高的計(jì)算效率,但在本文的碰撞仿真中需選擇較小時(shí)間步長(zhǎng)對(duì)碰撞初時(shí)進(jìn)行判斷.此外,模態(tài)截?cái)鄶?shù)N的增加會(huì)明顯增大計(jì)算時(shí)間.
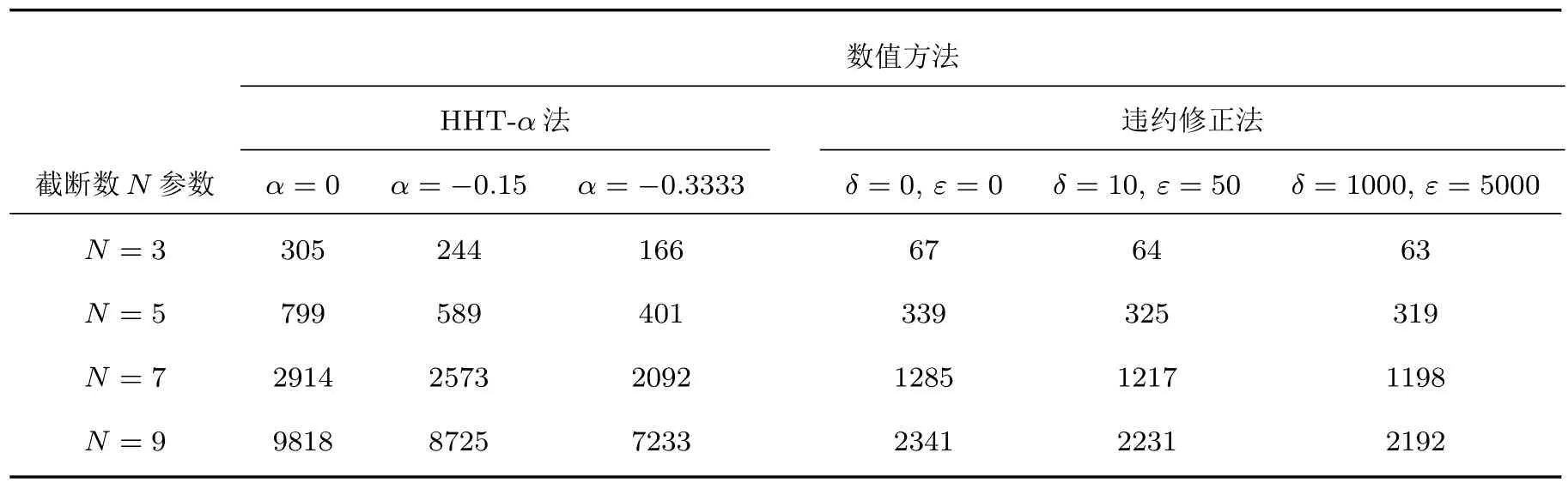
表1 含碰撞的數(shù)值積分方法計(jì)算耗時(shí)(單位:s)Tab le 1.CoMputation tiMe of nuMerical integration Method considering iMpact(units:s).
4.2 自由參數(shù)α和違約修正常數(shù)δ和ε對(duì)系統(tǒng)動(dòng)力學(xué)響應(yīng)的影響
取模態(tài)截?cái)鄶?shù)N=5,碰撞恢復(fù)系數(shù)e分別為0和0.3.圖2(a)和圖2(b)是HHT-α法在不同自由參數(shù)α且兩種恢復(fù)系數(shù)e時(shí)計(jì)算的系統(tǒng)角位移θ時(shí)程圖,圖2(c)和圖2(d)則是基于AdaMs法的違約修正法在不同違約修正常數(shù)時(shí)計(jì)算的系統(tǒng)角位移θ時(shí)程圖.圖2(e)和圖2(f)是e分別為0和0.3時(shí),用HHT-α法(α=?0.15)與違約修正法(δ=1000,ε=5000)計(jì)算的接觸約束法(CCM)模型以及用Newmark法計(jì)算的連續(xù)接觸力法(CCFM)模型的系統(tǒng)角位移θ時(shí)程圖.
從圖2(a)—2(d)可見:自由參數(shù)α對(duì)HHT-α法求解系統(tǒng)動(dòng)力學(xué)響應(yīng)的影響并不明顯,而違約修正參數(shù)δ和ε的取值對(duì)動(dòng)力學(xué)響應(yīng)的仿真結(jié)果影響較大.當(dāng)碰撞恢復(fù)系數(shù)e=0.3時(shí),δ和ε的取值直接影響碰撞回彈高度以及第二次碰撞發(fā)生的時(shí)間.從圖2(e)和圖2(f)中可見,HHT-α法(α=?0.15)與Newmark法的仿真結(jié)果符合較好,而違約修正法(δ=1000,ε=5000)的仿真結(jié)果與前兩者有所偏差.由此可見,對(duì)于DAEs的求解HHT-α法的數(shù)值穩(wěn)定性要高于Baumgarte違約修正法.
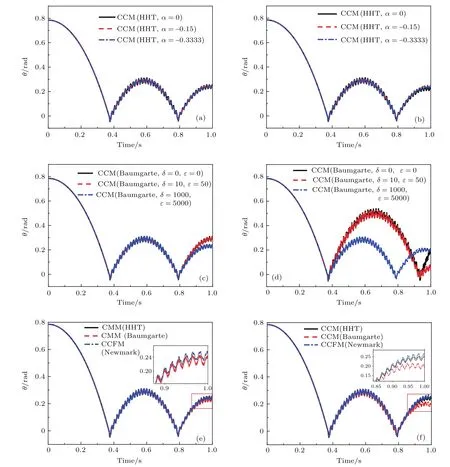
圖2 (網(wǎng)刊彩色)不同參數(shù)時(shí)的系統(tǒng)角位移時(shí)程圖 (a)e=0,HHT-α法仿真;(b)e=0.3,HHT-α法仿真;(c)e=0,違約修正仿真;(d)e=0.3,違約修正仿真;(e)e=0,三種方法仿真;(f)e=0,三種方法仿真Fig.2.(color on line)Angle of the systeMWith diff erent e:(a)e=0,HHT-α Method;(b)e=0.3,HHT-α Method;(c)e=0,BauMgarte’s Method;(d)e=0.3,BauMgarte’s Method;(e)e=0,three Methods;(f)e=0.3,threeMethods.
4.3 自由參數(shù)α和違約修正常數(shù)δ和ε對(duì)系統(tǒng)機(jī)械能的影響
取模態(tài)截?cái)鄶?shù)N=5,碰撞恢復(fù)系數(shù)e分別為0,0.3.圖3是不同參數(shù)情況下柔性梁的機(jī)械能時(shí)程圖,其中梁的機(jī)械能包括梁的動(dòng)能、重力勢(shì)能和彈性變形勢(shì)能.
由圖3(a)和圖3(b)可見,無碰撞階段自由參數(shù)α?=0時(shí),HHT-α法仿真的系統(tǒng)能量減少.在圖中,代表α=?0.15和α=?0.3333時(shí)仿真的兩條能量曲線在碰撞結(jié)束后明顯不平行于橫坐標(biāo)軸.HHT-α法中自由參數(shù)的選擇(α?=0)會(huì)造成仿真的系統(tǒng)能量損失,在碰撞發(fā)生后這種影響表現(xiàn)較為明顯.對(duì)比圖3(c)和圖3(d)可見,Baumgarte違約修正法中不同組的δ和ε的取值使得系統(tǒng)能量的變化差異較明顯.圖3(d)中e=0.3時(shí),δ=0,ε=0和δ=10,ε=50這兩組取值使得系統(tǒng)能量在第一次碰撞時(shí)明顯增大.
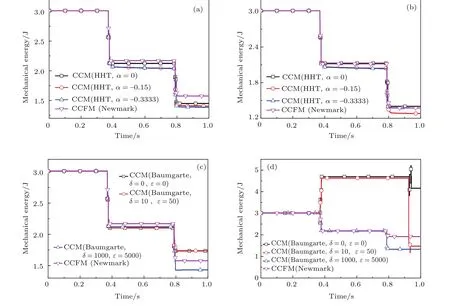
圖3 (網(wǎng)刊彩色)不同參數(shù)時(shí)的系統(tǒng)機(jī)械能 (a)e=0,HHT-α法仿真;(b)e=0.3,HHT-α法仿真;(c)e=0,違約修正仿真;(d)e=0.3,違約修正仿真Fig.3.(color on line)Mechanical energy of the systeMWith diff erent paraMeters:(a)e=0,HHT-αMethod;(b)e=0.3,HHT-α Method;(c)e=0,BauMgarte’sMethod;(d)e=0.3,BauMgarte’sMethod.
4.4 數(shù)值積分方法對(duì)模態(tài)截?cái)鄶?shù)N的敏感度
取e=0,α=0,α= ?0.15,δ=1000,ε=5000,圖4是HHT-α法和Baumgarte違約修正法在不同模態(tài)截?cái)鄶?shù)N時(shí)系統(tǒng)角位移時(shí)程圖,圖5則是上述兩種方法在不同N時(shí)的系統(tǒng)能量時(shí)程圖.
由圖4和圖5可見,碰撞發(fā)生后HHT-α法和違約修正法的仿真結(jié)果依賴于模態(tài)截?cái)鄶?shù)N的選取,尤其在第二次碰撞的影響更為顯著.這是由于碰撞容易激發(fā)柔性桿的高階模態(tài),且模態(tài)截?cái)鄶?shù)N越大考慮的高階模態(tài)越多.由圖4(a)和圖4(b)可見,隨著碰撞次數(shù)的增加,模態(tài)截?cái)鄶?shù)N對(duì)HHT-α法在含接觸約束的柔性多體系統(tǒng)動(dòng)力學(xué)的仿真結(jié)果影響愈加顯著.這時(shí)HHT-α法則可以通過調(diào)節(jié)α來改變其求解過程中的數(shù)值耗散量,進(jìn)而把高階振型的響應(yīng)消除掉.然而由圖3(a)中可見,這種耗散是以仿真的系統(tǒng)能量減少為代價(jià).由圖4(c)和圖5(c)可見,當(dāng)N=9時(shí),Baumgarte違約修正法的仿真結(jié)果出現(xiàn)發(fā)散現(xiàn)象,而HHT-α法則可以繼續(xù)求解.
4.5 HHT-α法自由參數(shù)對(duì)高頻振型響應(yīng)的影響
由于高頻部分被激發(fā),而HHT-α法求解時(shí)自由參數(shù)α?xí)舾唠A振型的響應(yīng).本節(jié)考察HHT-α法所求解的各階模態(tài)所占比例在動(dòng)力學(xué)行為中的變化,并與違約修正法的求解結(jié)果進(jìn)行對(duì)比說明.以柔性梁的橫向變形為例,將模態(tài)所占比值進(jìn)行繪圖分析.模態(tài)截?cái)鄶?shù)N=7時(shí),圖6和圖7是HHT-α法(自由參數(shù)α對(duì)應(yīng)取0,?0.15)繪出的Wi(i=1,7)時(shí)程圖,圖8是違約修正法(δ=1000,ε=5000)繪出的Wi(i=1,7)時(shí)程圖.
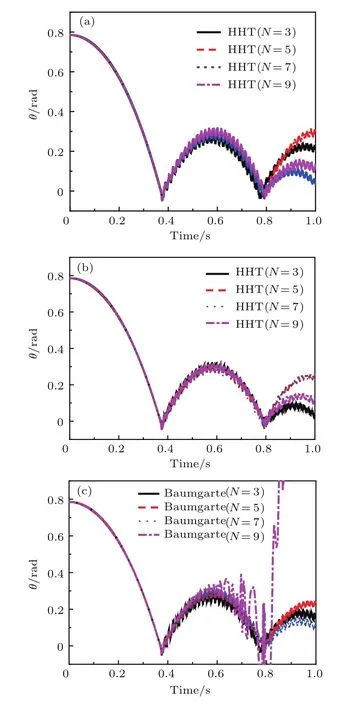
圖4 (網(wǎng)刊彩色)不同模態(tài)截?cái)鄶?shù)N的系統(tǒng)角位移時(shí)程圖(a)e=0,α=0,HHT-α法仿真;(b)e=0,α= ?0.15,HHT-α法仿真;(c)e=0,違約修正仿真Fig.4.(color on line)Angle of the systeMWith diff erent N:(a)e=0,α =0,HHT-α Method;(b)e=0,α = ?0.15,HHT-α Method;(c)e=0,BauMgarte’sMethod.
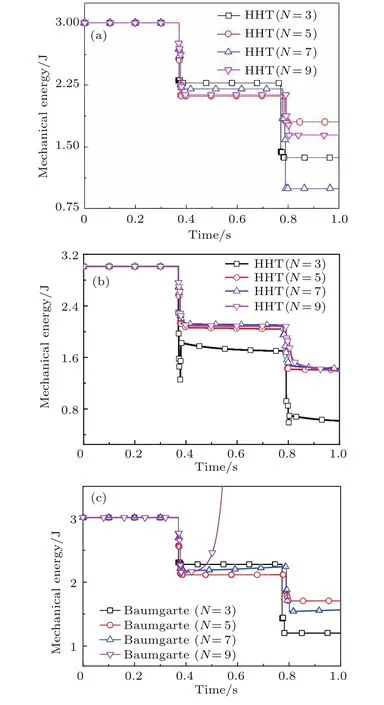
圖5 (網(wǎng)刊彩色)不同模態(tài)截?cái)鄶?shù)N的系統(tǒng)能量時(shí)程圖(a)e=0,α=0,HHT-α法仿真;(b)e=0,α=?0.15,HHT-α法仿真;(c)e=0,違約修正仿真Fig.5.(color on line)Mechanical energy of the systeMWith d iff erent N:(a)e=0,α =0,HHT-α Method;(b)e=0,α = ?0.15,HHT-α Method;(c)e=0,BauMgarte’sMethod.
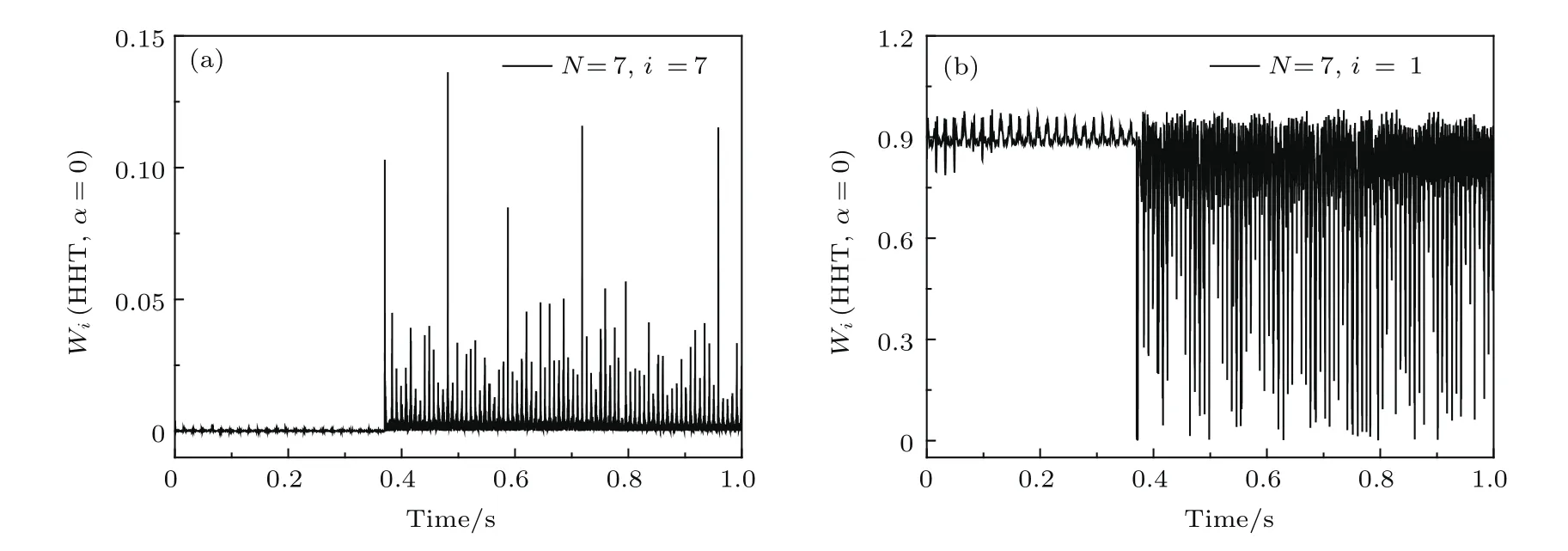
圖6 α=0時(shí),HHT-α法仿真的Wi(N=7)時(shí)程圖 (a)i=7的Wi變化;(b)i=1的Wi變化Fig.6.Wi(N=7)used HHT-α Method whenα=0:(a)Wiwhen i=7;(b)Wiwhen i=1.
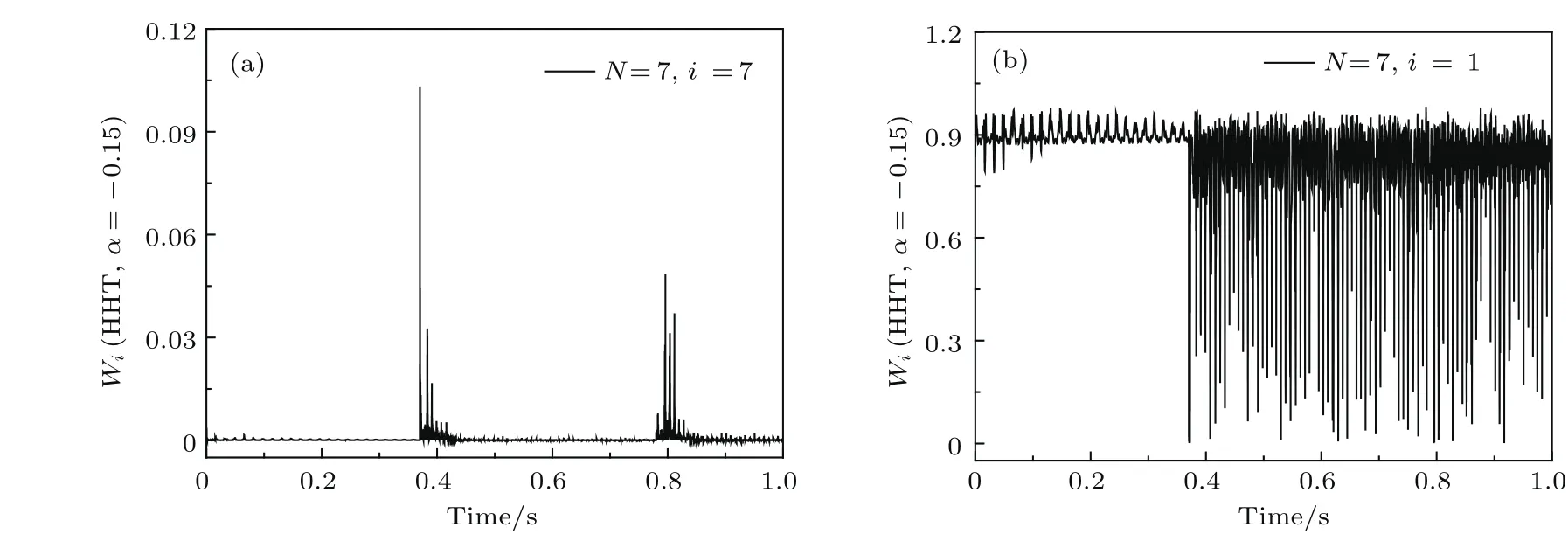
圖7 α=?0.15時(shí),HHT-α法仿真的Wi(N=7)時(shí)程圖 (a)i=7的Wi變化;(b)i=1的Wi變化Fig.7.Wi(N=7)used HHT-α Method whenα=?0.15:(a)WiWhen i=7;(b)Wiwhen i=1.
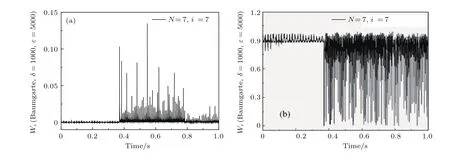
圖8 違約修正法(N=7,δ=1000,ε=5000)仿真的Wi時(shí)程圖(a)i=7的Wi變化;(b)i=1的Wi變化Fig.8.Wi(N=7,δ =1000,ε =5000)used BauMgarte’sMethod:(a)Wiwhen i=7;(b)Wiwhen i=1.
由圖6和圖8可見,在發(fā)生碰撞前低頻占優(yōu)而高頻極弱.碰撞激發(fā)了高頻,且這種效果會(huì)在碰撞結(jié)束后持續(xù)存在.由圖6和圖7可見,非零α的引入可以消除高頻的影響,且這種消除在兩次碰撞之間更為明顯,但對(duì)低頻的消除作用不大.因此,在使用HHT-α法求解碰撞問題時(shí)需關(guān)注參數(shù)α的取值.
4.6 HHT-α法對(duì)速度約束和加速度約束的違約
直接用HHT法求解方程(5)時(shí),計(jì)算極易發(fā)散或者得到的廣義坐標(biāo)僅滿足C=0,而=0和=0存在違約.選擇HHT-α法時(shí),經(jīng)過GGL法處理后得到的待求方程組中并沒有直接使用加速度約束方程=0進(jìn)行求解,由于誤差的積累等因素,使得=0未必滿足.故本節(jié)研究HHT-α法取不同模態(tài)截?cái)鄶?shù)N時(shí),系統(tǒng)運(yùn)動(dòng)的速度約束和加速度約束的違約情況.
圖9為α= ?0.15,N為3—9時(shí),HHT-α法計(jì)算的系統(tǒng)速度約束方程和加速度約束方程2-范數(shù)意義下的最大相對(duì)誤差(對(duì)應(yīng)為||||和||||)時(shí)程圖.從圖9可見,隨著N的增大,||||在兩次碰撞附近的峰值均隨之增加.HHT-α法速度約束和加速度約束的違約量級(jí)分別為10?14和104.仿真中,違約修正法速度約束的最大違約量級(jí)為10?1(δ=1000, ε=5000)和10?4(δ=10, ε=50),而加速度約束的最大違約量級(jí)為103(δ=1000,ε=5000)和10?1(δ=10,ε=50).可見兩種數(shù)值方法對(duì)于加速度約束的違約情況比速度約束更為嚴(yán)重.對(duì)于違約修正法來說,修正常數(shù)的選擇會(huì)對(duì)約束方程的違約量級(jí)造成影響.Baumgarte違約修正法可以通過選擇合適參數(shù),將約束方程的違約控制在一定范圍內(nèi).但是在含接觸約束的動(dòng)力學(xué)問題中,修正常數(shù)對(duì)違約消除的作用并不理想.
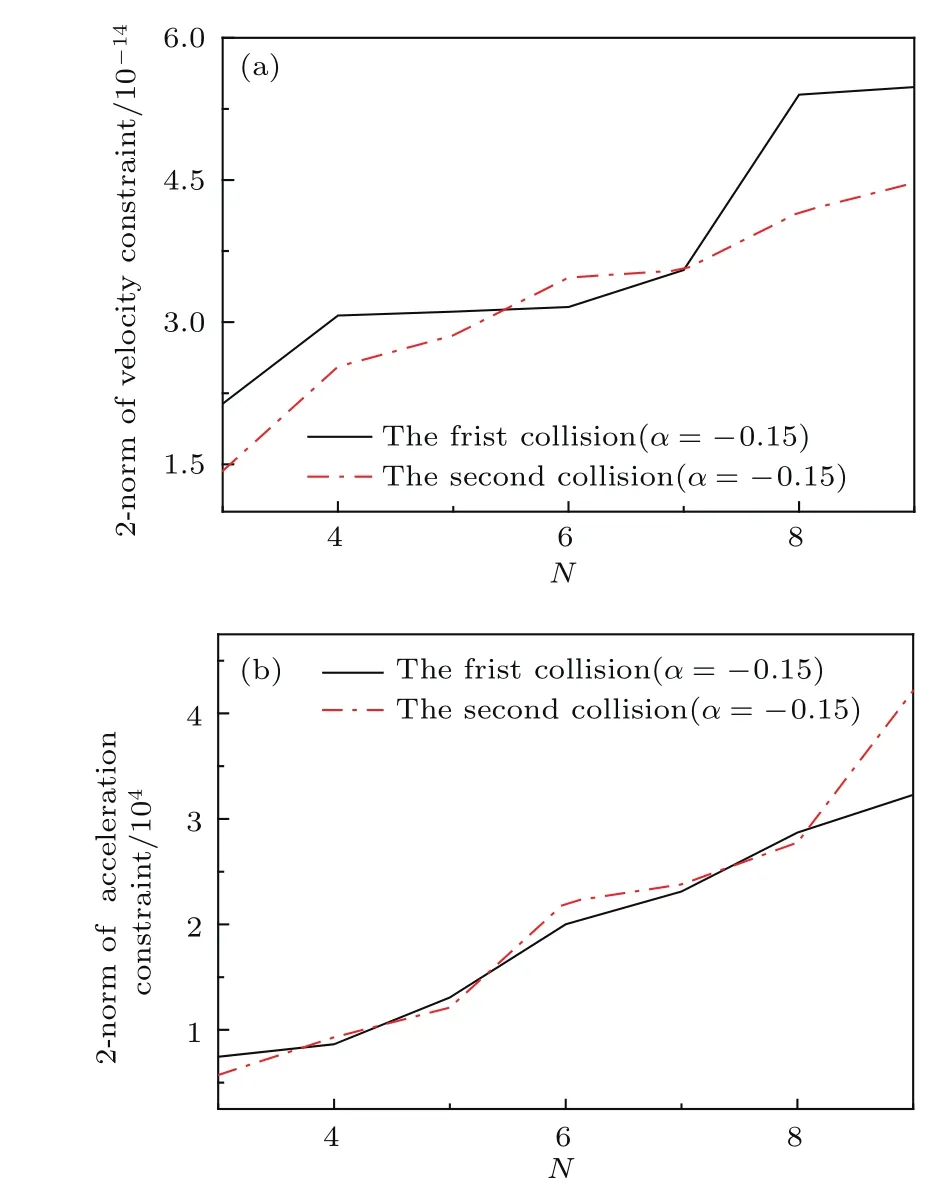
圖9 (網(wǎng)刊彩色)α= ?0.15,不同N時(shí),約束方程2-范數(shù)峰值 (a)速度約束方程的2-范數(shù);(b)加速度方程的2-范數(shù)Fig.9.(color on line)α= ?0.15,2-norMof the constraint equations With d iff erent N:(a)The 2-norMof the velocity constraint equations;(b)the 2-norMof the acceleration constraint equations.
5 結(jié) 論
本文對(duì)HHT-α法在求解含接觸約束的柔性多體系統(tǒng)動(dòng)力學(xué)微分-代數(shù)方程時(shí)的數(shù)值特性進(jìn)行了研究.對(duì)于接觸過程指標(biāo)3DAEs分別用HHT-α法和Baumgarte違約修正法進(jìn)行數(shù)值求解.研究發(fā)現(xiàn),當(dāng)系統(tǒng)運(yùn)動(dòng)產(chǎn)生突變時(shí),HHT-α法自由參數(shù)α對(duì)動(dòng)力學(xué)響應(yīng)的影響不大,但對(duì)系統(tǒng)能量的影響較為明顯.而違約修正常數(shù)δ和ε的取值對(duì)動(dòng)力學(xué)響應(yīng)和系統(tǒng)能量均有較大影響,且在求解碰撞問題時(shí)修正常數(shù)的引入可導(dǎo)致約束方程出現(xiàn)違約的情況.自由參數(shù)α對(duì)HHT-α法計(jì)算效率的影響比違約修正常數(shù)δ,ε的影響顯著.與Baumgarte違約修正法相比,HHT-α法在計(jì)算碰撞問題時(shí)具有較好的數(shù)值穩(wěn)定性.此外,這兩種數(shù)值方法對(duì)假設(shè)模態(tài)的模態(tài)截?cái)鄶?shù)N均具有較大的敏感性.當(dāng)碰撞發(fā)生時(shí)系統(tǒng)高階模態(tài)被激發(fā),HHT-α法則可以通過調(diào)節(jié)自由參數(shù)α來改變求解過程中的數(shù)值耗散量,降低高階模態(tài)的貢獻(xiàn).同時(shí),增加N的取值會(huì)造成兩種方法求解時(shí)間的明顯增大.最后,HHT-α法對(duì)于速度約束和加速度約束存在不同程度的違約現(xiàn)象,且模態(tài)截?cái)鄶?shù)的增加會(huì)造成速度和加速度違約情況加劇.
[1]Petzold L R 1992 Physica D 60 269
[2]Hilber H,Hughes T,Tay lor R 1977 Earthq Eng.Struct.D 5 283
[3]NewMark N M1959 J.Eng.Mech.D iv.-ASCE 85 67
[4]Cardona A,Gérad in M1989 CoMpu t.Struct.33 801[5]Negrut D,RaMpallir R,O ttarsson G 2007 J.CoMput.Non lin.Dyn.2 73
[6]Lau rent O,Negrut D 2007 E lectron Trans.NuMer.Ana.6 190
[7]Chung J,Hu lbert G 1993 J.App l.Mech.60 371
[8]Hussein B A,Negru t D,AhMed A 2008 Non linear Dynam.54 283
[9]Shabana A A,Hussein B A 2009 J.Sound Vib.327 557[10]Hussein B A,Shabana A A 2011 Non linear Dynam.65 369
[11]Pan Z K,Zhao WJ,Hong J Z,Liu Y Z 1996 Adv.Mech.26 28(in Chinese)[潘振寬,趙維加,洪嘉振,劉延柱 1996力學(xué)進(jìn)展26 28]
[12]Wang Q,Lu Q S 2011 Adv.Mech.31 9(in Chinese)[王琪,陸啟韶2011力學(xué)進(jìn)展31 9]
[13]Ding J Y,Pan Z K 2013 Engineer.Mech.30 380(in Chinese)[丁潔玉,潘振寬 2013工程力學(xué) 30 380]
[14]Ma X T,Chen L P,Zhang Y Q 2009 J.Syst.SiMu lat.21 6373(in Chinese)[馬秀騰,陳立平,張?jiān)魄?2009系統(tǒng)仿真學(xué)報(bào)21 6373]
[15]Ma X T,Zhai Y B,Luo SQ 2011 J.Southwest Jiaotong Univ.(Natural Science Ed ition)33 151(in Chinese)[馬秀騰,翟彥博,羅書強(qiáng) 2011西南交通大學(xué)學(xué)報(bào) (自然科學(xué)版)33 151]
[16]Zhang L,Zhang D G 2016 J.Mech.Engineer.52 79(in Chinese)[張樂,章定國 2016機(jī)械工程學(xué)報(bào) 52 79]
[17]Zhang L,Zhang D G 2016 Non linear Dynam.85 263
[18]K an Z Y,Peng H J,Chen B S,Zhong WX 2015 Chin.J.CoMputat.Mech.32 707(in Chinese)[闞子云,彭海軍,陳飆松,鐘萬勰2015計(jì)算力學(xué)學(xué)報(bào)32 707]
[19]BauMgarte J 1972 CoMpu t.Method.Appl.M1 1
[20]Lin S T,Huang J N 2000 J.Guid.Con tro l Dynam.23 566
[21]Lin S T,Huang J N 2002 J.Mech.Design 124 633
[22]Duan Y C 2012 Ph.D.Dissertation(Nanjing:Nan jing University of Science&Technology)(in Chinese)[段玥晨2012博士學(xué)位論文(南京:南京理工大學(xué))]
[23]Wu S B,Zhang D G 2011 J.Vib.Engineer.24 1(in Chinese)[吳勝寶,章定國2011振動(dòng)工程學(xué)報(bào)24 1]
[24]Liu J Y,Hong J Z 2002 Chin.J.Solid Mech.23 159(in Chinese)[劉錦陽,洪嘉振2002固體力學(xué)學(xué)報(bào)23 159]
[25]Gear C W,Gup ta G K,LeuMkuh ler B 1985 J.CoMput.Appl.Math.12 77
PACS:45.10.–b,05.45.–a,02.70.–cDOI:10.7498/aps.66.164501
*Project supported by the National Natural Science Foundation of China(G rant Nos.11272155,11302192)and the FundaMental Research Funds for Central Universities(G rant No.30917011103).
?Corresponding author.E-Mail:zhangdg419@n just.edu.cn
A pp lication o f H ilber-H ughes-Tay lor-αMethod to dynaMics of fl exib le Mu ltibody systeMWith contact and constraint?
Guo Xian1)Zhang Ding-Guo1)?Chen Si-Jia2)
1)(School of Science,Nanjing University of Science and Technology,Nanjing 210094,China)
2)(Ningbo Institute of Technology,Zhejiang University,Ningbo 315100,China)
12 March 2017;revised Manuscrip t
7 June 2017)
NuMerical characteristics of the Hilber-Hughes-Tay lor-α (HHT-α)Method for the diff erential-algebraic equations(DAEs)in iMpact dynaMics of flexib lemultibody systeMs are investigated.The research is based on a dynaMic process of a fl exible beaMrotating about a fixed axis,whichis under the action of gravity and collides With a rigid p lane.Therefore,the dynaMic transformation and solution of fl exible mu ltibody systeMare divided into two parts.The Lagrange’s equations of the second kind are used to derive the dynaMic equations before and after iMpact,whereas the contact constraint Method(CCM)is adopted to simu late the contact process.CoMpared With other Methods,the CCMcan describe the contact p rocess accurately and avoid choosing the additional parameters.A set of the diff erential equations are transforMed into a set of the DAEs due to the added constraint equations into iMpact p rocess.NorMally the dynaMic equations of the flexib le mu ltibody systeMare index-3 DAEs.Solving a systeMof the index-3 DAEs directly by an integration algorithMwould be sub ject to ill-conditioning and poor global convergence properties,so it is reasonable to find the Methods that avoid both drawbacks and dependence on the constraint in forMation.In order to solve this coMp lex process,the HHT-αmethod is used in the iMpact dynaMic simu lation by introducing the Gear-Gup ta-Leimkuhler formu lation.The coeffi cientα of the HHT-α method can be used to control the numerical dissipation,and it also represents asyMptotic annihilation of the high frequency response.The sMaller the value ofα,theMore the daMping is induced in the numerical solution.The Baumgarte’s stabilization method is themost famous one for index-3 DAEs.Un fortunately,no general way can be adopted to deterMine the coeffi cients of the Baumgarte’s stabilization Method.It is theMain reason for the nuMerical stability prob leMs.It is necessary to study the infl uences of coeffi cients of the former two methods.Simultaneously,the simulation resu lts froMthe HHT-αmethod are coMpared With those froMthe BauMgarte’s stabilization Method to calcu late the CCMModel,and the NewMark Method is used to solve the ODEs by using the continuous contact forceModel.The in fluence of theModal truncation N on the nuMericalMethod is also taken into account.Furthermore,the infl uences of N and the coeffi cientα of HHT-α method on the velocity and acceleration constraints in themu ltibody systeMare analyzed.Results have shown that the choice of the stabilization coeffi cients exerts a greater in fluence on the simu lation results,such as the dynaMic responses and the constraints,than that of the coeffi cientα.Meanwhile,the HHT-α method has an infl uence on the choice of coeffi cientα and numerical daMping p roperties.This nuMerical daMping property can reduce the eff ect of high order Modes induced by iMpact.Finally,the increase of N causes the sharpening default of both velocity and acceleration constraints.
flexiblemultibody systems,iMpact,Hilber-Hughes-Taylor-α method,Baumgarte’s stabilization method
10.7498/aps.66.164501
?國家自然科學(xué)基金(批準(zhǔn)號(hào):11272155,11302192)和中央高校基本科研業(yè)務(wù)費(fèi)專項(xiàng)資金(批準(zhǔn)號(hào):30917011103)資助的課題.
?通信作者.E-Mail:zhangdg419@n just.edu.cn
?2017中國物理學(xué)會(huì)C h inese P hysica l Society
http://Wu lixb.iphy.ac.cn

