外差式偏振干涉成像光譜技術研究?

才啟勝黃旻 韓煒 叢麟驍2) 路向寧

1)(中國科學院光電研究院,計算光學成像技術重點實驗室,北京 100094)

2)(中國科學院大學,北京 100049)

外差式偏振干涉成像光譜技術研究?

才啟勝1)?黃旻1)韓煒1)叢麟驍1)2)路向寧1)

1)(中國科學院光電研究院,計算光學成像技術重點實驗室,北京 100094)

2)(中國科學院大學,北京 100049)

(2017年3月15日收到;2017年5月4日收到修改稿)

提出了一種新型的基于Savart偏光鏡的外差式偏振干涉成像光譜技術,該技術在偏振干涉成像光譜儀中引入一對平行偏振光柵對,使其得到的干涉圖頻率與波數相關,具有了波數外差的特點,降低了干涉圖頻率,從而可利用較少的采樣點數實現很高的光譜分辨率.對外差式偏振干涉成像光譜技術的基本原理進行了研究,詳細分析了系統光程差、干涉圖表達式、光譜分辨率以及光譜復原方法等.最后給出了外差式偏振干涉成像光譜儀的設計實例并進行了計算機仿真模擬,所復原的光譜與輸入光譜曲線相符合,驗證了方案的正確性.外差式偏振干涉成像光譜儀具有結構緊湊、光通量高、穩定性強、光譜分辨率高的特點,尤其適合超小型高穩定性、高探測靈敏度的高光譜探測應用.

傅里葉變換光譜技術,干涉,偏振,空間外差

1 引 言

偏振干涉成像光譜技術是以雙折射晶體為分光元件的一種干涉成像光譜技術.從20世紀90年代初開始,偏振干涉光譜儀得到廣泛的研究.典型的偏振干涉光譜儀如:日本大阪大學1992年研制的基于Savart偏光鏡的多通道干涉光譜儀[1],英國圣安德魯斯大學1996年研制的基于Wollaston偏光鏡的具有補償功能的偏振干涉光譜儀[2?4].1996年,美國華盛頓大學研制出了數字陣列掃描干涉成像光譜儀DASI[5],DASI是一種利用Wollaston棱鏡分光的空間調制偏振干涉成像光譜儀,其與變形的Sagnac干涉成像光譜儀原理相似[6],系統中都存在一個狹縫.由于狹縫的存在,使得進入系統的光通量大大降低,為了克服狹縫式偏振干涉成像光譜儀的缺點,2002年,張淳民等[7,8]提出了一種基于Savart偏光鏡的穩態偏振干涉成像光譜儀SPIIS.SPIIS是一種點到點的完全成像系統,其直接得到的是疊加了干涉條紋的目標二維圖像,通過推掃成像獲取目標的完整干涉圖,由于系統中不存在狹縫,使得其具有很高的光通量[9],另外,該光譜儀還具有超小型、高穩定性等優點.

空間外差光譜技術是20世紀90年代逐漸發展起來的一種具有超高光譜分辨率的干涉光譜技術,該技術通過在干涉儀中加入特定的光學元件降低干涉圖的空間頻率,從而以較少的采樣點數實現很高的光譜分辨率.1971年,日本大阪大學的Dohi和Suzuki[10]首先提出了空間外差光譜技術的概念.1990年美國威斯康星大學的Roesler與Harlander采用電荷耦合探測器進行了實用型空間外差光譜儀的實驗研究[11].其原理是用光柵代替Michelson干涉儀中的兩個平面反射鏡,使干涉圖產生外差的效果.隨后,他們在美國海軍研究實驗室和NASA的支持下開始了中層大氣自由基空間外差成像儀SHIMMER系統的研制[12,13].兩代SHIMMER系統分別于2002年10月和2007年3月試飛成功,得到的實驗數據與理論符合.由于空間外差光譜技術超高光譜分辨率的特點,相繼提出了多種形式的空間外差成像光譜儀,如基于Mach-Zehnder干涉儀的空間外差光譜儀MZ-SHS[14],基于Sagnac干涉儀的大孔徑空間外差干涉成像光譜儀LASHIS[15],以及基于Wollaston偏光鏡的偏振空間外差光譜儀PSHI[16].

本文在穩態偏振干涉成像光譜儀SPIIS的基礎上提出一種外差式偏振干涉成像光譜儀(heterodyne polarization interference imaging spectrometer,HPIIS),該光譜儀的成像方式與SPIIS相似,繼承了SPIIS的高光通量、高穩定性等優點,并利用干涉圖外差技術降低干涉圖頻率,通過較少的采樣點數實現高光譜分辨率探測.另外,HPIIS與同樣采用了外差技術的偏振空間外差光譜儀PSHI相比具有高光通量優點:PSHI是基于角剪切的Wollaston偏光鏡,且系統存在狹縫,是點到面的成像系統;而HPIIS是基于橫向剪切的Savart偏光鏡,系統中無狹縫,是點到點的完全成像系統,具有更高的光通量.本文對HPIIS的基本原理進行了詳細闡述,并給出了設計實例,對系統進行干涉圖仿真與光譜復原.

2 理論分析

2.1 基本原理

外差式偏振干涉成像光譜儀HPIIS的原理如圖1所示,其在SPIIS的基礎上引入一對偏振光柵來實現波數外差.HPIIS主要由前置鏡L0、準直鏡L1、起偏器P、Savart偏光鏡、1/4波片QWP、偏振光柵對PG 1和PG2[17,18]、檢偏器A、成像鏡L2、面陣探測器D以及數據處理系統組成.前置鏡L0將探測目標成像在視場光闌處,視場光闌位于準直鏡L1的前焦面上,目標上某一點發出的光經過L0和L1后變為平行光入射到起偏器P上,起偏器P的偏振方向在XY平面內且與X和Y軸正向成45?,光線經過起偏器P后變為線偏振光進入Savart偏光鏡,Savart偏光鏡由兩塊厚度為t的單軸晶體組成,第一塊晶體的光軸在X Z平面內且與X和Z軸正向成45?;第二塊晶體的光軸在YZ平面內且與Y和Z軸正向成45?.這樣,光線進入Savart偏光鏡的第一塊晶體后分為尋常光(o光)和非尋常光(e光),o光沿原方向傳播,e光發生偏折,之后分開的兩束光入射到第二塊晶體,原o光變為e光產生偏折,再經過Savart偏光鏡的后表面偏折后平行于入射方向射出(oe光).同理,原e光變為o光偏折后平行于入射方向射出(eo光).因此,光線經過Savart偏光鏡后變為振動方向互相垂直的平行于入射方向且具有一定間距(橫向剪切量)的兩束線偏振光.這兩束振動方向互相垂直的線偏振光經過1/4波片QWP后變為兩束旋轉方向相反的圓偏振光,然后入射到平行偏振光柵對(PG 1和PG2)中.右旋偏振光和左旋偏振光經過PG1后分別產生+1級衍射和?1級衍射[16],不同波長的入射光其衍射角不同,如圖1中所示,紅色虛線所表示的光線的衍射角大于藍色實線所表示的光線的衍射角.偏振光柵PG2的刻線密度與PG1相同,且刻線方向和刻線平面均與PG1平行,由于這對平行光柵的作用,光線經過PG2衍射后,其出射方向與入射PG1時的方向相同,即具有一定剪切量的兩束光經過平行光柵對后仍為平行光束,只是其橫向剪切量產生了變化,且剪切量與波數相關.隨后,兩束光經過檢偏器A后變為相干光.探測器D位于成像L2的后焦面上,兩束平行相干光束經過L2后在探測器上相干疊加,不同的目標點成像在探測器的不同位置處,最終得到疊加了干涉信息的目標圖像,經過后續數據處理后,即可復原出目標的光譜信息.

圖1 (網刊彩色)外差式偏振干涉成像光譜儀原理圖Fig.1.(color on line)ScheMatic of the heterodyne polarization interference iMaging spectroMeter.

2.2 干涉圖計算

系統得到的干涉圖與兩束光的橫向剪切量有關,系統的等效光路圖如圖2所示,Savart偏光鏡與平行光柵對將探測目標分為兩個虛像,兩虛像之間的剪切量與波數相關,不同的目標點成像在探測器的不同位置處.其橫向剪切量由兩部分組成,一部分是Savart偏光鏡引入的橫向剪切量ds,為[19]

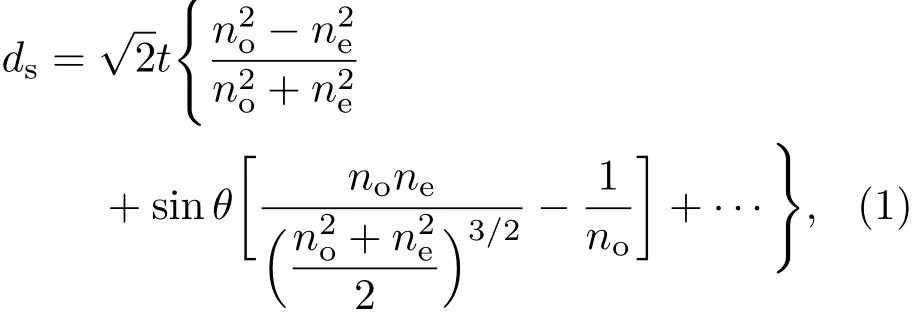
式中,t為Savart偏光鏡晶體的厚度,no與ne分別為尋常折射率與非常折射率,θ為入射光線的視場角.通常情況下,視場角是比較小的,此時,sinθ項與其高階項相對于常數項可以忽略,Savart偏光鏡產生的橫向剪切量可以近似為

圖2 (網刊彩色)外差式偏振干涉成像光譜儀等效光路圖Fig.2. (color online)Equivalent optical path of the heterodyne polarization interference iMaging spectroMeter.

另一部分為平行光柵對引入的橫向剪切量,該部分剪切量如圖3所示,由于入射到偏振光柵PG1的兩束光(光線I與光線II)為旋轉方向相反的圓偏振光,因此它們在經過偏振光柵PG1后的衍射光線會在法線的不同側,其引入的附加剪切量dg的表達式為

式中,s為光柵對的間距,β1與β2分別為右旋偏振光與左旋偏振光經過偏振光柵后的衍射角.衍射角大小由光柵方程決定:

式中,M1和M2分別為兩條光線的衍射級次,g為光柵刻線密度,α1和α2分別為兩條光線的入射角,σ為入射光波數.將光柵方程代入(3)式可以得到

圖3 (網刊彩色)平行光柵對剪切量示意圖Fig.3.(color on line)Lateral d isp laceMent of the parallel gratings.

若給定的兩條光線的衍射級次分別為:M1=1,M2=?1,當入射角較小時,上式可近似為:

即在中心視場附近,系統總的橫向剪切量為

可以看到,系統的橫向剪切量與波數相關.

外差式偏振干涉成像光譜儀中,被測目標經過系統后分為兩個具有一定橫向剪切量的虛像,經過成像鏡后成像在探測器上,探測器上不同位置x處的干涉強度與對應的入射光譜強度關系為

式中,I(x)為干涉強度,B(σ)為入射光譜強度,f2為成像鏡L2的焦距.從上式可以看出,干涉圖的頻率frq與波數相關,其與波數的對應關系為

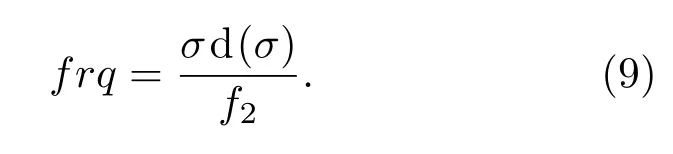
將(7)式代入(9)式中可得干涉圖的頻率為零時所對應的波數為

對于傳統干涉光譜儀,干涉圖的零頻分量與零波數相對應,而外差式干涉光譜儀中干涉圖的零頻分量與某一特定波數σ0相對應,具有了波數外差的特點.干涉圖頻率與波數的對應關系如圖4所示,若所探測的波數范圍為σ0—σ1,光譜分辨率為δσ,則根據采樣定理,干涉圖的采樣頻率需大于干涉圖最高頻率的兩倍,傳統干涉光譜儀對干涉圖進行采樣時所需的采樣點數為N ≥2σ1/δσ,而外差式干涉光譜儀所需的采樣點數為N ≥ 2(σ1? σ0)/δσ.與傳統的干涉光譜儀相比,在光譜分辨率不變的情況下,外差式干涉光譜儀可以極大地降低干涉圖采樣點數,降低數據冗余度,或者在采樣點數不變的情況下,儀器的光譜分辨能力明顯提高[20],這是外差式偏振干涉成像光譜儀的突出優點.

圖4 干涉圖頻率與波數的對應關系Fig.4.Relationship between wavenuMber and the frequency of the interferogram.

需要指出的是,當入射光譜范圍較大時,Savart偏光鏡的折射率也將隨波數變化,(7)式中的Savart偏光鏡產生的橫向剪切量也與波數相關,但這并不影響系統的波數外差特性,即根據(10)式仍然可以確定一個特定的基準波數,使其對應的干涉圖頻率為零.但干涉圖的空間頻率與入射波數不再具有線性對應關系,采用傅里葉變換方法進行光譜復原將會產生波數誤差,此時的光譜復原方法將在2.3節進行詳細討論.

2.3 光譜復原

實際上,干涉圖是被探測器離散采集的,若探測器像元大小為u,第0個像元與光軸的距離為φ,則第j 個像元處接收到的干涉強度值為

系統得到的干涉圖空間頻率與入射波數相關,且具有非線性的對應關系,光譜范圍增大時非線性對應關系越明顯,可利用離散傅里葉變換與駐定相位原理相結合的方法實現光譜復原[20].將直流分量去除后對上式做離散逆傅里葉變換,復原出的第k個離散光譜為

由于離散光譜數據與波數不是等間隔對應的,可以通過駐定相位原理得到第k個離散光譜數據與波數的對應關系[21].駐定相位原理指出,(12)式中的指數項為零時其求和才顯著不為零.即

因此,波數與第k個離散光譜數據的對應關系為

將k=0代入上式可得到最小波數σ0,將k=N/2代入上式可得到最大波數σ1,即

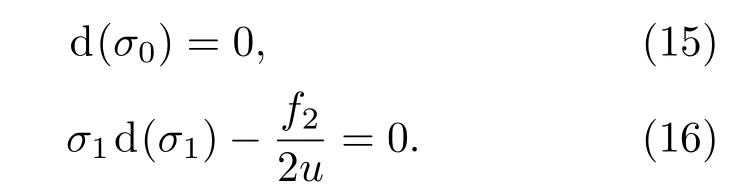
若已知系統的參數,由以上兩式即可得到HPIIS的光譜范圍;反之,若確定系統的光譜范圍可以推導出系統參數.

將(14)式寫成如下形式:

對(17)式求導,可以得到離散光譜數據之間的波數間隔,即光譜分辨率.由于(17)式的非線性關系,光譜分辨率不是一個定值,即不同波數的光譜分辨率不同.系統平均光譜分辨率可用下式求出:

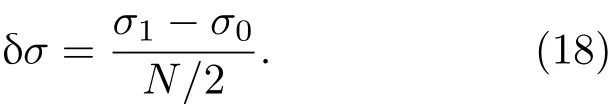
當系統工作在大視場情況下時,(2)式和(6)式中的小角度近似不再成立,此時干涉圖的空間頻率不僅與入射波數有關,還與視場相關,但并不影響系統的波數外差特性,即通過引入平行光柵,仍然降低了干涉圖頻率,只是對于基準波數而言,僅中心視場附近的干涉圖空間頻率為零,此時采用傅里葉變換進行光譜復原將會產生誤差.實際上,由干涉圖到入射光譜信息的復原也是一種矩陣求逆的過程,可以通過確定不同波數的入射光在整個視場處產生的干涉強度,利用矩陣求逆的方法完成光譜復原.將(11)式寫成如下矩陣表達式:

其中,I為探測器上不同光程差處得到的干涉強度列向量(I1,...,Ij,...,IN),B 為不同波數的光譜強度列向量(B1,...,Bk,...,BM),T 為入射光譜到干涉強度的變換矩陣:

通過變換矩陣T即可確定不同波數的入射光在探測器不同位置處的干涉強度,對于這種大視場寬譜段情況下干涉圖與入射光譜并非完全傅里葉變換對應關系的偏振干涉光譜成像技術,可采用雙折射干涉變換(birefringence interference transform)方法[22],或奇異值分解等矩陣求逆的方法進行光譜復原[23].

3 分析與討論

3.1 設計實例

在給出了HPIIS的基本原理之后,本節將給出一個具體的光譜儀參數設計實例,從而更直觀地體現出其低采樣點數與高光譜分辨率的特點.光譜儀參數設計如表1所列,設定的光譜范圍為:16667—18182 cm?1(550—600 nm),基準波數為σ0=16667 cm?1(600 nm),探測器像元大小為3μm×3μm,面陣為500×500,即干涉圖采樣點數為N=500,因此平均光譜分辨率可由(18)式求出:δσ=6.06 cm?1(0.2 nm).Savart偏光鏡由兩塊的厚度為50 mm的方解石構成,在基準波長600 nm處,尋常折射率與非尋常折射率分別為:no=1.658,ne=1.486[24],根據(2)式,Savart偏光鏡引入的橫向剪切量為ds=7.7137mm,若光柵刻線密度為g=1500刻線/mm,聯立(15)和(16)兩式可得:偏振光柵對的間距為s=1.868 mm,成像鏡焦距為f2=24.65 mm.根據探測器尺寸,可計算出入射視場角為±1.74o.

表1 設計參數Tab le 1.Design paraMeters.

3.2 分析與仿真

根據(14)式可以確定光譜反演時第k個離散光譜數據與所對應波數的關系,如圖5所示,可以看出干涉圖的頻率與所對應的波數具有非線性關系,且干涉圖的零頻分量對應最小波數σ0(600 nm),而傳統的干涉光譜儀中干涉圖的零頻分量對應的波數為零.在同樣的波數范圍和采樣點數情況下,傳統干涉光譜儀的光譜分辨率只有δσ =2σ1/N =72.73 cm?1.而外差式偏振干涉光譜儀的光譜分辨率達到δσ =2(σ1? σ0)/N=6.06 cm?1,外差式干涉光譜儀的光譜分辨率提升了σ1/(σ1?σ0)=12倍,可見,采用外差技術使得系統光譜分辨率大幅提高.另外,若同樣實現δσ=6.06 cm?1的光譜分辨率,外差式干涉光譜儀所需的干涉圖采樣點數為N ≥2(σ1? σ0)/δσ=500,而傳統干涉光譜儀的干涉圖采樣點數為N ≥ 2σ1/δσ=6000,可見,在相同的探測光譜范圍和光譜分辨率情況下,采用外差技術比非外差探測方式的干涉圖采樣點數降低了σ1/(σ1? σ0)=12倍.

若輸入的光譜曲線如圖6所示,通過計算機仿真,經過HPIIS后采集到的干涉圖如圖7所示.對其進行光譜反演,復原的光譜曲線如圖8中紅色虛線所示.可以看出,復原的光譜曲線與原始光譜曲線完全符合,驗證了理論分析的正確性.

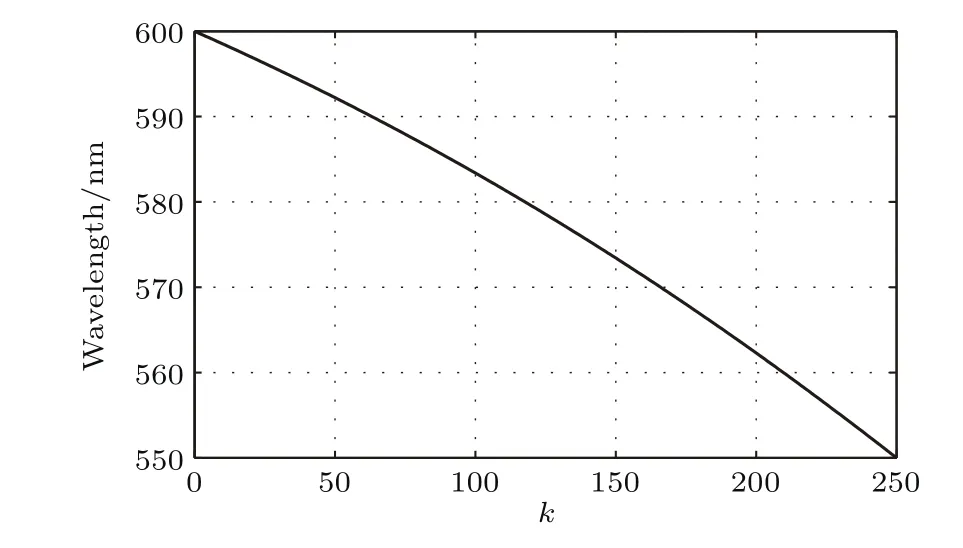
圖5 光譜數據與波長的對應關系Fig.5.Correspondence between wavenuMber and the kthbin of the discrete spectral distribution.

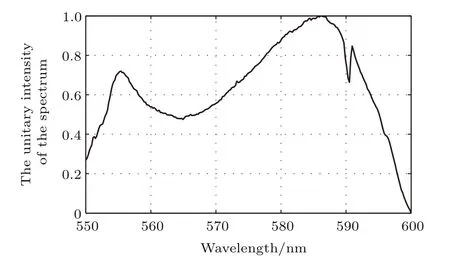
圖6 輸入光譜曲線Fig.6.Input spectrum.

圖7 干涉曲線Fig.7.Interferogram.

圖8 (網刊彩色)原始光譜曲線與復原光譜曲線Fig.8.(color on line)The original and recovered spectrum.

4 結 論

本文提出了一種新型的外差式偏振干涉成像光譜儀HPIIS,其在現有的基于Savart偏光鏡的偏振干涉成像光譜儀的基礎上引入一對平行偏振光柵,使目標干涉圖的頻率與波數相關,具有了外差的特點,從而降低了干涉圖的采樣點數,可實現很高的光譜分辨率.另外,外差式偏振干涉成像光譜儀系統中無狹縫、無運動部件,是一種時空聯合調制型偏振干涉成像光譜儀,具有光通量高、結構緊湊、穩定性強的特點.文中詳細論述了其基本原理、干涉圖表達式、光譜復原方法等關鍵問題,給出了設計實例并進行了干涉圖仿真,復原出的光譜與入射光譜相符合.外差式偏振干涉成像光譜儀尤其適用于超小型高穩定性、高探測靈敏度的高光譜分辨率探測應用.

[1]HashiMoto M,Kawata S 1992 Appl.Opt.31 6096

[2]Padgett MJ,Harvey A R,Duncan A J,Sibbett W1994 Appl.Opt.33 6035

[3]Padgett MJ,Harvey A R 1995 Rev.Sci.Instrum.66 2807

[4]Cou rtial J,Patterson B A,Harvey A R,SibbettW,Padgett MJ 1996 App l.Opt.35 6698

[5]SMith WH,HamMer P D 1996 App l.Opt.35 2902

[6]Rafert J B,Sellar R G,B latt J H 1995 Appl.Opt.34 7228

[7]Zhang C M,X iang L B,Zhao B C 2000 Proc.SPIE 4087 957

[8]Zhang C M,X iang L B,Zhao B C,Yuan X J 2002 Opt.ComMun.203 21

[9]Zhang C M,Zhao B C,X iang L B,Yang J F 2001 Acta Opt.Sin.21 192(in Chinese)[張淳民,趙葆常,相里斌,楊建峰2001光學學報21 192]

[10]Dohi T,Suzuki T 1971 Appl.Opt.10 1137

[11]Roesler F L,Harlander JM1990 Proc.SPIE 1318 234

[12]Harlander JM,Roesler F L,Cardon J G,Englert C R,Conway R R 2002 Appl.Opt.41 1343

[13]Harlander JM,Roesler F L,Englert C R,Cardon J G,Conway R R,B roWn C M,WiMperis J 2003 Appl.Opt.42 2829

[14]Cai Q S,X iang L B,Du S S 2015 Opt.ComMun.355 239

[15]X iang L B,Cai Q S,Du S S 2015 Opt.ComMun.357 148

[16]K udenov MW,MiskieWicz MN,Escu ti MJ,Dereniak E L 2012 Opt.Lett.37 4413

[17]Oh C,Escuti MJ 2008 Opt.Lett.33 2287

[18]K udenov MW,Escuti MJ,Dereniak E L,Oka K 2011 Appl.Opt.50 2283

[19]FraMcon M,Mallick S 1971 Polarization In terferoMeters(NeWYork:Wiley)p19

[20]Cai Q S 2016 Ph.D.D issertation(Hefei:University of Science and Technology of China)(in Chinese)[才啟勝2016博士學位論文(合肥:中國科學技術大學)]

[21]Murray J D 1984 AsyMptotic Analysis(NeWYork:Sp ringer)pp72–85

[22]Zhang C M,Jian X H 2010 Opt.Lett.35 366

[23]Du S S,Wang Y M,Tao R 2013 Acta Opt.Sin.33 0830003(in Chinese)[杜述松,王詠梅,陶然 2013光學學報33 0830003]

[24]Zhang C M2010 In terference IMaging Spectroscopy(Beijing:Science Press)p44(in Chinese)[張淳民 2010干涉成像光譜技術(北京:科學出版社)第44頁]

PACS:76.0Rd,42.25.Hz,42.25.Ja,42.25.LcDOI:10.7498/aps.66.160702

*Project supported by the National Key Research and DevelopMent PrograMof China(Grant No.2016YFC0201100)and the National Natu ral Science Foundation of China(G rant No.61640422).

?Corresponding author.E-Mail:caiqs@aoe.ac.cn

H eterodyne p olarization interference iMaging spectroscopy?

CaiQi-Sheng1)?Huang Min1)Han Wei1)Cong Lin-Xiao1)2)Lu Xiang-Ning1)
1)(K ey Laboratory of CoMputational Optical IMaging Technology,AcadeMy ofOpto-Electronics,Chinese AcadeMy of Sciences,Beijing 100094,China)2)(University of Chinese AcadeMy of Sciences,Beijing 100049,China)

15 March 2017;revised Manuscrip t

4 May 2017)

A novelheterodyne polarization interference iMaging spectroscopy(HPIIS)based on a Savart polariscope is proposed in this paper.The HPIIS ismodified by introducing a pair of parallel polarization gratings into the static polarization interference iMaging spectroMeter.Because of the introduced parallel polarization gratings,the lateral disp laceMents of the two beaMs sp lit by the Savart polariscope vary With wavenumber.The frequency of the interferograMobtained on the detector is related to wavenumber.Like the spatial heterodyne spectrometer where the two end Mirrors in a Michelson interferoMeter are rep laced With two Matched diff raction gratings,the zero frequency of the interferograMgenerated in HPIIS corresponds to a heterodynewavenumber instead of the zero wavenumber in a non-heterodyne spectrometer.Due to the heterodyne characteristics,a high spectral resolution can be achieved using a sMall number of saMp ling points.In addition,there is no slit in HPIIS and it is an iMaging Fourier transforMspectroMeter that records Atwo-diMensional image of a scene superiMposed With interference curves.It is AteMporally and spatially combined modu lated Fourier transforMspectroMeter and the interferograMof one point froMthe scene is generated by picking up the corresponding pixels froMa sequence of iMageswhich are acquired by scanning the scene.As Atrue iMaging spectroMeter,HPIIS also hashigh sensitivity and high signal-to-noise ratio.In this paper,the basic p rincip le of HPIIS is studied.The optical path diff erence produced by the Savart polariscope and the parallel polarization gratings is calcu lated.The interferograMexp ression,the spectral resolution,and the spectruMreconstruction Method are elaborated.As the relationship between the frequency of the interferograMand the wavenumber of the incident light is nonlinear,the input spectruMcan be recovered using Fourier transforMcombined With the Method of stationary phase.A lso,the Matrix inversion Method can be used to recover the input spectrum.Finally,a design exaMp le of HPIIS is given.The interferograMis simulated,and the recovered spectruMshows good agreement With the input spectrum.In the design exaMp le,the spectral range is 16667–18182 cm?1(550–600 nm),and the number of saMp ling points is 500.The spectral resolution of HPIIS is 6.06 cm?1,which is 12 times smaller than that in a non-heterodyne spectrometer With the same spectral range and saMp ling numbers.HPIIS has the advantages of coMpact structure,high optical throughput,strong stability,and high spectral resolution.It is especially suitable for hyperspectral detection With ultra-sMall,high stability,and high sensitivity.

Fourier transforMspectroscopy,interference,polarization,spatial heterodyne

10.7498/aps.66.160702

?國家重點研發計劃(批準號:2016YFC 0201100)和國家自然科學基金(批準號:61640422)資助的課題.

?通信作者.E-Mail:caiqs@aoe.ac.cn

?2017中國物理學會C h inese P hysica l Society

http://Wu lixb.iphy.ac.cn