基于形態(tài)學的鉆石式琢型人工寶石計數方法

孫紹華, 玉振明

(1.桂林電子科技大學 信息與通信學院，廣西 桂林 541004；2. 梧州學院 圖像處理與智能信息系統(tǒng)廣西高校重點實驗室，廣西 梧州 543002)

基于形態(tài)學的鉆石式琢型人工寶石計數方法

孫紹華1, 玉振明2

(1.桂林電子科技大學 信息與通信學院，廣西 桂林 541004；2. 梧州學院 圖像處理與智能信息系統(tǒng)廣西高校重點實驗室，廣西 梧州 543002)

文章針對鉆石式琢型人工寶石結構的特點，提出了一種基于形態(tài)學的人工寶石自動計數方法。利用寶石成像的幾何形狀特征，找出單粒寶石的標準面積，自適應地計算寶石直徑，通過采用與寶石直徑相關的圓形結構元素進行快速的形態(tài)學腐蝕分離粘連的寶石并完成計數。此方法相對簡單，計算量小，實驗結果顯示可以滿足大批量人工寶石自動準確快速計數的要求。

人工寶石；鉆石式琢型；圖像處理；形態(tài)學；計數

0引言

立方氧化鋯[1]的折射率為2.15-2.18，色散為0.06，與鉆石的2.42和0.044非常接近，因與鉆石具有相近的物理特性進而被人工合成和加工成為人工寶石(以下簡稱寶石)。寶石作為鉆石的代替品被成功地推向市場，并因物美價廉而廣受歡迎。廣西梧州成為目前世界上最大的人工寶石加工和貿易集散基地，加工量約占全國的80%，占世界總量的40%以上，梧州市已被世界珠寶界譽為“人工寶石之都”[2-3]。人工寶石通常以顆粒數為單位，梧州的人工寶石年產量超過130億粒，每次的生產或交易的數量通常可達數萬粒甚至數十萬粒。人工寶石的計數量非常大，采用人工計數成本高，準確性低，勞動強度大，而且寶石的高反光特性對人眼乃至人體傷害都非常大。隨著圖像技術的發(fā)展成熟，基于圖像的計數方法被廣泛地研究和應用，如醫(yī)學上通過顯微鏡下等采集細胞圖像進行計數并用于醫(yī)學診斷[4-5]，農業(yè)上采集蔬菜、水果、棒材等圖像進行計數以評估產量、優(yōu)化莊園管理等[6-8]。因此，我們嘗試將圖像處理技術引入到人工寶石計數上。

寶石的結構特殊，需要分析成像中的寶石特征，尋找一種自適應的計數方法，同時該方法要求有高的計數效率和準確率，因此該方法應該盡可能做到簡單、計算量少，以滿足大批量寶石交易時的計數要求。采用圖像處理技術對研究對象進行計數，關鍵是對象與背景的分割以及對象之間發(fā)生重疊或者粘連時的分割和計數。醫(yī)學上主要基于形態(tài)學及基于邊緣跟蹤兩大類方法，張潔[9]等從基礎理論和實際算法的角度進行描述和歸類，分析和比較了腐蝕膨脹法、測地重建、分水嶺、鏈碼差法和矢量點積和叉積法、估算圓心法等；X.Z Bai等[4]提出用凹點和橢圓擬合分離接觸的細胞；蔡競等[10]基于細胞近圓的特點提出基于Hough變換圓檢測的粘連細胞分離方法； X. Bai[11]提出對接觸的細胞核子利用最短路徑尋找分離線算法。其他如農業(yè)等利用RGB圖像中的高光球面反射峰值進行檢測[6-7]，利用對象顏色、紋理等特征進行分割[10]。不同的算法適用范圍、優(yōu)缺點不盡相同。到目前為止，還沒有通用的粘連對象分離理論，只有根據具體的情況采取較為有效的方法。

寶石被加工為特殊的結構，在寶石圖像中幾何形狀是刻畫寶石的好特征。對圖像中的幾何形狀提取方法M.Q Yang等[12]給出了綜合性的描述，S. Sinkeviciu等[13]利用形狀特征和顏色對琥珀進行了鑒別。利用圖像處理方法對寶石進行自動計數的難點在于粘連寶石的計數。針對鉆石式琢型寶石的特殊結構，本文提出了一種基于形態(tài)學運算的寶石粘連分離方法，該方法利用寶石的結構特征、構造結構元素及其參數，可以快速自適應地進行分離，進而可以實現(xiàn)寶石快速自動計數。

1鉆石式琢型寶石結構與特征

1.1鉆石式琢型寶石結構

根據全內反射原理，寶石常琢磨成圓多面型，其結構及名稱如圖1所示[1-2]，該琢型常用于鉆石，因此也稱為圓鉆型或鉆石式琢型，可以分為冠部(Crown,C)、腰部(Girdle,G)和亭部(Pavilion, P)3大部分。其中，上面的冠部共有33個小面，包括中間為一個正八邊形的桌面(Table，也稱臺面)和8個冠部主刻面、8個三角形的星刻面以及16個上腰小面；中間薄薄的一圈為寶石的腰部，腰部的寬度為寶石的直徑(D)也稱為寶石的寬；下面部分為亭部，由16個下腰小面和8個亭部主刻面以及底部的底小面(亭尖)構成。該琢型的刻面從中心向外呈放射狀排列，使進入寶石的光從亭部很少漏出，以增加其亮度，因此該琢型也被稱之為圓明亮琢型。在不同的文獻和應用場合中，三大部分的比例略有變化，試驗中取各部分與寶石直徑的比例關系為：

臺寬比：RT=T/D=0.58(±0.05)，

亭寬比：RP=P/D=0.43(±0.03)，

冠寬比：RC=C/D=0.14(±0.03)，

腰厚：RG=G/D=0.03(±0.02)。

1.2 鉆石式琢型寶石成像特征

由于不同大小或類別的寶石有不同的價格，因此在寶石生產和交易過程中，寶石都按不同的大小和類別進行了分類，所以寶石的計數中每一批次的寶石具有相同的形狀和大小。假設攝像頭垂直安裝于寶石所在的平面，使寶石隨機靜止呈現(xiàn)在平臺上，則圖像中的寶石為處于對應支撐面時的俯視圖。

由文獻[14]中可知，單粒寶石隨機靜止時處于桌面或者亭部為支撐面，利用計算機輔助設計軟件PRO/E對寶石結構進行可視化構建如圖2所示，分別為寶石處于桌面或者亭部為支撐面靜止時的各視平面圖，其中，最下方的為對應支撐面的俯視圖。

當寶石處在桌面為支撐面時，寶石的俯視圖為圖2(a)中下方的近似的圓形，其直徑等于寶石直徑，其對應面積為：

(1)

當寶石處在亭部為支撐面時，寶石的俯視圖為圖2(b)中下方的近似的橢圓形，其長軸為寶石的直徑，短軸為寶石腰部在支撐面的投影并記為a。設此時腰部與支撐面的夾角為A，該夾角大小等于寶石亭部角度，則

(2)

(3)

當寶石不完全處于相機或者光源的正下方時，寶石成像圖中除了呈現(xiàn)為圓形、橢圓形外還可能出現(xiàn)其他形狀，如圖2中近似五邊形等。由寶石結構及其成像圖可知，所有單粒寶石成像后具有兩個共同特征，一個特征是所有的寶石圖像都為凸形，另一個特征是長度等于寶石的直徑，即

LC=LE=LP=LO=D

(4)

其中LC、LE、LP、LO分別為圓形(C)、橢圓形(E)、五邊形(P)及其他(O)形狀寶石的長度。由圖2中可知，五邊形是寶石的軸向剖面圖的近似，是因腰部的厚度很小所產生的效果，其寬度為寶石的整個高度H即冠部、腰部和亭部高度之和

H=C+G+P=0.6D

(5)

因此，寶石成像后的寬度范圍(0.6～1)D。

2寶石計數原理及方法

2.1 形態(tài)學處理原理

數學形態(tài)學基本思想是用具有一定形態(tài)的結構元素去度量和提取圖像中對應形狀已到達對圖像分析和識別的目的[15]。因此，形態(tài)學運算效果取決于結構元素的大小、內容以及邏輯運算的性質。腐蝕和膨脹是二值圖像中常見的形態(tài)學運算。腐蝕是一種消除邊界點，使邊界向內部收縮的過程。除此，腐蝕運算還可以消除孤立的噪聲點。膨脹是將與目標區(qū)域相接觸的所有背景點融合至目標區(qū)域的過程，因此會使目標變大，而內部孔洞減小。另外膨脹運算也可以擴大目標區(qū)域的面積，使其形成連通域。它們的實現(xiàn)如下：

設A為圖像的目標區(qū)域集合，B為結構元素，則A用B腐蝕被定義為

A?B={x|Bx?A}

(6)

A用B膨脹定義為

A⊕B={x|Bx∩A?A}

(7)

其中，Bx代表了結構元素B在平移了x后的變換值。

運用腐蝕運算與膨脹運算的組合即可達到對二值圖像的粘連分割目的。對于重疊粘連的目標，運用多次腐蝕運算將其分離成獨立的幾個單體目標，然后分別對分離后的各個目標進行與腐蝕次數相同的膨脹運算，從而找出與原目標面積相同的物體[9]。運用數學形態(tài)學方法對研究對象進行分割，原理及其實現(xiàn)都要比分水嶺、基于邊緣跟蹤等方法簡單。寶石的結構獨特但是最大長度都相同，而且形狀也比較接近，為了滿足快速計數的需求，可以通過形態(tài)學的快速處理實現(xiàn)計數。此外，寶石在圖像中大多數接近于圓形，因此我們可以采用圓形為結構元素，那么關鍵的參數就是圓形結構的半徑選擇了。

2.2寶石形態(tài)學結構參數及獲取

根據第1.2的分析，圖像中寶石的寬度在(0.6～1)D范圍內，為了保證沒有寶石在形態(tài)學處理過程中被腐蝕掉，需滿足圓形結構元素的半徑Rse為：

Rse<0.6D

(8)

另一方面，為了快速分離粘連的寶石要求圓形結構元素的半徑盡可能大。因此，不失一般性地，我們可以選擇圓形結構元素的半徑為：

Rse=0.5D

(9)

由此可見，寶石的直徑D是決定粘連寶石分割乃至整個計數結果準確性的關鍵。

圓形度是刻畫圖像各連通區(qū)域與圓的接近程度[15]。由文獻[14]和1.2分析，我們可以通過將圖像中的高圓形度連通區(qū)域挑選出來作為單粒圓形寶石，并計算它們的面積均值作為單粒寶石面積SC，再根據式(1)獲得寶石的直徑

(10)

3算法實現(xiàn)及實驗測試

3.1算法流程及實現(xiàn)

為了提高計數的準確度，通過機械裝置[16]將寶石盡量地分散，使寶石隨機靜止散開在實驗平臺上。將攝像頭垂直安裝在寶石所在的平面上。計數流程如圖3所示，具體過程如下：

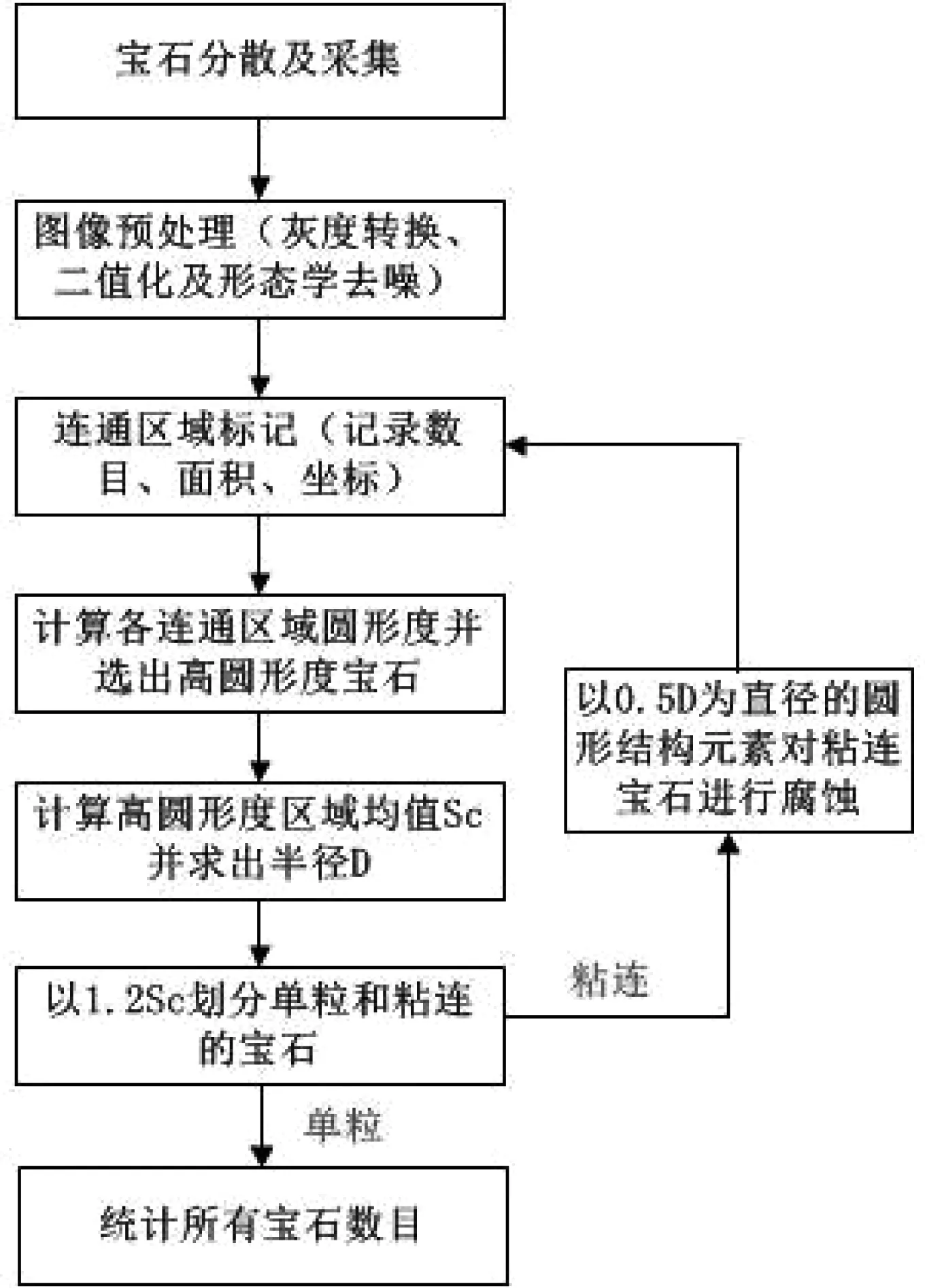
圖3 寶石計數流程圖

圖4 寶石圖像 (a)原圖；(b)預處理后

Step1： 通過機械裝置將寶石分散，并由圖像采集系統(tǒng)自動獲取寶石圖像，如圖4(a)。

Step2： 圖像預處理。為了提高計數速率，將圖像轉化為灰度圖像，并進行二值化和形態(tài)學預處理，平滑邊界，去除背景和噪聲，如圖4(b)。

Step3： 對連通區(qū)域進行標記，采用8領域連通法對圖像進行標記，記錄連通區(qū)域數目及每個區(qū)域的面積和邊界坐標等。

Step4：計算每個連通區(qū)域的圓形度，并選出圓形度接近于1的高圓形度區(qū)域(試驗中選取0.9)作為單粒圓形寶石。

Step5：對所選出的高圓形度區(qū)域求面積均值得到單粒寶石面積SC，進而計算出寶石的直徑D。

Step6：將寶石分類。根據文獻[14]單粒寶石成像面積范圍為(0.63—1)SC，考慮的實際情況不是一般地，當區(qū)域面積范圍為(0.5—1.2)SC認為是單粒寶石，當大于1.2是判斷該區(qū)域寶石發(fā)生粘連，如圖5(a)(b)為寶石分類的結果。

Step7： 對分類后判別為粘連的寶石進行形態(tài)學處理，即采用半徑為0.5D的圓形結構元素進行腐蝕操作，圖5(c)為腐蝕后的結果。

Step8：經過上述步驟后寶石基本上都可以分離，除非少數由于寶石的強反光作用或者重疊。為了解決此問題，重復Step3至Step7，直到可完全分離所有粘連的寶石。實際中，一般只需要做2-3個循環(huán)即可滿足準確計數的要求。

圖5 寶石分類圖(a)單粒；

(b)粘連；

(c)粘連寶石分離圖(一次腐蝕)

為了清晰寶石計數的結果，在已計數的寶石的中心上標記“*”，如圖6所示。該結果只需要運行2次形態(tài)學腐蝕即可完成計數，從圖上可以清晰看出，寶石均已被標記上“*”，即準確計數。

圖6 寶石計數標記圖

3.2 實驗測試及性能分析

為了進一步說明本算法的可行性，通過隨機采集不同粘連條件下的不同尺寸的寶石進行測試，如圖7和圖8所示。其中，圖7(a)、(b)的寶石直徑為3.5mm，(c)、(d)的寶石直徑為4.5mm，(a)、(c)的寶石只是輕微粘連的，而(b)、(d)的寶石粘連較為嚴重。圖8是與圖7對應的經過分離后，對已計數的寶石重心進行了標注的結果圖。

(a)D=3.5mm

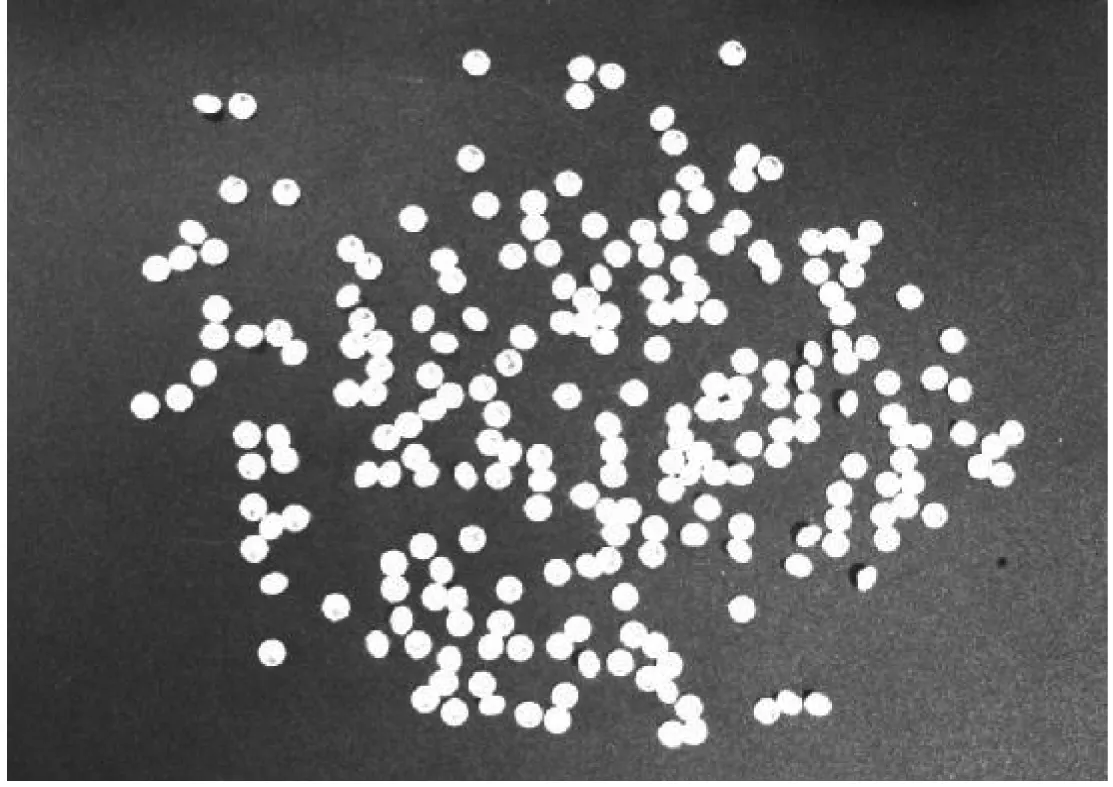
(b)D=3.5mm

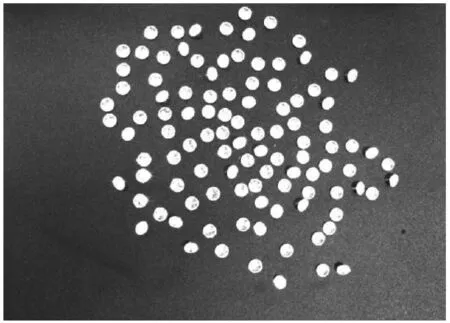
(c)D=4.5mm

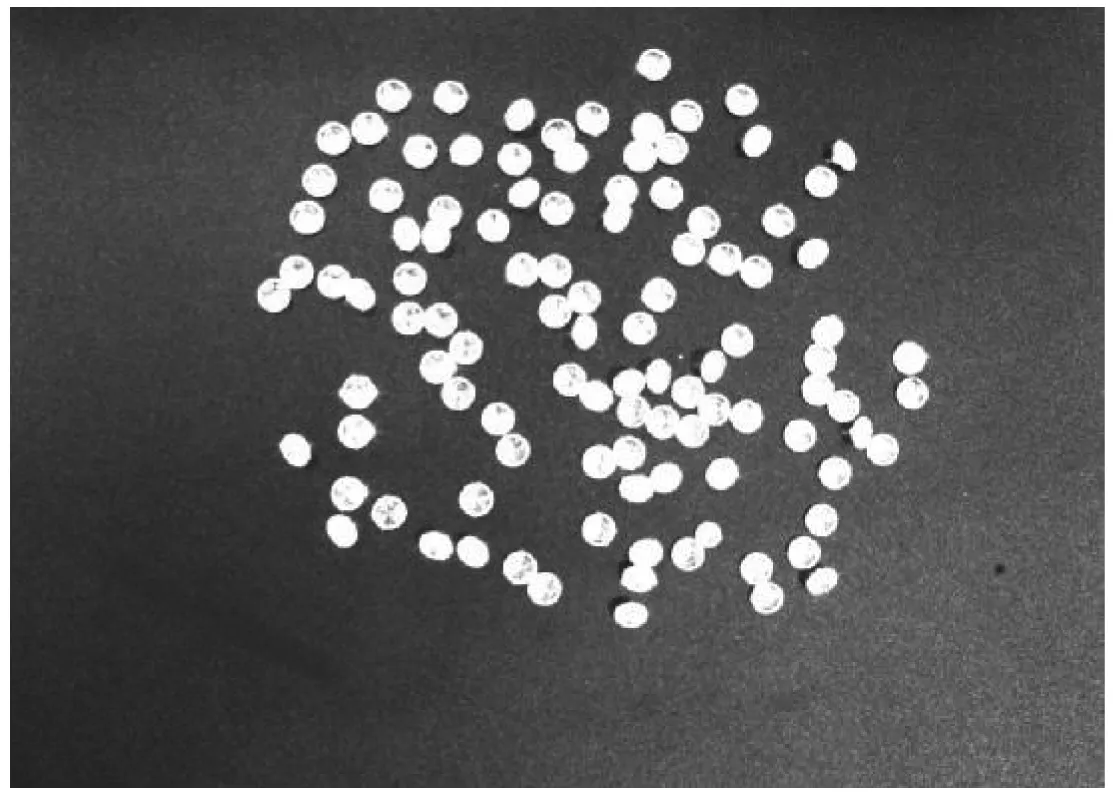
(d)D=4.5mm

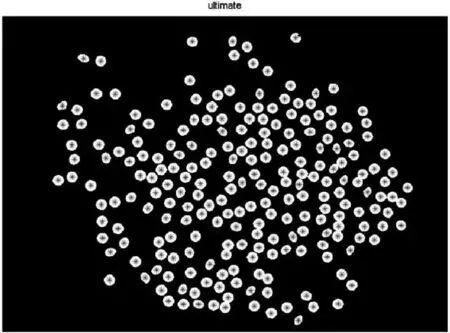
(a)D=3.5mm

(b) D=3.5mm

(c)D=4.5mm

(d)D=4.5mm

從計數標記結果圖可以看出， 除了圖7(b)中有3個寶石區(qū)域未被準確計數外，其他圖中的寶石都已100%的計數。圖7(b)中未被準確計數的原因是該區(qū)域的寶石相互緊靠，接觸面的寬度接近于寶石的直徑，因而無法通過形態(tài)學腐蝕分離，但是準確率仍可達97.8%。為了進一步說明算法的可行性，與利用圖像連通區(qū)域直接計數法和手工計數法作比較，性能比較詳見表1和圖9所示，其中，表1和圖9中的(a)-(b)分別對應圖7(a)-(b)的各子圖。可以看出算法具有準確率高、計數速率快、性能穩(wěn)定等優(yōu)勢。

表1 不同計數方法下的性能數據

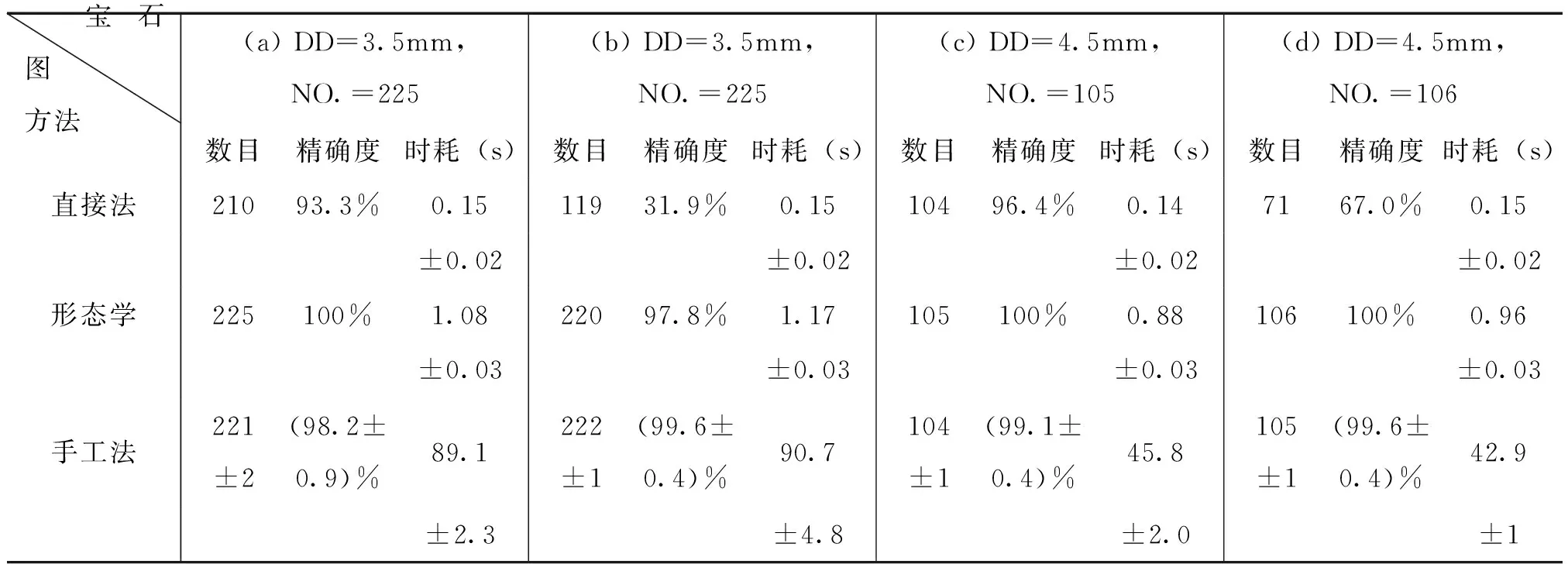
寶石圖方法(a)DD=3.5mm,NO.=225(b)DD=3.5mm,NO.=225(c)DD=4.5mm,NO.=105(d)DD=4.5mm,NO.=106數目精確度時耗(s)數目精確度時耗(s)數目精確度時耗(s)數目精確度時耗(s)直接法21093.3%0.1511931.9%0.1510496.4%0.147167.0%0.15±0.02±0.02±0.02±0.02形態(tài)學225100%1.0822097.8%1.17105100%0.88106100%0.96±0.03±0.03±0.03±0.03手工法221±2(98.2±0.9)%89.1222±1(99.6±0.4)%90.7104±1(99.1±0.4)%45.8105±1(99.6±0.4)%42.9±2.3±4.8±2.0±1

圖9 不同計數方法下的性能

4結束語

通過對寶石結構的研究，分析寶石在成像中的幾何形狀特征，得出單粒寶石在成像中的形狀均為外凸形狀而且最大長度等于寶石的直徑，最小寬度為寶石剖面所在的平面圖對應的寬度，利用此特征獲得形態(tài)學處理結構元素的參數。同時，通過計算各個連通區(qū)域的圓形度，進一步找出高圓形度連通區(qū)域的面積，計算出寶石的直徑，從而可以自適應地通過采用與寶石直徑相關的圓形結構元素進行快速的形態(tài)學腐蝕分離粘連的寶石，進而完成寶石的計數。通過實驗測試對于隨機放置的粘連寶石，本算法的計數效率可達97%以上；當利用機械裝置進行寶石數目控制和分散時，其計數準確率基本上可達100%。整個寶石計數過程可以自動完成，而且采用方法較為簡單，計算量小，可以滿足大批量寶石的自動、快速計數。為了快速計數采用較為簡單的形態(tài)學分離方法，準確率雖然已經較高，但還可以進一步尋找更佳的算法來提高分離的準確性并應用于后續(xù)的寶石檢測等方面。

[1]韓秀麗，陳穩(wěn)，李昌存.寶石知識與鑒賞[M].北京：冶金工業(yè)出版社：2014.

[2]高濤.基于眾籌模式的梧州人工寶石產業(yè)升級研究[J].全國商情(經濟理論研究)，2016(12):76-77.

[3]王坤,周樹禮,張琳琳,等.長盛不衰的梧州人造寶石加工業(yè)[J].超硬材料工程,2011(6):54-58.

[4]X. Z Bai, C. M Sun, F. G Zhou. Touching Cells Splitting by Using Concave Points and Ellipse Fitting [J]. Digital Image Computing: Techniques and Applications, 2008.11:271-278,DOI 10.1109 .

[5]B. Chaudhury, K. Kramer, D. Elozory, et al., A Novel Algorithm for Automated Counting of Stained Cells[C]. Proceedings of the 25th IEEE International Symposium on Computer-Based Medical Systems,2012. DIO:10.1109/CBMS.2012.6266296.

[6]D. Font, T. Pallejà, M. Tresanchez, et al., Counting red grapes in vineyards by detecting specular spherical reflection peaks in RGB images obtained at night with artificial illumination[J]. Computers and Electronics in Agriculture, 2014,108:105-111.

[7]J. M. Walter, B. J. Carlos. Automatic green fruit counting in orange trees using digital images[J]. Computers & Electronics in Agriculture. 2016, 127：572-581.

[8]R. Linker, O. Cohen , A. Naor .Determination of the number of green apples in RGB images recorded in or-chards[J]. Computers and Electronics in Agriculture, 2012,81:45-57.

[9]張潔,胡平.粘連細胞分離算法綜述[J].計算機與數字工程,2008,6(36):53-56,81.

[10]蔡競,龐全.一種強粘連細胞圖像的分割方法與實現(xiàn)[J].機械制造, 2011,49(560):27-30.

[11]X.Bai, et al.Finding splitting lines for touching cell nuclei with a shortest path algorithm[J].Computers in Biology & Medicine, 2015,8:277-286.

[12]M. Q. Yang, K. Kpalma and J. Ronsin. A survey of shape feature extraction techniques[J]. Pattern Recognition, 2008,11:43-90.

[13]S. Sinkevicius, A. Lipnickas, K. Rimku. Automatic amber gemstones identification by color and shape visual properties[J]. Engineering Applications of Artificial Intelli-gence, 2015,37:258-267.

[14]潘明華.圓明亮琢型寶石隨機平衡特征的研究[J].科學技術與工程,2015,28(15):170-173,178.

[15]Rafael C. Gonzalez .數字圖像處理的MATLAB實現(xiàn)[M].2版.阮秋琦,譯. 北京：清華大學出版社,2013.

[16]潘明華,韋衡冰,鄧小林,等.一種基于圖像的自動寶石計數裝置[P]. 中國：201510431014.3，2015-12-09.

(責任編輯：覃華巧)

Counting Method of Brilliant Cut Artificial Gems Based on Morphology

Sun Shaohua1, Yu Zhenming2

(1.School of Information and Communication, Guilin University of Electronic Technology, Guilin 541004, China;2.Guangxi Colleges and Universities Key Laboratory of Image Processing and Intelligent Information System, Wuzhou University, Wuzhou 543002, China)

According to the special structure of brilliant cut gems, an automatic counting method for artificial gems was proposed based on morphology. According to the characteristics of shapes of gems in image, the standard area of a single gem has been found and the diameter of a single gem has been obtained adaptively. Using circular structure element with the diameter associated with gems, the adhesive gems can be separated rapidly by morphology corrosion. This method is relatively simple and involves less calculation. The experimental results shown that it can satisfy the requirements of rapid and automatic counting of large quantities of artificial gems.

Artificial gems; Brilliant cut; Image Processing; Morphology; Counting

2017-03-30

梧州學院科研重點研究項目(2015B008)

TP399;TS93

A

1673-8535(2017)03-0001-09

孫紹華(1982-)，男，山東臨沂人，桂林電子科技大學信息與通信學院碩士研究生，研究方向：圖像處理、智能控制。

玉振明(1963-)，男，廣西梧州人，梧州學院副院長，教授，研究方向：圖像處理、自適應信號處理和電機控制等。