淺析“繩、桿速度牽連模型”

宋海峰

(江蘇省天一中學，江蘇 無錫 214101)

淺析“繩、桿速度牽連模型”

宋海峰

(江蘇省天一中學，江蘇 無錫 214101)

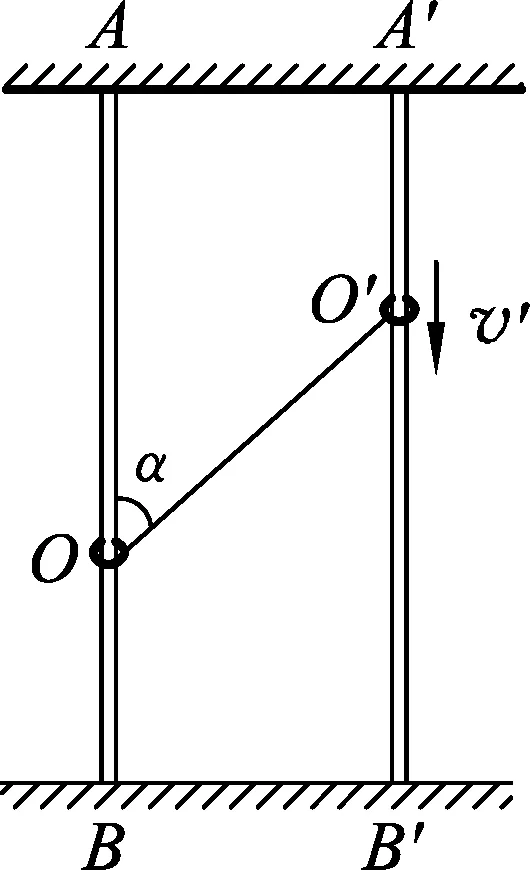
圖1

“繩、桿速度牽連模型”是高中物理教學中的一個難點,也是各高校自主招生和競賽出題的熱點．對一些簡單的、常見的“繩、桿速度牽連模型”,學生由于平時的反復訓練基本能應付外,對一些稍微復雜、陌生的“繩、桿速度牽連模型”,學生在處理時就常常會思維混亂進而無從下手．究其原因,就是學生對此類問題只會生搬硬套,知其然而不知其所以然．筆者在輔導學生自主招生時布置了一道相關習題,根據學生的作業反饋談談此類問題常見錯誤及原因和一般處理的方法．

1 題目

圖2

如圖1所示,兩只小環O和O′分別套在靜止不動的豎直桿AB和A′B′上,一根不可伸長的繩子一端系在A′點上,穿過環O′,另一端系在環O上．若環O′以恒定速度v′向下運動,當∠AOO′=α時,求環O的速度v?

2 常見錯誤及原因分析

常見錯誤1.環O′以v′向下運動,繩子O′A′以v′向上運動,繩子不可伸長,則繩子O′O以v′斜向上運動,再將v′分解到豎直方向和水平方向,如圖2所示,則v′在豎直方向上的分量就是環O的速度,即v=v′cosα.

原因分析：造成上述錯誤的原因,就是沒有分清合運動與分運動的概念,錯誤地認為繩子O′O的速度v′就是環O的合速度(合運動),因此將v′直接進行分解．這里涉及合運動的概念,何為合運動?物體實際的運動就是合運動．顯然,環O由于桿AB的約束,實際豎直向上運動,這個運動才是合運動,將這個合速度按效果沿繩子和垂直繩子分解才合理．

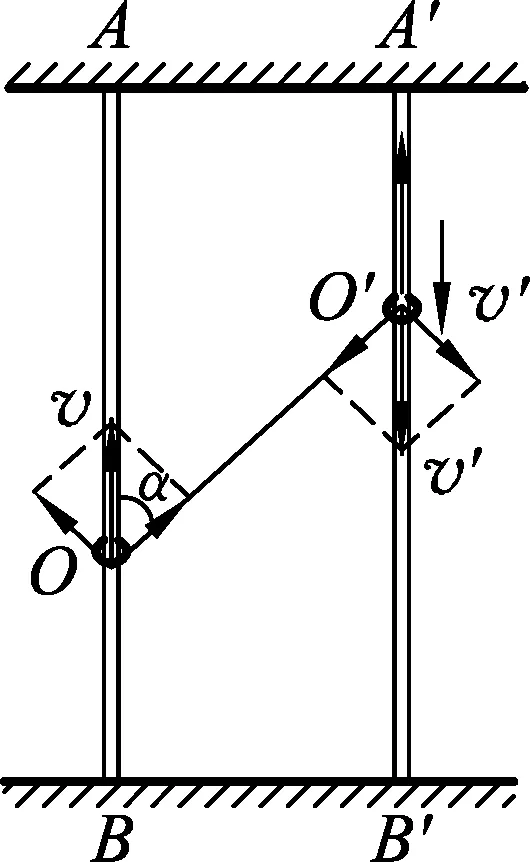
圖3

常見錯誤2.如圖3所示,把環O和環O′的速度分解,然后根據速度關聯問題中的結論“剛性繩、桿上各點在同一時刻具有相同的沿繩、沿桿的分速度”,即v′cosα=vcosα,得v=v′．

原因分析：此種解法雖然分清了合運動和分運動的概念,抓住了環O、環O′的合運動,但生搬硬套速度關聯問題中“剛性繩、桿上各點在同一時刻具有相同的沿繩、沿桿的分速度”的結論,而未注意到將環O、環O′速度分解后兩分速度方向相反,即相向運動,其效果是使繩子縮短,它們根本不可能相等．所以在使用一些有用結論的同時,要注意知識遷移的條件,避免出現表面類似但本質不同的知識之間,在遷移過程中產生相互干擾和破壞,即產生負遷移．

3 正確的解法

方法1.微元法.

設經過時間Δt,環O、環O′前進的位移分別為

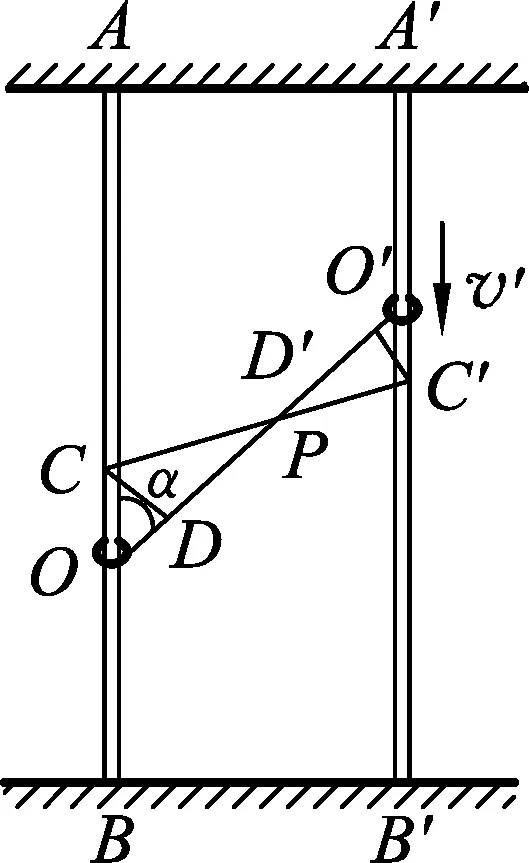
圖4

點評:使用微元法時可設想物體發生一個微小位移,分析由此引起的牽連物體的位移,再找到位移間的關系,進而求出牽連物體間速度的關系．微元法是分析、解決物理問題的常用方法,它貫穿于高中物理知識體系．作為大學知識在高中物理中的應用,“微元法”不但可以豐富學生處理問題的方法,而且可以拓展學生的思維．對于高三的學生特別是要參加自主招生的學生,應當熟練掌握．教師在平時的教學中可以不斷向學生滲透,潛移默化,優化學生的思維品質．

方法2.速度分解法.

類比:如圖5所示,甲車用繩子通過定滑輪以不變的速度v1拉水平面上的乙車,當繩與水平方向成α角時,求乙車的速度v2?

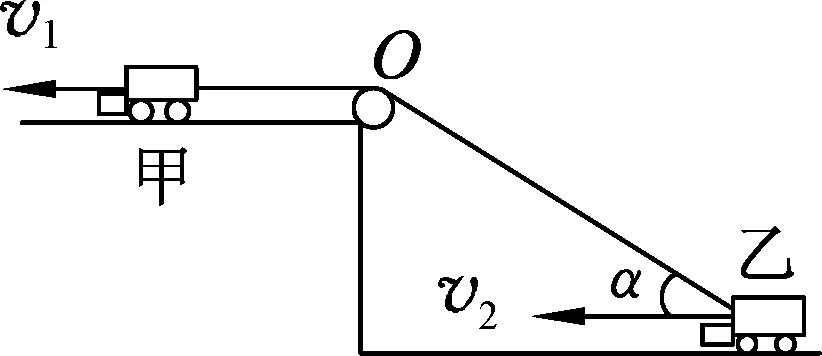
圖5

圖6

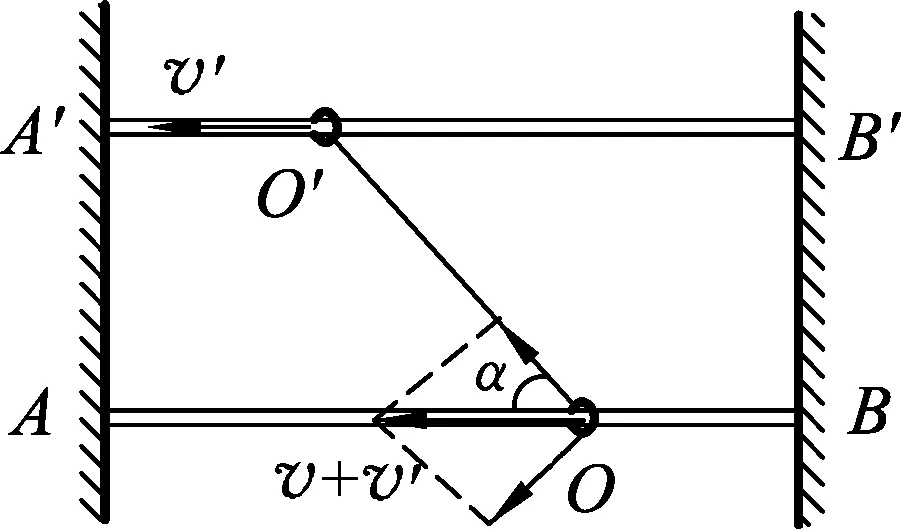
圖7

基于“繩子不能伸縮”,繩子上各點的速率應該相等,甲車運動的速率就是繩子運動的速率,而乙車的實際速度為v2,方向水平向左,將其沿繩子和垂直繩子分解,如圖6所示,則v1=v2cosα.

點評:使用速度分解法的前提是正確判斷研究對象的合運動(實際運動),分析清楚分運動產生的實際意義和效果,這一點是解答問題的關鍵．此方法中,筆者靈活選取環O′為參考系,采用類比法將復雜的、陌生的情景轉化為學生熟悉的情景,使所求問題簡單化,易于學生理解和接受,從而起到幫助學生鞏固知識、加深認識和提高能力的作用．教師在平時的教學中要注重引導學生通過聯想、類比等方法,找出新舊事物在認知結構中共同的本質東西,充分利用遷移規律,由已知悟出未知,舉一反三、觸類旁通地去分析解決問題,從而提升學生的核心素養．

方法3.應用能量轉化及守恒定律.

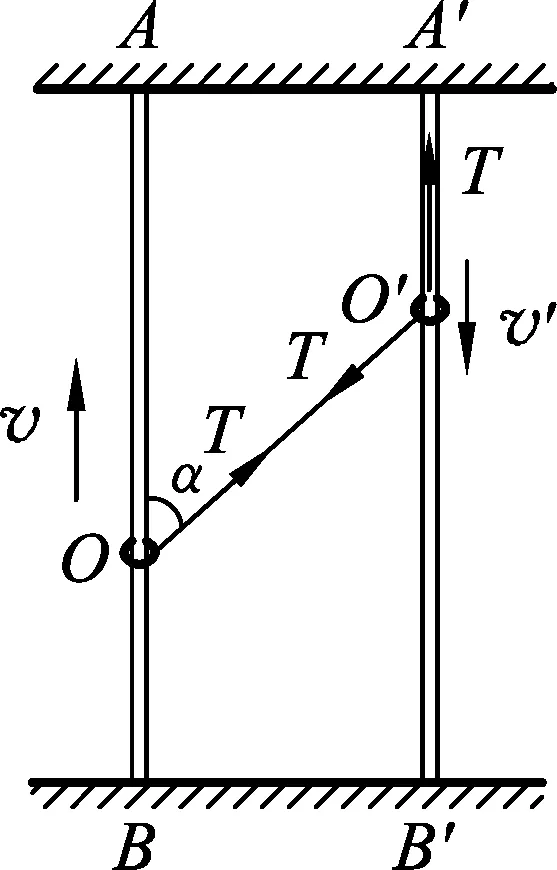
圖8

點評:顯然這種方法不僅計算簡單而且學生也易于理解,但處理此類問題時要注意不能直接計算繩子對兩個環做的功,因為功是一個過程量,而題目要求的速度是一個瞬時量,所以我們可以轉化為繩子做功的瞬時功率為0來處理,同時也要注意使用瞬時功率公式P=Fvcosα時不能忘了夾角．

思維是世界最美麗的火花,教師在教學中要結合解題突出學生創新思維的訓練,不僅可使學生的“學”時刻保持機敏狀態,激發求知、求異、求新的興趣,而且換個角度,換個思維,或許暫時的困頓就柳暗花明了．

2017-02-13)