非晶合金及合金液體的局域五次對稱性?

李茂枝

(中國人民大學物理系,北京 100872)

(2017年6月1日收到;2017年7月18日收到修改稿)

非晶合金及合金液體的局域五次對稱性?

李茂枝?

(中國人民大學物理系,北京 100872)

(2017年6月1日收到;2017年7月18日收到修改稿)

簡要回顧了從20世紀30年代至今,有關非晶合金及合金液體的局域結構五次對稱性的實驗、理論和模擬研究.在簡單液體的早期研究中,人們已經意識到五次對稱性在簡單液體的無序結構、過冷和晶化等起著重要作用,二十面體短程序作為五次對稱性的典型代表受到了廣泛關注.自從Frank提出簡單液體中二十面體短程序的結構單元,大量的理論和實驗研究已經明確在簡單液體、合金液體和金屬玻璃中存在局域五次對稱性,并且建立了局域五次對稱性與合金液體復雜動力學行為、玻璃轉變、液體-液體相變以及非晶合金的形變等統一的定量描述和物理圖像,表明了局域五次對稱性作為結構參量的簡單、普遍和有效性.

非晶合金,合金液體,局域五次對稱性

1 引 言

探索物質的微觀結構特征及其與宏觀性能之間的關系一直是凝聚態物理和材料科學領域的核心科學問題.非晶合金和合金液體的結構長程無序,非常復雜,現代微觀結構分析和表征技術對其結構的分析能力非常有限,也無法用現代晶體學對其認識和理解,所以建立非晶合金和合金液體的微觀結構和宏觀性能的關系一直是科學難題[1].難點主要體現在以下三方面:第一,微觀結構的表征,到目前為止,還沒有找到合適的結構參量、發展相應的理論方法來描述非晶合金和合金液體的微觀結構特征[1];第二,合金液體的復雜動力學,在快速冷卻合金液體、制備非晶合金的過程中,液體的黏度急劇增大十幾個數量級,然而,黏度急劇變化的微觀結構起源仍然是科學難題[2?7];此外,在冷卻過程中,合金液體還表現出復雜的動力學轉變(dynamic crossover),包括結構弛豫時間由Arrhenius行為轉變為non-Arrhenius行為,擴散系數與黏度的關系由Stokes-Einstein(SE)關系轉變為Fractional SE關系,動力學由均勻性轉變為非均勻性,這些動力學轉變的微觀機理仍不清楚,它們之間的因果關系更是存在很大的爭議[7];這些動力學轉變都發生在玻璃轉變之前,因此探索它們的微觀機理及相互關系對最終理解液體的性質和玻璃轉變至關重要;第三,非晶合金的形變機理,非晶合金結構無序,沒有晶體中的缺陷或位錯等,非晶合金如何耗散外力作用而發生形變、其微觀結構起源等仍是關鍵難題,嚴重制約著非晶合金材料的研發和工程應用[8?10].

到目前為止,大量的研究試圖采用原子短程序(原子團簇)來理解非晶合金和合金液體的微觀結構及性能關系[1].然而,原子短程序的種類繁多,不同非晶合金或合金液體中的短程序種類和含量也各不相同,用原子短程序描述其微觀結構及性能關系缺乏統一性和普適性,無法給出簡單、清晰的物理圖像.找到一個簡單、普適的結構參量成為解決非晶合金和合金液體的結構表征難題、建立結構與性能關系的關鍵[11,12]

本文簡要回顧了從20世紀30年代至今,有關合金液體和非晶合金微觀結構的理論、實驗和模擬研究,總結了簡單液體結構的早期研究中所提出的二十面體短程序和無規密堆模型中局域五次對稱性的重要性,以及80年代以來研究人員為尋找合金液體和非晶合金中的局域五次對稱性在理論和實驗等方面所做出的努力.本文最后簡單總結了近幾年采用局域五次對稱性為結構參量定量描述合金液體及非晶合金結構和性能關系的主要研究進展.

2 簡單液體結構的早期研究

對液體結構的認識可以追溯到20世紀30年代,研究人員通過衍射方法或者構建模型,希望能夠得到液體中分子的排列規律,從而了解液體的微觀結構并解釋液體的各種性質.早在20世紀30年代,Bernal和Fowler[13]研究了水和離子溶液,并認為水的結構是類似于二氧化硅中的四面體結構的混合物,根據這個結構模型,可以估算出不同溫度下水的X射線衍射結構因子.為了認識簡單液體,如合金液體和惰性氣體液體的微觀結構,Bernal[14]將水的四面體結構模型應用到密堆的單原子液體,試圖通過配位數描述簡單液體的結構.后來,Bernal[15]自己也認識到該模型太過人為化,并沒有得到任何定量的結果.之后的很長時間內,Bernal的注意力更多地集中于蛋白質和病毒,還有戰爭.在這期間,研究人員對液體結構的研究付出了很大的努力,形成以下三種觀點.Born和Green[16]從高密度氣體理論出發,研究液體中分子之間的相互作用勢,先考慮兩個分子對,再處理三個,依次類推.該模型不可避免地要處理非常復雜的數學公式,卻無法得到非常有用的結果.另一方面,Kirkwood等[17]把液體看成是具有非常多缺陷的固體,也就是從固體中抽取一部分原子,該模型也被稱為液體的孔洞理論(hole theory of liquids).當液體的密度變化不大時,一般小于相應晶體的15%,該模型能夠對液體的動能和勢能給出近似正確的結果.然而,該模型不能正確描述液體的熵以及與熵相關的其他性質.第三種模型是以Eyring[18]為代表,他們將液體看成是由微小晶粒構成的,晶粒內部是有序的,而晶粒之間是無序的或者存在缺陷或位錯.該模型介于上面兩個模型之間.

與此同時,實驗上對簡單液體的研究也取得了很大的進展.20世紀40年代,Turnbull[19]發現不僅僅是二氧化硅和甘油,簡單金屬液體也可以被過冷到熔點以下較低的溫度而不發生晶化.這使得人們意識到液體結構也許跟晶體有本質的區別.X射線衍射數據表明簡單液體中原子的最近鄰配位數與相應晶體結構的非常接近,很容易晶化,這可能是研究人員認為簡單液體不能被過冷的主要原因.基于Turnbull的實驗結果,Frank[20]認為,這種理論解釋有可能是錯的.Frank考慮了12個原子同時圍繞一個原子的堆垛方式,除了熟知的面心立方和六角密排堆垛方式外,還有一種堆垛方式就是正二十面體.前兩種堆垛形成了晶體元胞,具有晶體對稱性,可以重復并充滿整個三維空間.對于正二十面體,該結構包含五次對稱軸,不具有晶體對稱性,因此不能連續擴展而充滿整個三維空間.如果采用Lennard-Jones兩體勢作為原子間相互作用勢,Frank發現正二十面體的結合能比面心立方和六角密排大8.4%.也就是說,盡管簡單液體的配位數與晶體很接近,但堆垛方式可能有很大差別.因此,Frank認為十二個原子圍繞中心原子以二十面體方式堆垛形成的結構單元可能在簡單液體中普遍存在,并以此來理解簡單液體的過冷以及晶化的形核率.這可能是第一次將五次對稱性引入到簡單液體的結構中.后來Bernal[21]提出硬球無規密堆模型來研究簡單液體的結構,通過幾何方法研究結構特征,并發現局域五次對稱性廣泛分布于簡單液體中.Hoare等[22]進一步研究了顆粒團簇的能量,發現包含上百個原子的顆粒仍然傾向于按照非晶體方式排列,如二十面體方式.他們猜想在過冷液體中這些非晶顆粒的尺寸隨溫度降低而增大直到發生玻璃轉變,形成幾何阻挫效應,從而將五次對稱性與玻璃轉變聯系起來.

20世紀50年代末,Bernal重新開始關注簡單液體結構的研究.Bernal[15]對前面提到的三種液體結構模型都不滿意,他認為,這些模型都做了很多的近似,但是只能解釋液體的某些特定的性質.例如,基于晶體結構的液體模型,盡管可以對能量給出很好的描述,然而由于模型中存在一定的長程有序,不能很好地符合液體的X射線衍射結果.Bernal[21]于1959年提出了新的液體結構模型——硬球無規密堆模型.Bernal把構成液體的原子或分子看成大小相同的硬球,并且硬球是不可壓縮的,即硬球如果相互不接觸,相互作用為零,一旦接觸,勢能則為無窮大.Bernal認為簡單液體的結構可看作是均勻連續的、致密填充的、混亂無規的原子球的聚集,其中不包含任何晶體結構區域,并且不存在可以容納一個硬球的孔洞.在該模型中,Bernal特別關注了無規聚集的原子或者分子的近鄰關系.他從Frank和Kasper[23]引入多面體來表征復雜合金的結構研究中得到啟發,意識到無序的單原子液體結構也可以采用類似的幾何分析方法[15].因此,Bernal采用多面體方法分析無規密堆模型的原子結構,并認為液體的性質可以通過不規則多面體的堆積來認識和理解,而近鄰多面體的無規性是液體區別于晶體的關鍵因素.Bernal最初利用橡膠球和輻條構建了無規模型結構,輻條長度在2.75和4英寸之間,盡可能地使構建的結構無規則[21],如圖1所示.Bernal意識到分子或原子在三維空間的無規密堆與相同的球相切形成的各種多面體是一致的,并試圖通過數學和模型來描述這種無規特征.

圖1 Bernal利用橡膠球和輻條構建的無規結構模型[21]Fig.1. Bernal’s ball-and-spoke model of irregular structure[21].

Bernal[21]利用多面體幾何分析方法研究無規密堆結構,發現了32種多面體,并注意到在這些多面體中,五邊形的面占絕對主導.這些多面體中包含〈0,0,12,0〉, 〈0,1,10,2〉, 〈0,2,8,2〉, 〈0,3,6,4〉等已經很熟悉的多面體類型.更重要的是,他發現五邊形的面分布很廣,并且認為這是硬球無規聚集的本征幾何特征.在規則的三維原子排列中,對稱性僅限于2,3,4和6,而五邊形的排列只能出現在復雜的無序結構中,如合金液體.Bernal[21]還認為,無規密堆與五邊形的排列有著緊密關聯.但是,由于缺乏足夠的幾何統計,Bernal無法提供相應的證據.但是,他已經意識到五次對稱性在簡單液體的結構中起著非常重要的作用,并且與液體的性質也緊密關聯,他認為簡單液體中原子以五次對稱的方式排列一定對應著液體的流動性.

Bernal的無規密堆模型能詳細描述簡單液體中粒子的幾何平均位置,所得到的徑向分布函數能與實驗結果很好地吻合.更重要的是該模型能夠通過計算機模擬實現,有效而便捷地對比真實液體和非晶體系,并與分子動力學模擬有效銜接.在此基礎上,Bernal[24]還提出理想液體結構模型,認為理想液體結構中包含五種多面體孔洞,多面體孔洞的頂點為球心位置,各面是等邊三角形.各種多面體靠這些三角形連接,通常稱為Bernal孔洞,分別是四面體、八面體、三角棱柱、阿基米德反棱柱和四角十二面體.在無規密堆模型中,四面體結構占73%.四面體多、八面體少是非晶無序結構的重要特征.四面體是一種短程的、局域的密堆結構.此外,后三種孔洞的存在阻止了任何長程序的形成.Bernal也意識到,即使在最無規的結構中也有可能存在由四面體相互連接構成的區域.這些區域的密度可能比規則密排結構的要高,但它們通常不是晶體,而是非對稱的或是包含五次對稱性[24].這些構型不能重復充滿整個三維空間,因此也不能作為晶體核.這對當時理解過冷液體的形核和晶體生長等非常重要.可以看出,Bernal當時已經意識到簡單液體結構中五次對稱性的重要性.

因此,在簡單液體結構的早期研究中,無論是Frank的二十面體短程序的猜想,還是Bernal的無規密堆模型,其核心內容是五次對稱性.對于二十面體短程序,五次對稱性是其本征性質.而在無規密堆模型中,五次對稱性并不是顯而易見的,而是模型的其中一個結果,表明了簡單液體結構的幾何統計性質,并且Bernal已經意識到該性質與液體結構的無規性、流動性等相關聯.

3 尋找簡單液體中的局域五次對稱性

Frank從13個原子密堆形成的短程序結構出發,猜想二十面體可能是簡單液體中的結構單元.由于二十面體短程序具有五次對稱性,能夠很好地理解金屬液體過冷的微觀機理,因此研究人員一直試圖從實驗和理論方面證明簡單液體中存在二十面體結構單元,從而證明五次對稱性的存在.1960年,加州理工學院Duwez教授等[25]制備出金屬玻璃,也稱非晶合金,更激發了研究人員對過冷液體和金屬玻璃微觀結構的興趣和廣泛關注,并希望從微觀結構的演化理解合金過冷液體的動力學性質和玻璃轉變機理.然而,對于無序體系,散射實驗只能得到平均的結構信息,無法獲得微觀結構的信息,因此也無法明確二十面體結構單元的存在.研究人員更多地從理論出發,發展各種結構分析方法,研究簡單液體和合金過冷液體的微觀結構特征,尋找具有五次對稱性的二十面體.

Steinhardt等[26,27]首先從局域結構的對稱性出發,提出了bond-orientational order(BOO)參數,系統分析了面心立方、六角密堆和正二十面體結構單元的不同BOO所對應的數值.考慮一個中心原子和其近鄰原子組成的結構單元,中心原子i與近鄰原子j形成的鍵可以用球諧函數Ylm(θ,φ)表示如下:

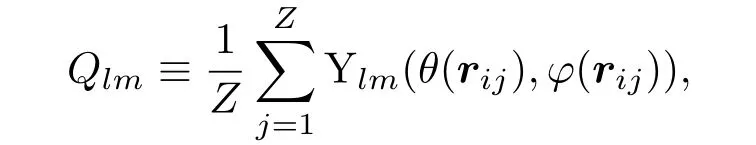
這里rij=rj?ri,Z代表中心原子i的近鄰數或配位數.由于Qlm對于特定的l、不同的m相應的Qlm變化較大,通常考慮旋轉不變性組合,BOO參數可以表示為

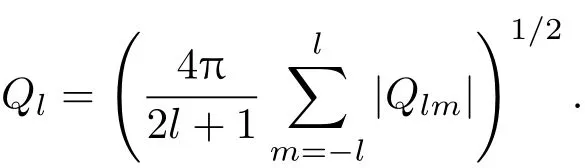
相應的三階不變量可以表示為

這樣,可以計算不同結構的BOO參數,從而表征這些結構單元的對稱性.圖2給出了二十面體、面心立方、六角密排和體心立方結構單元的Ql,可以看出不同結構單元的Ql不盡相同,原則上可以通過Ql值對這些結構單元加以區分.

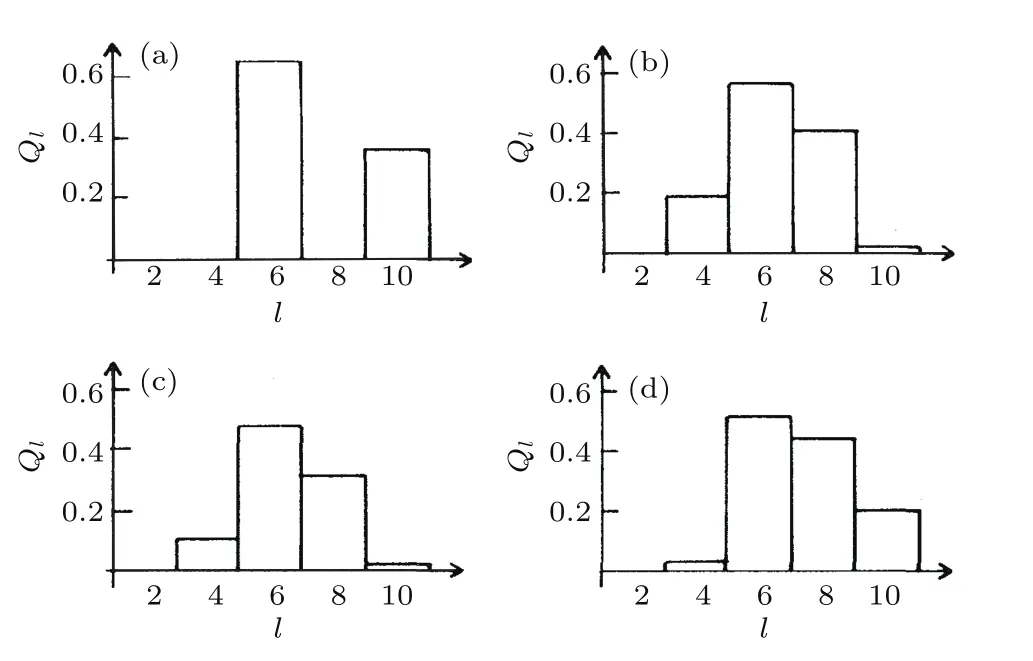
圖2 二十面體(a)、面心立方(b)、六角密排(c)和體心立方(d)結構的Ql值,其中l=2,4,6,8,10[27]Fig.2.Ql(l=2,4,6,8,10)values of iocsahedron(a),face-centered cubic structure(b),hexagonal closedpacked structure(c),and body-centered cubic structure(d),respectively[27].

對于fcc,bcc,hcp和icosahedron而言,6值分別為?0.01316,0.01316,?0.01244和?0.16975.可以看出,BOO參數6可以將五次對稱性與晶體對稱性完全區分開.因此,該參數被廣泛用來分析合金液體和金屬玻璃中原子短程序的局域對稱性.Steinhardt等[26,27]利用他們所提出的BOO參量分析了Lennard-Jones(LJ)過冷液體的鍵向序,發現當溫度低于熔點溫度10%左右時,長程鍵向序漲落出現,并且以二十面體鍵向序為主導,表明了過冷液體中二十面體的存在.

1987年,Honeycutt和Andersen提出了新的表征合金液體中原子的堆積方式及特征,通常被稱為Honeycutt-Andersen(HA)指數[28].HA指數用來描述兩個鍵對原子及其共同近鄰原子之間的多體關聯,通常用ijkl四個指標表征堆垛方式.i表示該鍵對原子對是否為最近鄰原子,i=1表示近鄰,i=2表示非近鄰,通常只考慮兩個鍵對原子為近鄰的情況;j表示兩個鍵對原子共有的最近鄰原子數;k表示j個共有近鄰原子中所形成的鍵對數目;l則用來區分ijk指標相同、但所形成的鍵對方式不同的拓撲結構.為了簡單起見,通常的分析中不區分l這個指標,也就是用ijk三個指標來表征.因此,155指數代表了這兩個鍵對原子的5個共同最近鄰原子形成一個五邊形的環,而154或者153指數表示在這5個共同最近鄰原子其中兩個或三個原子之間沒有成鍵.此外,166,165,144,142這些HA指數分別代表了晶體中的面心立方、體心立方和六角密堆結構中的鍵對特征.因此,HA指數可以表征局域原子堆垛和對稱性特征,也被用來研究液體在冷卻過程中微觀結構的演化以及玻璃轉變機理等.Jonsson和Andersen[29]利用HA指數研究了LJ液體在玻璃轉變過程中微觀結構的演化,發現隨著溫度的降低,以155指數為代表的局域五次對稱性變得越來越多,并且通過相互貫穿或面連接的方式發生逾滲,表明了局域五次對稱性的演化與玻璃轉變的關聯性.

另一方面,研究人員通過發展新的實驗技術探測液體和玻璃結構中的局域五次對稱性,從而從實驗上驗證Frank的猜想,驗證液體中五次對稱性的存在.2000年,Reichert等[30,31]發展了對固液界面上液體結構敏感的totally internally re fl ected X-ray技術,克服了當前散射實驗技術的限制,通過研究Si(111)表面上Pb液滴的結構,觀測到了Pb液體中的局域五次對稱性.Wochner等[32]發展了新的X射線cross correlation analysis,該技術能夠分辨出無序體系中隱含的局域結構序.通過研究膠體玻璃,他們發現不同的局域對稱性對應著不同的波矢值,而這些波矢值并不對應著無序結構的結構因子峰位.在這些局域對稱性中,分布最多的就是局域五次對稱性,從而表明在膠體玻璃中存在局域五次對稱性.

除了發展新的實驗表征技術和理論分析方法,研究人員還結合常規實驗表征技術和模擬方法,尋找過冷液體和非晶合金中的二十面體短程序.Di Cicco等[33]結合X射線吸收邊數據和逆蒙特卡羅方法,利用逆蒙特卡羅方法擬合實驗數據,得到Cu過冷液體的原子構型,并采用BOO方法分析了Cu過冷液體的6分布,從而發現在Cu過冷液體中有一部分局域結構是很接近于二十面體構型,表明簡單過冷液體或合金過冷液體中存在二十面體構型.Luo等[34]測量了Ni-Ag金屬玻璃的擴展X射線吸收精細結構和X射線吸收近邊結構,并通過逆蒙特卡羅方法擬合這些實驗測量數據得到原子構型.他們通過分析NiAg金屬玻璃中共同近鄰原子對,發現NiAg金屬玻璃中存在極高程度的二十面體短程序.這些研究結果都表明合金過冷液體或金屬玻璃中都存在一定程度的二十面體短程序.

Kelton長期致力于合金液體中二十面體短程序及其與玻璃轉變、晶化等關聯的實驗研究.2003年Kelton等[35]采用X射線技術研究了靜電懸浮的金屬液體,觀測到了在降溫過程中晶化的形核勢壘與增長的二十面體短程序之間存在緊密關聯.Kelton等[36]還通過對比TiZrNi合金的單晶相,二十面體準晶相和多四面體相的約化過冷度,發現液體形成準晶相的過冷度較小,表明TiZrNi合金過冷液體中的局域結構是二十面體短程序,與Frank的猜想是一致的.

2013年,陳明偉研究組[37]通過發展埃尺度電子束衍射技術并結合計算機模擬,觀測到非晶合金中的二十面體以及其他類型的原子短程序,發現所觀測到的二十面體短程序都發生了扭曲,從實驗上給出了二十面體在非晶合金中存在的直接證據.不僅如此,他們還發現這些扭曲的二十面體短程序不僅僅包含五次對稱性,還包含部分fcc晶體對稱,并且其他類型的原子短程序也具有類似的結構特征.該結果不僅給出了非晶合金中存在二十面體短程序的證據,還對扭曲的二十面體短程序以及其他類型短程序的對稱性特征給出了新的認識.

以上這些理論和實驗結果都直接或者間接地表明在簡單液體、合金液體或者非晶合金中二十面體短程序或者五次對稱性的存在,一方面驗證了Frank的猜想,另一方面也表明二十面體或者五次對稱性在這些體系中起著非常重要的作用.

4 二十面體短程序與性能的關聯

研究人員一方面通過發展實驗技術和理論分析方法尋找液體和玻璃中二十面體短程序存在的證據,從而證明合金液體和玻璃態中存在五次對稱性;另一方面,在凝聚態物理和材料科學領域,建立材料的結構和性能之間的關系對理解材料的物理、化學、力學性質等至關重要.然而,合金液體和玻璃態的結構無序,不存在晶體結構中的原胞或晶胞,如何描述其微觀結構成為建立結構和性能關系的關鍵.二十面體短程序這樣一個極具代表性的微觀結構單元很自然地成為人們關注的焦點,大量的研究試圖從二十面體短程序出發理解液體的動力學、力學性質、玻璃轉變的結構起源以及合金玻璃形成能力的微觀機理等[1,38?50].Ma等在這方面做了大量系統的研究工作.他們采用Voronoi空間分割法研究了各種原子短程序隨溫度、組分以及外力作用的演化,探討了各種原子短程序與非晶合金和合金液體動力學、力學以及玻璃形成能力之間的關聯性.詳見Cheng和Ma[1]于2010年發表在《Prog.Mater.Sci.》的綜述文章.可以看出,二十面體短程序在合金液體的玻璃轉變、動力學演化、非晶合金的形變和晶化以及玻璃形成能力等扮演著非常重要的角色.然而,在表征二十面體短程序及其與性能關聯的研究中,研究人員更多地從結構短程序的角度出發,二十面體短程序作為一類特殊的結構單元,其幾何構型和密堆性質受到更多的關注,也更容易與非晶合金和合金液體的微觀結構特征、動力學和力學等性能之間建立直觀的聯系.然而,大量的研究也表明,除了二十面體短程序,其他一些含量較多的原子短程序在玻璃轉變、形變、玻璃形成能力等也扮演著重要的角色[51?57].由于這些原子短程序構型各異,與非晶合金和合金液體的性能關聯行為也不盡相同,如何理解各種不同原子短程序與性能的關聯性并沒有統一的認識.這也是從原子短程序出發建立非晶合金和合金液體的結構和性能的關系所面臨的問題和困難.此外,如果僅僅考慮二十面體短程序,只能從定性上理解結構和性能的關系,而不能建立定量描述[58].

Ma等[59]仔細分析了非晶合金中不同構型的原子短程序參與準局域軟模的程度,將不同構型的原子短程序進行分類,那些傾向于對軟模有貢獻的原子短程序定義為geometrically unfavored motifs(GUMs),而那些對軟模貢獻很小的原子短程序定義為geometrically favored clusters(GFCs).這樣,可以通過軟模將不同構型的原子短程序統一起來.可以看出二十面體短程序和Kasper多面體短程序屬于GFCs,而GUMs則包含了除二十面體和Kasper短程序之外的多種原子短程序.這樣在一定程度上解決了短程序的多樣性以及與性能關聯性不明確的問題.然而,GFCs的種類和含量隨著體系的不同有明顯的差異,GUMs所包含的原子短程序類型也隨體系發生變化.因此,從原子短程序出發所面臨的問題仍然存在.

Frank[20]當時提出二十面體短程序,強調的是其五次對稱性的屬性.Bernal[21]也意識到五次對稱性與無序密堆之間有著密切的關聯.大量的研究表明了二十面體的重要性,其實更本質地反映了局域五次對稱性在合金液體和玻璃態中的關鍵作用.從這個意義上講,僅僅關注二十面體短程序是不夠的,因為除了二十面體短程序之外,其他各種短程序也包含不同程度的五次對稱性,正如Bernal[21]當年指出簡單液體的多面體中,五邊形的面占絕對主導.

5 原子短程序的共同特征:局域五次對稱性

盡管合金液體和金屬玻璃的微觀結構包含了多種多樣的原子短程序,但是不同原子短程序有著共同的特征,那就是都具有局域五次對稱性,只是不同原子短程序中的局域五次對稱性的程度不同,這一點可以從BOO參量和HA指數的分析中可以看出.在BOO參量中,正二十面體結構的6值是?0.1697,而面心立方、體心立方等晶體結構的數值在0附近.在合金液體和金屬玻璃中,6有著非常寬的分布[33,37,60],從?0.17到0.15,表明更多的原子短程序既不是完全的晶體對稱,也不是完全的五次對稱,而是兼而有之.HA指數考慮的一對近鄰原子及其共同近鄰原子的堆垛,反映了該HA鍵對的局域對稱性.如果考慮原子短程序的中心原子和其中一個近鄰原子組成的近鄰原子對及其共同近鄰原子,那么原子短程序可以拆分成多個HA鍵對,每一個鍵對反映了中心原子與其不同的近鄰原子堆垛方式,表明原子短程序包含了五次對稱等不同類型的局域對稱性.如果說五次對稱性是合金液體和玻璃態的屬性,那么除二十面體以外的原子短程序中的局域五次對稱性也應該考慮進來.Voronoi空間分割法把合金液體和金屬玻璃的結構分割成以每個原子為中心的多面體,從幾何構型上對局域原子短程序進行表征和分類,并通過Voronoi指數來標識Voronoi多面體[61,62].例如二十面體短程序可以用〈0,0,12,0〉表征,表示二十面體的Voronoi多面體包含12個五邊形的面,而沒有其他類型的面.盡管Voronoi多面體指數反映了該類原子短程序的局域對稱性信息,但是人們更多地從幾何構型特征和短程序的角度出發去研究Voronoi多面體的分布及其對動力學、力學等性質的影響,而忽略了Voronoi多面體的局域對稱性.

事實上,已經有研究在Voronoi多面體分析基礎上,考察了組成多面體的不同類型的面,如三邊形、四邊形、五邊形、六邊形,在玻璃轉變和形變過程中的演化行為[63,64].可以看出反映五次對稱的五邊形的含量隨溫度降低而增加,隨著應變的增大而減少.相反,反映晶體對稱的三邊形、四邊形和六邊形的含量隨溫度的降低而減少,隨著應變的增大而增大,反映了五次對稱性的特殊性.然而,這樣的分析只是反映了整個系統五次對稱性的統計平均信息,而沒有更深入地分析原子短程序的局域五次對稱性.大量的實驗和理論研究表明,局域原子結構的信息更能夠清晰地反映合金液體和玻璃態的結構特征、動力學非均勻性、弛豫動力學以及形變等與微觀結構的關聯性,從而有助于深入理解玻璃轉變、形變以及玻璃形成能力等的微觀機理.

陳明偉等[37]通過發展埃尺度電子束衍射技術觀測到非晶合金中的二十面體結構都發生了扭曲,這樣的二十面體短程序不僅僅包含五次對稱性,還包含部分的fcc晶體對稱.這些結果表明了即使對于Voronoi指數為〈0,0,12,0〉的二十面體短程序,在非晶合金中的構型也是多種多樣,而其共同的特征是五次對稱性.不僅如此,其他類型的原子短程序也具有類似的結構特征:既包含五次對稱性也包含部分晶體對稱性.該實驗證實了合金液體和金屬玻璃結構中各種各樣的原子短程序的共同特征就是局域對稱性,同時也表明了原子短程序中不同的局域對稱性是幾何阻挫的起源,導致玻璃轉變的發生[37].

Xi等[65,66]認為局域結構在玻璃的形成和性能等扮演著非常重要的角色.除了局域結構的拓撲短程序,局域原子對稱性是另一個重要性質,但是人們對此卻沒有深入的認識.他們發現隨著Co的微量摻雜,CeAlCuCo合金的玻璃形成能力迅速增強,同時他們利用核磁共振技術觀測到該金屬玻璃體系中Al原子周圍環境的局域原子對稱性也急劇增強[65],表明了局域原子對稱性對合金的玻璃形成能力起著非常重要的作用.

不僅在合金液體和非晶合金中,五次對稱性在顆粒物質、膠體玻璃等也廣泛存在,并且在結構阻挫、晶化、動力學變慢等起著非常關鍵的作用,與液體的脆度、玻色峰等也密切關聯[67?70].

6 原子短程序中局域五次對稱性的定量表征

可以看出,局域五次對稱性是合金液體和金屬玻璃微觀結構的本征特性,是普遍存在的.如果能夠對原子短程序的局域五次對稱性進行定量表征,就可以從這個普適的結構參量出發探索合金液體和金屬玻璃的結構與性能的關聯性.Feng等提出一個簡單有效的表征方法.基于Voronoi多面體分析,Voronoi多面體可以采用其含有的三邊形、四邊形、五邊形和六邊形面的個數來表征.這里五邊形的面可以認為代表著五次對稱,而其他面則可以粗略地認為具有部分晶體對稱.對于每一種多面體,其中五邊形面的含量可以用來表征該原子短程序中的五次對稱性.

首先定義Voronoi多面體中各種面的含量[58,71]

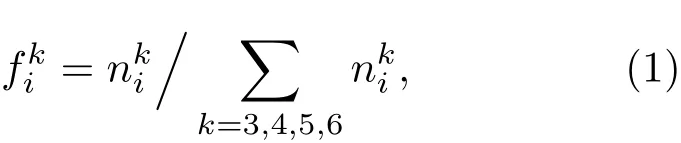
根據上式,各種類型原子短程序中的五次對稱性的含量就可以定量計算. 對于晶體中FCC,BCC結構,其Voronoi指數分別為〈0,12,0,0〉, 〈0,6,0,8〉, 因此, 局域五次對稱性含量的值都為0;而二十面體〈0,0,12,0〉的局域五次對稱性含量的值為1;再如,非晶中Voronoi指數為〈0,2,8,2〉的多面體,其局域五次對稱性含量的值為0.67.根據方程(2),能夠從原子短程序的局域對稱性特征上將合金液體和金屬玻璃中多種多樣的原子短程序統一描述出來.此外,合金液體或金屬玻璃結構的平均五次對稱性可以表示為

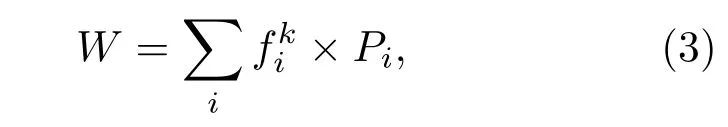
這里Pi表示Voronoi多面體i的含量.以上對局域五次對稱性的定義較簡單、粗糙,但是基本反映了局域原子短程序中的所含有的五次對稱的程度,因此可以用來探索合金液體和金屬玻璃的結構與性能的關系.

Hu等[58]發現,合金液體的平均五次對稱性在玻璃轉變過程迅速增強.不同合金液體在過冷液相區的平均五次對稱性隨溫度的演化行為很類似,但是在發生玻璃轉變形成金屬玻璃后,不同體系中的平均局域五次對稱性是不同的.這一性質有可能與合金的玻璃形成能力密切相關.可以看出,玻璃形成能力越強的合金,其金屬玻璃中的平均五次對稱性越高.局域五次對稱性與玻璃形成能力的關聯性還有待于進一步深入研究.他們還建立了合金液體的黏度和結構弛豫時間與平均五次對稱性之間的定量關系[58],

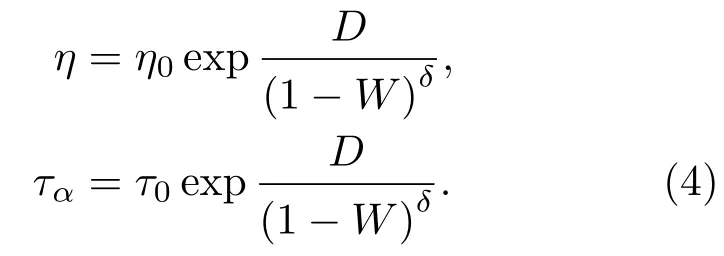
該方程與Vogel-Tammann-Fulcher(VTF)方程形式上一致,所不同的是方程(4)包含了一個描述五次對稱性的結構參量,建立了合金液體的結構和黏度和弛豫時間的關系,從微觀結構的演化給出了在玻璃轉變過程中黏度或弛豫時間.從圖3中可以明顯看出方程(4)很好地描述了不同合金液體的結構弛豫時間與平均五次對稱性行為,表明局域五次對稱性參量反映了合金液體微觀結構和動力學演化的本質,具有普遍性.Lagogianni等[72]將局域五次對稱性與原子間相互作用勢聯系起來,從而對合金液體的脆度有了新的認識.

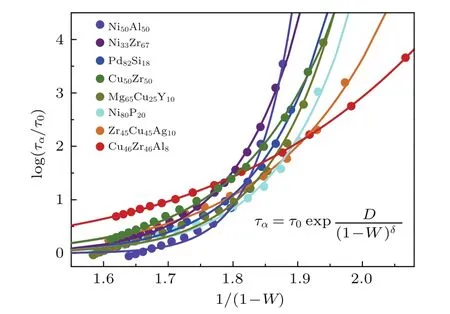
圖3 不同合金液體的結構弛豫時間與平均五次對稱性的關系,散點為分子動力學模擬結果,實線為方程(4)的擬合結果[58]Fig.3.Relation between structure parameter W and relaxation time. The dotted and solid curves are simulation data and the fi ttings with Eq.(4),respectively[58].

方程(4)與著名的過冷液體動力學理論—–Adam-Gibbs理論提供了微觀結構的演化機理.20世紀60年代Adam和Gibbs建立了過冷液體黏度η與構型熵Sc之間的關系η =Aexp(B/TSc)[73].根據Adam-Gibbs公式和方程(4),可以建立構型熵與合金液體平均五次對稱性之間的關系:Sc～ (1?W)δ/T.可以看出,當W →1,構型熵Sc將趨于0,這意味著理想玻璃的形成.以上結果意味著理想玻璃結構應只具有五次對稱性,并且其構型熵為0.該結果還有待于進一步的實驗驗證.從以上分析可以看出,局域結構五次對稱性參量為液體的構型熵提供了清晰的物理圖像和微觀結構基礎,從而能夠進行解析理論推導,為實驗和理論進一步探索液體動力學演化奠定了理論基礎.

此外,我們的研究還表明局域五次對稱性與合金熔體中存在的具有一級相變特征的“液體-液體相變”密切相關.Xu等[74]通過高溫核磁共振技術觀測到La50Al35Ni15合金液體在熔點以上溫度存在的具有一級相變特征的“液體-液體相變”.計算機模擬確認了實驗結果,并發現在相變過程中液體的密度并未發生突變,但局域結構五次對稱性卻發生了突變,表明了該“液體-液體相變”是由局域結構五次對稱性為序參量的一級相變[74].這也充分表明在合金液體和金屬玻璃中局域結構五次對稱性的本質特性,對確定合金液體結構和動力學性質、構建液體的理論框架是極其重要的.日本東京大學Tanaka教授[75]提出了兩序參量模型,他認為要理解液體的動力學行為、液體-液體相變以及玻璃轉變機理等,除了密度以外,還需要一個包含局域結構對稱性的序參量.Xu等的模擬和理論分析結果確認了該兩序參量模型中的局域結構對稱性參量與液體的局域五次對稱性相關.

以上結果都是從平均五次對稱性出發理解合金液體的宏觀動力學性質.方程(2)定量地描述了原子短程序中的局域對稱性,因此,還可以用局域五次對稱性表征局域結構特征,從而探索局域五次對稱性與金屬玻璃的結構非均勻性特征、局域化塑性形變的結構起源、合金過冷液體的動力學非均勻性以及Stokes-Einstein(SE)關系失效與微觀結構演化的關聯性等[12,71,76,77].其中的本質是局域五次對稱性較高或較低的原子短程序傾向于聚集在一起,產生空間關聯,形成團簇,并且關聯長度隨溫度的降低而增大,從而影響合金液體和非晶合金的微觀結構、動力學、力學等性質,如圖4所示.可以發現與局域五次對稱性相關的結構關聯長度隨溫度的演化表現出兩個特征行為,對應的兩個溫度點TA和TS恰好與不同動力學轉變溫度相符合[76].當溫度降至TA,合金液體的微觀結構開始產生空間關聯;同時,結構弛豫時間由Arrhenius轉變為non-Arrhenius行為,并且SE關系開始失效.當溫度降至TS,微觀結構的空間關聯達到一個臨界態,此時液體動力學開始表現出非均勻性,擴散系數和黏度的關系開始遵從Fractional SE關系[76].另外,由于局域五次對稱性較高的原子短程序,與其相關的動力學也相對較慢.相反,局域五次對稱性較低的原子短程序的動力學卻相對較快,這樣合金液體的動力學在空間上分布是非均勻的.這種非均勻性隨著溫度的降低而增強,為合金過冷液體的動力學非均勻性提供了新的微觀結構的演化機理[58].更詳細的研究進展可參閱文獻[11,12].可以看出,從局域五次對稱性出發,可以對合金液體的微觀結構和復雜動力學行為、玻璃轉變、非晶合金的微觀結構、變形等給出統一的、簡潔明了的數學描述和物理圖像.

圖4 Cu46Zr46Al8體系中由局域五次對稱性f5≥0.6的原子形成的最大團簇在不同溫度的空間分布(a)2.5Tg;(b)2.0Tg;(c)1.5Tg;(d)0.9Tg(Tg=771 K),團簇包含的原子數分別為32,190,1726和5684[58]Fig.4.Snapshots of the biggest cluster formed by atoms with f5≥0.6 at 2.5Tg(a),2.0Tg(b),1.5Tg(c)and 0.9Tg(d),respectively(Tg=771 K)in Cu46Zr46Al8system.The number of atoms involved in is 32,190,1726 and 5684 for(a)–(d),respectively[58].

7 總結與展望

綜上所述,局域五次對稱性在合金液體和非晶合金中普遍存在,是其本征性質,在Frank和Bernal的簡單液體的結構模型中也體現出了這一點.從Frank的猜想至今,大量的研究致力于證明局域五次對稱性在合金液體和玻璃態的存在,并在理論和實驗方面都得到了印證.同時,局域五次對稱性在描述液體的動力學行為、玻璃轉變以及液體-液體相變和非晶合金的形變等起著非常關鍵的作用,表明了局域五次對稱性的普遍性和有效性.不僅如此,人們可以通過調控合金液體和玻璃態的局域五次對稱性的含量來改變其性質.例如,可以通過微量元素摻雜提高合金體系的五次對稱性的含量,提高體系的玻璃形成能力以及非晶合金的強度[1,65,71,78,79].還可以通過改變溫度或施加外力,改變合金液體和玻璃態中的局域五次對稱性的含量,從而改變其性能.Wu等還發現,團簇的連接程度也可以改變合金液體或玻璃態局域結構的五次對稱性,從而影響系統的動力學和力學性質[50].

要實現對合金液體和非晶合金中局域五次對稱性的調控,首先需要在實驗上實現對局域五次對稱性的定量測量,這方面還存在很大的困難,需要發展新的實驗觀測技術和手段,陳明偉研究組已經取得了實質進展[37].在理論方面,還需要發展更精確的分析表征方法,更好地描述合金液體和玻璃態的局域五次對稱性.目前的定義還很粗糙,對局域五次對稱性的描述也不精確,還存在一定的問題.

到目前為止,人們提出了很多描述合金液體和玻璃態的結構參量,比如BOO參量[26,27]、HA指數[28]、自由體積[80,81]、軟模[82]、結構熵S2[83]、還有局域五次對稱性[58,71].在描述合金液體和非晶合金的結構與性能的關系方面,這些結構參量各有優缺點,系統地分析和對比這些參量之間的相關性可以幫助我們更全面地認識合金液體和非晶合金的性質,優化結構參量,更好地描述無序體系結構與性能的關系.

[1]Cheng Y Q,Ma E 2011 Prog.Mater.Sci.56 379

[2]Royall C P,Williams S R 2015 Phys.Rep.560 1

[3]Ediger MD 2000 Annu.Rev.Phys.Chem.51 99

[4]Andersen H C 2005 Proc.Natl.Acad.Sci.USA 102 6686

[5]Roland C M2008 Soft Matter 4 2316

[6]Mallamace F,Branca C,Corsaro C,Leone N,Spooren J,Chen S H,Stanley H E 2010 Proc.Natl.Acad.Sci.USA 107 22457

[7]Ngai K 2011 Relaxation and Di ff usion in Complex Systems(New York:Springer)pp1–47

[8]Schuh C A,Hufnagel T C,Ramamurty U 2007 Acta Mater.55 4067

[9]Wang W H 2012 Prog.Mater.Sci.57 487

[10]Greer A L,Cheng Y Q,Ma E 2013 Mater.Sci.Eng.R 74 71

[11]Li MZ 2014 J.Mater.Sci.Technol.30 551

[12]Li MZ,Peng H L,Hu Y C,Li F X,Zhang H P,Wang W H 2017 Chin.Phys.B 26 016104

[13]Bernal J D,Fowler R H 1933 J.Chem.Phys.1 515

[14]Bernal J D 1937 Trans.Faraday Soc.33 27

[15]Bernal J D 1964 Proc.Roy.Soc.Lond.A 280 299

[16]Born M,Green H S 1946 Proc.Roy.Soc.A 188 10

[17]Kirkwood J 1939 J.Chem.Phys.7 919

[18]Erying H 1936 J.Chem.Phys.4 283

[19]Turnbull D 1952 J.Chem.Phys.20 411

[20]Frank F C 1952 Proc.R.Soc.Lond.A 215 43

[21]Bernal J D 1959 Nature 183 141

[22]Hoare MR 1976 Ann.N.Y.Acad.Sci.279 186

[23]Frank F C,Kasper J S 1958 Acta Cryst.11 184

[24]Bernal J D 1960 Nature 185 68

[25]Klement W,Willens R H,Duwez P 1960 Nature 187 869

[26]Steinhardt P J,Nelson D R,Ronchetti M1981 Phys.Rev.Lett.47 1297

[27]Steinhardt P J,Nelson D R,Ronchetti M1983 Phys.Rev.B 28 784

[28]Honeycutt J D,Andersen H C 1987 J.Phys.Chem.91 4950

[29]Jonsson H,Andersen H C 1988 Phys.Rev.Lett.60 2295

[30]Reichert H,Klein O,Dosch H,Denk M,Honkimaki V,Lippmann T,Reiter G 2000 Nature 408 839

[31]Spaepen F 2000 Nature 408 781

[32]Wochner P,Gutt C,Autenreth T,Demmer T,Bugaev V,Ortiz A D,Duri A,Zontone F,Grubel G,Dosch H 2009 Proc.Natl.Acad.Sci.USA 106 11511

[33]Cicco A D,Trapananti A,Faggioni S 2003 Phys.Rev.Lett.91 135505

[34]Luo W K,Sheng H W,Alamgir F M,Bai J M,He J H,Ma E 2004 Phys.Rev.Lett.92 145502

[35]Kelton K F,Lee G W,Gangopadhyay A K,Hyers R W,Rathz T J,Rogers J R,Robinson MB,Robinson D S 2003 Phys.Rev.Lett.90 195504

[36]Lee G W,Gangopadhyay A K,Croat T K,Rathz T J,Hyers R W,Rogers J R,Kelton K F 2005 Phys.Rev.B 72 174107

[37]Hirata A,Kang L J,Fujita T,Klumov B,Matsue K,Kotani M,Yavari A R,Chen MW 2013 Science 341 376

[38]Saksl K,Franz H,Jovari P,Klementiev K,Welter E,Ehnes A,Saida J,Inoue A,Jiang J Z 2003 Appl.Phys.Lett.83 3924

[39]Sheng H W,Luo W K,Alamgir F M,Bai J M,Ma E 2006 Nature 439 419

[40]Cheng Y Q,Sheng H W,Ma E 2008 Phys.Rev.B 78 014207

[41]Wang S Y,Wang C Z,Li MZ,Huang L,Ott R T,Kramer MJ,Sordelet D J,Ho K M2008 Phys.Rev.B 78 184204

[42]Li MZ,Wang C Z,Hao S G,Kramer MJ,Ho K M2009 Phys.Rev.B 80 184201

[43]Shen Y T,KiMT H,Gangopadhyay A K,Kelton K F 2009 Phys.Rev.Lett.102 057801

[44]Cheng Y Q,Ma E,Sheng H W 2009 Phys.Rev.Lett.102 245501

[45]Hao S G,Wang C Z,Li MZ,Napolitano R E,Ho K M2011 Phys.Rev.B 84 064203

[46]Wang Q,Liu C T,Yang Y,Dong Y D,Lu J 2011 Phys.Rev.Lett.106 215505

[47]Soklaski R,Nussinov Z,Markow Z,Kelton K F,Yang L 2013 Phys.Rev.B 87 184203

[48]Wu Z W,Li MZ,Wang W H,Liu K X 2013 Phys.Rev.B 88 054202

[49]Zemp J,Celino M,Schonfeld B,Loffler J F 2014 Phys.Rev.B 90 144108

[50]Wu Z W,Li F X,Huo C W,Li MZ,Wang W H,Liu K X 2016 Sci.Rep.6 35967

[51]Qi D W,Wang S 1991 Phys.Rev.B 44 884

[52]Sha Z D,Wu R Q,Lu Y H,Shen L,Yang M,Cai Y Q,Feng Y P,Li Y 2009 J.Appl.Phys.105 043521(R)

[53]Peng H L,Li MZ,Wang W H,Wang C Z,Ho K M2010 Appl.Phys.Lett.96 021901

[54]Huang L,Wang C Z,Hao S G,Kramer MJ,Ho K M2010 Phys.Rev.B 81 014108

[55]Senkov O N,Cheng Y Q,Miracle D B,Barney E R,Hannon A C,Woodward C F 2012 J.Appl.Phys.111 123515

[56]Guan P F,Fujita T,Hirata A,Liu Y H,Chen MW 2012 Phys.Rev.Lett.108 175501

[57]Leocmach M,Tanaka H 2012 Nature Commun.3 974

[58]Hu Y C,Li F X,Li MZ,Bai H Y,Wang W H 2015 Nature Commun.6 8310

[59]Ding J,Patinet S,Falk ML,Cheng Y Q,Ma E 2014 Proc.Natl.Acad.Sci.USA 111 14052

[60]Li MZ,Wang C Z,Mendelev MI.Ho K M2008 Phys.Rev.B 77 184202

[61]Finney J L 1977 Nature 266 309

[62]Borodin V A 1999 Phil.Mag.A 79 1887

[63]Wakeda M,Shibutani Y,Ogata S,Park J 2007 Intermetallics 15 139

[64]Lee J C,Park K W,KiMK H,Fleury E,Lee B J,Wakeda M,Shibutani Y 2007 J.Mater.Res.22 3087

[65]Xi X K,Li L L,Zhang B,Wang W H,Wu Y 2007 Phys.Rev.Lett.99 095501

[66]Sandor MT,Ke H B,Wang W H,Wu Y 2013 J.Phys.Condens.Matter 25 165701

[67]Royall C P,Williams S R,Ohtsuka T,Tanaka H 2008 Nature Mater.7 556

[68]Li J D,Cao Y X,Xia C J,Kou B Q,Xiao X H,Fezzaa K,Wang Y J 2014 Nat.Commun.5 5014

[69]Shintani H,Tanaka H 2008 Nat.Mater.7 870

[70]Shintani H,Tanaka H 2006 Nat.Phys.2 200

[71]Peng H L,Li MZ,Wang W H 2011 Phys.Rev.Lett.106 135503

[72]Lagogianni A E,Krausser J,Evenson Z,Samwer K,Zaccone A 2016 J.Stat.Mech.:Theor.Exp.8 084001

[73]AdaMG,Gibbs J H 1965 J.Chem.Phys.43 139

[74]Xu W,Sandor MT,Yu Y,Ke H B,Zhang H P,Li MZ,Wang W H,Liu L,Wu Y 2015 Nature Commun.6 7696[75]Tanaka H 2012 Eur.Phys.J.E 35 113

[76]Hu Y C,Li F X,Li MZ,Bai H Y,Wang W H 2016 J.Appl.Phys.119 205108

[77]Gao W,Feng S D,Qi L,Zhang S L,Liu R P 2015 Chin.Phys.Lett.32 116101

[78]Lu Z P,Liu C T 2004 J.Mater.Sci.39 3965

[79]Wang W H 2007 Prog.Mater.Sci.52 540

[80]Turnbull D,Cohen MH 1961 J.Chem.Phys.34 120

[81]Spaepen F 1977 Acta Metall.25 407

[82]Widmer-Cooper A,Perry H,Harrowell P,Reichman D R 2008 Nature Phys.4 711

[83]Yang X N,Liu R,Yang MC,Wang W H,Chen K 2016 Phys.Rev.Lett.116 238003

PACS:61.20.Ja,61.25.Mv,64.70.pe,64.70.Q–DOI:10.7498/aps.66.176107

*Project supported by the National Natural Science Foundation of China(Grant No.51631003),the National Basic Research PrograMof China(Grant No.2015CB856800),the Fundamental Research Funds for the Central Universities,and the Research Funds of Renmin University of China(Grant No.16XNLQ01).

?Corresponding author.E-mail:maozhili@ruc.edu.cn

Five-fold local symmetries in metallic liquids and glasses?

Li Mao-Zhi?
(Department of Physics,Renmin University of China,Beijing 100872,China)

1 June 2017;revised manuscript

18 July 2017)

In this article,we review the experimental,theoretical and simulation studies on fi ve-fold local symmetries in metallic liquids and glasses.In the early study on simple liquid structure,it has been realized that fi ve-fold local symmetry plays a key role in irregular structures,supercooling and crystallization of simple liquids.In particular,icosahedral shortrange order,representative of fi ve-fold local symmetry,has attracted much attention.In addition,researches proposed a dense randoMpacking model for simple liquid structure in 1959,and found a wide variety of polyhedra and absolute predominance of pentagonal faces in simple liquids,and also pointed out that pentagonal arrangements can only occur in very complex structures such as some of the alloy structures.Based on the Frank’s hypothesis of icosahedral shortrange order as blocking unit in a simple liquid,a lot of theoretical and experimental e ff orts have been made to con fi rMits existence in simple liquids,metallic liquids and glasses.So far,several theoretical methods have been developed for characterizing local atomic structures in simple liquids,such as bond-orientational order parameter,Honeycutt-Andersen index,and Voronoi tessellation.Although the local atomic symmetries in atomic structures in metallic liquids and glasses can be characterized by these methods and the geometries of the atomic structures in liquids and glasses have received much more attention,an atomic cluster model has been developed for establishing the structure-property relationship in metallic liquid and glass.Due to the diversity of the atomic clusters in both type and population of di ff erent metallic liquids and glasses,the atomic cluster model could not present a simple description of structure-property relationship.Based on the fundamental characteristics of metallic liquids and glasses, fi ve-fold local symmetry,the structure-property relationship in metallic liquids and glasses,such as dynamic crossover,glass transition,liquid-liquid phase transition,and deformation can be well described in simple,quantitative and uni fi ed ways,and therefore a clear physical picture can be provided.All these studies indicate that fi ve-fold local symmetry as a structural parameter is simple,general and e ff ective.

metallic glass,metallic liquid, fi ve-fold local symmetry

10.7498/aps.66.176107

?國家自然科學基金(批準號:51631003)、國家重點基礎研究發展計劃(批準號:2015CB856800)、中央高校基本科研專項資金和中國人民大學科研基金(批準號:16XNLQ01)資助的課題.

?通信作者.E-mail:maozhili@ruc.edu.cn

?2017中國物理學會Chinese Physical Society

http://wulixb.iphy.ac.cn.