小區開放對道路通行的影響

林宇浩+吳毓雙+劉闖

摘要：隨著城市交通網絡壓力的日益增大，研究開放中國傳統的封閉式小區對于道路交通的影響具有現實意義。文章從信號燈處排隊等待時間這個因素來考慮。根據排隊論的思想建立了等待制模型，分析了開放小區對于其周邊道路交通狀況的影響。

關鍵詞：交通流；排隊論；小區開放

一、研究背景

隨著城市交通網絡壓力的日益增大，如何緩解道路交通的壓力成了亟待解決的問題。由于開放小區能否緩解道路交通的壓力，優化道路網結構，提高道路通行能力等問題都不得而知，雖然理論上來說小區開放后，路網密度提高，道路面積增加，通行能力自然會有提升，但有人對這一提議也提出了質疑，認為這與小區面積、位置、外部及內部道路狀況等諸多因素有關，不能一概而論。還有人認為小區開放后，雖然可通行道路增多了，相應地，小區周邊主路上進出小區的交叉路口的車輛也會增多，也可能會影響主路的通行速度。

二、模型的建立和求解

（一）具體的問題背景與車流量規定

1. 問題假定

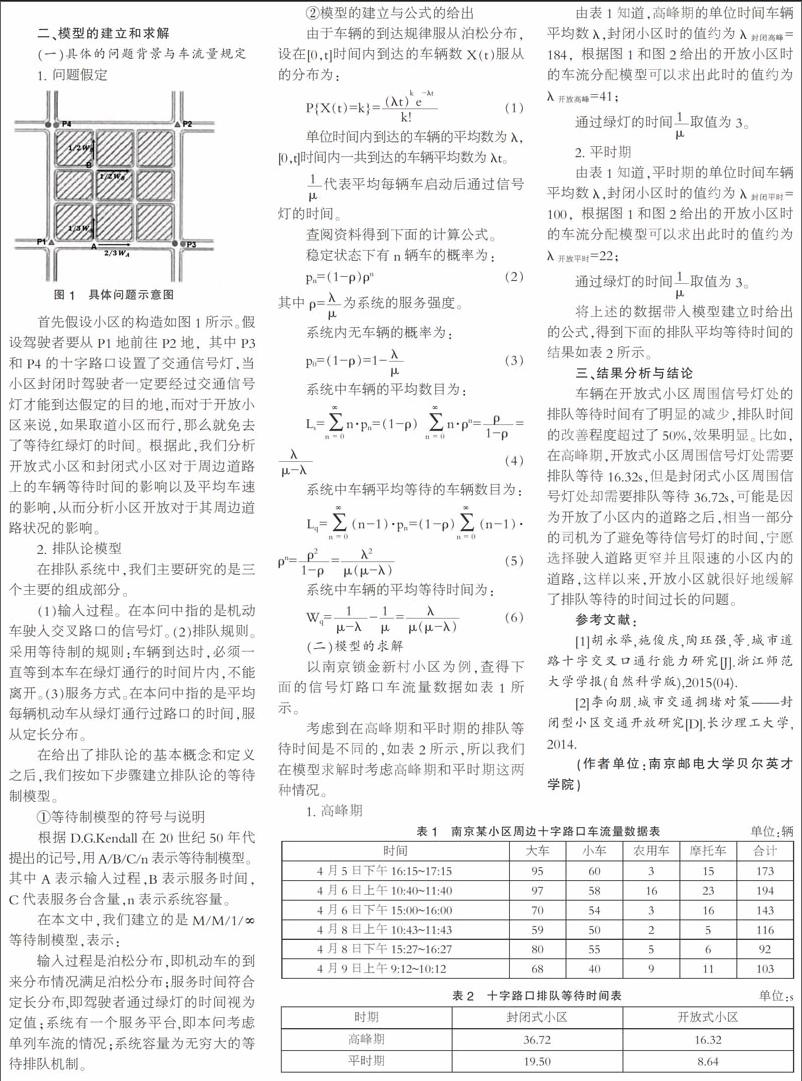
首先假設小區的構造如圖1所示。假設駕駛者要從P1地前往P2地，其中P3和P4的十字路口設置了交通信號燈，當小區封閉時駕駛者一定要經過交通信號燈才能到達假定的目的地，而對于開放小區來說，如果取道小區而行，那么就免去了等待紅綠燈的時間。根據此，我們分析開放式小區和封閉式小區對于周邊道路上的車輛等待時間的影響以及平均車速的影響，從而分析小區開放對于其周邊道路狀況的影響。

2. 排隊論模型

在排隊系統中，我們主要研究的是三個主要的組成部分。

（1）輸入過程。在本問中指的是機動車駛入交叉路口的信號燈。（2）排隊規則。采用等待制的規則：車輛到達時，必須一直等到本車在綠燈通行的時間片內，不能離開。（3）服務方式。在本問中指的是平均每輛機動車從綠燈通行過路口的時間，服從定長分布。

在給出了排隊論的基本概念和定義之后，我們按如下步驟建立排隊論的等待制模型。

根據D.G.Kendall在20世紀50年代提出的記號，用A/B/C/n表示等待制模型。

其中A表示輸入過程，B表示服務時間，C代表服務臺含量，n表示系統容量。

在本文中，我們建立的是M/M/1/∞等待制模型，表示：

輸入過程是泊松分布，即機動車的到來分布情況滿足泊松分布；服務時間符合定長分布，即駕駛者通過綠燈的時間視為定值；系統有一個服務平臺，即本問考慮單列車流的情況；系統容量為無窮大的等待排隊機制。

由于車輛的到達規律服從泊松分布，設在[0，t]時間內到達的車輛數X（t）服從的分布為：

將上述的數據帶入模型建立時給出的公式，得到下面的排隊平均等待時間的結果如表2所示。

三、結果分析與結論

車輛在開放式小區周圍信號燈處的排隊等待時間有了明顯的減少，排隊時間的改善程度超過了50%，效果明顯。比如，在高峰期，開放式小區周圍信號燈處需要排隊等待16.32s，但是封閉式小區周圍信號燈處卻需要排隊等待36.72s，可能是因為開放了小區內的道路之后，相當一部分的司機為了避免等待信號燈的時間，寧愿選擇駛入道路更窄并且限速的小區內的道路，這樣以來，開放小區就很好地緩解了排隊等待的時間過長的問題。

參考文獻：

[1]胡永舉，施俊慶，陶玨強，等.城市道路十字交叉口通行能力研究[J].浙江師范大學學報（自然科學版），2015（04）.

[2]李向朋.城市交通擁堵對策——封閉型小區交通開放研究[D].長沙理工大學，2014.

（作者單位：南京郵電大學貝爾英才學院）endprint