基于Fisher統計量的測試性增長試驗數據相容性檢驗方法

王京，何華鋒，李天梅，徐從啟，楊宗浩，韓聰聰

（1.火箭軍工程大學控制工程系，陜西西安710025；2.解放軍總后勤部建筑工程技術研究所，陜西西安710032）

基于Fisher統計量的測試性增長試驗數據相容性檢驗方法

王京1，何華鋒1，李天梅1，徐從啟2，楊宗浩1，韓聰聰1

（1.火箭軍工程大學控制工程系，陜西西安710025；2.解放軍總后勤部建筑工程技術研究所，陜西西安710032）

在測試性評估過程中，為檢驗測試性增長試驗數據與現場數據的總體一致性，提出一種基于Fisher統計量的相容性檢驗方法。主要針對“小子樣、成敗型”數據，提出順序約束模型完成對試驗數據的增長趨勢檢驗，依據超幾何分布構造Fisher統計量，對相鄰增長階段間連帶關系進行判定，繼而得到增長試驗數據與現場數據總體一致性的相關結論。實例應用表明：在小樣本情況下所提方法能對總體一致性做出合理判定，其可處理的樣本量上限為26，工程實際中，在給定顯著性水平的情況下，應綜合考慮增長成本、結果穩定性、維修改進技術水平等因素的影響，合理安排裝備增長過程中的增長階段數。

測試性評估；相容性檢驗；增長試驗；Fisher統計量

0 引言

測試性是指裝備能及時、準確地確定其狀態并隔離其內部故障的一種設計特性[1-3]。僅通過收集的現場數據對測試性水平進行評估，往往難以獲得高準確度、高置信度的評估結論。因此研發人員通常將除現場數據以外的其他各類信息，如歷史數據、專家經驗數據、增長試驗數據等，也都加以利用[4]。這些數據來自裝備全壽命周期的不同層級、不同階段，具有不同的形式，在統計上具有一定的差異[5-6]。因此在利用多源數據進行評估之前，首先需要對數據進行相容性檢驗，即檢驗其與現場數據的總體一致性，否則基于該數據得到的評估結論不可信[7]。

需要進行相容性檢驗的測試性信息種類繁多，其中很重要的一類就是增長試驗數據。此類數據的獲得貫穿于裝備全壽命周期，反映了裝備的發展進步，但數據量一般較小，屬于“小子樣”的情況，且具有成敗型二值特點[8]。適用于此類數據的檢驗方法，在可靠性領域多有研究。文獻[9-11]認為在分布未知的情況下，Wilcoxon秩和檢驗法比較有效，可直接用于相容性檢驗；文獻[12]提出的K-S檢驗法比秩和檢驗法結果更加嚴謹，可用于開展評估。也有不少文獻沿用顯著性檢驗相關方法，將Konmotopob方法、判別分析方法、矩檢驗法等策略引入相容性檢驗，對樣本進行處理。已有的檢驗方法多是在可靠性背景下提出的，對于測試性增長試驗數據這類規劃性強、增長趨勢明顯的數據，其適用情況說明還不夠明確。且此類數據以“小子樣、成敗型”呈現，通用的檢驗方法對其獨特的數據特征提取不夠明顯，因此有必要針對性地提出相應的相容性檢驗方案。

根據以上研究現狀，結合測試性增長試驗數據的特點，本文提出了基于Fisher統計量[13-15]的非參數相容性檢驗方法。首先利用序化模型對增長試驗各階段進行增長趨勢驗證，然后計算相鄰階段Fisher統計量值，判定其連帶關系，最后給出相應的檢驗結論，并就增長階段和樣本數對檢驗成敗的影響進行討論。

1 增長趨勢驗證

測試性增長試驗是通過試驗和使用，發現裝備或單元存在的問題，并采取改進措施，使故障診斷能力得到提升的一類試驗[16]。目前得到的測試性增長試驗數據為單個增長階段的成敗型試驗數據，其數據量較小，分布參數不固定，屬于“小子樣、異總體”的情況。針對此類數據的特點，研究提出基于Fisher統計量的測試性增長試驗數據相容性檢驗策略。

假設裝備在得到最終評估指標結論之前，經歷了m個增長階段，每個增長階段的故障檢測率水平用qi（i=1，2，…，m）表示，最終裝備的所處階段記作第m+1階段。為完成增長基本任務，當測試性增長試驗的效果良好時，應存在如下順序約束模型：

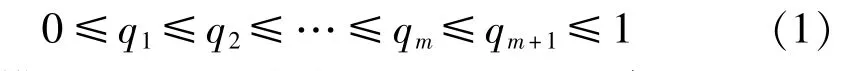
該模型主要用于判斷增長過程是否存在明顯增長趨勢。

2 基于Fisher統計量的相鄰階段連帶關系判定

結合檢驗所需，在連帶關系判定上提出假設H0與其備擇假設H1：

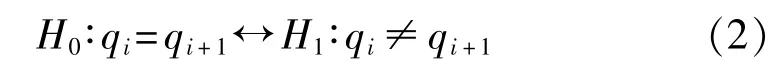
首先，將相鄰階段的成敗型試驗數據寫成列聯表形式，如表1所示。

表1 相鄰階段成敗型試驗數據2×2列聯表

對上表進行分析處理，計算其超幾何分布概率：

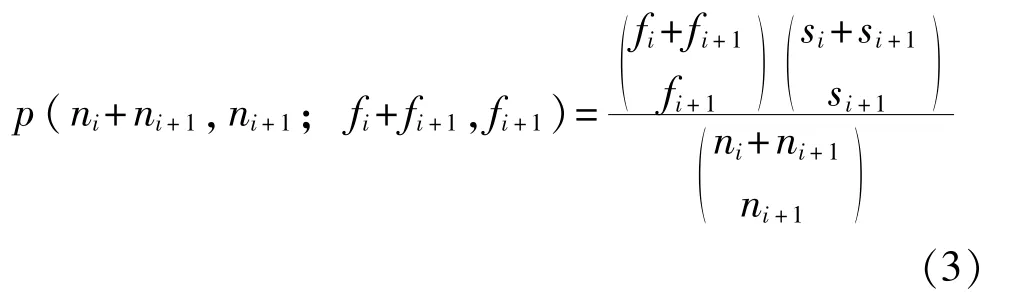
將上表所有排列的超幾何分布概率之和記為P，分下列兩種情形進行討論分析。

1）若fi+1/ni+1〈fi/ni，Fisher統計量用多個階段的超幾何分布概率表示為

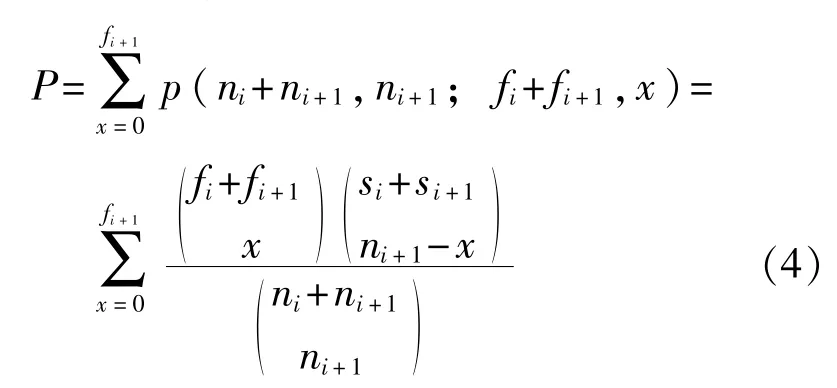
為使式（4）排列計算能夠得到實數范圍內結果，應滿足如下約束：

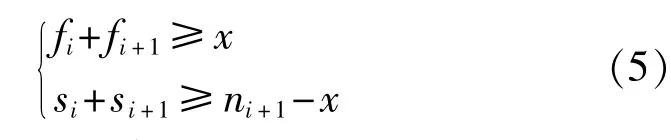
2）若fi+1/ni+1＞fi/ni，則：

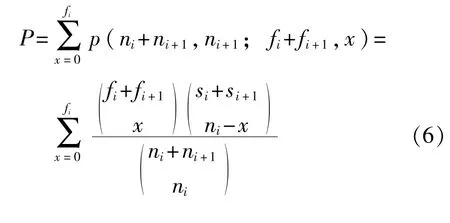
為使式（6）排列計算能夠得到實數范圍內結果，應滿足如下約束：

實際應用中顯著性水平通常取α≤0.2；如果已經證明武器裝備故障檢測水平存在增長，則α可取0.3或0.4，甚至更高[4]。

上述模型主要適用于小子樣情況，通過仿真發現，當樣本數超過26之后，上述模型將不再適用。分析其原因，主要是樣本量增大之后，約束式（5）和式（7）將不再滿足。而且由于排列中涉及到階乘運算，當排列的基數較大時，計算上將比較困難。

在取定α前提下，如果滿足P＞α，表明相鄰階段故障檢測率指標之間沒有顯著的連帶關系，此時接受假設H0；如果P≤α，則接受假設H1，認定相鄰階段故障檢測率指標之間具有明顯的連帶證據，說明存在相互關聯。

當裝備全壽命周期經歷的增長階段較少時，統計到的數據相對較少，不利于對裝備整體狀態和性能的認知，但如果如期完成增長任務，則可說明裝備每次改進較為明顯，能較快達到所要求的水平；當裝備全壽命周期經歷的增長階段較多時（多指經歷了7個以上增長階段），那么收集到的增長試驗數據相對較多，對裝備的認知也更全面，但每次改進幅度相對有限。兩種情況具體優選，應結合研制和改進代價，依據故障注入試驗樣本數多少具體而定。本文結合實例應用，給出了工程建議。

3 實例應用

某型導彈綜合測試模擬訓練系統，在研制過程中，統計到的一個經歷3次大的性能提高。1）聯調初期，第1次通電整體測試，發生5次故障，且都未能成功檢測到。5次故障之后，裝備因故無法繼續運行。2）第2次初樣通電測試，經維修確認共發生7次運行故障，只成功檢測到4次。而后分析原因，對測試裝備進行進一步的改進提高。3）進行樣機完整測試，要求達成所有任務請求，統計到整個運行過程中，一共發生10次故障，有2次未能成功檢測。故障能否被檢測到主要依據于已知故障模式的屏幕提醒。裝備列裝前進行驗證測試，注入12個故障均能做出正確預報。

通過上述過程，統計到增長試驗數據（5，5），（7，4），（10，2）和最終階段試驗結果（n4，f4）=（12，0）。

首先，計算各個增長階段的點估計值，分別為：q1=0，q2=42.86%，q3=80.00%，q4=100%，滿足式（1）所示的順序約束模型，說明各階段間具有明顯增長趨勢。

其次，通過Fisher統計量對相鄰階段間的連帶關系進行判定。在α0=0.2的情況下，將增長數據帶入上述檢驗模型，計算出第1階段到第2階段的Fisher統計量P1≈0.156〈0.2，第2、3階段間Fisher統計量P2=0.145〈0.2，第3階段到最終結果的Fisher統計量值P3=0.195〈0.2，則接受備擇假設H1，說明各相鄰階段間具有顯著的連帶關系。

最后得出結論，該組測試性增長試驗數據通過相容性檢驗。

以Fisher檢驗統計量為指標量值，通過計算機仿真，給出了增長階段數對檢驗通過與否情況的關系，如圖1所示。

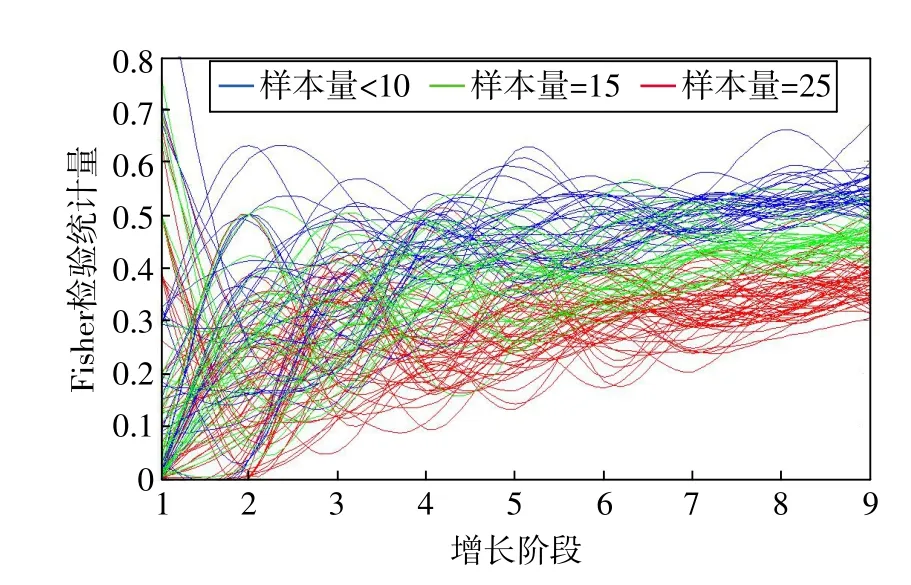
圖1 增長階段、樣本量與Fisher統計量關系圖

由圖可知，當增長階段數較少時，隨著樣本量的增加，Fisher檢驗統計量變化不明顯；而后隨著增長階段數的增加，Fisher檢驗統計量呈緩慢增大趨勢。但隨著增長階段數的增加，當評估的樣本量變大時，Fisher檢驗統計量值就相對變小，更容易通過檢驗。在實際中，樣本量越大，一般得到的結果也越可信，這與上述結論基本一致。因此在條件允許的情況下，盡可能增加樣本量是得到可信結果的首選。

當增長階段數據安排過少時，檢驗結果偶然性太大；增長階段安排過多時，維修改進的成本將增多。因此工程實際中，在給定顯著性水平的情況下，應綜合考慮增長成本、結果穩定性、維修改進技術水平等因素的影響，合理安排裝備增長過程中的增長階段數。

4 結束語

本文研究了一種基于Fisher統計量的測試性增長試驗數據非參數相容性檢驗方法，并得出以下主要結論：

1）提出的Fisher統計量檢驗法針對性較強，主要解決了“小子樣、成敗型”數據的相容性檢驗問題。

2）針對增長試驗數據，結合數據特點，分別對增長趨勢和連帶關系進行判定，檢驗思路更加完整。

3）通過討論分析，驗證了樣本量越充足越容易通過相容性檢驗的結論；具體的增長階段數應結合實際情況進行合理安排。

[1]中國航空工業總公司三○一所.裝備測試性大綱：GJB 2547-1995[S].1996.

[2]田仲，石君友.系統測試性設計分析與驗證[M].北京：北京航空航天大學出版社，2003：173-182.

[3]張偉昆.測試性分析與評估體系的研究[J].國外電子測量技術，2015，34（5）：38-42.

[4]常春賀，楊江平，曹鵬舉.基于研制信息的測試性驗證試驗方案研究[J].航空學報，2012，33（11）：2057-2064.

[5]徐萍，劉松林，李勇.測試性試驗概念及模型研究[J].計算機測量與控制，2006，14（9）：1149-1152.

[6]李天梅.裝備測試性驗證試驗優化設計與綜合評估方法研究[D].長沙：國防科學技術大學，2010.

[7]劉晗，郭波.小子樣產品可靠性Bayes評定中的相容性檢驗方法研究[J].機械設計與制造，2007（5）：165-166.

[8]LI T M，XU C Q，QIU J，et al.The assessment and foundationofbell-shapedtestabilitygrowtheffort functionsdependentsystemtestabilitygrowthmodels based on NHPP[J].Mathematical Problems in Engineering，2015，2015：1-17.

[9]李鵬波，張士峰，蔡洪.導彈仿真試驗結果靜態一致性檢驗及其置信度[J].現代防御技術，1999（6）：31-36.

[10]張湘平，曹國敏.驗前信息與現場子樣的相容性檢驗方法研究[J].飛行器測控學報，2002，21（1）：55-59.

[11]張金槐.多源信息的Bayes融合精度鑒定方法[J].國防科技大學學報，2001，23（3）：93-97.

[12]胡正東，曹淵，張士峰，等.特小子樣試驗下導彈精度評定的Bootstrap方法[J].系統工程與電子技術，2008，30（8）：1493-1497.

[13]茆詩松.統計手冊[M].北京：科學出版社，2003：177-185.

[14]LOVEJJ.Fisherstatistics[C]∥Encyclopediaof Geomagnetism and Paleomagnetism Springer Netherlands，2007.

[15]李明明.Fisher與小樣本及“n維幾何法”[D].天津：天津財經大學，2014.

[16]LINTC.Development of U.S.air force international ballistic missle weapon systems[J].Journal of Spacecraft and Rockets，2003，40（4）：491-509.

（編輯：商丹丹）

The method of compatibility check of testability growth test data based on Fisher-statistics

WANG Jing1，HE Huafeng1，LI Tianmei1，XU Congqi2，YANG Zonghao1，HAN Congcong1
（1.Department of Control Engineering，Rocket Force University of Engineering，Xi’an 710025，China；2.The Institute of Construction Engineering Research，General Logistics Department of PLA，Xi’an 710032，China）

The method of compatibility check based on Fisher-statistics is put forward to verify the consistency of testability growth test data and field data during the process of testability evaluation.Aiming at the data of small sample and success or failure，a sequential constraint model is proposed to test the growth trend of test data，constructing Fisher-statistics based on hypergeometric distribution and judging the relationship between two adjacent stages，then the conclusions about the overall consistency between the growth test data and the field data are obtained.Validation of the method is presented via application examples.Results indicate that the method can also make a reasonable decision about the overall consistency in small sample sizes whose number is less than 26.In practical engineering，it’s a better choice to set growth stage after synthesizing the influence of cost，stability and technical level at a given level of significance.

testability evaluation；compatibility check；growth test；Fisher-statistics

A

1674-5124（2017）08-0011-03

2016-09-22；

2016-11-18

國家自然科學基金項目（61304103）

王京（1992-），男，河南鄭州市人，碩士研究生，專業方向為測試性驗證與評估。

10.11857/j.issn.1674-5124.2017.08.003