動量觀點與其他相關知識綜合問題分析
李紅偉
(江西省全南中學 江西 贛州 341800)
動量觀點與其他相關知識綜合問題分析
李紅偉
(江西省全南中學 江西 贛州 341800)
2017年高考考試大綱已公布,新大綱進一步細化對“理解能力、推理能力、分析綜合能力、應用數學處理物理問題的能力、實驗能力”的考查要求,增加例題進行闡釋,明確能力考查的具體要求;同時刪去人教版《物理·選修2-2》的內容,將《物理·選修3-5》的內容列為必考,《物理·選修3-3》、《物理·選修3-4》作為選考模塊的內容和范圍都不變,考生從中任選1個模塊作答.《物理·選修3-5》的內容列為必考,動量和能量守恒、力與運動、電磁感應綜合將成為高考考查的熱點、亮點.下面對動量觀點與其他相關知識綜合的問題進行分析.
1 利用動量定理求變力的沖量
在日常生活和生產中,常常會碰到變力作用在物體上的問題,在高中階段不能直接求得變力的沖量.但如果力是線性變化時,我們可以將變力轉化為平均力再求變力的沖量;或已知物體質量和初、末速度,也可以利用動量定理求解變力的沖量.
【例1】如圖1所示,A和B兩小物快用輕彈簧相連,懸于輕繩下,A和B的質量分別為m1,m2.開始時,A和B均靜止.剪斷細線,經一段時間后,A和B的速度大小分別為v1和v2,方向均向下,求這段時間內彈簧的彈力對A和B的沖量.
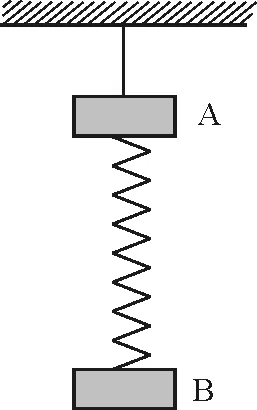
圖1 例1題圖
解析:設彈簧對A的沖量IA=I,則彈簧對B的沖量必為IB=-I,分別以A和B為研究對象,且以豎直向下方向為正方向,則
m1gt+I=m1v1
m2gt-I=m2v2
消去t,可解出
點評:如果以A和B系統為研究對象列方程,則
(m1+m2)gt=m1v1+m2v2
動量定理不僅適用于恒力作用,也適用于變力作用過程,利用動量定理只考慮初末狀態,不涉及運動過程,這是利用動量定理解決實際問題的優越性所在.
2 動量定理在流體問題的應用
在處理有關流體(如水、空氣、高壓燃氣等)撞擊物體表面產生沖力(或壓強)的問題,高中階段只能利用動量定理來進行解決.
【例2】某種氣體分子束由質量m=5.4×10-26kg,速度v=460 m/s的分子組成,各分子都向同一方向運動,垂直地打在某平面上后又以原速率反向彈回,如分子束中每立方米的體積內有n0=1.5×1020個分子,求被分子束撞擊的平面所受到的壓強.
解析:設在Δt時間內射到面積為S的某平面上的氣體的質量為ΔM,則
ΔM=vΔtSn0m
取ΔM為研究對象,平面作用到氣體上的反作用力為F,以分子碰撞平面彈回速度方向規定為正方向,由動量定理得
FΔt=ΔMv-(-ΔMv)
解得
F=2v2Sn0m
根據牛頓第三定律,平面受到的壓強p為
點評:處理流體問題問題的關鍵是選在極短時間Δt內射到物體表面上的流體為研究對象.這類問題往往與受力平衡、牛頓第三定律、壓強等知識點聯系在一起進行考查.
3 動量定理與電磁感應問題的綜合
導體棒切割磁感線產生感應電流,從而使導體棒又受到安培力作用.導體棒運動的形式有勻速、勻變速和非勻變速3種.對勻速、勻變速兩種情況可以用牛頓定律進行求解,對非勻變速這種情況,由于安培力發生變化,且又涉及到位移、速度、電荷量等問題時,如果用能量守恒和動量守恒定律求解,往往會無法求解,但利用動量定理求解往往能收到意想不到的效果.
【例3】如圖2所示,水平光滑導軌與電阻R連結,處在磁感應強度為B的豎直向上的勻強磁場中,一質量為m,長為L的導體棒以初速度v0向右運動,導體棒電阻和導軌電阻不計,設磁場范圍足夠大,導軌足夠長,在導體棒運動的整個過程中,求:
(1)通過電阻R的電荷量是多少?
(2)導體棒運動的距離有多遠?
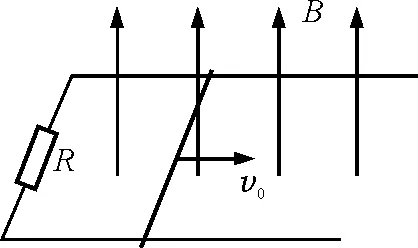
圖2 例3題圖
解析:(1)設導體棒運動時間為t,平均電流為I,通過電阻R的電荷量為q,則
q=It
根據動量定理得
BILt=mv0
由以上兩式解得
(2)由電路知識和法拉第電磁感應定律得
由以上兩式解得
結合第(1)問結論得
點評:通過例題的分析,當導體切割磁感線而產生感應電流,如果感應電流不恒定,導體所受到的安培力也不恒定而做變速運動時,若涉及位移、速度、電荷量等問題時,可以利用動量定理來處理,使得看似疑難的問題迎刃而解.
4 動量守恒在電磁感應問題中的運用
在相互平行的水平軌道間的雙棒做切割磁感線運動時,由于這兩根導體棒所受的安培力等大反向,合外力為零,若不受其他外力,則兩導體棒的總動量守恒,故解決此類問題往往應用動量守恒定律來處理.
【例4】兩根足夠長的固定的平行金屬導軌位于同一水平面內,兩導軌間的距離為L.導軌上面橫放著兩根導體棒ab和cd,構成矩形回路,如圖3所示.兩根導體棒的質量皆為m,電阻皆為R,回路中其余部分的電阻可不計.在整個導軌平面內都有豎直向上的勻強磁場,磁感應強度為B.設兩導體棒均可沿導軌無摩擦地滑行.開始時,棒cd靜止,棒ab有指向棒cd的初速度v0.若兩導體棒在運動中始終不接觸,求:
(1)在運動中產生的焦耳熱最多是多少?

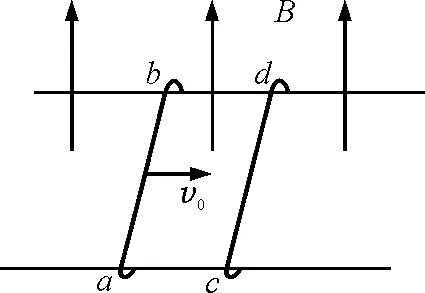
圖3 例4題圖
解析:(1)從初始至兩棒達到速度相同的過程中,兩棒總動量守恒,則
mv0=2mv
根據能量守恒,整個過程中產生的總熱量

此時回路中的感應電動勢和感應電流分別為
此時cd棒所受的安培力
F=IBl
cd棒的加速度
由以上各式,可得
點評:在這類問題中,當兩棒速度達到相同后,回路面積保持不變,磁通量不變化,不產生感應電流,兩棒以相同的速度v做勻速運動,兩金屬棒作用就可看成完全非彈性碰撞模型.
5 動量守恒在原子核衰變問題中的運用
原子核衰變時內力遠大于外力,衰變過程遵循動量守恒定律;衰變后的粒子在電場、磁場中或正交電場磁場中所做的運動情況由初速度和所受合力共同決定.
【例5】在勻強磁場中的A點有一個靜止的原子核發生衰變,衰變后形成如圖4所示的兩內切圓軌跡,則
(1)該核發生的是什么衰變?
(2)如果已知大圓和小圓軌跡半徑之比為44:1,則該放射性元素的原子序數是多少?
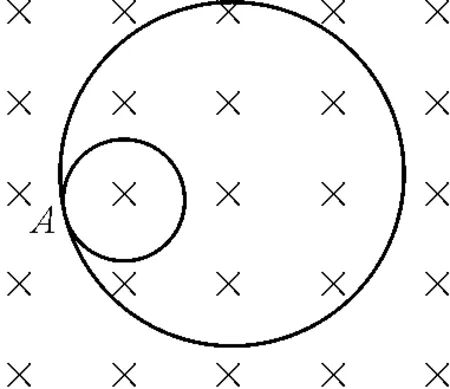
圖4 例5題圖
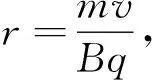
點評:本試題主要考查對向心力、牛頓第二定律、帶電粒子在勻強磁場中的運動等考點的理解.在勻強磁場中靜止的原子核發生衰變,β衰變后形成兩內切圓軌跡,a衰變后形成兩外切圓軌跡.
6 多體碰撞問題
對于動量守恒定律的應用問題,2014年考試大綱將“只限于一維兩個物體的碰撞問題”調整為“只限于一維”,從而多體碰撞問題成為考查熱點.近3年高考試題中都有所體現.
【例6】如圖5所示,3個直徑相同的小球靜止在足夠長的光滑水平面上,A和C 2球的質量均為m,B球的質量為km(k>1).給A球一個水平向右的初速度v0,B球先與A球發生彈性正碰,再與C球發生彈性正碰.求系數k的值為多大時,B與C碰后瞬間B球的速度最大?
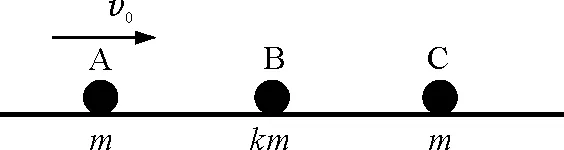
圖5 例6題圖
解析:設A和B發生彈性碰撞后的速度分別為vA和vB1,由動量守恒定律及機械能守恒定律,則
mv0=mvA+kmvB1
解得
設B和C發生彈性碰撞后的速度分別為vB2和vC,同理有
代入并整理得
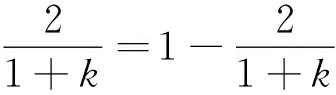
點評:此類問題中,損失的機械能往往用碰撞前后系統損失的動能來描述,損失的動能轉化為其他形式的能量,如系統增加的內能最大,對彈簧系統彈簧的彈性勢能最大等.
2016-12-13)
教與帶兼程,苦與樂同在.

