萬有引力定律的應用問題歸類例析①
(廣東省五華縣田家炳中學,廣東 梅州 514400)
萬有引力定律的應用問題歸類例析①
古煥標
(廣東省五華縣田家炳中學,廣東 梅州 514400)
運用萬有引力定律求解天體(衛星)運動問題一直是高考命題熱點,此類習題題型較多,本文對該類問題進行了分類,并總結了解題的中心方法是“萬有引力提供向心力”和“黃金代換”。
萬有引力;向心力;黃金代換
萬有引力定律部分內容比較抽象,習題類型較多,在教學中學生普遍反映這一部分內容變化繁雜,學習思路不清晰,難懂、難學。筆者根據自己的教學經驗,將這一部分知識的解題思路進行歸納,經過實際教學實踐,絕大部分學生反映采用這種方法學習以后,學習思路清晰了,知識掌握牢固了,學習負擔減輕了,以下針對萬有引力的不同類型習題的解法加以歸類、分析。
1 解題思路
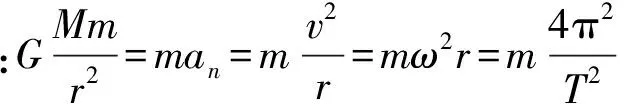
2 問題歸類
2.1 星體表面上的重力加速度
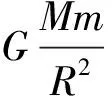
除此以外,還可通過在星體表面涉及的自由落體、豎直上拋、平拋等拋體運動形式來求星體表面的重力加速度g。
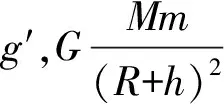
例1:一宇宙飛船繞地心做半徑為r的勻速圓周運動,飛船艙內有一質量為m的人站在可稱體重的臺秤上。用R表示地球的半徑,g表示地球表面處的重力加速度,g′表示宇宙飛船所在處的地球引力加速度,FN表示人對秤的壓力,下列說法中正確的是( )。
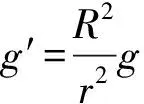
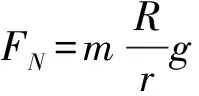
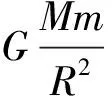
2.2 中心天體的質量M和密度ρ
當衛星繞行星或行星繞恒星做勻速圓周運動時,根據題目提供的不同條件,在下面4種情況下都可求解中心天體的質量。
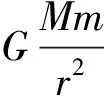

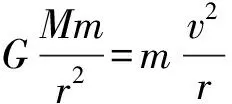
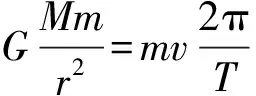
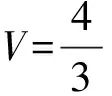
例2:要計算地球的質量,除已知的一些常數外還需知道某些數據,現給出下列各組數據,可以計算出地球質量的是( )。
A.已知地球半徑R
B.已知衛星繞地球做勻速圓周運動的軌道半徑r和線速度v
C.已知衛星繞地球做勻速圓周運動的線速度v和周期T
D.已知地球公轉的周期T′及運轉半徑r′
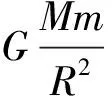
2.3 衛星運行的參量
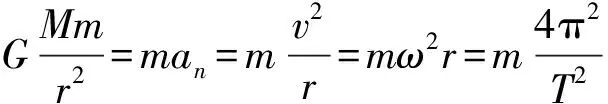
例3:設地球質量為月球質量的81倍,地球半徑是月球半徑的4倍,若探測器甲繞地球和探測器乙繞月球做勻速圓周運動的半徑相同,則( )。
A.甲與乙線速度之比為9∶2
B.甲與乙線速度之比為1∶9
C.甲與乙向心加速度之比為81∶1
D.甲與乙運動周期之比為1∶1
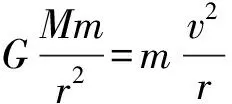
2.4 赤道上的物體、近地衛星、同步衛星運行參量的比較
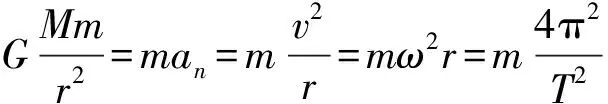
例4:有a、b、c、d四顆衛星,a還未發射,在地球赤道上隨地球一起轉動,b在地面附近近地軌道上正常運動,c是地球同步衛星,d是高空探測衛星,設地球自轉周期為24h,所有衛星的運動均視為勻速圓周運動,各衛星排列位置如圖1所示,則下列關于衛星的說法中正確的是( )。
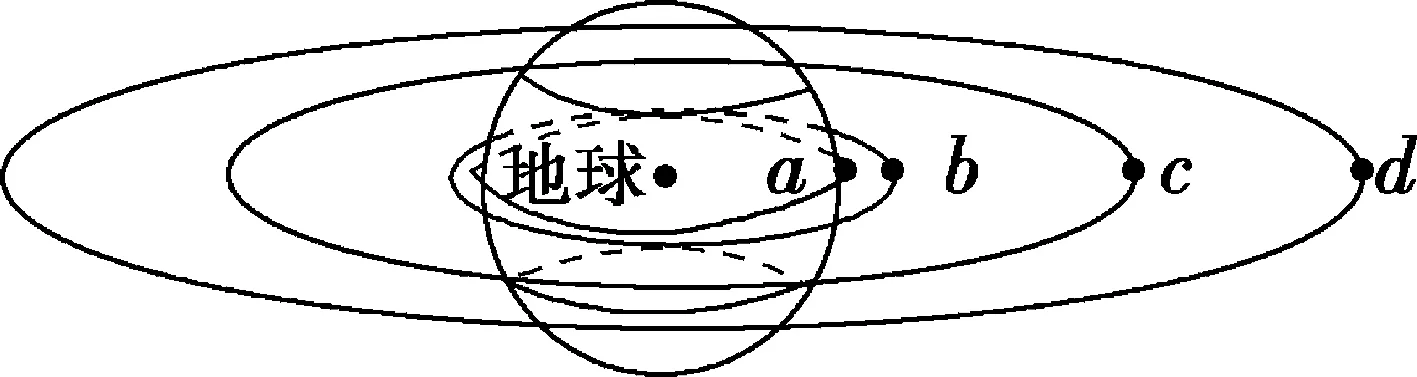
圖1
A.a的向心加速度等于重力加速度g
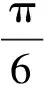
C.b在相同的時間內轉過的弧長最長
D.d的運動周期可能是23h
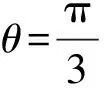
2.5 衛星的變軌問題
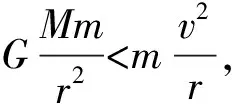
例5:如圖2所示是“嫦娥三號”飛行軌道示意圖。假設“嫦娥三號”運行經過P點第一次通過近月制動使“嫦娥三號”在距離月面高度為100km的圓軌道Ⅰ上運動,再次經過P點時第二次通過近月制動使“嫦娥三號”在距離月面近地點為Q、高度為15km,遠地點為P、高度為100km的橢圓軌道Ⅱ上運動,下列說法正確的是( )。

圖2
A.“嫦娥三號”在距離月面高度為100km的圓軌道Ⅰ上運動時速度大小可能變化
B.“嫦娥三號”在距離月面高度100km的圓軌道Ⅰ上運動的周期一定大于在橢圓軌道Ⅱ上運動的周期
C.“嫦娥三號”在橢圓軌道Ⅱ上運動經過Q點時的加速率一定大于經過P點時的加速度
D.“嫦娥三號”在橢圓軌道Ⅱ上運動經過Q點時的速率可能小于經過P點時的速率
解析:“嫦娥三號”在距離月面高度為100km的圓軌道上運動是勻速圓周運動,速度大小不變,選項A錯誤;由于圓軌道的軌道半徑大于橢圓軌道半長軸,根據開普勒定律,“嫦娥三號”在距離月面高度100km的圓軌道Ⅰ上運動的周期一定大于在橢圓軌道Ⅱ上運動的周期,選項B正確;由于在Q點“嫦娥三號”所受萬有引力大,所以“嫦娥三號”在橢圓軌道Ⅱ上運動經過Q點時的加速度一定大于經過P點時的加速度,選項C正確;“嫦娥三號”在橢圓軌道上運動的引力勢能和動能之和保持不變,Q點的引力勢能小于P點的引力勢能,所以“嫦娥三號”在橢圓軌道Ⅱ上運動到Q點的動能較大,速度較大,所以“嫦娥三號”在橢圓軌道Ⅱ上運動經過Q點時的速率一定大于經過P點時的速率,選項D錯誤。
2.6 中心天體的第一宇宙速度
地球的第一宇宙速度是衛星運行半徑為地球半徑時的環繞速度,與此類似,其他星球的第一宇宙速度是衛星的運行半徑為此星球半徑時的環繞速度,計算第一宇宙速度一般有下面兩種方法。
例6:某星球的半徑為R,在其表面上方高度為aR的位置,以初速度v0水平拋出一個金屬小球,水平射程為bR,a、b均為數值極小的常數,則這個星球的第一宇宙速度為( )。
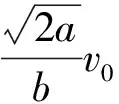
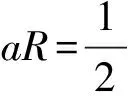
2.7 雙星類問題
(1)雙星問題的特點:① 兩星的運動軌道為同心圓,圓心是它們之間連線上的某一點。
② 兩星的向心力大小相等,由它們間的萬有引力提供。
③ 兩星的運動周期、角速度相同。
④ 兩星的軌道半徑之和等于兩星之間的距離,即r1+r2=L。
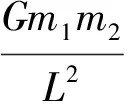

圖3
例7:如圖3所示,由兩顆星球組成的雙星,在相互之間的萬有引力作用下,繞連線上的O點做周期相同的勻速圓周運動。現測得兩顆星之間的距離為L,質量之比為m1∶m2=3∶2,下列說法中正確的是( )。
A.m1、m2做圓周運動的線速度之比為3∶2
B.m1、m2做圓周運動的角速度之比為3∶2
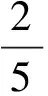
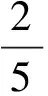
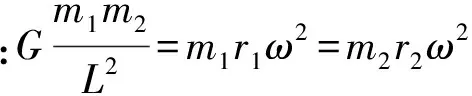
2.8 天體運動中的能量變化
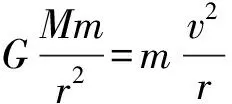
例8:目前,在地球周圍有許多人造地球衛星繞著它運轉,其中一些衛星的軌道可近似為圓,且軌道半徑逐漸變小。若衛星在軌道半徑逐漸變小的過程中,只受到地球引力和稀薄氣體阻力的作用,則下列判斷正確的是( )。
A.衛星的動能逐漸減小
B.由于地球引力做正功,引力勢能一定減小
C.由于氣體阻力做負功,地球引力做正功,機械能保持不變
D.衛星克服氣體阻力做的功小于引力勢能的減小
3 結語
應用萬有引力定律解決問題的習題題型較多,涉及的題型以天體運動為核心,如運行速度、估算天體質量或平均密度、變軌問題等,解題的方法是“萬有引力提供向心力”和運用“黃金代換式”:GM=gR2。
[1] 馮占余.萬有引力及天體問題考點分析[J].數理化學習,2011,(5):71-73.
[2] 章克文.2015高考萬有引力與航天類試題評析[J].物理教學探討,2015,33(9):45-47.
①本文系梅州市普教系統“百千萬人才工程”第五期立項課題“高中物理習題的創新與解題策略的研究”(課題編號:20160630052)的成果之一。

