基于DTW算法的云南昭通地區場次洪水相似性研究

(1.云南省水文水資源局 昭通分局，云南 昭通 657000; 2.長江科學院 農業水利研究所，湖北 武漢 430010; 3.西藏自治區水土保持局，西藏 拉薩 850000)

基于DTW算法的云南昭通地區場次洪水相似性研究

任繼周1彭德才1喬偉2萍央3

(1.云南省水文水資源局昭通分局，云南昭通657000; 2.長江科學院農業水利研究所，湖北武漢430010; 3.西藏自治區水土保持局，西藏拉薩850000)

利用隨機水文學思想分析場次洪水的歷史相似性對洪水預報、防洪調度等具有重要的現實意義。采用動態時間扭曲算法，對云南省昭通市綏江縣大汶溪流域1961～2014年洪峰流量進行了頻率分析，并對新華水文站場次洪水過程進行了相似性分析。分析得出，動態時間扭曲算法作為數據挖掘領域一種相似性分析的方法，能夠對原始數據進行充分挖掘，從而有效尋找出不同場次洪水中相似性最高的組合。研究成果可為場次洪水特征分析、洪水預報等提供參考。

場次洪水；相似性；動態時間扭曲；云南昭通

1 研究背景

洪水是我國江河的主要自然災害，直接威脅著區域社會經濟的發展和人民生命財產安全。目前，我國學者對洪水的分析主要集中在三方面：①洪水的頻率或重現期分析，如洪峰流量的頻率曲線擬合及洪峰、洪量、洪水歷時等多要素聯合概率分析等；②場次洪水過程的特征分析，如洪水過程形態、漲洪歷時等；③洪水過程與暴雨過程的關系，包括產流系數、徑流組成、洪水峰現時間滯后最大雨峰的時間等。從水文時間序列分析的角度來看，以往對場次洪水歷史相似性的研究較少。根據隨機水文學的思想，未來的洪水過程是歷史上某種洪水過程的重現，充分利用洪水信息，可對未來可能發生的洪水形勢進行預估，從而掌握洪水全貌[1]。因此，通過隨機水文學思想分析場次洪水的歷史相似性對洪水預報、防洪調度等具有重要的現實意義。

時間序列相似性研究中的動態時間扭曲算法(Dynamic Time Warping，簡稱DTW)最早起源于語音識別領域，隨后被廣泛應用于各種領域進行數據挖掘，整個計算過程等同于動態尋優[2]。該方法已被應用于水文時間序列的相似性分析，并取得了較好的效果。因此，本文將該方法應用于云南省昭通市綏江縣大汶溪流域，在對流域內新華水文站1961～2014年洪峰流量進行頻率分析的基礎上，采用DTW方法對實測54場典型洪水過程進行場次洪水相似性分析，探尋歷史洪水的相似性，以期為場次洪水特征分析、洪水預報等提供參考。

2 資料與方法

2.1 數據資料

綏江縣位于昭通市北部，東與水富縣相鄰，南與鹽津縣、永善縣接壤，西、北面與四川省的屏山縣、雷波縣隔江相望；地理坐標介于東經103°47′～104°16′、北緯28°21′～28°40′之間。縣境東西長約48.5 km、南北寬36 km，總面積 746.3 km2。綏江縣屬亞熱帶濕潤季風氣候，冬無嚴寒，夏無酷暑。特殊的氣候條件、地形地貌和人類活動的影響使綏江縣成為山洪地質災害的重災區。大汶溪流域屬于金沙江右岸的一級支流，發源于綏江縣板栗鄉大堡頂，流經板栗鄉后稱板栗河，主要支流有銅廠河、黃龍溪，全流域面積391 km2。新華水文站于1961年設立，位于流域下游，屬于出口控制站，控制流域面積324 km2，河長35.7 km，河道坡度29.0‰，流域平均高程1 214 m。

2.2 研究方法

DTW算法具體過程如下[3]：假定兩個時間序列為A=和B=，構建一個k×s階的矩陣，該矩陣中存放的元素即為兩個時間序列對應點間的距離，即矩陣中的第(i，j)個元素為點ai和點bj之間的距離d(xi，yj)，距離的計算通常采用d(xi,yi)=(xi-yi)2。上述k×s階矩陣中，元素的連續集構成了扭曲路徑W，其中W的第m個元素被定義為wm=(i，j)m，因此可以得到一個路徑集：

W={w1,w2,…,wm,…,wM|max(k,s)

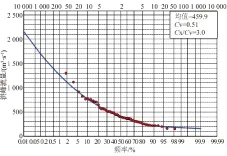
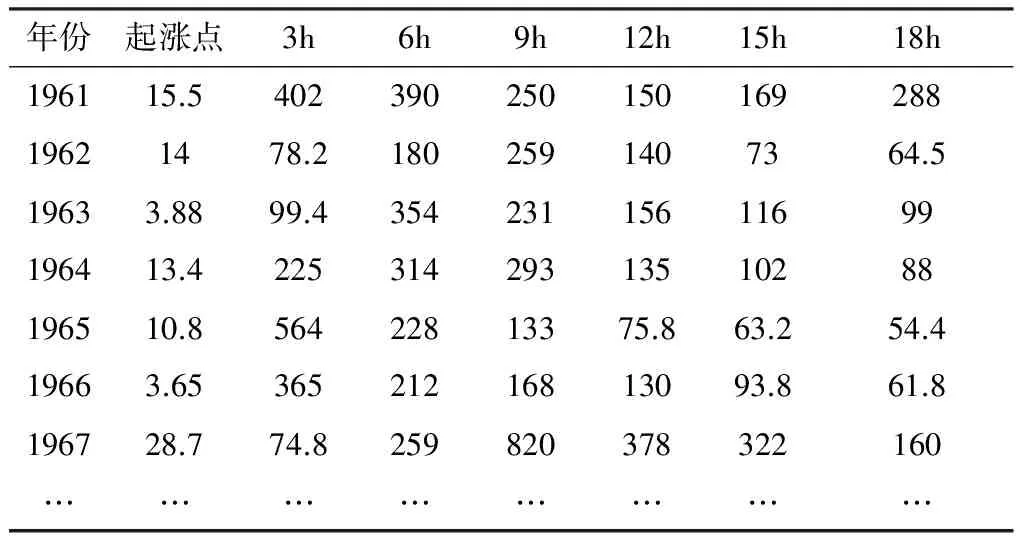
M

(1)

扭曲路徑要求滿足連續性、邊界條件以及單調性條件限制。

(1)邊界條件：w1=(1，1)，wM= (k，s)。

(2)連續性：給定wm= (a，b)，wm-1=(a′，b′)，要求a-a′≤1和b-b′≤1，該連續性要求扭曲路徑必須是連續的，不能有跳過某點的情況。

(3)單調性：給定wm= (a，b)，wm-1=(a′，b′)，要求a-a′≥0和b-b′≥0。也就是說，在動態尋優的過程中，不能再向相反的方向尋優。

從以上要求可知，對于兩個時間序列，有很多路徑都滿足以上條件，但最優的路徑只有一條。為了尋找最佳路徑，需要定義從起點到終點的累積距離，并根據累積距離求得扭曲代價，累積距離最小則為最優，最優路徑滿足最小扭曲代價，如下式：

(2)

構造累積距離矩陣r公式如下

(3)

初始條件設置為r(1,1)=d(p1,q1)。從兩個序列起始點(1，1)開始，根據公式(2)與公式(3)迭代計算累積距離，并最終得到最小累加值r(k,s)，該累加值即為時間序列P和Q的dDTW距離。

3 結果與討論

3.1 洪峰流量頻率分析

首先對新華水文站1961～2014年實測洪峰流量進行頻率分析。頻率分析采用國內常用的P-Ⅲ型曲線進行。經過適線，頻率分析結果如圖1所示。其中，新華水文站洪峰流量均值約為460 m3/s，變差系數Cv值為 0.51，Cs/Cv=3.0。從圖1可以看出，P-Ⅲ型曲線的擬合效果較好，且該水文站洪峰流量的頻率幾乎均大于5%，即新華水文站洪峰流量重現期基本小于20 a一遇。100 a一遇的洪峰流量為1 251.86 m3/s，50 a一遇的洪峰流量為1 111.2 m3/s，20 a一遇的洪峰流量為921.7 m3/s，10 a一遇的洪峰流量為744.4 m3/s。該站點洪峰流量均值460 m3/s對應的重現期約為2.5 a。

圖1 新華水文站洪峰流量P-Ⅲ型曲線

3.2 場次洪水相似性分析

在對場次洪水進行相似性分析的過程中，重點考慮場次洪水的形狀特征，即從洪水起漲到出現洪峰再到洪水退去的整個過程中。洪水流量的變化過程對研究當地洪水變化形態、制定山洪預警方案有重要意義。在1961～2014這54 a中，每年的場次洪水不僅僅只有一場，有時連續兩場降雨間隔較短，導致由降雨引起的兩場洪水出現疊加的情況，不利于單次洪水過程的分析。因此，本文在場次洪水相似性分析的過程中，每年僅選取一場洪水進行研究。選取的原則為：每年選取一場由單次降雨引起的單場次洪水，若符合該類型的洪水超過一場，則在其中選取洪峰流量最大的那一場洪水作為研究對象。為描述洪水的變化過程，從洪水起漲算起，取洪水起漲后3，6，9，12，15 h及18 h對應的洪峰流量共7個數字描述場次洪水過程，如表1中所列即為1961～1967年場次洪水待分析數據。

表1 代表年場次洪水流量過程 m3/s

準備好待分析場次洪水數據后，便可采用DTW算法對歷年場次洪水過程進行相似性分析。DTW算法的目的是得到不同年份場次洪水過程數據間的dDTW距離，并用一個方陣來存放所有子序列之間的dDTW距離，記為D_matrix：

D_matrix=

(4)

式中，f1，f2，…，fn為n個子序列，即子序列樣本數為n。矩陣的第(k，s)元素代表第k個子序列和第s個子序列之間的dDTW距離，即dDTW(fk，fs)。根據矩陣的定義可知，D_matrix是一個對稱矩陣，因為序列自身與自身完全相似，故矩陣對角線為0。根據DTW算法原理可知，在距離方陣中，數值越小則兩組數據越相似。計算得到的D_matrix矩陣如下所示。

(5)

從D_matrix的矩陣計算結果可以看出，不同年份之間的場次洪水相似性存在較大的差異。其中，計算得到最小的dDTW距離為75.8，對應年份為1976年與1993年，說明這兩場洪水的相似度最高；計算得到最大的dDTW距離為2 184，對應年份為1974年與2011年，說明這兩場洪水的相似度最低。

根據矩陣的計算結果，分別在矩陣中選擇4組dDTW距離最小的年份繪圖對比，所選擇的年份及其dDTW距離列表2如下，場次洪水過程對比如圖2所示。

表2 相似度最高的4組場次洪水對比

從圖2可以看出，1976年與1993年的場次洪水過程相似性最高，這兩場洪水過程線從起漲到洪峰，再到退水的整個過程非常相似，幾乎完全重合。其他3組場次洪水的過程線相似度也較高，不論是洪水過程線的形態還是洪峰流量，差別并不大。這說明動態時間扭曲算法能夠在眾多場次洪水數據中尋找出相似性最高的組合，其相似性搜索的效果顯著。同時，從圖2中的4幅圖中可以看出，新華水文站實測得到的場次洪水形態大致相似，屬于尖瘦峰型，即在洪水過程中，漲洪歷時較短且漲勢兇猛，退水過程相較漲水過程緩慢。此種類型洪水由于漲水快、洪量大，易造成山洪災害，是山洪災害中最需要預警的一種洪水類型。

圖2 相似性最高的4組場次洪水對比

根據D_matix計算結果，將矩陣各行(或各列)相加，即可得到每個年份場次洪水與其他年份場次洪水相似度的計量總和，如表3所示。從表3可以看出，ΣdDTW最小的年份是1966年，與其他年份dDTW距離之和為19 868.05；ΣdDTW最大的年份是1974年，該年份與其他年份dDTW距離之和為67 344.58。這說明，1966年的場次洪水過程與其他年份的相似度最高，而1974年的場次洪水過程與其他年份相似度最低。

表3 各年份dDTW距離之和

4 結 論

本文利用動態時間扭曲算法，在對云南省昭通市綏江縣大溪溝流域1961～2014年洪峰流量進行頻率分析的基礎上，對新華水文站場次洪水過程進行了相似性分析，主要結論如下：

(1)新華水文站洪峰流量均值約為460 m3/s，變差系數Cv值為 0.51，Cs/Cv=3.0。該水文站100 a一遇的洪峰流量為1 251.86 m3/s，50 a一遇的洪峰流量為1 111.2 m3/s，20 a一遇的洪峰流量為 921.7 m3/s，10 a一遇的洪峰流量為 744.4 m3/s。均值洪峰流量對應的重現期約為 2.5 a。

(2)經過動態時間扭曲算法的相似性搜索，1976年與1993年的場次洪水相似性最高，其dDTW距離為 75.8；1974年與2011年的場次洪水相似度最低，其dDTW距離為2 184。ΣdDTW最小的年份是1966年，說明1966年的場次洪水過程與其他年份的相似度最高；ΣdDTW最大的年份是1974年，說明1974年的場次洪水過程與其他年份相似度最低。

總之，動態時間扭曲算法作為數據挖掘領域一種相似性分析的方法，能夠對原始數據進行充分挖掘，從而有效尋找出不同場次洪水中相似性最高的組合。該方法可在水文領域繼續推廣，如應用到暴雨過程與洪水過程及洪峰與洪量過程的相似性分析中。

[1] 牛俊. 流域場次暴雨洪水相似性分析的可拓模型構建及應用[D]. 南京：河海大學, 2006.

[2] 劉衛林, 董增川, 梁忠民,等. 暴雨洪水相似性分析及其應用研究[J]. 中國農村水利水電, 2007(2):132-135.

[3] 楊艷林, 葉楓, 呂鑫,等. 一種基于DTW聚類的水文時間序列相似性挖掘方法[J]. 計算機科學, 2016, 43(2):245-249.

(編輯：朱曉紅)

2017-05-09

國家自然科學基金(51509010)；中央級公益性科研院所基本科研業務費資助項目(CKSF2016039/NS、CKSF2016028/NS)

任繼周，男，云南省水文水資源局昭通分局，高級工程師.

喬偉，女，長江科學院農業水利研究所，工程師.

1006-0081(2017)08-0035-04

TV122

：A