二項分布參數(shù)的無先驗信息Bayes估計與點(diǎn)估計的思考

侯瑞環(huán) 徐翔燕

二項分布參數(shù)的無先驗信息Bayes估計與點(diǎn)估計的思考

侯瑞環(huán) 徐翔燕

結(jié)合《數(shù)理統(tǒng)計》教學(xué)過程中的對點(diǎn)估計和Bayes估計的講解，從實(shí)際應(yīng)用的角度出發(fā)思考二項總體參數(shù)的無先驗信息Bayes估計與點(diǎn)估計之間的關(guān)系：當(dāng)樣本容量n≥971時，兩種估計的誤差達(dá)到0.001甚至更小；并且，隨著樣本量不斷增加兩種估計結(jié)果趨于一個穩(wěn)定的真實(shí)值。

點(diǎn)估計作為大學(xué)《數(shù)理統(tǒng)計》的教學(xué)中最簡單、最有效的參數(shù)估計方法顯得非常重要，也是統(tǒng)計推斷中不可或缺的內(nèi)容。通常，點(diǎn)估計的方法主要有矩估計和極大似然估計。然而，無論是矩估計還是極大似然估計都有著非常明顯的優(yōu)點(diǎn)和缺陷。矩估計應(yīng)用樣本信息對總體分布部分特征做統(tǒng)計推斷以達(dá)到對整個總體特征的推斷，這顯然很難完成；極大似然估計較多的注重總體信息的應(yīng)用，與矩估計相比有顯著的改善。但是，這些經(jīng)典參數(shù)估計方法都缺少了對參數(shù)本身的思考，只是從樣本本身出發(fā)，將未知參數(shù)默認(rèn)為未知常數(shù)來完成統(tǒng)計推斷，導(dǎo)致了參數(shù)本身信息的流失，這是一種明顯的信息浪費(fèi)。區(qū)別于經(jīng)典統(tǒng)計學(xué)派的Bayes學(xué)派提出了參數(shù)的Bayes估計很大程度上解決了這一問題，有效的利用了參數(shù)本身的信息和樣本信息，使得估計效果在一般情況下都優(yōu)于點(diǎn)估計方法。Bayes估計方法主要依賴于參數(shù)的后驗分布，一般情況下，參數(shù)的后驗分布借助條件概率得到，這種求解后驗分布的方法存在爭議。目前，在沒有更好解決后驗分布的情況下可以認(rèn)為這種辦法比較有效，但是參數(shù)的后驗分布在很多情況下較難得到。正因為如此，本文做出這樣的思考：在對二項分布參數(shù)的先驗信息一無所知時，對參數(shù)的估計有沒有必要堅持用Bayes估計？能否得到一個樣本容量使得Bayes估計和點(diǎn)估計幾乎一致？

點(diǎn)估計與Bayes估計

參數(shù)的點(diǎn)估計。設(shè)X1,L,Xn是來自于二項分布總體b(n,p)的樣本，計算總體參數(shù)p矩估計和極大似然估計，以定理2.1形式給出。

定理2.1 在上述假設(shè)的基礎(chǔ)上p的矩估計和極大似然估計分別為:

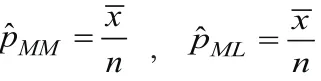
定理2.1簡要證明：

由樣本總體分布可知，二項分布(,)bnp的總體矩為()EXnp=，所以根據(jù)矩法估計的思想用樣本矩代替總體矩可得到

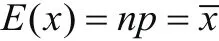
由此可以計算參數(shù)p的矩估計。

總體分布的密度函數(shù)為：

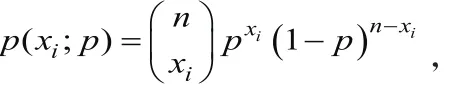
因此可以得到對數(shù)似然函數(shù)為：

對（1）式關(guān)于參數(shù)p求導(dǎo)可以得到其極大似然估計。

根據(jù)上述定理可以得到這樣一個推論：在n次試驗中某一事件發(fā)生xi次，參數(shù)所對應(yīng)極大似然估計為。

參數(shù)的Bayes估計。在此假設(shè)對參數(shù)先驗信息一無所知，根據(jù)Bayes本人的建議按“同等無知”的原則處理，即可以設(shè)定參數(shù)p的先驗分布π(p)=U (0,1)。在這種假設(shè)下可以得到參數(shù)的Bayes估計如定理2.2。

定理2.2設(shè)在上述先驗分布的假設(shè)下，二項分布b(n,p)的參數(shù)p的Bayes估計為：

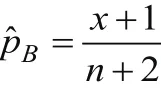
其中x=xi，i=1,2,L,n。

定理2.2簡要證明：由上述假設(shè)可知，π(p)=U(0,1)，同時可以寫出隨機(jī)變量X與參數(shù)p的聯(lián)合分布

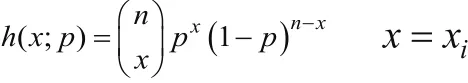
可以得到X的邊緣密度

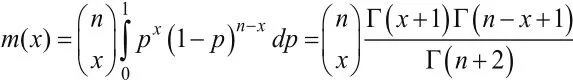
即可得到參數(shù)p的后驗分布

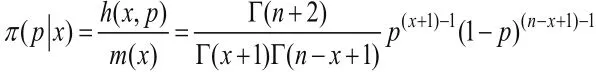
上式表明參數(shù)p的后驗分布為貝塔分布Be(x+1,n-x+1)，因此可以得到參數(shù)的估計為：

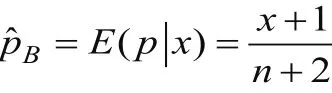
結(jié)果得證。

數(shù)據(jù)模擬與誤差分析。對二項分布參數(shù)基于點(diǎn)估計結(jié)果和Bayes估計樣本容量分別為15、30、100和200的數(shù)據(jù)模擬結(jié)果見圖1～4，并進(jìn)行誤差的比較與分析。

對二項分布參數(shù)估計而言，當(dāng)樣本容量較小時，可以看出極大似然估計結(jié)果與Bayes估計結(jié)果相差較大（圖1、2），然而在中位數(shù)處取值相等；同時可以看出Bayes估計在極端情況下，估計結(jié)果更符合人們的正常理念。當(dāng)樣本容量不斷增大時，極大似然估計與Bayes估計在結(jié)果上差異越來越小（圖3、4），當(dāng)971≥n時，這兩個估計結(jié)果只差達(dá)到0.001甚至更小，此時就二項分布參數(shù)估計的應(yīng)用而言，可以考慮用點(diǎn)估計得到參數(shù)的結(jié)果代替Bayes估計的結(jié)果。

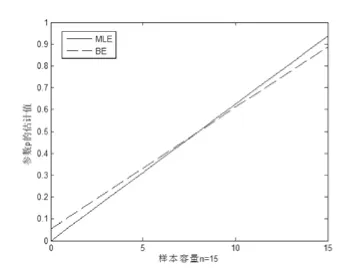
圖1 樣本容量為15的估計擬合

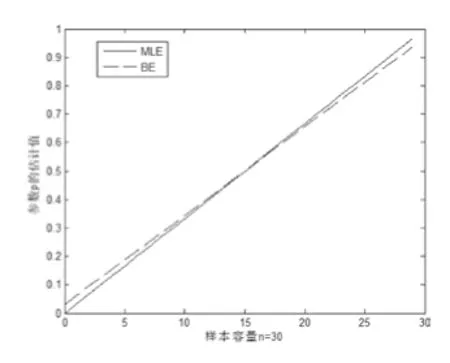
圖2 樣本容量為30的估計擬合

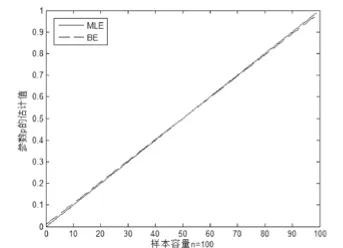
圖3 樣本容量為100的估計擬合

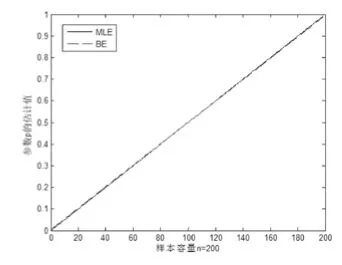
圖4 樣本容量為200的估計擬合

為了更好地說明這一觀點(diǎn)，在此通過取不同的樣本容量n對同一個二項分布的參數(shù)分別用點(diǎn)估計和Bayes 估計方法做數(shù)據(jù)模擬。得到在不同估計方法下估計值與參數(shù)真實(shí)值之間的誤差，結(jié)果見表1。

由表1結(jié)果可知，點(diǎn)估計與Bayes估計結(jié)果都隨著樣本容量的增加而減小，其中點(diǎn)估計得到結(jié)果與真實(shí)值之間是一個固定的單點(diǎn)誤差值，而Bayes估計與真實(shí)值之間誤差是一個區(qū)間，這個區(qū)間隨著樣本容量增加精度不斷提高，當(dāng)樣本容量為30時，精度為0.192，樣本量為500時，精度為0.104。總體而言，它們都隨著樣本容量的增加趨向真實(shí)值。

表1 點(diǎn)估計和Bayes估計與參數(shù)真實(shí)值誤差結(jié)果

二項分布的參數(shù)估計在對參數(shù)信息一無所知的情況下，當(dāng)樣本容量較大時，兩種方法對參數(shù)的估計結(jié)果相差很小，并且隨著樣本容量的增加參數(shù)的估計值最終趨向一個穩(wěn)定的數(shù)值，即分布參數(shù)的真實(shí)值。所以單從二項分布的應(yīng)用角度思考，在樣本容量較大和對參數(shù)信息知之甚少的情況下，可以直接用點(diǎn)估計來完成參數(shù)的估計，從而得到估計值。這樣既可以減少計算參數(shù)后驗分布的困難，也可以很快的得到參數(shù)估計結(jié)果。

（作者單位：塔里木大學(xué)信息工程學(xué)院）

塔里木大學(xué)青年創(chuàng)新校長基金（TDZKQN201615）