單點激光連續(xù)掃描測振的薄壁圓筒件模態(tài)測試*

伍濟鋼，袁繼廣，蔣 勉，張雙健

(湖南科技大學機械設備健康維護湖南省重點實驗室 湘潭，411201)

單點激光連續(xù)掃描測振的薄壁圓筒件模態(tài)測試*

伍濟鋼，袁繼廣，蔣 勉，張雙健

(湖南科技大學機械設備健康維護湖南省重點實驗室 湘潭，411201)

針對薄壁圓筒構件模態(tài)測試的需求，提出了基于單點激光連續(xù)掃描測振的薄壁圓筒構件模態(tài)測試方法。根據純模態(tài)分析理論，在研究兩端固定細弦自由振動的基礎上，理論上建立了單點激光測振儀在兩端固定的自由振動細弦上做連續(xù)掃描所得的振動信號和弦的模態(tài)振型之間的關系，研究了并提出了激光測振儀輸出信號的處理方法。搭建了單點激光連續(xù)掃描測振的薄壁圓筒構件模態(tài)測試平臺，對薄壁圓筒構件進行了模態(tài)實測，獲得了薄壁圓筒構件前五階固有頻率和相應的模態(tài)振型，并對測試結果進行了有限元模態(tài)分析驗證。結果表明，模態(tài)振型一致,固有頻率誤差在5%以內，證明了提出方法的正確性和有效性。

單點激光連續(xù)掃描； 振動測量； 薄壁圓筒構件； 模態(tài)測試

引 言

薄壁圓筒構件具有重量輕、材料用量少和結構緊湊等優(yōu)點，廣泛應用于工業(yè)生產各個領域。薄壁圓筒構件剛度較低，在設備運行過程中易產生過度振動形成振動噪聲甚至引起故障，因此必須對薄壁圓筒構件進行模態(tài)測試。

國內外學者對薄壁構件的振動及模態(tài)測量問題進行了大量研究。傳統的采用振動傳感器加力錘錘擊的模態(tài)寬頻測試方法會因粘貼傳感器引入附加質量而改變薄壁構件的模態(tài)，同時存在測點少、空間分辨率低等問題[1-2]。激光測振技術以其非接觸式測量、測量精度高等特點在振動測量中得到了廣泛的應用，解決了傳感器對薄壁構件產生附加質量的問題，同時也沒有安裝空間的限制。Stanbridge等[3]運用多普勒激光測振儀測得了平板的工作振型。Maio等[4]以旋轉的碟式刀片為研究對象，研究了多普勒激光測振儀在旋轉對稱結構工作振型測量上面的應用。盧喜豐等[5]以中空的薄壁長方體模型和白車車身為研究對象，采用單點激光測振儀對其進行試驗模態(tài)分析，得到在固支條件下模型各個面的固有頻率及振型，克服了單頭激光測振系統難于測試三維空間結構模態(tài)的局限性。李旺益等[6]通過對飛機模型純模態(tài)試驗，提出了一種把純模態(tài)試驗理論和激光測振相結合的激光純模態(tài)測試方法。文獻[7-9]設計了試驗平臺，將圓筒固定在帶有旋轉臺的振動臺上，通過旋轉臺的旋轉帶動圓筒結構的轉動，結合激光測振技術，實現了對圓筒結構的工作振型測量，但在測量過程中會引入一些不相干的振動，從而影響振動測試結果。可見，采用先進的激光測振技術進行薄壁圓筒構件的模態(tài)測試是工業(yè)生產的必然需求[10]。

針對薄壁圓筒模態(tài)測試的需求，筆者提出了單點激光連續(xù)掃描測振的薄壁圓筒模態(tài)的模態(tài)測試方法，對薄壁圓筒構件進行高效、高精度和全視野振動測量，實現了薄壁圓筒構件的快速、高精度、高分辨率模態(tài)測試。

1 單點激光連續(xù)掃描測振的薄壁圓筒構件模態(tài)測試原理

1.1 測試方案

如圖1所示，模態(tài)測試系統由4部分組成，分別為薄壁圓筒構件及其懸掛支撐、棱鏡直線和旋轉掃描運動及其控制系統、激光測振儀及其支撐、激振系統。薄壁圓筒構件用4根柔性繩懸掛實現自由支撐，4根柔性繩的固有頻率相對于薄壁圓筒構件的第1階固有頻率要小得多，對測試結果影響非常小。棱鏡直線運動為一套導軌導槽結構，工作時導槽固定，導軌由伺服電機驅動進行移動；棱鏡旋轉運動通過伺服電機旋轉軸上用夾具固定了一45°直角棱鏡實現，以改變激光在薄壁圓筒里的方向，使激光直射到薄壁圓筒的內壁，伺服電機旋轉實現內壁的圓周掃描。激振系統中的振動控制器會產生正弦信號，經功率放大器放大加載到激振器上，帶動薄壁圓筒構件產生同頻振動。同時，激振器的振動信號經加速度傳感器反饋到振動控制器，保證激振器產生激振信號的精度。當伺服電機旋轉時，相應測點的振動由激光測振儀轉化為對應的電壓信號。DAQ采集卡同步采集這一電壓信號，經計算機分析處理得到掃描運動軌跡上的模態(tài)振型。

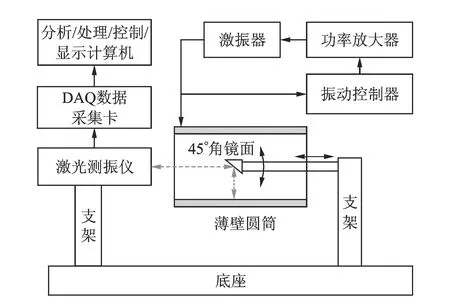
圖1 單點激光連續(xù)掃描測振的薄壁圓筒構件模態(tài)測試方案Fig.1 Modal testing scheme for thin-sheet cylinder parts based on single-point laser continuous scanning vibrometry

1.2 掃描振動信號與模態(tài)振型的關系

激光測振儀掃描的軌跡為薄壁圓筒構件的圓周，根據其起始點可展開成一直線，用激光在兩端固定的自由振動弦上連續(xù)掃描的輸出振動信號來研究與其模態(tài)振型之間的關系。如圖2所示，假設有一根細弦張緊于兩固定點之間，弦的單位長度的質量為ρ(x)，在橫向分布力f(x,t)作用下作橫向振動，張力為T(x,t)，跨長為L，弦x處的橫向位移函數為y=y(x,t)。

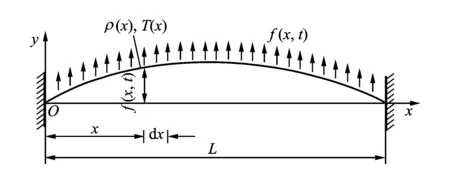
圖2 兩端固定的振動弦Fig.2 Vibrating string with both ends fixed

如圖3所示，取微段弦線單元體dx并假設弦作微小橫向振動，由牛頓定律可得

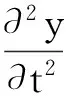
(1)

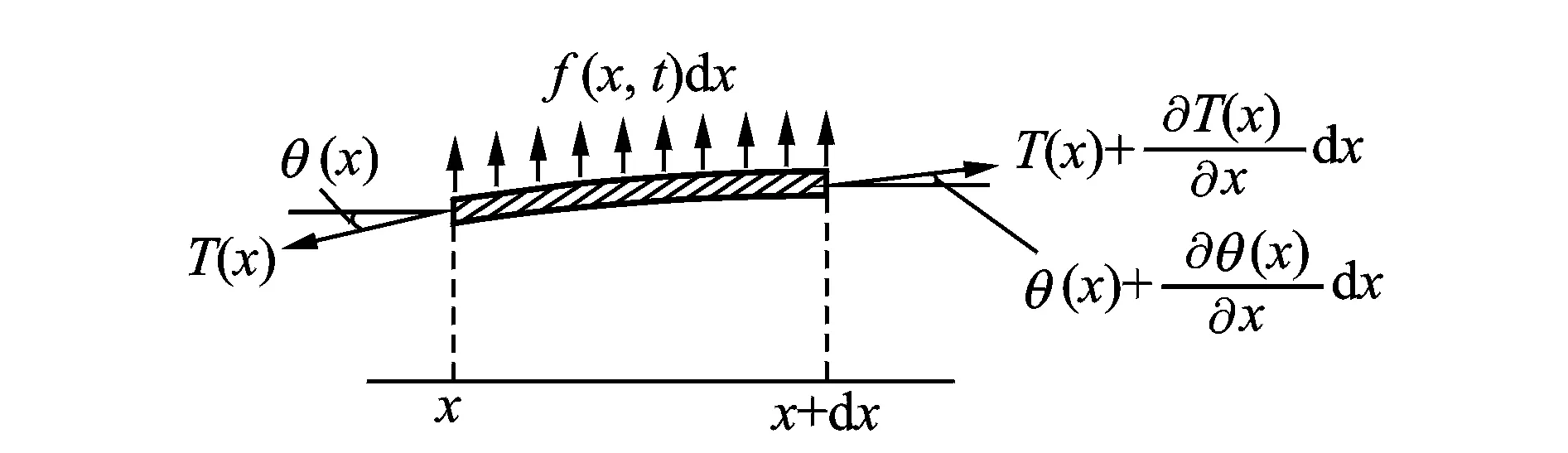
圖3 微段振動弦線Fig.3 Micro section of vibrating string

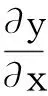
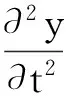
(2)

假設弦的單位長度質量ρ(x)=ρ，并為常數，橫向位移y(x,t)為小量，弦內張力T可以視為常量，則式(2)簡化為

(3)

如果f(x,t)=0，則弦的自由振動微分方程為

(4)

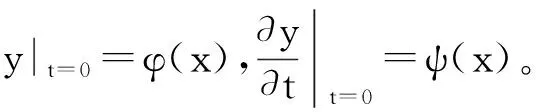
用分離變量法進行求解，得到

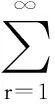
(5)

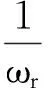
弦的振動為一系列振幅、頻率和相位不同的駐波的疊加，即y(x,t)為弦在某一邊界條件下的振動狀態(tài)，而這一振動是由模態(tài)疊加所得。當激光在振動弦上以恒定速度v做連續(xù)掃描測振時，激光的位置和時間的關系可以用x=vt表示，將其代入式(5)，得到激光在弦上做連續(xù)掃描測振時輸出振動位移的時域信號為

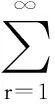
(6)

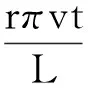
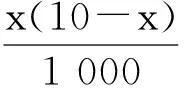
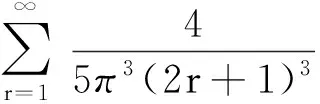
(7)

將x=vt代入式(7)，得到激光測振儀輸出的振動位移時域圖，如圖4所示。當r分別等于1,2,3時，弦的前三階模態(tài)振型和相應的激光測振儀輸出的振動位移時域圖中的上下交替包絡線完全等同于在這一階固有頻率下的模態(tài)振型。這為研究激光連續(xù)掃描測量振動體的模態(tài)振型提供了理論基礎。

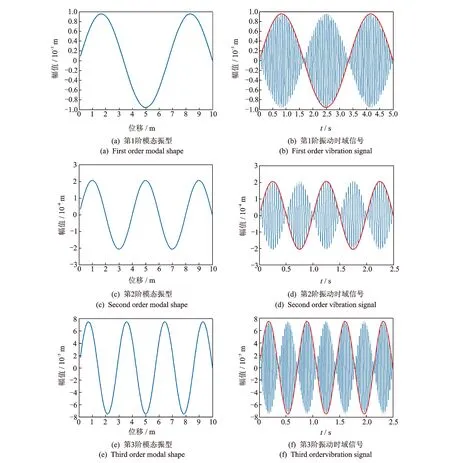
圖4 振動弦前三階模態(tài)振型及其相應的振動時域圖Fig.4 Vibration mode of vibrating string in former three orders and its vibration time domain figures

1.3 激光測振儀的輸出信號處理方法

為了得到測試對象在固有頻率振動下相應的模態(tài)振型，必須對DAQ采集卡采集的激光測振儀的輸出信號進行相應的信號處理。

圖5為信號處理流程圖。由DAQ采集卡輸出的信號為電壓信號，經靈敏度校核處理后轉變?yōu)樗俣刃盘枴Ｔ跍y量過程中信號不可避免地會加入很多噪聲，因此必須對信號進行濾波。由于多普勒激光測振儀測得的電壓信號對應的為振動速度，測試需要的是振動位移信號，因此必須將速度信號轉化成位移信號。經位移信號幅值點的滑動平均，得到位移信號的上下交替包絡線；但這些點構成的包絡線可能會因為測量誤差等因素影響其光滑度，所以還必須進行曲線擬合光滑處理，最后得到固有頻率下的模態(tài)振型。

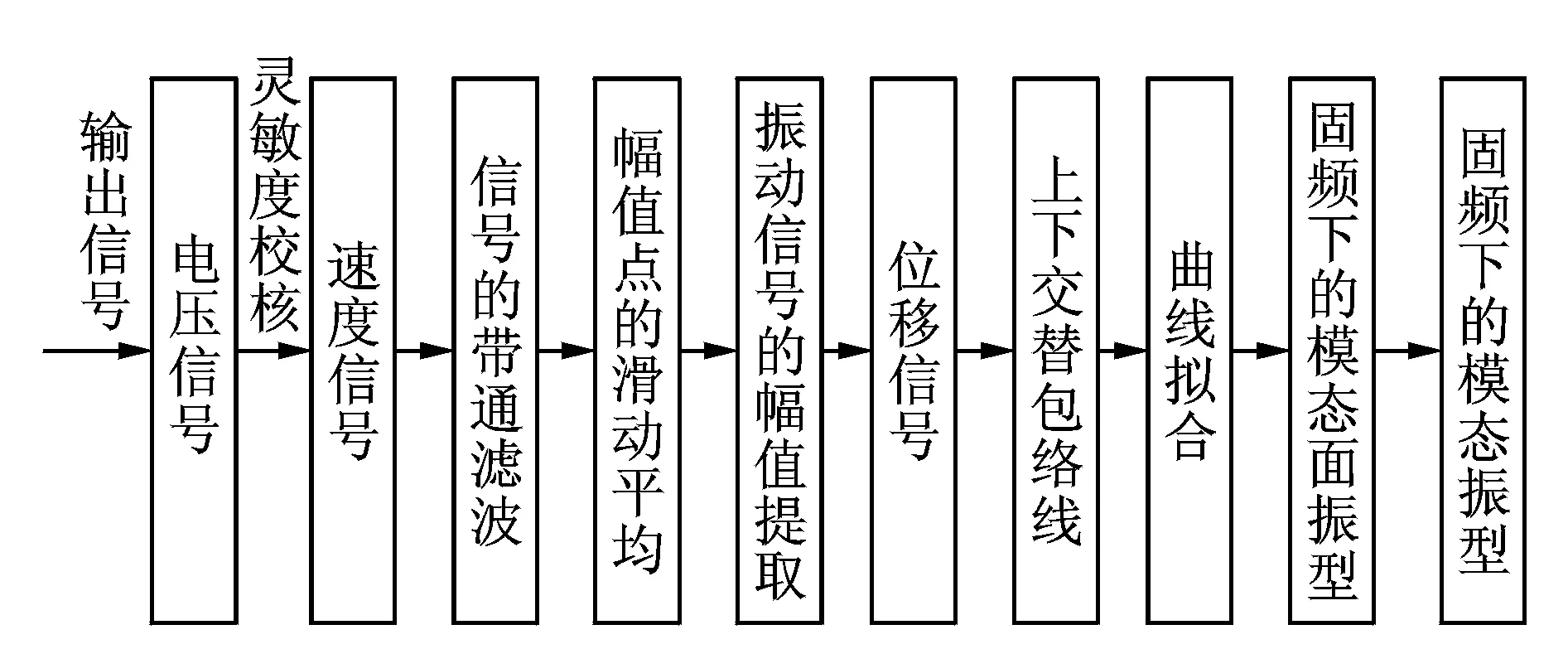
圖5 激光測振儀輸出信號處理工作流程Fig.5 Processing flow chart for outcoming signal of laser vibrometry

振動信號的包絡線其實是振動信號每個周期的幅值點組成的曲線，分為上包絡線和下包絡線。在測試對象由穩(wěn)定正弦激勵信號激振產生的受迫振動中，上下包絡線關于x軸對稱。要求取上下交替包絡線，先找到上包絡線靠近x軸的極小值和下包絡線靠近x軸的極大值作為判斷條件。構造一個新的向量，按條件依次將幅值點賦給此向量，得到向量包含的上下交替包絡線。具體流程如圖6所示。

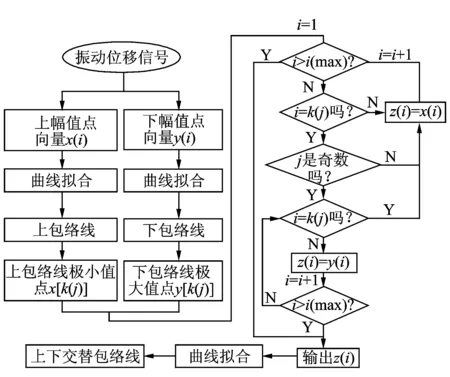
圖6 上下交替包絡線求取的程序流程Fig.6 Calculation flow chart for upper and lower alternate envelope

直角棱鏡的勻速旋轉最終使激光束在薄壁圓筒內表面以恒定的線速度運動，直接獲得的是整個薄壁圓筒構件內壁的模態(tài)振型，還必須將其轉化為真實的薄壁圓筒構件的模態(tài)振型。直角棱鏡的角速度θ與激光束的線速度v的關系為

v=rθ

(8)

其中：r為圓筒的內半徑。

二維平面振型變?yōu)槿S立體振型的公式為

(9)

其中：(xk，yk)為變化后的坐標；Δy為平面振型中每個點所對應的幅值；θ0為激光束在薄壁圓筒構件內壁掃描對應的初始角；Δθ為直角棱鏡旋轉的角度增加量；k為對應的采集點序號。

1.4 激振位置選擇

為了保證系統的可辨識性，一般要求激勵點不應該靠近節(jié)點或者節(jié)線太近。這就要求最佳激勵點的位移響應值不等于零。最佳激勵點定義為

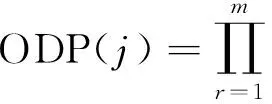
‖φjr‖

(10)

其中：r為模態(tài)階數。

(11)

定義第j個自由度的平均驅動自由度加速度為

(12)

激勵點的選擇應避免選在最佳激勵點的值為零的點。如果在這些點激振，激振力再大，模態(tài)也是很難被激出來。另外，應該選擇自由加速度較大的位置，因為在這些點會導致激振器的附加質量對被測物體影響較大。考慮到各方面因素，激勵點選擇在靠近圓筒一端邊緣上的某個點上[11]。

2 單點激光連續(xù)掃描測振的薄壁圓筒構件模態(tài)實測

2.1 測試平臺的搭建

根據單點激光連續(xù)掃描測振的薄壁圓筒構件模態(tài)測試原理搭建測試平臺，如圖7所示。

圖7 薄壁圓筒構件的模態(tài)測試平臺Fig.7 Modal testing platform for thin-sheet cylinder parts

2.2 測試結果及分析

圖8為薄壁圓筒構件模態(tài)測試掃頻試驗時的激振系統驅動電壓。可以看出，在10～350 Hz之間，薄壁圓筒構件共有5階固有頻率，分別為39.9，123.0，153.9，169.3和293.6 Hz。分別在相應固有頻率下對薄壁圓筒構件進行定頻分析，給激振器施加相應的正弦激勵，可激出各自的模態(tài)振型。通過單點激光連續(xù)掃描測振，獲得相應的振動信號；對振動信號進行處理，獲得每一階頻率下的振型。

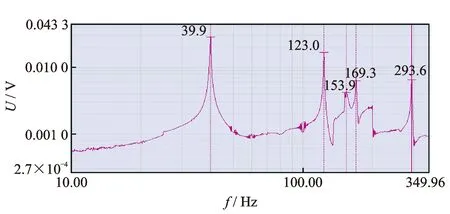
圖8 掃頻試驗中激振系統的驅動電壓Fig.8 Driving voltage of exciting system in in sweep frequency experiments

3 與薄壁圓筒構件有限元模態(tài)分析的對比

薄壁圓筒構件的內直徑為284 mm，厚度為2 mm，高度為80 mm，材料為結構鋼，密度為7 850 kg/m3，彈性模量為2×1011Pa，泊松比為0.3。利用ANSYS軟件，在Workbench中對薄壁圓筒構件進行模態(tài)分析。圖9為薄壁圓筒構件的有限元模型。

圖9 薄壁圓筒構件的有限元模型Fig.9 Finite element model of thin-sheet cylinder parts

表1為有限元模態(tài)分析與模態(tài)實測的固有頻率對比。薄壁圓筒構件有限元模態(tài)分析的前5階固有頻率分別為38.2，117.4，149.9，164.9和280.1 Hz，與模態(tài)實測得到的固有頻率基本相同，誤差保持在5%以內。

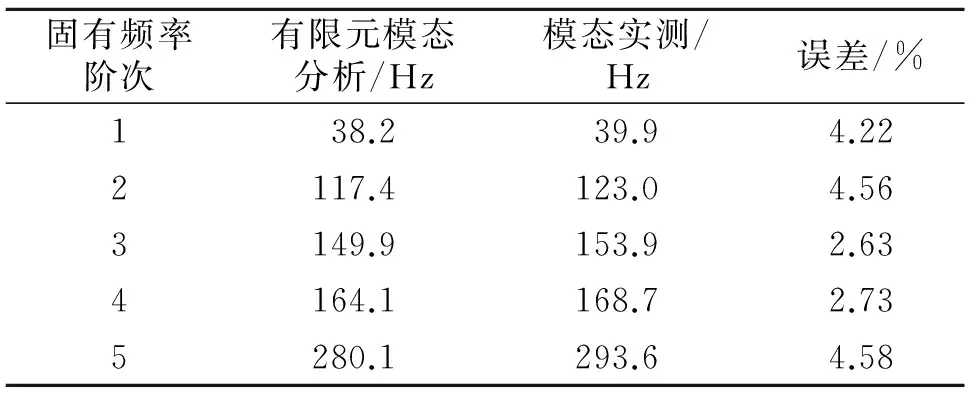
表1 有限元模態(tài)分析與模態(tài)實測的固有頻率對比Tab.1 Results comparison of natural frequency between finite element analysis and experimental test

圖10為薄壁圓筒構件有限元模態(tài)分析和模態(tài)實測的前五階振型對比。可以看出：第1階模態(tài)振型的截面都類似為一橢圓；兩者的第2階振型也類似為一橢圓，同時表現為在“橢圓”的長徑處向外翻轉，短徑處向內翻轉；第3階振型都呈現為類似三菱柱的形狀；兩者的第4階振型除了表現類似三菱柱的形狀外，同時“三菱柱”的邊也都有存在翻轉；第5階振型兩者都呈現四棱柱的形狀。可見，單點激光連續(xù)掃描測振得到的模態(tài)振型和有限元模態(tài)分析得到的模態(tài)振型基本一致，僅存在一些細微的差別，這主要是由于試驗中一些復雜因素在仿真中無法模擬[12]而造成的。

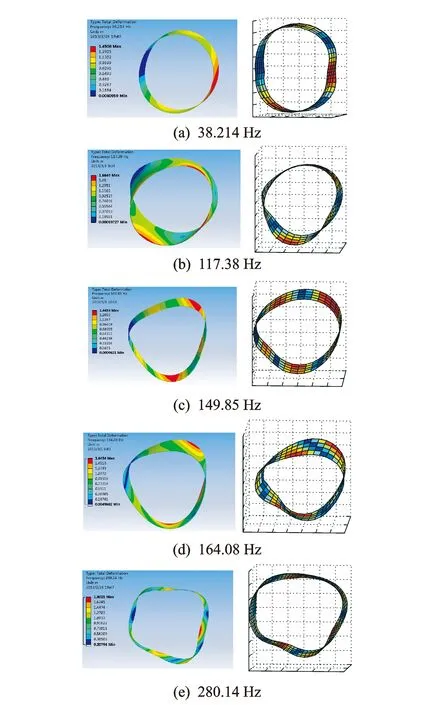
圖10 有限元模態(tài)分析和模態(tài)實測的前5階振型對比Fig.10 Former five order vibration mode comparison between finite element analysis and experimental test

4 結束語

針對薄壁圓筒構件模態(tài)測試的需求，突破了激光連續(xù)掃描測振方法在視角上的制約，提出了薄壁圓筒構件模態(tài)振型的快速、高精度測試方法。根據純模態(tài)分析理論，在研究兩端固定細弦自由振動的基礎上，理論上建立了單點激光測振儀在兩端固定的自由振動細弦上做連續(xù)掃描所得的振動位移信號和弦的模態(tài)振型之間的關系，得出掃描所得的振動時域信號的上下交替包絡線即為掃描路徑的模態(tài)振型的結論。研究了振動信號的處理方法，提出了上下交替包絡線的求取方法。搭建薄壁圓筒構件模態(tài)測試平臺，對薄壁圓筒構件進行模態(tài)測試，獲得薄壁圓筒構件前五階固有頻率和相應的模態(tài)振型，并對測試結果進行有限元模態(tài)分析驗證。固有頻率誤差在5%以內、模態(tài)振型一致，證明了提出方法的正確性和有效性。

[1] 段海洋.薄壁圓柱殼振動特性的研究[D].沈陽:東北大學,2012.

[2] 劉彥琦,褚福磊.幾何參數對旋轉薄壁圓柱殼振動特性的影響[J].振動與沖擊,2012(1):22-25.

Liu Yanqi,Chu Fulei.Effects of geometric parameters on vibration characteristics of rotating thin circular cylindrical shell[J].Journal of Vibration and Shock,2012(1):22-25.(in Chinese)

[3] Stanbridge A B,Martarelli M，Ewins D J.Measuring area vibration mode shapes with a continuous-scan LDV[C]∥Proceedings of the Fourth International Conference on Vibration Measurements by Laser Techniques.Ancona,Italy:International Society for Optics and Photonics，2000,4072:176-183.

[4] Maio D D,Ewins D J.Applications of continuous tracking SLDV measurement methods to axially symmetric rotating structures using different excitation methods[J].Mechanical Systems and Signal Processing,2010,24:3013-3036.

[5] 盧喜豐.實驗模態(tài)分析與激光測振技術研究[D].成都:西南交通大學,2007.

[6] 李旺益.純模態(tài)激光測試法的研究[D].南京:南京航空航天大學,2008.

[7] Daborn P M，Ind P R，Ewins D J.Enhanced ground-based vibration testing for aerodynamic environments[J].Mechanical Systems and Signal Processing,2014(49):165-180.

[8] Giuliani P，Maio D D，Schwingshackl C W,et al.Six degrees of freedom measurement with continuous scanning laser doppler vibrometer[J].Mechanical Systems and Signal Processing,2013(38):367-383.

[9] Zucca S,Maio D D,Ewins D J.Measuring the performance of underp latform dampers for turbine blades by rotating laser Doppler vibrometer[J].Mechanical Systems and Signal Processing,2012(32):269-281.

[10]肖良瑜,李建偉,宋大鳳,等.立式屏蔽電機半速渦動異常振動試驗分析[J].振動、測試與診斷,2015,35(2):316-321.

Xiao Liangyu,Li Jianwei,Song Dafeng,et al.Analysis of abnormal vibration of half speed eddy for vertical canned motor[J].Journal of Vibration,Measurement &Diagnosis,2015,35(2):316-321.(in Chinese)

[11]賀良國,劉永斌,張連生,等.基于壓電激振的彈性模量測量方法[J].振動、測試與診斷,2014,34(6):1080-1083.

He Liangguo,Liu Yongbin,Zhang Liansheng,et al.Research on measuring method of elastic modulus by piezoelectric excitation resonance[J].Journal of Vibration,Measurement &Diagnosis,2014,34(6):1080-1083.(in Chinese)

[12]田永衛(wèi),閆楚良,張書明,等.飛機隨機振動環(huán)境實測試驗數據的歸納方法[J].振動、測試與診斷,2014,34(6):1129-1133.

Tian Yongwei,Yan Chuliang,Zhang Shuming,et al.Inductive method of flight test data measured from aircraft random vibration environment[J].Journal of Vibration,Measurement &Diagnosis,2014,34(6):1129-1133.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.04.007

* 國家自然科學基金資助項目(51205122)

2015-06-10；

2015-08-24

TH113.1

伍濟鋼，男，1978年8月生，博士、副教授。主要研究方向為機械動力學和機器視覺測量等。曾發(fā)表《Rotor crack fault diagnosis based on base and multi-sensor adaptive weighted information fusion》(《Journal of Software》2012,Vol.7,No.7)等論文。 E-mail：jgwu@foxmail.com