基于連續(xù)行走的人行荷載模型參數實驗*

朱前坤，劉路路，杜永峰，李宏男，陳 凱

(1.蘭州理工大學防震減災研究所 蘭州，730050)(2.大連理工大學建設工程學部 大連，116024)(3.東南大學土木工程學院 南京，210096)

基于連續(xù)行走的人行荷載模型參數實驗*

朱前坤1,2，劉路路3，杜永峰1，李宏男2，陳 凱1

(1.蘭州理工大學防震減災研究所 蘭州，730050)(2.大連理工大學建設工程學部 大連，116024)(3.東南大學土木工程學院 南京，210096)

為建立人行荷載的傅里葉級數模型，采用新型微電子機械系統(tǒng)AH100B加速度傳感器得到201人次、1 407條連續(xù)行走在樓板上的荷載曲線。根據姿態(tài)角形成的姿態(tài)矩陣可將載體坐標系下的三軸加速度轉換到自然坐標系下，通過快速傅里葉變換計算人行荷載縱向、側向和豎直方向前4階動力荷載因子及相位角，得出用于解決結構振動舒適度問題的三向傅里葉級數荷載模型。采用小波變換得到單條荷載曲線的時頻圖，反映出單人在行走過程中行走頻率的變異性。將荷載模型與已有的其他模型進行比較，驗證了荷載模型的合理性及可行性，為解決大跨度結構人行激勵產生的振動問題提供了參考。

人行激勵； 姿態(tài)轉換矩陣； 傅里葉級數荷載模型； 動力荷載因子； 小波變換

引 言

由于施工、設計方法的進步和高強度輕質材料的廣泛使用，使結構的跨度越來越大。這些結構在人群荷載的作用下會引發(fā)水平或豎向振動。過大的振動會影響結構的正常使用[1-2]，嚴重時會引發(fā)結構破壞，造成人員傷亡。因此，人行荷載作用產生的振動問題成為大跨結構設計中必須考慮的一個主要因素[3]。

人的步行、跳躍和跑動等活動對結構產生的作用稱為人致激勵，在人致激勵作用下對結構產生的動力響應稱為人致振動[4]。其中，由步行荷載引起的結構振動最常見。對人致激勵的研究最早起源于1977年，Blanchard等[5]在關于人行橋動力激勵中提出了一個簡單的正弦激勵荷載模型。Kerr等[6]、Vitomir等[7]采用測力板和跑步機得到連續(xù)人行荷載曲線。文獻[8-9]利用加速度采集儀得到三向加速度，所得加速度均為人行走時動態(tài)坐標軸上的取值，未轉換到自然坐標系下。陳雋等[10]利用三向測力板及三維動作捕捉技術給出三向單足落步荷載實驗模型，根據步行時間將其拓展成連續(xù)的荷載曲線[11]，但因存在拓展時左右腳荷載完全相同的假設，故與實際人行荷載時程不能完全符合。在考慮人-結構相互作用的基礎上，Da Silva等[12]采用質量-剛度-阻尼生物力學模型代替人群行為，仿真結果與實驗結果較為接近。

筆者通過采用新型微電子機械系統(tǒng)(micro electronic mechanical system,簡稱MEMS)AH100B傳感器測定人行走在樓板上的三軸加速度。基于牛頓第二定律得到連續(xù)的三向荷載曲線，形成單人連續(xù)行走作用下的傅里葉級數荷載模型。將其與國內外其他荷載模型進行比較，驗證了筆者提出的荷載模型的合理性及可行性。

1 人行荷載動力特性實驗

1.1 實驗設備

如圖1所示，AH100B加速度傳感器是一款體積超小、高精度和高性能的慣性姿態(tài)測量系統(tǒng)，配備高精度三軸陀螺傳感器、三軸加速度傳感器和三軸磁場傳感器，可以測量靜止狀態(tài)或運動狀態(tài)下載體的三向加速度和姿態(tài)角(橫滾角γ、俯仰角θ及航向角φ)。

圖1 加速度傳感器Fig.1 Acceleration sensor

1.2 實驗步驟

由于混凝土結構應用的廣泛性及普遍性，本次實驗是在某大跨混凝土樓板上開展的。為獲得大量的實驗數據、減少實驗誤差、保證數據的精確性以及可靠性，本次實驗完成了對201名在校學生的人行荷載實驗。表1為測試者的基本信息。

MEMS加速度傳感器固定在人體質心部位，由文獻[12-13]可知，女性質心位置為0.55h，男性為0.57h(h為人體高度)。為保證數據的可靠性，本實驗采用在每個測試者質心位置前后固定兩個傳感器，取平均值作為一次實驗獲得的連續(xù)荷載時程，實驗情況如圖2所示。每位測試者被要求完成7組步行實驗，包括3組慢速、中速和快速的自由行走以及4組分別為1.7，1.85，2.10和2.35 Hz的固定步行頻率實驗。固定頻率步行是指測試者在電子節(jié)拍器的導引下，根據聲響踏節(jié)拍完成。

表1 測試者基本信息Tab.1 The basic information of testers

圖2 實驗測試者Fig.2 Experimental tester

1.3 自然坐標系與載體坐標系

對人體建立載體坐標系O-x′y′z′或稱動態(tài)坐標系和自然坐標系O-xyz。在載體坐標系O-x′y′z′，無論人處于靜止還是運動狀態(tài)，始終取人體冠狀面法向向前為x′軸正方向，矢狀面法向向左為y′軸正方向，水平面法向向下為z′軸正方向。對于自然坐標系O-xyz中，人體豎直站立，取人體冠狀面法向向前為x軸正方向即人行走縱向，矢狀面法向向左為y軸正方向即人行走側向，水平面法向向下為z軸正方向即人行走豎直方向[14]。在人體豎直站立時，x′軸、y′軸、z′軸構成的左手坐標系與自然坐標系完全重合。將加速度傳感器佩戴在測試者質心處時，其3個坐標系方向與規(guī)定的載體坐標軸重合[14]。因此，傳感器3個軸向加速度輸出(ax′,ay′,az′)即為載體坐標系下3個軸向加速度分量。人體步行運動時，載體坐標與緊貼在人體的傳感器一塊隨著載體的運動而運動，此時載體坐標系不再與自然坐標系重合。任意時刻的載體坐標系都可由原點相同的自然坐標系經3次旋轉得到，如圖3所示。

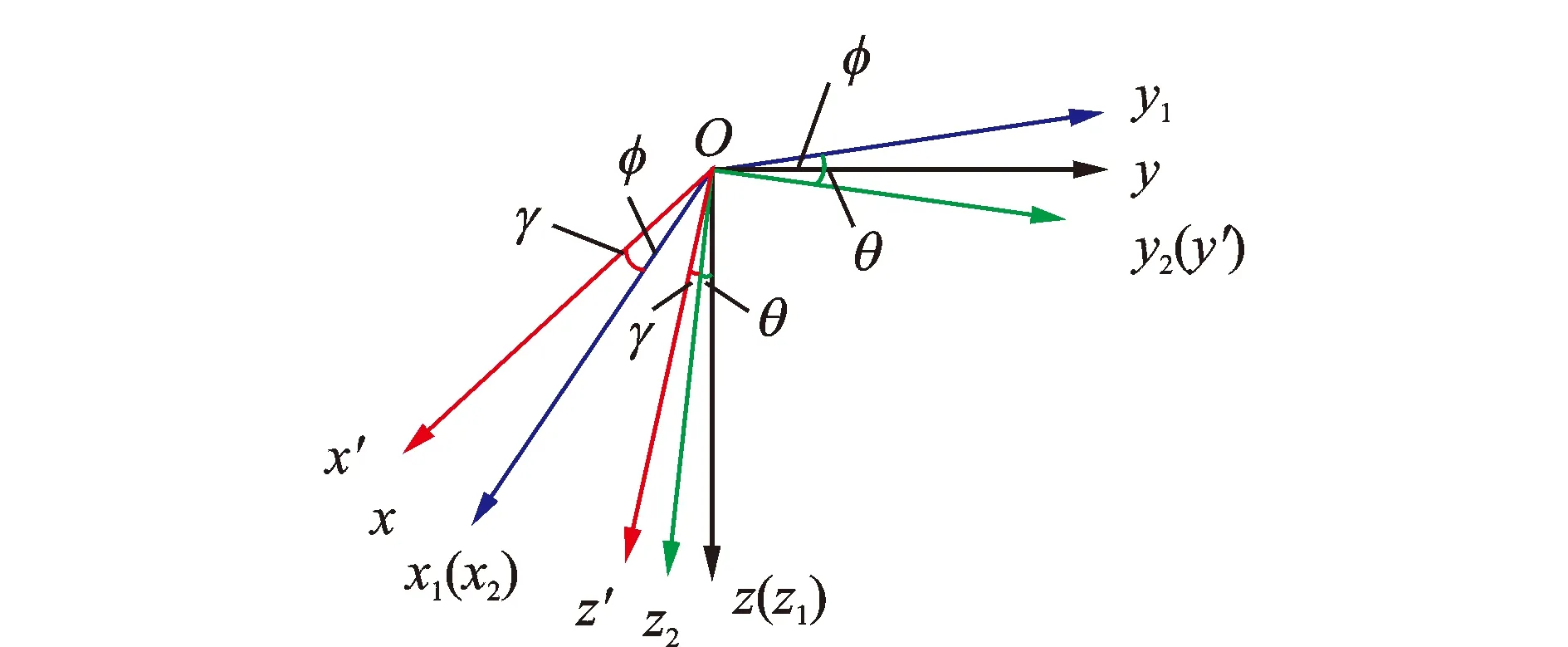
圖3 自然坐標系與載體坐標系Fig.3 Natural and carrier coordinate systems

實驗目的是為得到自然坐標系下人行荷載曲線，故將動態(tài)坐標系下采集到的加速度利用姿態(tài)矩陣T轉換到自然坐標系下，如式(1)[15]所示。

(1)

其中：γ，θ，φ分別為MEMS加速度傳感器內置九軸運算解得的橫滾角、俯仰角和航向角；ax′，ay′，az′為MEMS加速度傳感器采集到的加速度；ax，ay，az為經過姿態(tài)矩陣變換之后自然坐標系下的加速度。

1.4 實驗結果

完成201人次的行走激勵實驗，每個人對應7種行走工況，共得到平均之后的1 407組荷載曲線。圖4為某男性測試者(身高為175 cm，體重為74 kg)在中速自由行走工況下的三向加速度時程曲線。其中，ax，ay，az分別為行走時x向、y向以及z向(含重力加速度g)的加速度值。虛線為加速度傳感器直接采集到的加速度時程，即轉換前加速度時程；實線為經過姿態(tài)矩陣T轉換到自然坐標系下的加速度時程曲線，即轉換后加速度時程。圖4表明，z向兩曲線基本重合，x向及y向轉換前后略有差異。這是因為佩戴在人體的加速度傳感器會隨著載體的運動在水平面內發(fā)生微小的轉動，但在豎向幾乎沒有轉角。顯然，圖4與實際情況相符，證明了其合理性。

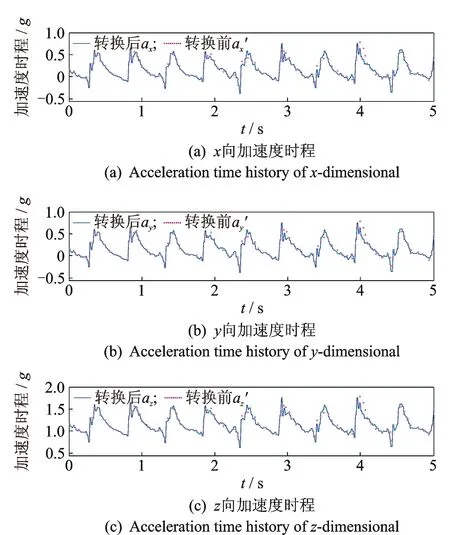
圖4 三向加速度時程曲線Fig.4 Three-dimentional acceleration time history

2 人行荷載的模型

2.1 傅里葉級數模型

縱向Fx(t)、側向Fy(t)和豎直方向Fz(t)三向連續(xù)步行荷載在時域上表示為傅里葉級數的形式[10]

(2)

(3)

(4)

其中：G為人體重量；αxi，αyi和αzi分別為x向、y向和z向第i階諧波的動載系數，也常稱為動力荷載因子或稱動載因子(dynamic loading factor，簡稱DLF)；fp為人體行走頻率；φxi，φyi和φzi分別為x向、y向和z向第i階諧波相位角；n為模型中考慮的階數。

2.2 動載因子取值

DLF的定義為步行荷載傅里葉幅值譜峰值與人體體重之比[4]。在本研究中，根據傅里葉變換的線性特性可知，F(ωi)=ma(ωi)，所以直接對傳感器采集到的加速度時程進行傅里葉變換得到步頻及其倍頻處的譜值即為動載因子。圖5為一組三向荷載時程曲線對應的傅里葉頻譜圖(行走頻率fp=1.98 Hz，G=74 kg)。

圖5表明，x向及z向的動載因子峰值一般均在主諧波頻率處出現；但y向由于步行時的前后擺動使動載因子峰值不僅在主諧波頻率處出現，在次諧波頻率處同樣也會出現，且次諧波分量占有很大比重。人行荷載的主要振動頻率分量在10 Hz內，而大跨樓板一般為低頻結構，故進一步證實了人群荷載作用下大跨度結構存在舒適度問題。

大量相關研究表明，DLF大小取決于步行頻率[6]，故對各階DLF與步行頻率的關系進行擬合，找出其關系表達式。對于本次實驗統(tǒng)計的結果，采用多項式擬合時，在一定范圍內，階數越高，其R2越高，擬合效果較精確。但由于精度提高相對較少，所以為計算方便多采用線性多項式擬合(95%的保證率)。對于z向第1階DLF與頻率的非線性關系，參考文獻[6]采用三次多項式擬合的方法,筆者對于z向第1階DLF隨頻率的分布也采用三次多項式進行擬合(R2=0.219)。圖6為自由行走工況下慢、中、快動載因子隨頻率變化的散點圖及擬合曲線。由于篇幅限制，x向和y向只給出了第1階，z向給出了前2階DLF隨頻率變化的散點圖。可見，除第1階DLF表現出與步頻有明顯的相關關系外(隨步頻的增加而變大)，其余各階DLF分布具有較大的離散性。圖6(a)中y向第1階DLF以0.065為基準線均勻分布，最大值可達到0.15左右，且側向荷載分量較多，所以對側向約束比較弱的大跨度樓板，在人群荷載的作用下，其側向振動應給予重視。

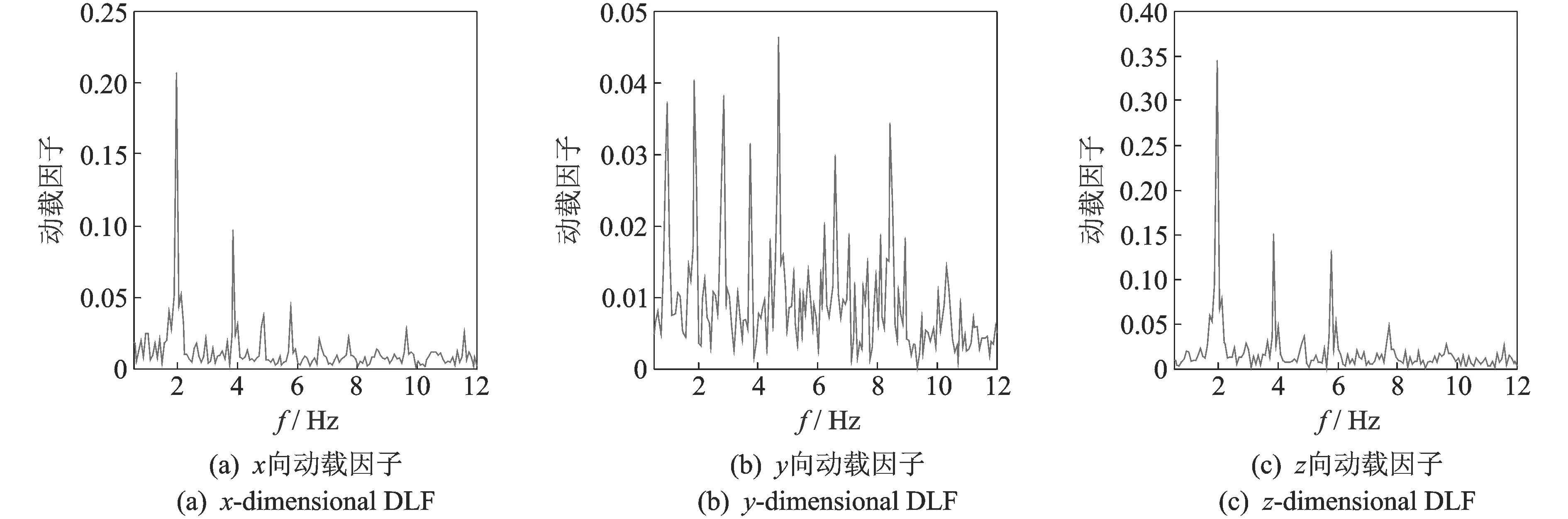
圖5 三向動載因子Fig.5 Three dimensional DLF

圖6 三向動載因子分布散點圖Fig.6 Three-dimensional dynamic load factor distribution scatterplot

圖7為y向以及z向前2階動載因子的分布直方圖及擬合曲線。因DLF分布的離散性，各階DLF的頻數分布直方圖并不是完全服從正態(tài)分布。從其擬合曲線的相關性來說：三向第1階DLF分別大致服從正態(tài)分布，其他階DLF大致呈對數正態(tài)分布。

圖7 三向DLF分布直方圖及擬合曲線Fig.7 Histogram and curve fitting of three-dimensional DLF

表2為自由行走工況下三向動載因子DLF擬合表達式。表3為三向各階動載因子的平均值及標準差，可方便設計人員使用。可以看出，三向荷載的動載因子隨著行走頻率的加快會有增大的趨勢，這與文獻[16]的研究結果類似。x向及z向第1階荷載諧波分量所占比重較大，即取前3階或者4階諧波荷載便可精確描述縱向及豎直方向的人行激勵；但y向前幾階諧波均對荷載模型有很大貢獻，故階數n≥5才能使傅里葉級數荷載模型能夠很好地表示側向人行激勵。

2.3 相位角取值

對荷載時程曲線進行快速傅里葉變換得到相位譜。為了反映出行走過程中相位角的真實變化情況，采用unwrap函數對各階諧波的相位角進行修正。結果表明，無論是x向、y向還是z向，其相位譜都非常離散，現有的實驗研究成果也與此相同，一般不作統(tǒng)計或者取其平均值[7]。圖8為y，z兩向相位譜。對于相位角的取值，根據實驗數據統(tǒng)計出三向各階相位角平均。

x向前4階相位角取值分別為π/6，π/6，-π，-π/2；y向前4階主諧波分量和4個次諧波分量分別為0，0，π/6，π，π/2，0，-π/2，0；z向前4階相位角取值分別為π/2，-π/2，-π/6，-π/6。

表2 三向各階DLF擬合表達式Tab.2 The value of three-dimensional DLF

表3 三向各階DLF均值±標準差Tab.3 Mean±standard deviation of three-dimensional DLF

圖8 荷載相位譜Fig.8 Loading phase spectrums

2.4 小波變換識別個人行走頻率的變異性

傅里葉變換確定的是整個時間域上的頻率特性，沒有局部化分析信號的能力[17]。為識別單個人行走過程中頻率的變異性，采用小波變換，選用morlet小波基，得到單個信號的時頻圖[18]。圖9為利用小波變換對自由行走(fp=1.98 Hz)的y向及z向兩條荷載時程進行小波變換得到的小波時頻圖。可以看出：z向荷載的信號成分比較單一，且第1諧波所占成分較大；y向荷載包含了多種頻率的信號，且前幾階諧波均對傅里葉級數荷載有貢獻，這與采用傅里葉變換得出的結論一致(圖5(b))。小波時頻圖可以反映出單個人在行走過程中行走頻率隨時間的微小變化，這為后續(xù)分析單人行走荷載的動力特性提供了方法指導，并為人與結構相互作用時建立單人的SMD模型提供了基礎。

圖9 小波時頻圖Fig.9 Wavelet time-spectrum plot

3 實驗模型驗證

為驗證本次實驗模型的準確性，選取5種國內外學者[6,10,19-21]研究的z向傅里葉荷載模型與本荷載模型進行比較，如圖10所示。統(tǒng)計本次實驗數據：行走頻率服從fp=normrnd(1.93,0.192)的正態(tài)分布，人體重量服從m=normrnd(64.3,10.64)的正態(tài)分布，故取fp=1.93 Hz，m=64 kg為例進行作圖比較。以往研究大多只給了動載因子取值，沒有給出相位角取值或對相位角提及較少。從傅里葉級數荷載模型的構成項來看，相位角對荷載的計算影響很大。為比較方便，圖中除文獻[10]荷載模型的前4階相位角取值為-π/4，0，0，π/4外，其他模型前4階相位角均取本次實驗的統(tǒng)計值π/2，-π/2，-π/6，-π/6。通過比較發(fā)現，筆者提出的荷載模型與其他荷載模型吻合較好。在峰值上與典型的Kerr模型相比，相差較小，只是波谷比其略低。與文獻[10]的荷載模型相比，波峰與波谷值均比其略偏高。因此，采用本載荷模型用于大跨結構的人行荷載進行計算時，設計結果偏安全。國內外學者對x向與y向荷載模型的研究較少，故筆者沒有作比較。圖11為x向和y向傅里葉級數荷載模型。由于相位角的分散性，降低了傅里葉級數描述實際荷載的精準性。

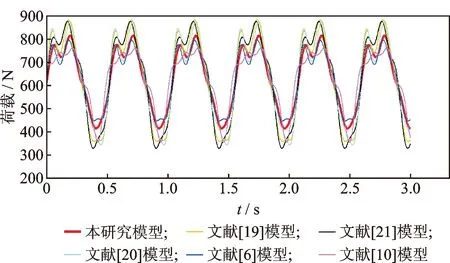
圖10 z向荷載模型比較Fig.10 Comparation of z-dimensional load models

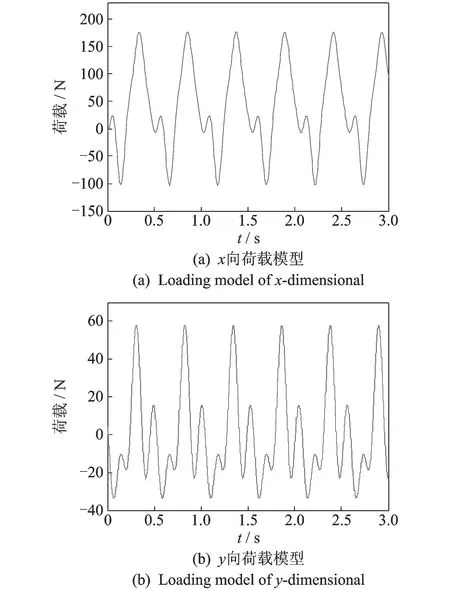
圖11 傅里葉級數荷載模型Fig.11 Fourier series loading models

4 結 論

1) 本研究中的人行荷載實驗是在大跨度混凝土樓板上開展的，故建立的人行荷載模型可以精準描述混凝土樓板上的荷載特性。對于其他結構型式的樓板，例如鋼結構樓板及鋼-混組合樓板，考慮其動力學特征的不同，其荷載模型參數不同，但可以將本荷載模型作為參考。

2) 因側向荷載包括較多頻率成分的振動分量，故在人群荷載作用下容易引發(fā)結構的舒適度問題。對于側向約束比較弱的樓板，例如人行橋或者過人天橋的振動問題，應予以重視。

3) 研究發(fā)現，相位角對荷載模型的建立有很大影響，不僅影響荷載的取值，還影響荷載的形狀曲線。由于相位角的離散性，難以用傅里葉級數荷載模型精確描述人行激勵，所以有關傅里葉荷載模型相位角的分析還需進一步研究。

4) 筆者提出的荷載模型參數為考慮人與結構的耦合作用而建立質量-剛度-阻尼生物力學模型提供了基礎。

[1] HIVOSS.Design of footbridges guideline human induced vibrations of steel structures[M].European Commission:RFCS Publications,2008:48-51.

[2] Dallard P,Fitzpatrick T,Flint A,et al.The London millennium footbridge[J].Structural Engineer,2001,79(171):17-33.

[3] 馮鵬,金飛飛,葉列平,等.人行天橋結構振動舒適度定量化與振動特性實測研究[J].振動工程學報,2013,26(4):545-553.

Feng Peng,Jin Feifei,Ye Lieping,et al.Study on quantization and the measured vibration characteristics of the footbridge structural vibration comfort[J].Journal of Vibration Engineering,2013,26(4):545-553.(in Chinese)

[4] 陳雋,彭怡欣,王玲.基于步態(tài)分析技術的三向單足落步荷載曲線試驗建模[J].土木工程學報,2014,47(3):79-87.

Chen Jun,Peng Yixin,Wang Ling.Experimental investigation and mathematical modeling of single footfall load using motion capture technology[J].China Civil Engineering Journal,2014,47(3):79-87.(in Chinese)

[5] Blanchard J,Davies B L,Smith J W.Design criteria and analysis for dynamic loading of footbridges[C]∥Proceedings of the DOE and DOT TRRL Symposium on Dynamic Behaviour of Bridges.Crowthorne,UK:[s.n.],1977:90-106.

[6] Kerr S C,Bishop N W P.Human induced loading on flexible staircases[J].Engineering Structures,2001 (23):37-45.

[7] Vitomir R,James M,William B.Stochastic model of near-periodic vertical loads due to humans walking[J].Advanced Enginerring Informatics,2011,25(2):259-275.

[8] 李紅利.基于響應譜方法的人行橋人致振動響應研究[D].湖南:湖南大學,2013.

[9] 李紅利,陳政清.人-橋豎向動力相互作用效應理論與試驗研究[J].土木工程學報,2014,47(6):78-87.

Li Hongli,Chen Zhengqing.Analytical and experimental study on vertically dynamic interaction between human and bridge[J].China Civil Engineering Journal,2014,47(6):78-87.(in Chinese)

[10]陳雋,王浩琪,彭怡欣.行走激勵的傅里葉級數模型及其參數的實驗研究[J].振動與沖擊,2014,33(8):11-15,28.

Chen Jun,Wang Haoqi,Peng Yixin.Experimental investigation on Fourier-series model of walking load and its coefficients[J].Journal of Vibration and Shock,2014,33(8):11-15,28.(in Chinese)

[11]陳雋,葉艇,彭怡欣.拓展步行荷載對樓板振動響應影響的對比研究[J].振動與沖擊,2012,31(18):55-59.

Chen Jun,Ye Ting,Peng Yixin.A comparison study on methods for expanding a single foot-falling load curve based on floor responses[J].Journal of Vibration and Shock,2012,31(18):55-59.(in Chinese)

[12]Da Silva F T,Brito H M B F,Pimentel R L.Modeling of crowd load in vertical direction using biodynamic model for pedestrians crossing footbridges[J].Canadian Journal of Civil Engineering,2013,40(12):1196-1204.

[13]Bartlett R.Introduction to sports biomechanics[M].Great Britain:Alden Press,1977:289.

[14]曹玉珍,蔡偉超,程旸.基于MEMS加速度傳感器的人體姿態(tài)檢測技術[J].納米技術與精密工程,2010,8(1):37-41.

Cao Yuzhen,Cai Weichao,Cheng Yang.Body posture detection technique based on MEMS acceleration sensor[J].Nanotechnology and Precision Engineering,2010,8(1):37-41.(in Chinese)

[15]李路.基于多傳感器的人體運動模式識別研究[D].濟南:山東大學,2013.

[16]Rainer J H,Pemica G,Allen D E.Dynamic loading and response of footbridges[J].Canadian Journal of Civil Engineering,1988(15):66-71.

[17]Zivanovic S,Pavie A,Reynolds P.Probability-based prediction of multi-mode vibration response to walking[J].Engineering Structures,2007,29(6):942-954.

[18]伊廷華，李宏男，王國新.基于小波變換的結構模態(tài)參數識別[J].振動工程學報,2006,19(1):51-56.

Yi Tinghua,Li Hongnan,Wang Guoxin.Structural modal parameter identification based on wavelet transform[J].Journal of Vibration Engineering,2006,19(1):51-56.(in Chinese)

[19]Willford M R,Young P.Improved methodologies for the prediction of foot-fall induced vibration[M].Paris:Mill Press,2005:1-12.

[20]Bachmann H,Ammann W.Vibration in structures:induced by man and machines[J].Canadian Journal of Civil Engineering,1987,15(6):1086-1087.

[21]Pedersen L,Frier C.Sensitivity study of stochastic walking load models[C]∥Proceedings of the 28th International Modal Analysis Conference.Jacksonville:[s.n.],2010:163-170.

10.16450/j.cnki.issn.1004-6801.2017.04.012

* 國家自然科學基金資助項目(51668042,51508257)；教育部長江學者創(chuàng)新團隊資助項目(IRT13068)；甘肅省高等學校科研資助項目(2015B-34)

2015-09-15；

2015-12-11

TU312+.1； TH825

朱前坤，男，1981年 4月生，博士、副教授。主要研究方向為大跨結構的振動舒適度評估及工程結構振動控制。曾發(fā)表《不同行走步速下人行橋振動舒適度定量化評估》(《工程力學》2016年第33期)等論文。 E-mail：zhuqk@lut.cn