再入飛行器的RCS控制系統設計①

郭建國，張添保，周 軍，王國慶

(1.西北工業大學，精確制導與控制研究所，西安 710072；2.中國運載火箭技術研究院研發中心，北京 100076)

再入飛行器的RCS控制系統設計①

郭建國1，張添保1，周 軍1，王國慶2

(1.西北工業大學，精確制導與控制研究所，西安 710072；2.中國運載火箭技術研究院研發中心，北京 100076)

針對再入飛行器初始再入段的發動機反作用控制系統(RCS)控制精度問題，提出了一種新型發動機控制方法。首先，將飛行器模型分為慢回路和快回路分別進行控制器設計，采用非線性干擾觀測器(DOB)來獲取不確定項的估計值，并使用反演法及滑模控制方法設計了飛行器的慢回路和快回路控制律；其次，采用線性規劃方法來獲取最優RCS指令分配方案；在此基礎上，對傳統PWPF調制器進行改進，提出了積分補償型PWPF調制器(IPWPF)，采用描述函數法證明了該IPWPF的調制穩定性；最后，通過仿真驗證了該方法相比于傳統的控制方法具有較高的控制精度。

再入飛行器；反作用控制系統；干擾觀測器；滑動模態；脈沖調制器

0 引言

再入飛行器飛行包線大、航程遠[1]。再入飛行初期，由于空氣稀薄，需采用RCS控制[2-3]；再入段中期，氣動舵面能夠提供一定的控制力矩，但控制效率較低，一般采用RCS/氣動復合控制[4-5]；再入段末期，空氣比較稠密，可單獨采用氣動控制。本文研究再入飛行初期的RCS控制問題。

再入飛行器RCS的推力大小和方向不可調節，只能提供脈沖式控制量，而控制律提供的是連續控制信號。RCS噴氣邏輯的設計是RCS控制的一大關鍵問題，國內外常用的方法是采用脈沖寬度調制器(PWM)來進行擬線性跟蹤控制。然而傳統的PWM只能調制脈沖寬度。為了使調制器既能調制脈沖寬度，又能調制頻率，一些學者對傳統的PWM進行了改進，提出了脈寬——頻率調制器(PWPF)[5-6]。但是PWM和PWPF均只考慮了輸入信號的大小與輸出信號的脈沖寬度及頻率，而沒有考慮擬線性跟蹤的精度問題。本文在PWPF的基礎上，對其進行改進，提出了一種積分補償型調制器(IPWPF)，使其對信號的復現精度更高。

控制律的設計也是飛行器控制系統設計的一大關鍵問題。目前常用的控制方法有PID控制方法[7]、滑模控制方法[8-11]、魯棒控制方法[12]和自適應控制方法[13]。由于再入飛行器模型具有強耦合、強非線性和快時變特性，PID控制方法很難滿足魯棒性要求；而魯棒控制方法和自適應方法設計較為復雜，工程實現困難，故而滑模控制方法被廣泛運用。本文采用滑模變結構控制思想設計了再入飛行器的控制律。對于飛行器模型中不確定項，采用非線性干擾觀測器(DOB)[14-15]來進行估計。

RCS一般采用冗余噴管配置方案，其數目遠大于飛行器自由度數目，為一個過驅動控制系統[16]。能完成同樣的控制任務的推力器組合不止一種，而需尋求一種既能使控制精度最好，又能節省的控制組合。本文采用線性規劃[1,17]的方法來進行推力器組合控制的優化分配。

1 再入飛行器運動模型

在文獻[18]的基礎上，可得再入初期飛行器運動方程：

(1)

式中Ω=[φV,β,α]T為飛行器的傾側角、側滑角和攻角；ω=[ωx,ωy,ωz]T為飛行器的滾轉角速率、偏航角速率和俯仰角速率；M為RCS提供的控制力矩；f和φ為不確定項；非線性項g(ω)=I-1ω×(I·ω)；A、B、I為系數矩陣。

本文研究10推力器RCS，其在機尾的布局見圖1。

RCS控制系統的模型為

M=MRCSσ

(2)

其中

(3)

式中σ=[σ1,σ2,…,σ10]T為推力器的開啟邏輯，σi=[0,1],i=1,2,…,10。

飛行器再入初期運動方程為

(4)

2 控制系統設計

2.1 非線性干擾觀測器

飛行器飛行時，受到各種不確定項的作用，其中包括參數不確定和外部干擾。對這些不確定項，可采用干擾觀測器(DOB)[19]對不確定項進行估計。含不確定項的飛行器的運動方程如式(4)所示。

(5)

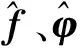
(6)

式中d1=2δf/min(λ1i)，d2=2δφ/min(λ2i)，i=1,2,3。

2.2 控制律設計

設Ωc=[φVc,βc,αc]T為指令信號，將飛行器控制系統分為慢回路和快回路進行設計。利用滑模控制方法，采用反演法[21]獲取姿態角速率指令ωc作為快回路的虛擬控制信號，ωc=[ωxc,ωyc,ωzc]。設：

e1=Ωc-Ω

(7)

e2=ωc-ω

(8)

對式(7)和式(8)求導得

(9)

(10)

取慢回路滑模面為

s1=e1

(11)

式中s1=[s11,s12,s13]T。

采用指數趨近率：

(12)

式中K1=diag(k11,k12,k13),ε1=diag(ε11,ε12,ε13)，且有k1i>0,ε1i>d1,i=1,2,3。

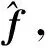
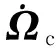
(13)

則在虛擬控制ωc的作用下，式(9)變為

(14)

取快回路滑模面為

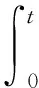
(15)

式中s2=[s21,s22,s23]T；C=diag(c1,c2,c3)，且有ci>0,i=1,2,3；Γ=diag(γ1,γ2,γ3)，且有γi>0,i=1,2,3。

對滑模面(15)求導得

(16)

趨近率取為

(17)

式中K2=diag(k21,k22,k23),k2i>0,i=1,2,3；ε2=diag(ε21,ε22,ε23),ε2i>d2,i=1,2,3。

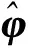
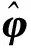
(18)

ωc中含有符號函數項，導致ωc不可導，需用濾波器來獲得近似導數。設濾波方程為

(19)

式中T=diag(T1,T2,T3)為濾波器時間常數矩陣。

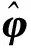
(20)

在控制σ的作用下，式(10)變為

(21)

設式(20)的右端項為U，則有

MRCSσ=U

(22)

由于σ∈R10×1，U∈R3×1，RCS控制要求燃料消耗最少，取性能指標：

(23)

約束條件為

s.t 0≤σi≤1

(24)

可采用線性規劃方法進行優化求解指令σ。

定理1 對于式(4)所示的再入飛行器，采用式(13)作為慢回路虛擬控制量、式(22)的優化結果σ作為快回路控制量，使得姿態控制系統穩定。

證明 慢回路穩定性：設Lyapunov函數：

(25)

對式(25)求導，并將式(14)代入，則有

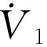
≤-min(k1i)‖e1‖2-min(ε1i-d1)‖e1‖

則慢回路穩定。

快回路穩定性：設Lyapunov函數：

V2=s2Ts2/2

(26)

其對時間的一階導為

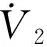
(27)

將式(18)代入式(27)是可得

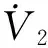
≤-min(k2i)‖s2‖2-min(ε2i-d2)‖s2‖

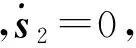
(28)

取Lyapunov函數為

V3=e2Te2/2

(29)

則對其進行求導有

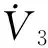
≤-min(ci)‖e2‖2-min(γi)‖e2‖

可見快回路穩定。

為了避免符號函數引起的控制信號高頻顫振，本文采用飽和函數sat(x)代替符號函數sgn(x)。選擇邊界層Δ>0，飽和函數為

(30)

而對于式(20)的控制量σ，不是0-1信號，需采用PWPF調制器進行調制。

2.3 積分補償型PWPF調制器設計

本文在文獻[5-6]中PWPF的基礎上進行了改進，設計了一種積分補償型PWPF調制器(Integral Pulse-Width Pulse-Frequency Modulator, IPWPF)，其原理圖如圖2所示。該PWPF調制器包括前置低通濾波器、施密特觸發器、單位反饋回路和積分補償回路。

圖中，σ為待調制的控制信號，u為0-1式開關信號。記濾波器輸入為e(t)，輸出為

f(t)=f(0)+[kme(t)-f(0)](1-e-t/τm) (31)

記開啟時刻t=0，再次關閉時刻記為t=Ton，則f(0)=d,f(Ton)=d-h，因此滿足

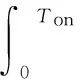
要使IPWPF調制器正常工作，IPWPF調制器的最小信號輸入σmin需滿足

km(kpσmin+kiσminTon)=d

(33)

聯立式(32)及式(33) ，整理可得，最短開啟時間滿足

(34)

可選擇合適的參數組合，用式(34) 來估算最短開啟時間。若推力器開啟最短時間為80ms，則可選取參數組合為：km=1，τm=0.16，d=0.6，h=0.4，kp=2.5，ki=10。

定理2 對于飛行器再入初期的RCS控制，采用圖2所示的IPWPF調制器進行信號的調制，使得RCS調制系統穩定。

證明 對于非線性系統，一般采用描述函數法來分析穩定性。IPWPF調制器等效圖如圖3所示。

將非線性部分的描述函數記為N(A)，并記線性環節為

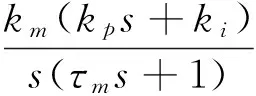
(35)

則閉環系統的特征方程為

1+N(A)G(jω)=0

(36)

其中，非線性環節描述函數為

(37)

作ΓG曲線和-1/N(A)曲線如圖4所示，從圖4中可見，ΓG曲線不包圍-1/N(A)曲線，說明系統穩定。

證畢。

設IPWPF調制器的輸入能量為Qσ，輸出能量為Qu，定義：

(38)

取σ=0.8+0.2sin(πt+0.5)，分別采用IPWPF調制器和傳統PWPF調制器[6]進行調制，IPWPF調制器和傳統PWPF調制器對能量的跟蹤曲線如圖5所示，對比可知，IPWPF調制器的能量跟蹤能力明顯優于傳統PWPF調制器。

3 仿真驗證

飛行器飛行高度為100 km，速度為7500 m/s。控制參數為：K1=diag(0.3,0.8,0.3)，ε1=diag(0.15,0.15,0.1)，C=diag(0.2,0.3,0.2)，Γ=diag(0.02,0.15,0.02)，K2=diag(0.4,1,0.4)，ε2=diag(0.15,0.2,0.1)，T=diag(0.1,0.1,0.1)，Δ=0.2。非線性干擾觀測器參數為：Λ1=diag(0.5,0.2,0.1)，Λ2=(2,2,2)。取期望角度指令為：αc=10°，βc=0°，φVc=5°。采用本文DOB+IPWPF方法和傳統PWPF分別進行仿真分析，其攻角、側滑角和速度傾角跟蹤曲線如圖6～圖8所示。由圖6～圖8知，在傳統PWPF調制方法下，攻角跟蹤穩態誤差為2°，穩態側滑角誤差為1°，傾側角跟蹤穩態誤差為2°。而采用本文DOB+IPWPF方法，攻角跟蹤穩態誤差為0.5°，穩態側滑角誤差為0.5°，傾側角跟蹤穩態誤差為0.5°。由此可見，本文方法控制下，對姿態角跟蹤的穩態性能優于傳統PWPF，擬線性跟蹤的精度比傳統的PWPF高。從動態性能來看，兩種方法的上升時間相當，動態性能相差不大。

圖9為兩種方法消耗的燃料對比圖。由圖9可見，本文RCS控制方法的燃料消耗量比傳統PWPF方法要多。但燃料消耗可通過調節積分補償系數ki來調節。ki越大，精度越高，燃料消耗越多；ki越小，精度越低，燃料消耗越少；合理地選取ki，使得控制既滿足精度要求，又不至于消耗過多的燃料。

4 結論

(1)采用積分補償型脈沖調制器(IPWPF)產生的RCS發動機開關邏輯指令，對輸入信號進行擬線性跟蹤，其跟蹤精度優于傳統的PWPF調制器。

(2)采用滑模變結構控制方法設計控制器，并利用非線性干擾觀測器(DOB)對系統不確定項進行估計，將估計值作為控制系統的補償量，使得控制器具有較強的抗干擾性能，控制精度更高。

[1] 賀成龍, 陳欣, 楊一棟. 一種動態逆解算的RLV混合規劃控制分配研究[J]. 系統工程與電子技術, 2010, 32(9): 1973-1976.

[2] Zhou J, Ji P F, Hu W J. Attitude control algorithm for reusable launch vehicle in reentry flight phase [J]. Journal of China Ordnance, 2009, 5(1): 15-19.

[3] 房元鵬. 可重復使用航天器反作用力控制系統控制方法[J]. 航空學報, 2008, 29(增刊): S97-S101.

[4] David B D, Brian J G, Anhtuan D N. Quantized control allocation of reaction control jets and aerodynamic control surfaces [J]. Journal of Guidance, Control, and Dynamics, 2009, 32(1): 13-24.

[5] Geng J, Sheng Y Z, Liu X D. Finite-time sliding mode attitude control for a reentry vehicle with blended aerodynamic surfaces and a reaction control system [J]. Chinese Journal of Aeronautics, 2014, 27(4): 964-976.

[6] Wang X S, Wang D W, Zhu S Q, et al. Fractional describing function analysis of PWPF modulator[R]. Mathematical Problems in Engineering, 2013, 34(1): 130-137.

[7] Xu Z, Tang S. RLV (Reusable launch vehicle) reentry nonlinear controller design [C]//2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, 2010: 380-383.

[8] 李憲強, 周軍. 再入飛行器多約束姿態控制律設計[J]. 固體火箭技術, 2015, 34(4): 472-476.

[9] James E S, Yuri B S. Launch vehicle attitude control using higher order sliding modes[C]//AIAA Guidance, Navigation, and Control Conference, Toronto, 2010: 1-14.

[10] Sheng Y Z, Geng J, Liu X D, et al. Nonsingular finite-time second order sliding mode attitude control for reentry vehicle[J]. International Journal of Control, Automation, and System, 2015, 13(4): 853-866.

[11] 宋超, 趙國榮, 陳潔. 基于魯棒滑模觀測器的高超聲速飛行器雙環滑模控制[J]. 固體火箭技術, 2012, 35(4): 438-441.

[12] Cui L, Yang Y. Disturbance rejection and robust least-squares control allocation in flight control system [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(6): 1632-1643.

[13] 王芳, 宗群, 田栢苓, 等. 基于魯棒自適應反步的可重復使用飛行器再入姿態控制[J]. 控制與決策, 2014, 29(1): 12-18.

[14] Charles E H, Yuri B S. Sliding mode disturbance observer-based control for a reusable launch vehicle[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1315-1328.

[15] Chen X S, Yang J, Li S H, et al. Disturbance observer based multi-variable control of ball mill grinding circuits [J]. Journal of Process Control, 2009, 19(7):1205-1213.

[16] 黃頔, 郝宇清, 段志生. 可重復使用天地往返飛行器中的多輸入控制問題[J]. 控制理論與應用, 2014,31(7): 878-889.

[17] 及鵬飛, 周軍, 呼衛軍. 可重復使用運載器再入段噴氣選擇邏輯重構研究[J]. 西北工業大學學報, 2007,25(6): 794-799.

[18] 李惠峰．高超聲速飛行器制導與控制技術[M]. 北京：中國宇航出版社，2012.

[19] 劉宇超, 郭建國, 周軍, 等. 基于新型快速Terminal滑模的高超聲速飛行器姿態控制[J]. 航空學報, 2015, 36(7): 2372-2380.

[20] 張天翼, 周軍, 郭建國. 基于干擾觀測器的高速飛行器預測控制律設計[J]. 航空學報, 2014, 35(1): 215-222.

[21] 趙明元, 魏明英, 何秋茹. 基于有限時間穩定和Backstepping 的直接力/氣動力復合控制方法[J]. 宇航學報, 2010, 31(9): 2157-2164.

(編輯：呂耀輝)

Reaction control system design for reentry vehicle

GUO Jian-guo1, ZHANG Tian-bao1, ZHOU Jun1, WANG Guo-qing2

(1.Institute of Precision Guidance and Control, Northwestern Polytechnical University,Xi'an 710072, China；2.China Academy of Launch Vehicle Technology, Beijing 100076, China)

According to the tracking error of reaction control system (RCS), a new precision control strategy is proposed for the initial reentry phase of reentry vehicle. Firstly, a nonlinear disturbance observer (DOB) is used for observing the model uncertainty and/or external disturbances. Secondly, a sliding mode control system for the fast loop and slow loop is designed by back-stepping style, and obtained the optimal combination of RCS by linear optimization. Besides, a Integral PWPF Modulator (IPWPF) is proposed based on traditional PWPF modulator, and its stability is proved by a describing function. Finally, the simulation indicates a great precision of the method.

reentry vehicle；reaction control system；disturbance observer；sliding mode；PWPF modulator

2016-11-18；

2016-12-27。

國家自然科學基金(61473226)；航天創新基金(N14XW0001)。

郭建國(1975—)，男，教授，研究方向為飛行器制導與控制。E-mail:guojianguo@nwpu.edu.cn

V448

A

1006-2793(2017)04-0511-06

10.7673/j.issn.1006-2793.2017.04.020