纖維混編CMC-SiC的殘余熱應力計算①

劉善華，張立同，邱海鵬，殷小瑋，成來飛，劉永勝 ，王 嶺，陳明偉

(1.超高溫復合材料國防科技重點實驗室，西北工業大學，西安 710072；2.中航復合材料有限責任公司 技術發展部，北京 101300)

纖維混編CMC-SiC的殘余熱應力計算①

劉善華1,2，張立同1，邱海鵬2，殷小瑋1，成來飛1，劉永勝1，王 嶺2，陳明偉2

(1.超高溫復合材料國防科技重點實驗室，西北工業大學，西安 710072；2.中航復合材料有限責任公司 技術發展部，北京 101300)

將SiC纖維引入到C/PyC/SiC中，有望減少因C纖維與SiC基體熱膨脹系數不匹配而導致的基體殘余熱應力。研究了C纖維和SiC纖維混編方式和混編比例對復合材料殘余熱應力的影響規律。采用有限元法建模、計算了纖維混編接觸分布和相間分布復合材料的殘余熱應力，結果表明：(1)與C/PyC/SiC比，C纖維和SiC纖維混編增強SiC基復合材料可減少SiC基體的殘余拉應力；(2)相同混編比例時，纖維混編接觸分布((xC-ySiC)/PyC/SiC)復合材料的基體軸向殘余應力比纖維混編相間分布((xC×ySiC)/PyC/SiC)復合材料基體的小；(3)以纖維混編接觸分布為例，SiC基體的軸向殘余應力隨混編復合材料中SiC纖維的增加而減小，但當C纖維和SiC纖維的混編比例由1∶2變為1∶4時，基體的軸向殘余熱應力僅從174 MPa 下降到170 MPa。

SiC 基體；SiC纖維；C 纖維；殘余熱應力；混編

0 引言

連續炭纖維增韌SiC陶瓷基復合材料(C/SiC)因具有耐高溫、高比強、高比模、抗氧化和抗燒蝕等優異性能，且具有類似金屬的斷裂行為、對裂紋不敏感、無災難性損毀等特點，使其具有接替金屬作為新一代高溫結構材料的潛力[1-4]。

C/SiC復合材料的制備溫度一般在1000 °C左右，由于C纖維(Cf)的熱膨脹系數與SiC基體(SiCm)的熱膨脹系數不匹配，當C/SiC復合材料從制備溫度冷卻到室溫時會形成殘余熱應力(Residual thermal stress,RTS)。軸向上，因Cf的熱膨脹系數小于SiCm的熱膨脹系數，C/SiC中SiCm在室溫下受殘余拉應力，而Cf受殘余壓應力。殘余拉應力往往使SiCm存在微裂紋，此外，當復合材料受外在拉應力時，基體所受的殘余拉應力會與復合材料所受的拉應力產生疊加效應，引起SiCm過早開裂，從而使基體失去承載、保護界面和纖維的作用[5]。因此，研究C/SiC復合材料的殘余熱應力分布及如何減少C/SiC復合材料的殘余熱應力至關重要。SiC纖維(SiCf)與SiCm的熱膨脹系數接近[6-7]，將SiCf和Cf混編，從熱膨脹系數匹配的角度看可能會降低由于Cf和SiCm熱膨脹系數不匹配而引起的基體殘余熱應力。

微復合材料(Micro-composites)由單根纖維、界面層和基體組成，是復合材料的基本單元，可用來研究陶瓷基復合材料的殘余熱應力、力學性能和界面性能[8-15]。微復合材料的殘余熱應力分布可在一定程度上反映復合材料的殘余熱應力分布。Mikata等[9]建立了包括纖維、界面和基體的一個徑向尺寸無限大的圓柱模型，對復合材料的殘余熱應力進行研究，該方法從物理學角度研究了纖維和基體之間的相互作用。Bobet等[13-16]推導出一個外徑有限的同軸圓柱體模型，研究了界面類型和界面層厚度對C/SiC復合材料殘余熱應力的影響規律。

盡管不同模型都能對纖維與基體間的殘余熱應力進行計算，但目前對于包含兩種不同纖維混編增韌SiC基復合材料的殘余熱應力計算尚未見報道。本文的主要研究內容包括：(1)C/PyC/SiC殘余熱應力；(2)Cf和SiCf混編方式對復合材料殘余熱應力的影響規律；(3)Cf和SiCf混編比例對復合材料殘余熱應力的影響規律。

1 計算方法

1.1 模型建立

采用版本為4.5a的Comsol軟件建模，并計算復合材料的殘余熱應力。C/SiC和Cf、SiCf混編復合材料的纖維體積分數均為40%，以PyC為界面層，且厚度為0.5 μm，需要說明的是在實際C/SiC復合材料中，PyC界面層的厚度一般為0.07～0.22 μm[17]，但在計算復合材料殘余熱應力時發現，當界面層的厚度低于0.5 μm時，對模型進行網格劃分時容易引起網格奇異，造成計算誤差，而PyC界面層在0.2～0.5 μm之間變化，對復合材料殘余熱應力的變化規律無影響。因此，為方便建模計算，模型中PyC界面層的厚度為0.5 μm。帶箭頭的虛線表示殘余熱應力分析路徑。

C/PyC/SiC微復合材料采用軸對稱模型建模計算，如圖1(a)所示。

Cf和SiCf混編復合材料采用三維模型建模計算，3種復合材料模型的高度均為20 μm。纖維混編方式有兩種：(1)Cf和SiCf在復合材料中相間分布，以(xC×ySiC)/PyC/SiC表示，如圖1(b)所示；(2)Cf和SiCf接觸分布，以(xC-ySiC)/PyC/SiC表示，如圖1(c)所示。其中，x∶y為Cf和SiCf的體積分數比。混編復合材料的應力分析路徑包括連接Cf和SiCf圓心的θ=45°方向和連接SiCf圓心的θ=0°方向，如圖1(b)和1(c)中帶箭頭的虛線所示。

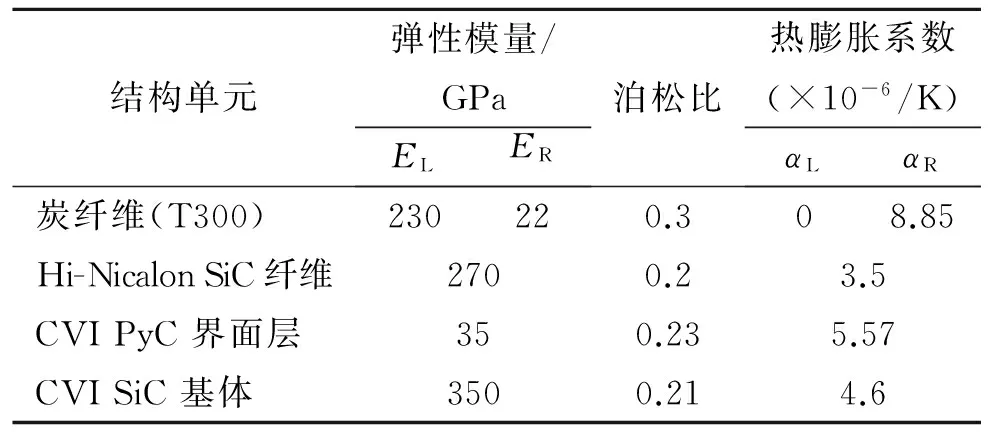
表1 材料體系中結構單元的性能

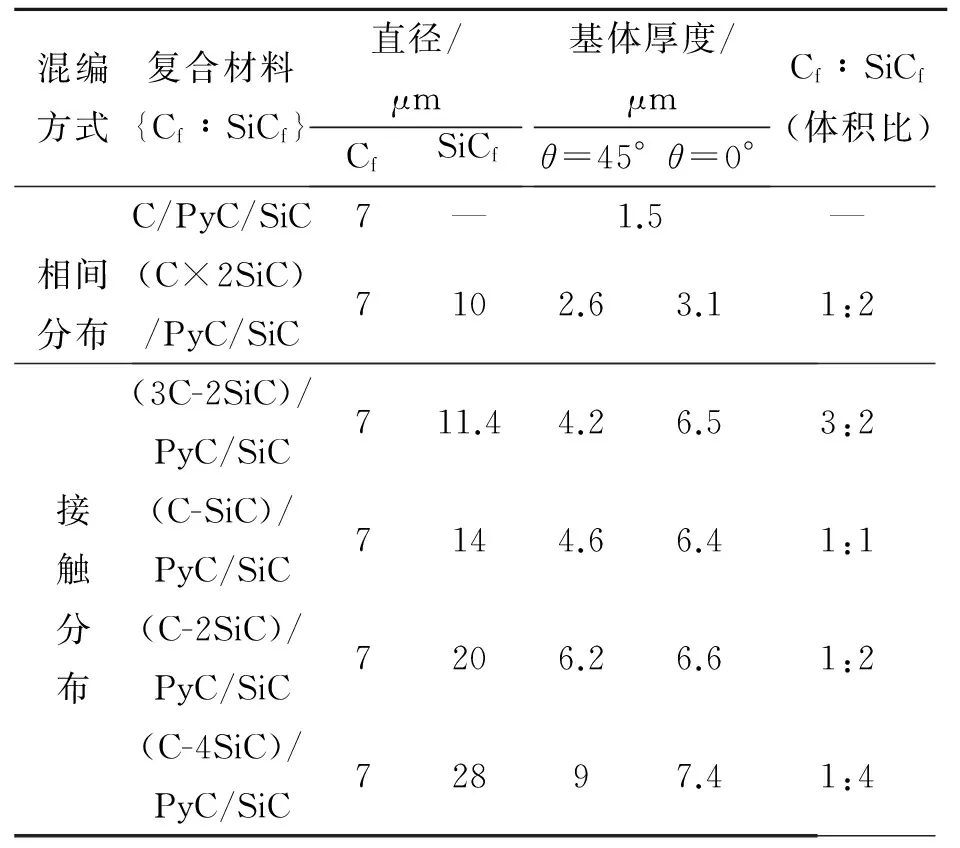
表2 復合材料有限元計算建模尺寸

1.2 模型計算與網格劃分

用于計算的Cf、SiCf、SiCm和PyC界面層的熱物理性能參數列于表1[16,18-21]。復合材料的殘余熱應力的計算溫度差為1000 ℃。C/PyC/SiC、不同混編方式和不同混編比例復合材料的模型尺寸列于表2。其中，Cf和SiCf不同混編比例復合材料的模型是通過改變SiCf直徑(Cf直徑不變)建立的。對圖1的3個模型進行網格劃分后的參數列于表3。

邊界條件為兩端自由，為保證幾何單元的對稱性，所有網格節點在對稱面上都被約束為法向位移相同。下標 L和R 代表軸向和徑向方向。

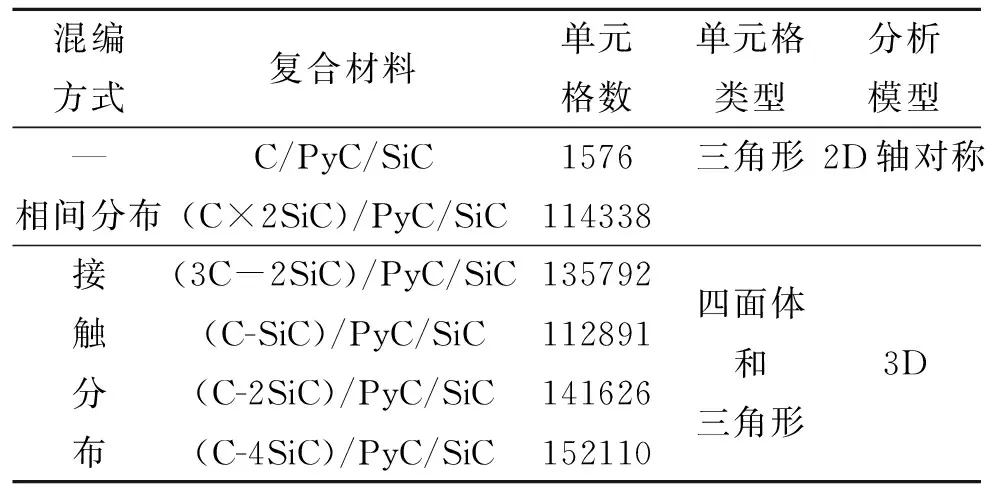
表3 有限元計算模型網格參數

2 結果與討論

2.1 C/PyC/SiC的殘余熱應力

圖2為C/PyC/SiC復合材料的殘余熱應力分布圖。因各結構單元的應力沿徑向呈梯度分布，故將各結構單元所受殘余熱應力的平均值標于圖2中。由圖可2見：(1)軸向上，Cf的殘余壓應力為-880 MPa，PyC的殘余拉應力為134 MPa，SiCm的殘余拉應力為726 MPa。(2)徑向上，C/PyC/SiC各結構單元均受殘余拉應力。其中，Cf、PyC和SiCm的殘余拉應力分別為280、251、100 MPa。

2.2 混編方式對復合材料殘余熱應力分布的影響

2.2.1 混編相間分布復合材料的殘余熱應力分布

圖3是Cf和SiCf混編比例為1∶2時，(C×2SiC)/PyC/SiC在θ=45°方向的軸向和徑向殘余熱應力。由圖3可見：(1)軸向應力如圖3(a)所示，Cf和SiCf受殘余壓應力，PyCon Cf、PyCon siCf和SiCm受殘余拉應力。沿45°方向，Cf的壓應力逐漸增加，SiCf的壓應力基本不變，SiCm的拉應力逐漸降低。PyCon Cf的拉應力大于PyCon siCf的拉應力。(2)徑向應力如圖3(b)所示，Cf、PyCon Cf、PyCon siCf和SiCm受殘余拉應力，SiCf部分受拉應力，部分受壓應力。沿45°方向，Cf和SiCm的拉應力逐漸降低，SiCf由受拉應力變為受壓應力。PyCon Cf的拉應力大于PyCon siCf的拉應力。

圖4是(C×2SiC)/PyC/SiC在θ=0°方向的軸向和徑向殘余熱應力分布圖。從圖4可看出:(1)軸向應力見圖4(a)，SiCm、PyCon siCf受殘余拉應力，SiCf受殘余壓應力。沿0°方向，SiCm的拉應力不斷增大，SiCf的壓應力基本不變。(2)徑向應力見圖4(b)，SiCm、PyCon siCf和SiCf均受殘余壓應力且沿0°方向各結構單元的殘余壓應力逐漸增大。

2.2.2 混編接觸分布復合材料的殘余熱應力分布

圖5是Cf和SiCf混編比例為1∶2時，(C-2SiC)/PyC/SiC在θ=45°方向的軸向和徑向殘余熱應力。由圖5可見:(1)軸向應力如圖5(a)所示，SiCm、PyCon Cf、PyCon siCf和SiCf受殘余拉應力，Cf受殘余壓應力。沿45°方向，SiCm的殘余拉應力不斷增加，Cf的壓應力不斷降低。PyCon Cf的拉應力小于PyCon siCf的拉應力。(2)徑向應力如圖5(b)所示，SiCm、PyCon Cf、PyCon siCf和Cf均受殘余拉應力，SiCf部分受拉應力、部分受壓應力。沿45°方向，SiCm的拉應力不斷增加，Cf的拉應力先增后減，SiCf由受拉應力變為受壓應力。PyCon Cf的拉應力大于PyCon siCf的拉應力。

圖6是(C-2SiC)/PyC/SiC在θ=0°方向的軸向和徑向殘余熱應力分布圖。由圖6可見：(1)軸向應力如圖6(a)所示，SiCm和PyCon siCf受殘余拉應力，SiCf部分受壓應力、部分受拉應力。沿0°方向，SiCf由受殘余拉應力變為受殘余壓應力。(2)徑向應力如圖6(b)所示，SiCm、PyCon siCf和SiCf均受殘余壓應力。沿0°方向，SiCm和PyCon siCf的壓應力逐漸增大，SiCf的壓應力先增加后減小。

觀察圖3～圖6，(C×2SiC)/PyC/SiC和(C-2SiC)/PyC/SiC中結構單元的殘余應力分布均存在一定應力梯度。結構單元間的距離越近，熱失配作用越明顯，其殘余應力值也越大。由于Cf和SiCf在兩種混編復合材料中的分布不同，為研究混編和混編方式對復合材料結構單元殘余熱應力的影響規律，需對C/PyC/SiC和兩種纖維混編復合材料中各結構單元殘余熱應力取平均值后對比研究。

2.2.3 混編方式對復合材料殘余熱應力分布的影響

表4 為C/PyC/SiC、(C×2SiC)/PyC/SiC和(C-2SiC)/PyC/SiC復合材料結構單元在θ=45°和0°方向的軸向和徑向殘余熱應力對比。

軸向上，由表4可見：(1)兩種混編復合材料中SiCm在θ=45°和0°方向的殘余拉應力均低于其在C/PyC/SiC中的殘余拉應力，且(C-2SiC)/PyC/SiC中SiCm在兩個方向的拉應力均低于(C×2SiC)/PyC/SiC中SiCm的拉應力。(2)Cf和PyCon Cf的軸向應力在θ=45°方向，與C/PyC/SiC相比，(C×2SiC)/PyC/SiC中Cf的壓應力減小，PyCon Cf的拉應力增大；(C-2SiC)/PyC/SiC中Cf的壓應力增大，PyCon Cf的拉應力減小。(3)SiCf和PyCon siCf的軸向應力在θ=45°和0°方向，SiCf在(C×2SiC)/PyC/SiC中受殘余壓應力，而在(C-2SiC)/PyC/SiC中受殘余拉應力。PyCon siCf在兩種混編復合材料中均受殘余拉應力，且(C×2SiC)/PyC/SiC中PyCon siCf在兩個方向的拉應力均大于(C-2SiC)/PyC/SiC中PyCon siCf的拉應力。

表4 有限元法計算C/PyC/SiC、(C×2SiC)/PyC/SiC和(C-2SiC)/PyC/SiC復合材料各結構單元在θ=45°和0°方向軸向和徑向的殘余熱應力

以上結果表明，與C/PyC/SiC相比，Cf和SiCf混編(均以混編比例為1∶2為例)可減小SiCm的軸向殘余拉應力，但兩種混編方式對復合材料結構單元的殘余熱應力影響又有所不同：

(1)在(C×2SiC)/PyC/SiC中，Cf和SiCf相間分布在SiCm中，Cf和SiCf不接觸。在θ=45°方向，可近似看成是一個C/PyC/SiC和一個SiC/PyC/SiC微復合材料并在一起。SiCm殘余拉應力的降低主要是由于其與Cf間的殘余應力較大，而與SiCf間的殘余應力較小，造成SiCm的應力梯度分布，取平均值后SiCm的殘余拉應力低于C/PyC/SiC中SiCm的殘余拉應力，根據作用力與反作用力原理，Cf的殘余壓應力比C/PyC/SiC的低。

(2)在(C-2SiC)/PyC/SiC中，Cf與SiCm和SiCf均接觸，由于Cf軸向熱膨脹系數最小，故SiCm和SiCf均受殘余拉應力。θ=45°方向上，SiCf的存在使部分原本SiCm所受的殘余拉應力轉移到SiCf上，故SiCm的拉應力值最小，而Cf因受SiCm和SiCf的殘余壓應力的疊加作用，其殘余壓應力值最大。在θ=0°方向上，Cf與SiCf仍相互作用，使得SiCf受拉應力，但由于在該方向上SiCm對SiCf產生壓應力，取平均值后，SiCf受約1 MPa的殘余拉應力。

徑向上，由表4看見，(1)SiCm的徑向應力在θ=45°方向，與C/PyC/SiC相比，(C×2SiC)/PyC/SiC和(C-2SiC)/PyC/SiC中SiCm的殘余拉應力均增大，且前者的殘余拉應力小于后者的。(2)(C×2SiC)/PyC/SiC和(C-2SiC)/PyC/SiC中Cf和PyCon Cf的殘余拉應力在θ=45°方向與C/PyC/SiC相比均減小，且前者的殘余拉應力略小于后者的。(3)SiCf和PyCon siCf的徑向應力的變化趨勢不同。在θ=45°和0°方向，SiCf在(C×2SiC)/PyC/SiC中均受殘余壓應力；在θ=45°方向，SiCf在(C-2SiC)/PyC/SiC中受殘余拉應力，而在θ=0°方向，SiCf受殘余壓應力，且壓應力值小于其在(C×2SiC)/PyC/SiC的壓應力。在θ=45°，PyCon siCf在(C×2SiC)/PyC/SiC和(C-2SiC)/PyC/SiC中均受殘余拉應力，且前者的拉應力小于后者；而在θ=0°方向，其PyCon siCf均受殘余壓應力，且后者的壓應力略大于前者。上述結果的原因在于：(1)在(C×2SiC)/PyC/SiC中，由于Cf和SiCf不接觸。在θ=45°方向，SiCm受Cf的徑向拉應力。在θ=0°方向，(C×2SiC)/PyC/SiC中SiCf受SiCm的殘余壓應力。(2)在(C-2SiC)/PyC/SiC中，Cf與SiCf和SiCm接觸，在θ=45°方向，Cf對SiCf和SiCm同時產生殘余拉應力，與C/PyC/SiC相比，SiCm的拉應力增大，且其值大于(C×2SiC)/PyC/SiC中SiCm的拉應力。在θ=0°方向，Cf對SiCf仍有作用，一方面SiCm對SiCf產生壓應力，另一方面Cf對SiCf產生拉應力，兩種應力中和后，SiCm和SiCf均受殘余壓應力，且其壓應力均比(C×2SiC)/PyC/SiC中SiCm和SiCf的小。

綜上所述，(C-2SiC)/PyC/SiC中SiCm的軸向殘余拉應力比(C×2SiC)/PyC/SiC的小，表明復合材料的基體裂紋也較少，SiCm的斷裂能高，從而提高復合材料的基體開裂應力。因此，從軸向殘余熱應力的變化看，選擇Cf和SiCf混編接觸分布方式為宜。從徑向殘余熱應力變化看，(C×2SiC)/PyC/SiC中SiCm的在θ=45°方向的拉應力低于(C-2SiC)/PyC/SiC中SiCm的拉應力，且(C×2SiC)/PyC/SiC中SiCm在θ=0°方向的壓應力高于(C-2SiC)/PyC/SiC中SiCm的壓應力。根據庫倫摩擦定律，當基體受壓(或受拉相對小)時，其界面剪切強度將會增加，有利于提高復合材料的基體開裂應力[22-23]。因此，從徑向殘余熱應力的變化看，選擇纖維混編相間分布為宜。

3 纖維混編比例對復合材料結構單元殘余熱應力的影響

由于纖維混編接觸分布對SiCm的軸向殘余熱應力的影響較為顯著，故選擇該混編方式研究纖維混編比例對復合材料結構單元殘余熱應力的影響規律。圖7為Cf與SiCf接觸分布時不同混編比例[(xC-ySiC)/PyC/SiC，x：y=3∶2、1∶1、1∶2和1∶4]復合材料結構單元的殘余熱應力變化圖。

隨混編復合材料中SiCf體積分數的增加，可看出:

(1)在θ=45°方向，軸向應力如圖7(a)所示，SiCm、PyCon siCf、SiCf和PyCon Cf的拉應力逐漸下降，而Cf的壓應力逐漸增加；徑向應力如圖7(b)所示，Cf、PyCon Cf和PyCon siCf的拉應力逐漸增加，SiCm和SiCf的拉應力逐漸減小。

(2)在θ=0°方向，軸向應力如圖7(c)所示，SiCm、SiCf和PyCon siCf的拉應力逐漸下降，當Cf和SiCf混編比例由1∶2變為1∶4時，SiCf、和PyCon siCf由受拉應力變為受壓應力；徑向應力如圖7(d)所示，SiCm、SiCf和PyCon siCf的壓應力逐漸減小。

(3)當Cf和SiCf混編比例由1∶2增至1∶4時，上述結構單元的軸向和徑向應力的變化趨勢(增加或減小)減緩，尤其是SiCm的軸向拉應力僅從174 MPa減少至170 MPa。

4 結論

(1)C/PyC/SiC各結構單元的的殘余熱應力計算結果表明，軸向上，Cf受殘余壓應力，PyCon Cf和SiCm受殘余拉應力，其應力值分別為-880、134、726 MPa。徑向上，上述3種結構單元均受殘余拉應力，其應力值分別為280、251、100 MPa。

(2)Cf和SiCf混編比例等于1∶2時，纖維混編相間分布和接觸分布復合材料結構單元的殘余熱應力與C/PyC/SiC的相比，軸向上，(C×2SiC)/PyC/SiC和(C-2SiC)/PyC/SiC中SiCm的拉應力從726 MPa分別減少至(349、227 MPa，θ=45°；174、39 MPa，θ=0°)；Cf的壓應力從-880 MPa分別減小和增大至(-773、-1073 MPa)，從軸向殘余熱應力的變化看，選擇Cf和SiCf混編接觸分布為宜。徑向上，(C×2SiC)/PyC/SiC和 (C-2SiC)/PyC/SiC 中SiCm在θ=45°方向從100 MPa的拉應力分別增大至123、145 MPa，而在θ=0°方向，則分別變為-43和-28 MPa的壓應力，從徑向殘余熱應力變化看，選擇Cf、SiCf相間分布為宜。

(3)以纖維混編接觸分布方式為例，隨SiCf體積分數的增加，軸向上，SiCm、SiCf、PyCon siCf和PyCon Cf的拉應力逐漸減小，Cf的壓應力逐漸增大。徑向上，在θ=45°方向，Cf、PyCon Cf、PyCon siCf的拉應力逐漸增大，而SiCm和SiCf的拉應力逐漸減小；在θ=0°方向，SiCm、SiCf和PyCon siCf的壓應力逐漸減小。當Cf和SiCf混編比例由1∶2增變為1∶4時，復合材料結構單元的軸向和徑向殘余熱應力的變化趨勢(增大或減小)減緩，尤其是SiCm的軸向拉應力在θ=45°方向僅從174 MPa減小至170 MPa。

[1] Naslain R.Design,preparation and properties of non-oxide CMCs for application in engines and nuclear reactors: an overview[J].Composites Science and Technology,2004,64(2): 155-170.

[2] Naslain R.SiC-matrix composites: Non-brittle ceramics for thermostructural application[J].International Journal of Applied Ceramic Technology,2005,2(2): 75-84.

[3] 張立同.纖維增韌碳化硅陶瓷基復合材料-模擬、表征與設計[M].北京: 化學工業出版社,2009: 1-45.

[4] 張立同,成來飛.連續纖維增韌陶瓷基復合材與可持續發展戰略探討[J].復合材料學報,2007,24(2): 1-6.

[5] Liu Shan-hua,Zhang Li-tong,Yin Xiao-wei,et al.Proportional limit stress and residual thermal stress of 3D SiC/SiC composite[J].Journal of Materials Science & Technology,2014,30(10): 959-964.

[6] Luan Xin-gang,Cheng Lai-fei,Xie Cong-wei.Stressed oxidation life predication of 3D C/SiC composites in a combustion wind tunnel [J].Composites Science and Technology,2013,88: 178-183.

[7] Takeda M,Sakamoto J,Imai Y,et al.Thermal stability of the low-oxygen-content silicon carbide fiber,Hi-Nicalon TM[J].Composites Science and Technology,1999,59: 813-819.

[8] Iesan D.Thermal stresses in composite cylinders[J].Journal of Thermal Stresses,1980,3(4): 495-508.

[9] Mikata Y,Taya M.Stress field in a coated continuous fiber composite subjected to thermo-mechanical loadings[J].Journal of Composite Materials,1985,19 (6): 554-578.

[10] Warwick C M,Clyne T W.Development of composite coaxial cylinder stress analysis model and its application to SiC monofilament systems[J].Journal of Materials Science,1991,26(14): 3817-3827.

[11] Lamon J,Lissart N,Rechiniac C,et al.Micromechanical and statistical approach to the behavior of CMC's.ceramic-engineering-and-science-proceedings[M].New York: John Wiley & Sons,Inc.1993,14(9-10): 1115-1124.

[12] Lamon J,Rebillat F,Evans A G.Microcomposite test procedure for evaluating the interface properties of ceramic matrix composites[J].Journal of the American Ceramic Society,1995,78(2): 401-405.

[13] Bobet J,Sur l`emploi de MoSi2comme interphase dans les matériaux composites à matrice SiC élaborés par CVD/CVI[D].Annexe no 2,Thèse no 987,Bordeaux.1993.

[14] Mori T,Tanaka K.Average stress in matrix and average elastic energy of materials with misfitting inclusions[J].Acta Metallurgica,1973,21(5): 571-574.

[15] Naito N,Hsueh C H.Residual stress and strain in pyrolytic boron nitride resulting from thermal anisotropy[J].Journal of Materials Science,1988,23(6): 1901-1905.

[16] Bobet J.L,Lamon J.Thermal residual stresses in ceramic matrix composites-I.Axisymmetrical model and finite element analysis[J].Acta Metallurgica et Materialia,1995,43(6): 2241-2253.

[17] 董寧.碳化硅陶瓷基復合材料的熱解炭界面相優化研究[D].西安: 西北工業大學,2007: 42.

[18] Mei H.Measurement and calculation of thermal residual stress in fiber reinforced ceramic matrix composites[J].Composites Science and Technology,2008,68(15-16): 3285-3292.

[19] Wongsawaeng D.Modeling failure mechanism of designed-to-fail particle fuel[J].Nuclear Engineering and Technology,2009,41(5): 715-722.

[20] Honjo K.Fracture toughness of PAN-based carbon fibers estimated from strength-mirror size relation[J].Carbon,2003,41(5): 979-984.

[21] ?ünal,Bansal N P.In-plane and interlaminar shear strength of a unidirectional Hi-Nicalon fiber-reinforced celsian matrix composite[J].Ceramics International,2002,28(5): 527-540.

[22] Evans A G,Zok F W.The physics and mechanics of fibre-reinforced brittle matrix composites[J].Journal of Materials Science,1994,29(15): 3857-3896.

[23] Singh R N.Influence of interfacial shear stress on first-matrix cracking stress in ceramic-matrix composites[J].Journal of the American Ceramic Society,1990,73(10): 2930-2937.

(編輯：薛永利)

Calculation on residual thermal stress for hybrid fiber reinforced CMC-SiC

LIU Shan-hua1,2,ZHANG Li-tong1, QIU Hai-peng2, YIN Xiao-wei1, CHENG Lai-fei1, LIU Yong-sheng1, WANG Ling2,CHEN Ming-wei2

(1.Science and Technology on Thermo-structural Composite Materials Laboratory,Northwestern Polytechnical University, Xi'an 710072,China;2.ACIV Composite Corporation LTD, Technical Development Department,Beijing 101300)

It was anticipated that the residual thermal stress in C/PyC/SiC composite,which was due to the coefficients of thermal expansion mismatch between carbon fiber and SiC matrix,would be decreased by introducing the silicon carbide fiber to the composites.The effects of hybrid styles and hybrid ratio between the carbon fiber and silicon carbide fiber on the residual thermal stress in the composites were studied by constructing the finite element models and calculation.The results show that:(1) the residual thermal stresses in carbon fiber and silicon carbide fiber hybrid reinforced SiC matrix composites are lower than those in C/PyC/SiC composites;(2) the axial residual thermal stresses of SiC matrix in hybrid composites with contacted distribution of carbon fiber and silicon carbide fiber ((xC-ySiC)/PyC/SiC) are lower than those in hybrid composites with alternative distribution of carbon fiber and silicon carbide fiber ((xC×ySiC)/PyC/SiC) at the same ratio of carbon fiber to silicon carbide fiber.(3) Taking an example of contacted distribution of carbon fiber and silicon carbide fiber in ((xC-ySiC)/PyC/SiC) composites,the axial residual thermal stresses of SiC matrix are reduced with the silicon carbide fiber volume percent increases in the ((xC-ySiC)/PyC/SiC) composites.However,the axial residual thermal stresses in SiC matrix decreases from 174 MPa to 170 MPa only when the hybrid fiber volume percent ratio of carbon fiber to silicon carbide fiber change from 1∶2 to 1∶4.

SiC matrix;SiC;carbon fiber;residual thermal stress; hybrid

2016-10-14；

2016-11-07。

自然科學基金(51372204)。

劉善華(1984—),男,博士,研究方向為陶瓷基復合材料。E-mail：shanhualiu@yahoo.com

V258

A

1006-2793(2017)04-0493-08

10.7673/j.issn.1006-2793.2017.04.017