基于串級模糊自適應PID的起重機防搖控制研究

劉 斌，諶海云

（西南石油大學 電氣信息學院，成都 610500）

基于串級模糊自適應PID的起重機防搖控制研究

劉 斌1，諶海云1

（西南石油大學 電氣信息學院，成都 610500）

以橋式起重機的吊重系統為研究對象，利用拉格朗日方程建立吊重系統的狀態空間模型，在Matlab/Simulink中建立控制小車位移和吊重擺角的串級PID防搖控制仿真模型，在內環引入模糊自適應PID控制對串級PID控制模型進行改進。仿真結果顯示引入模糊自適應PID控制后，防搖控制系統的控制效果更好，尤其對擺角的控制，超調減小，調節時間加快。最后，利用貝加萊的防搖控制系統實驗平臺對模糊自適應PID防搖控制系統進行驗證。

橋式起重機；Matlab/Simulink；串級PID；模糊自適應PID；貝加萊

0 引言

橋式起重機是港口運輸、裝備制造等行業重要的裝載工具，但在運行過程中小車的加、減速以及風力等外界干擾的影響都會導致吊重貨物的擺動。文獻[1]綜述了防搖控制系統的發展，并介紹人工防搖、機械防搖和電子防搖三種常用的防搖方法。文獻[2]中對橋式起重機吊擺系統和變頻調速系統進行數學建模，并通過Matlab仿真驗證模型的精確性。文獻[3]建立以位移和位移變化率為輸入的位移模糊控制器，以擺角和擺角變化率為輸入的擺角模糊控制器，通過仿真驗證雙模糊控制器對系統的防搖效果。文獻[4]對集裝箱起重機的吊擺設備進行仿真分析，并設計基于富士PLC的防搖控制系統用于實際吊裝現場中，運行效果良好。

本文基于拉格朗日方程建立起橋式起重機的狀態空間模型，在Matlab/Simulink中搭建控制位移和擺角的串級PID控制模型，然后，在串級PID控制的基礎上將模糊自適應PID控制引入內環代替原來單純的PID控制，通過仿真實驗對比兩種控制方式的控制效果。最后，在貝加萊防搖控制系統平臺上對串級模糊自適應PID控制系統進行實驗測試，以驗證理論分析的結果。

1 起重機防搖系統的數學模型

實際的橋式起重機模型很復雜，為了理論分析的方便，此處對系統模型作簡化處理，假設如下：

1）鋼絲繩（吊繩）的質量和長度變化忽略不計；

2）風力、空氣阻力以及鋼絲繩與小車連接處的摩擦力忽略不計；

3）系統的彈性形變忽略不計；

4）將吊起的貨物視為無體積的質點。

得到起重機的簡化模型如圖1所示。

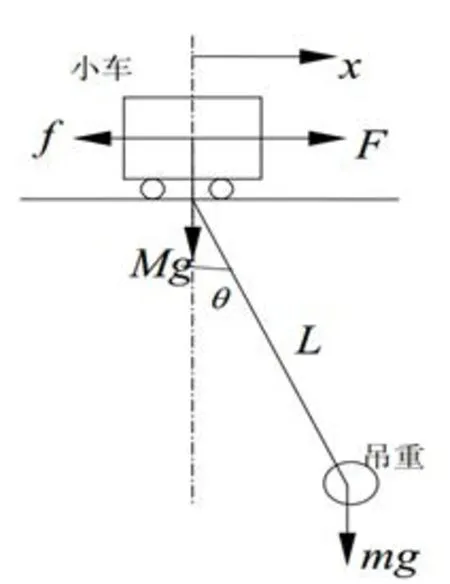
圖1 小車、吊重力學簡化模型

設小車質量為M（質量單位為kg），吊重質量為m，小車與軌道間的摩擦系數為，鋼絲繩長度為L，小車水平驅動力為F，吊重擺角（鋼絲繩與垂直方向的夾角）為

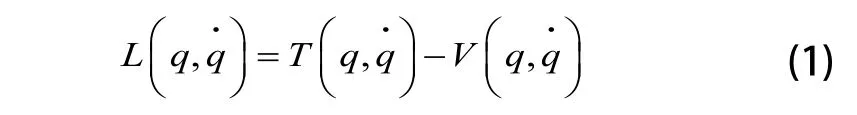
拉格朗日（Lagrange）方程為：

其中，L為拉格朗日算子，T為系統的動能函數，V為系統的勢能函數，q,為拉格朗日變量，分別為廣義坐標和廣義速度。由圖2.1可知，以小車質心為坐標原點，設小車和吊重的坐標分別為：

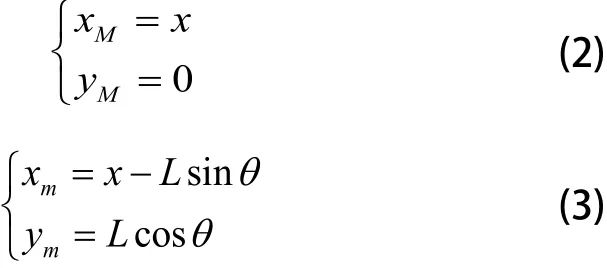
計算得到系統的動能為：

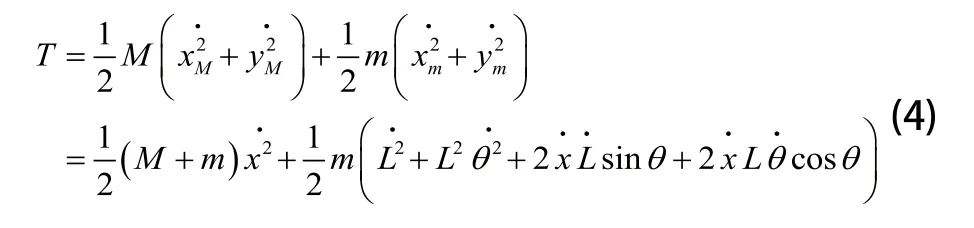
勢能為：

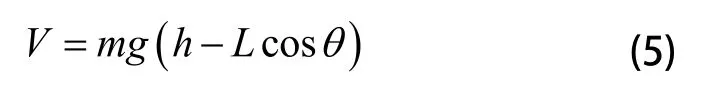
則系統的拉格朗日算子為：

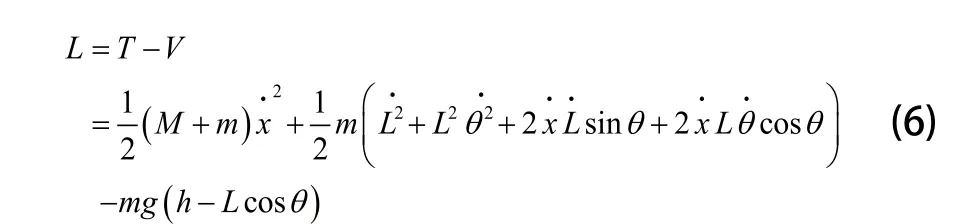
再根據拉格朗日方程建立起橋式起重機的動力學微分方程：

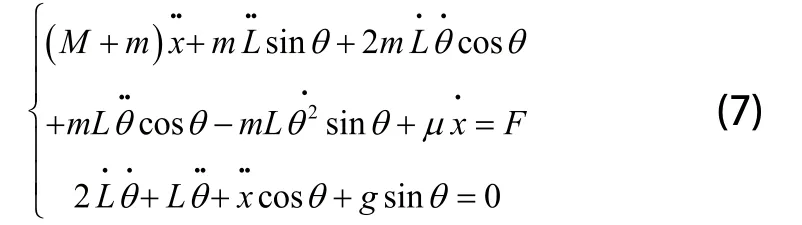
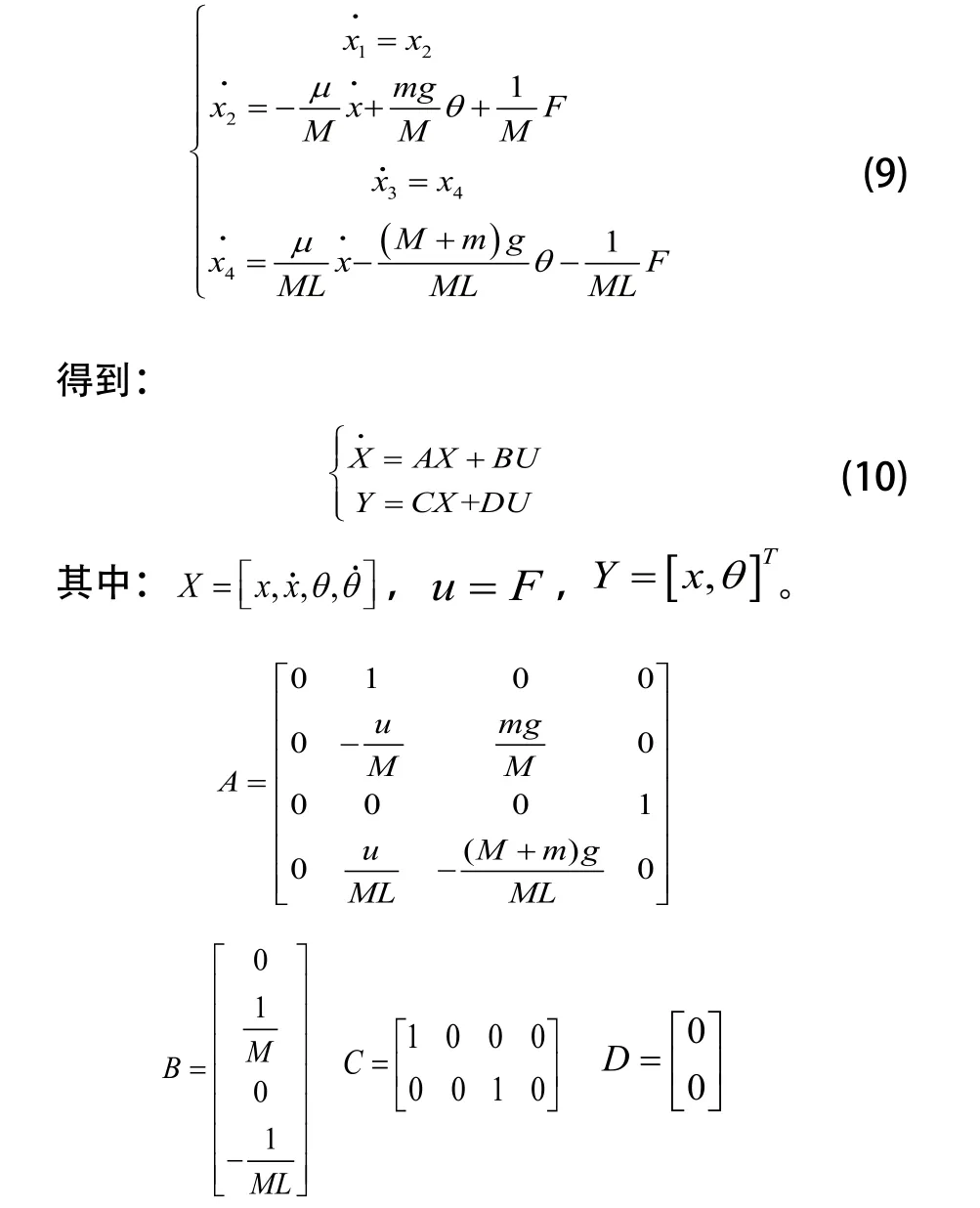
3 仿真研究

3.1 串級PID控制

利用前文中已經建立的橋式起重機的狀態空間模型，在Matlab/Simulink中搭建起控制位置和擺角的串級PID防搖控制仿真模型如圖3.1所示。

該控制模型的內環是對擺角進行控制，目的是控制擺角 在0°左右，讓吊重盡量在垂直方向上不晃動；外環是對小車位移的控制，控制小車準確地停靠在設定的位置。仿真結果如圖3.2、3.3所示。

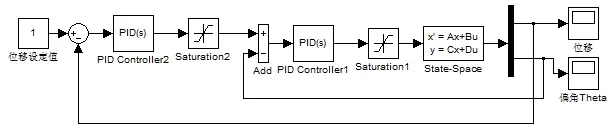
圖2 串級PID控制

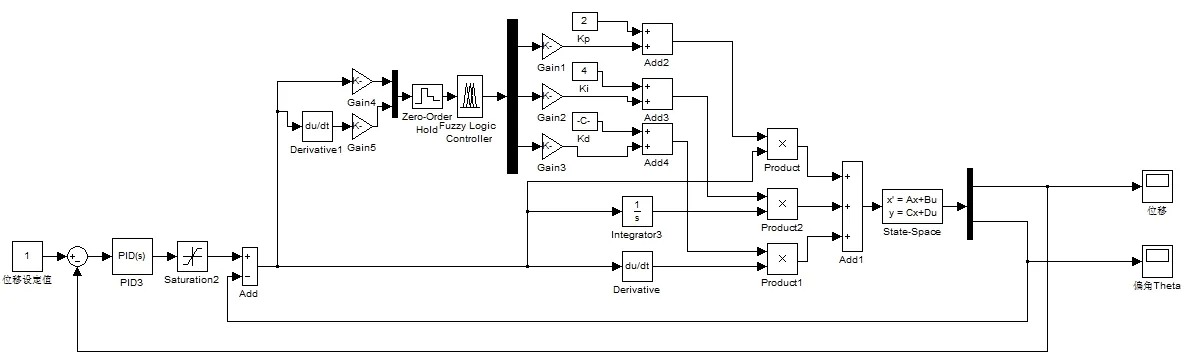
圖3 模糊自適應PID控制

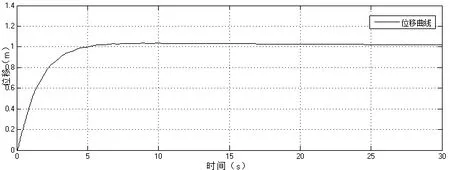
圖4 位移曲線

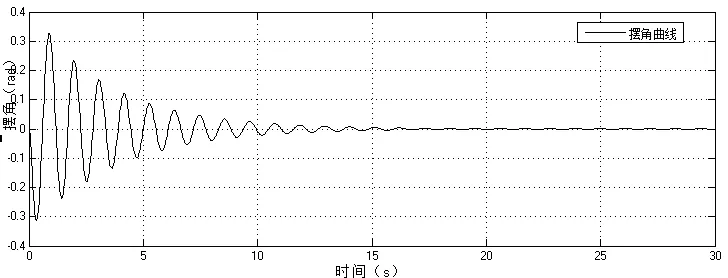
圖5 擺角曲線

從以上圖中可以看出，串級PID對位移的控制已經能達到較好的效果，但對擺角的控制并不理想，擺角的調節時間在t=18s左右，調節過程較長，擺角波動較大，不利于在實際生產中的應用。

3.2 串級模糊自適應PID控制

串級PID控制對擺角的控制不夠理想，主要因為在運行過程中擺角受到小車速度、軌道間的摩擦力、風力等外界因素的干擾。模糊自適應PID控制是將PID控制與模糊控制兩種控制方法相結合，發揮PID控制精度高和模糊控制靈活、適應性強的特點。

3.2.1 控制策略設計

針對串級PID控制的內環PID控制器主要是對擺角的控制，控制效果不甚理想。故提出將模糊控制算法引入內環的想法，控制策略為以進入內環的偏差信號e和偏差變化信號ec作為模糊控制器的輸入變量，PID控制器的三個增量參數?kp，?ki，?kd作為模糊控制器的輸出變量。采用模糊推理的思想對PID控制器的三個參數進行在線整定，以使控制效果達到最優，建立仿真模型如圖3.4所示。

建立Matlab仿真時，模糊控制器的輸入輸出變量均采用“負大”（NB），“負中”（NM），“負小”（NS），“零”（ZO），“正小”（PS），“正中”（PM），“正大”（PB）7個模糊集來表征，隸屬函數都為三角形形式。如圖3.5—3.10為各輸入輸出變量的隸屬函數曲線。

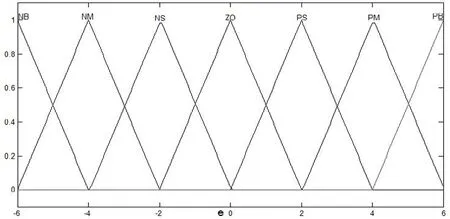
圖6 輸入偏差e的隸屬函數曲線

圖7 輸入偏差變化率ec的隸屬函數曲線

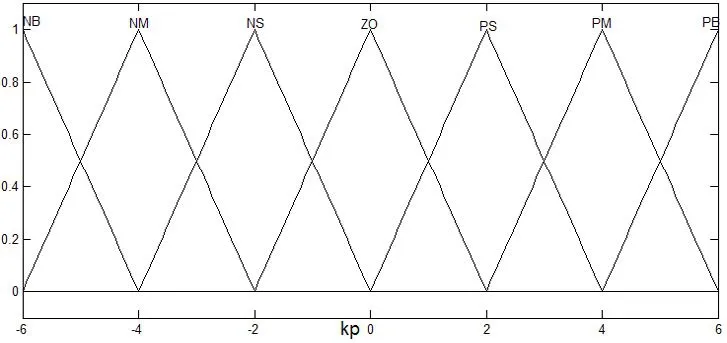
圖8 輸出?kp的隸屬函數曲線

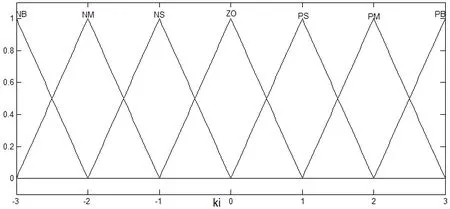
圖9 輸出?ki的隸屬函數曲線

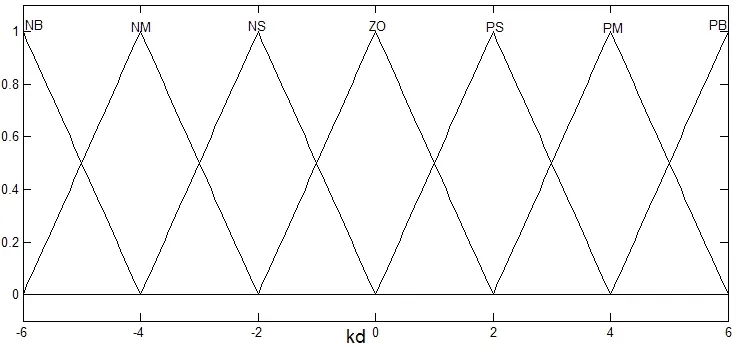
圖10 輸出?kd的隸屬函數曲線

3.2.2 模糊控制規則

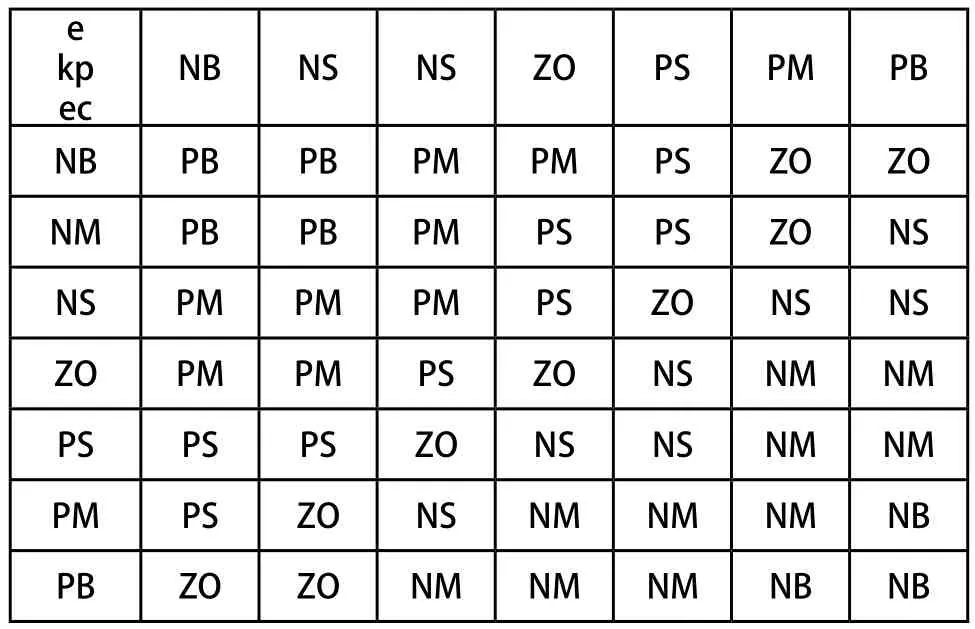
表1 比例增量參數 的控制規則

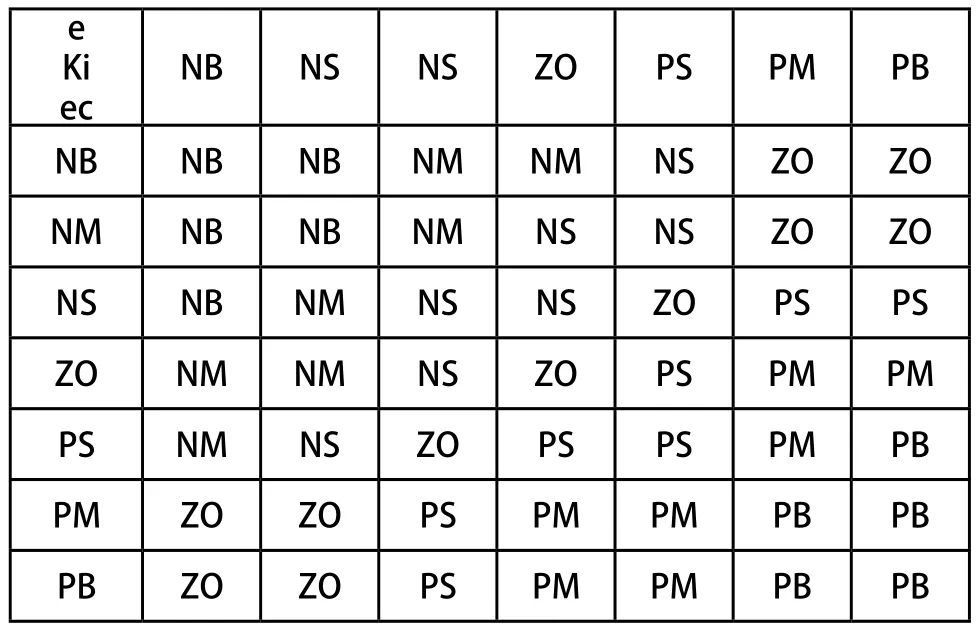
表2 積分增量參數?ki的控制規則

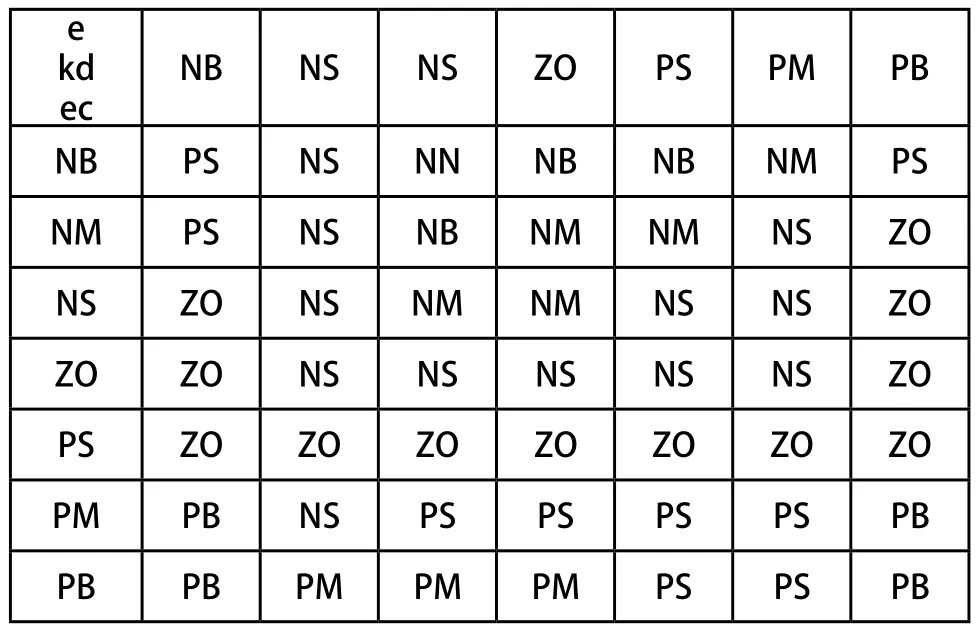
表3 微分增量參數?kd的控制規則

3.2.3 仿真分析

在串級PID控制的基礎上，內環引入模糊控制算法，通過?kp，?ki和?kd三個增量參數分別對內環PID的比例、積分、微分參數進行自動的調節，實現PID參數的在線整定。對比仿真結果如圖3.10、3.11所示。

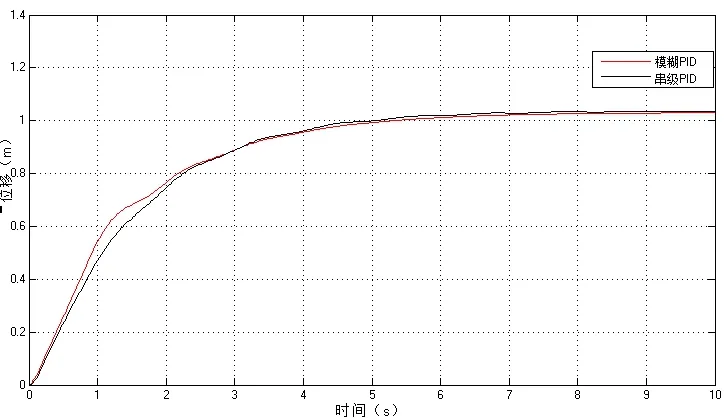
圖11 位移曲線對比

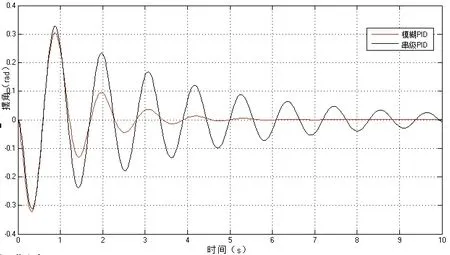
圖12 擺角曲線對比

從圖中可以看出，內環替換為模糊自適應PID控制后，對位移的控制沒有太大的改變，但是對擺角的控制改善卻明顯，模糊自適應PID控制下擺角的波動明顯減小，調節時間t=5s速度加快，擺角能夠較快地穩定在0°左右。可見，改進后的串級模糊自適應PID的控制效果優于傳統的串級PID的控制效果。

4 實驗驗證

前面已經從仿真研究上得出串級模糊自適應PID控制策略對小車速度和吊重擺角具有較好的控制效果，防搖效果明顯，能夠提高起重機的工作效率。為驗證該控制算法在實際的工作中是否具有較優的防搖作用，本設計利用貝加萊的防搖控制系統實驗平臺進行了防搖控制實驗。該實驗平臺主要由X20 PLC 及IO 模塊，ACOPOSmicro 伺服驅動器，8LV 伺服電機及配套的電源模塊等組成。防搖系統裝置包括同步帶直線導軌、負載小車和擺錘。實物如圖4.1所示。

圖13 貝加萊防搖控制平臺

實驗平臺以X20PLC作為控制器，設計控制框圖如圖4.2所示。

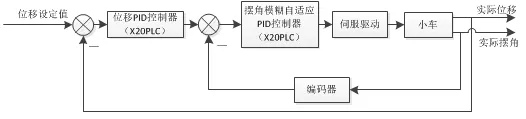
圖14 控制系統框

在Matlab/Simulink中已安裝的B&R Automation Studio Toolbox工具箱，將Simulink的仿真程序轉換為C語言導入X20PLC直接運行，如圖4.3所示。利用AS中的Trace套件記錄擺角和位移的曲線，試驗中考慮到實驗平臺的實際情況對參數和設定值都作出相應的調整，其中位移設定值s=40cm，通過實驗得到一組擺角和位移的曲線如圖4.4所示。

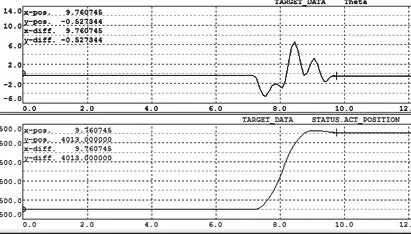
圖16 實驗曲線

分析實驗曲線擺角最大在°以內，調節時間在2.5s左右，位移誤差0.13cm。雖然與理論分析的結果有一定的出入，但是可以得出基于串級模糊自適應PID的控制系統對橋式起重機的吊重防搖系統具有較好的控制作用。

5 結論

本文基于拉格朗日方程建立橋式起重機的狀態空間模型，利用Matlab/Simulink進行仿真研究，在傳統串級PID控制的基礎上提出將原來內環單純的PID控制替換為模糊自適應PID控制，同時通過貝加萊防搖控制平臺完成實驗驗證得出基于串級模糊自適應PID防搖控制系統的控制效果較好，對實際工業防搖控制系統的應用具有一定的指導作用。

參考文獻：

[1] 徐軍,汪偉剛.起重機防搖控制研究綜述[J].造船技術,2013,(2):25-30.

[2] 王璐,常中龍,袁哲,et al.橋式起重機防搖控制系統數學建模方法研究[J].起重運輸機械,2016,(9):1-5.

[3] 劉為,瞿軍,袁湛,et al.龍門吊車防搖模糊控制研究[J].機械制造,2009,47(2):16-8.

[4] 單磊,費國.防搖控制系統在集裝箱起重設備中的研究與應用[J].起重運輸機械,2011,(10): 51-5.

[5] 胡艷麗,劉團結,季學斌,et al.基于模糊的的橋式起重機智能防擺控制研究[J].數字技術與應用,2014,14(7):22.

[6] 禹建麗,張宗偉,楊用增.基于自適應模糊神經網絡的起重機吊擺防搖控制[J].電氣自動化,2009,31(2):28-9.

[7] 王佳奕.岸邊集裝箱起重機自動防搖控制的研究[D].上海交通大學,2012.

Research on anti swing control of crane based on cascade fuzzy adaptive PID

LIU Bin1, CHEN Hai-yun1

TP273.4

：A

：1009-0134(2017)08-0019-04

2017-04-17

劉斌（1990 -），男，研究生，研究方向為工業控制自動化。