水質檢測化驗誤差數據處理與分析

李偉晶

(遼寧省錦州水文局，遼寧 錦州 121000)

水質檢測化驗誤差數據處理與分析

李偉晶

(遼寧省錦州水文局，遼寧 錦州 121000)

水質監測與檢測是區域水資源保護工作中的重要一環。文章主要以遼寧省錦州市為例，對該研究區水質檢測化驗誤差數據處理與分析相關內容展開論述。文中首先針對水質檢測誤差分析中常用的兩大概念"真值與平均值"進行介紹，在此基礎上，分別對誤差與誤差類型、準確度與精密度等相關內容進行簡介，從而為本研究水質檢測化驗誤差數據處理、分析提供理論依據。

水質檢測；化驗；誤差；數據處理

0 前 言

水質檢測可保證水資源質量安全、可靠，它是保證農村地區飲用水健康的重要方式。但在水質檢測過程中，受主、客觀因素影響和制約，如農村地區檢測設備、技術方式等相對落后等，這些因素會在一定程度上嚴重干擾水質測定結果；再加上水質檢測過程中技術人員主觀失誤和責任意識不強，經常會導致水質檢測化驗數據出現誤差。所以，對水質檢測化驗誤差數據進行處理、分析尤為重要。通過水質檢測化驗數據誤差處理與分析，即可找到影響水質檢測結果的主要因素，以便控制干擾因子，消除不良影響，保證水質檢測結果準確、客觀與完整。

1 水質檢測化驗誤差數據處理與分析技術依據

1.1 水質檢測化驗誤差數據處理與分析中的真值與平均值

水質檢測化驗誤差數據處理與分析主要是以檢測數據誤差及其在運行中產生的相關影響為對象，確定水質最終檢測結果的精確性。從本質上而言，水質檢測化驗數據誤差是客觀存在的，只要保證誤差控制在合理范圍內，都是可行的。但誤差過大就會影響水質測定結果，不利于對研究區水質總體情況作出客觀判斷與分析[1]。而水質檢測數值是物理量的真實值，在水質檢測中一般無法得到真值，只能通過平均值代替水質檢測化驗真值；同時，水質測定次數有限，只能通過多次測定中取得的平均值作為近似測定結果，對水質狀況進行合理判斷。在水質測定中，常用的平均值主要分為算術平均值、均方根平均值、加權平均值、中位值、幾何平均值幾種。具體測定化驗誤差數據處理計算公式分別如下：

1)錦州市水質檢測化驗誤差數據處理與分析中的算術平均值計算：

公式如下：

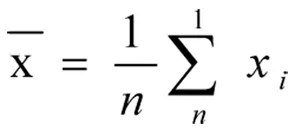
(1)

2)錦州市水質檢測化驗誤差數據處理與分析中的均方根平均值誤差計算：

公式如下：

(2)

3)錦州市水質檢測化驗誤差數據處理與分析中真值計算：

公式如下：

A=x±△x

(3)

4)錦州市水質檢測化驗誤差異常數據處理與取舍：

公式如下：

(4)

5)錦州市水質檢測化驗誤差數據處理與分析中合理判斷K值：

公式如下：

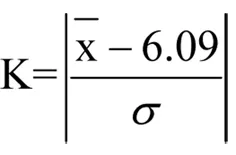
(5)

2.2 水質檢測化驗誤差數據處理與分析中的常見誤差與類型

水質檢測化驗中的誤差分為絕對和相對誤差2種。其中，絕對誤差是指水質檢測值與真實值之間的差值。因水質檢測真實值難以獲得。因此，在實踐中經常采用檢測值與平均值之間的差表示水質檢測絕對誤差。

在檢測過程中，只需將標準式樣中某成分實際含量作為該組分的真值，即可以此為標準對檢測誤差進行估算。對誤差分析準確度進行判斷時，經常采用相對誤差這一指標來衡量[2]。

其中，絕對誤差/平均值=相對誤差。

在對水質檢測化驗過程中產生的相關數據誤差進行分類，其中根據不同誤差產生成因，可將誤差分為不同種類，具體而言分為3種，分別是系統誤差、隨機誤差與過失誤差。這3種誤差主要是由測定中不確定性因素和技術操作人員操作不規范所導致。

2.3 水質檢測化驗誤差數據處理與分析中的準確度與精密度

對水質檢測化驗數據準確性進行分析，經常采用準確度與精確度兩大指標來衡量。其中，準確度是指水質測定值與真實值之間的偏差，其可反映系統誤差大小，通過相對誤差來表示。而水質檢測精密度主要是指在控制條件下，采用一個均勻試驗進行反復測定，以此得到重復數據即可隨機反映水質測定結果的準確性。這一指標可反映水質測定值與算術平均值之間的偏差程度。精密度是保證準確度的前提和基礎，只有消除了水質測定誤差，才能通過精密度表示水質測定準確度。而在水質測定結果分析中，先要通過對數據精密度進行考察，然后才能對其準確度進行分析，充分弄清二者關系有助于正確處理水質檢測化驗誤差數據[3]。

3 水質檢測化驗誤差數據處理與分析實踐應用

3.1 直接法

直接數據處理是指直接從儀表中讀取數據；而間接處理是指通過計算得到數據結果的方式。

1)水質檢測化驗誤差數據處理與分析中的單項測量值誤差。

在水污染環境檢測過程中，經常會受相關技術條件和設備因素制約。因此，難以對數據進行準確測量，只有經過多次循環，才能得到具體數值。這些數值往往是平均近似值，需結合實際對其進行修正。在處理中，對于誤差較小的結果只需結合儀表中的數據對其適當計算即可；而誤差較大的數據需按儀器上最小刻度的1/2作為單項測量最大絕對誤差。

2)水質檢測化驗誤差數據處理與分析中多次重復測量值誤差。

在水質測定結果分析中，為了得到準確數值，往往需經過多次重復測量與計算，用這些測量值的算術平均值即可近似度代替水質測量值的真值。其中，水質測量值的真值可表示為：

A=x±△x

(6)

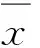
(7)

另外，測量值與算術平均值的差-偏差即可表示為：

dxi=xi-x

(8)

算術平均誤差即可表示為：

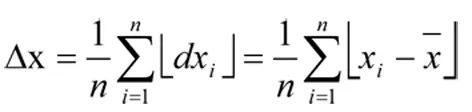
(9)

例如：在對錦州市2016年某研究區水質進行檢測過程中，通過10次循環測定，最終得到如下10組原水濁度測定結果，分別為0.490、0.471、0.475、0.492、0.473、0.480、0.468、0.492、0.476、0.451，

按照上述計算公式，即可得到：

錦州市水質濁度算術平均值為：

(10)

錦州市水質濁度算術平均誤差:

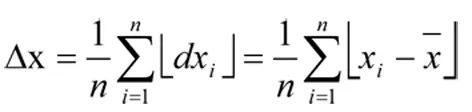
(11)

錦州市水質濁度真值為：

A=x±△x=錦州市水質濁度算術平均值±錦州市水質濁度算術平均誤差=0.4902±0.00083

(12)

即可確定錦州市水質濁度測定真值處于0.4902-0.00083這一區間內。

3.2 間接法

與直接法不同，水質檢測數據間接測量值主要是指將直接測量值代入不同計算處理公式得到的一種誤差分析法。間接測量值的準確性受直接測量結果與公式形式等因素影響。間接測量誤差主要是考察同一水質在不同誤差情況下相加得到的誤差情況。各項直接測量值絕對誤差之和=只含和、差運算間接測量值的絕對誤差；間接測量、直接測量值之間的函數關系含乘、除、乘方、開方等運算時，各直接測值相對誤差之和=相對誤差。當間接測量值計算公式只含加減運算時或含有乘、除、乘方、開方時，要分別先計算絕對誤差，再計算相對誤差或先計算相對誤差，后計算絕對誤差。

例如，在錦州市水質檢測化驗處理中，溶質直接測定量和使用分析天平測量的絕對誤差WB分別為0.3468g和0.0003g。溶劑水質量W A在臺秤上稱刻度為26g，絕對誤差=0.2g。置于60mL容量瓶中，容量瓶刻度絕對誤差、溶質與溶劑水觀測體積刻度分別為±0.06mL和V=26mL。則通過計算可得：

1)水溶質稱量相對誤差：

=ΔWB /WB=±0.0003/0.3468 =±1.5×10-3

2)水溶劑稱量的相對誤差：

=ΔWA /W A =±0.2/26 =±3×10-3

3)觀測體積相對誤差：

=ΔV/V =±0.06/26 =±3×10-3

由此可求得所配試劑的相對誤差

=ΔWB /WB+ΔWA /WA+ΔV/V

=(±1.5×10-3)+(±3×10-3)+(±3×10-3)

3.3 水質檢測化驗誤差數據處理與分析中的異常數據取舍

在水質檢測化驗數據處理分析中，經常需對異常數據進行取舍處理。通常采用的異常數據取舍方法有肖維涅準則。

例如：在錦州市水質檢測化驗處理中得到的一組PH實測數按照從大到小順序排列，分別為9.62、9.24、8.98、8.92、8.81、8.79、8.71、8.67、8.61、8.56、8.48、8.39、8.37、8.31、8.17、7.19。其中數據9.62和7.19分別為最大值和最小值，與其它數據之間存在異常，所以按照以下計算公式即可對異常數據進行取舍：

根據公式：

(13)

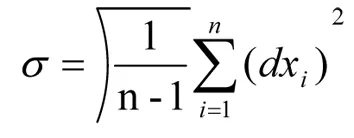
在上述計算基礎上，合理判斷K值：

(14)

通過查表“n與K的對應值”當n為16時，k=2.26,

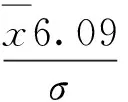
4 結 語

綜上可知，文章重點對該研究區水質檢測化驗誤差數據處理與分析方法進行闡述，文中提出了單項測量值的誤差分析、多次重復測量值的誤差分析、直接與間接測量值的誤差分析、異常數據取舍等水質化驗誤差數據處理與分析方法。實踐結果表明，直接計算法與間接計算法、基于肖維涅準則的異常數據取舍法，均可有效提高錦州市水質測定、化驗誤差數據處理精確性，大大提高數據分析科學性，從而為錦州市水質檢測結果分析提供了重要參考依據，上述方法值得應用與推廣。

[1]程曼曼.季節性肯達爾檢驗法在南灣水庫水質趨勢分析中的應用[J].河南水利與南水北調, 2012(16)：57-58.

[2]韓靜.汾河水庫水質趨勢分析[J].山西水利科技, 2009(01)：92-93，96.

[3]胡國華, 唐忠旺,肖翔群.季節性Kendall檢驗及其在三門峽水庫水質趨勢分析中的應用[J].地理與地理信息科學, 2004(03):86-88.

[4]朱佳佳.九龍江流域水環境狀況及治理對策初探[J].水利技術監督,2009(04):27-29.

1007-7596(2017)08-0056-03

2017-08-16

李偉晶(1964-)，男，遼寧錦州人，工程師，從事水質化驗、監督執法等工作。

X832

：B