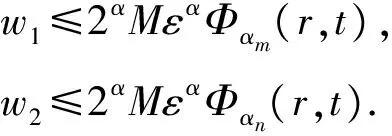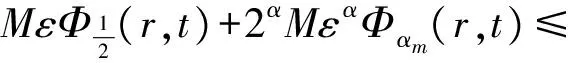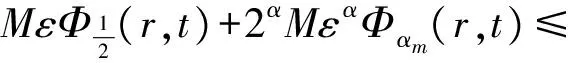一類二維強耦合波動方程組經(jīng)典解的生命跨度的下界研究
王虎生, 孫海霞, 楊 晗
(西南交通大學 數(shù)學學院, 四川 成都 611756)
一類二維強耦合波動方程組經(jīng)典解的生命跨度的下界研究
王虎生, 孫海霞, 楊 晗*
(西南交通大學 數(shù)學學院, 四川 成都 611756)
考慮二維強耦合波動方程組的柯西問題,在初值較小且具有緊支集的前提下,通過半群的方法,得到方程組經(jīng)典解的生命跨度下界估計,改進了前人已有的結(jié)果.
強耦合系統(tǒng); 波動方程; 經(jīng)典解; 生命跨度下界
本文考慮如下的二維波動方程組柯西問題
(1)
其中,ε是充分小正常數(shù),f1、f2、g1、g2是一光滑函數(shù),p1,p2,q1,q2>1.
先回顧一下相關的結(jié)論,對于所熟知的單個方程
utt-Δu=|u|p
(2)
的柯西問題有如下結(jié)論:當n≥2,在初值足夠小且具有緊支集時,存在一個臨界指p0(n),當p>p0(n)時該方程存在整體解,1 當n=2時,R. Glassey[1]得到該猜想的爆破情形,R. Glassey[2]得到該猜想的整體解情形;當n=3時,F(xiàn). John[3]同時得到該猜想的爆破和整體解的情形;當n≥4時,爆破結(jié)論的證明由T. Sideris[4]得到.關于該猜想的整體解:Zhou Y.[5]得到n=4的情形,H. Lindblad等[6]得到3≤n≤8的情形,并最終由V. Georgiev等[7]延拓到n>8的情形. H. Kubo等[8]在n=2,3且初值滿足某種條件的前提下,得知方程(2)經(jīng)典解的生命跨度上界估計 (3) 二維波動方程組的研究則開始于20世紀90年代,對于弱耦合系統(tǒng)的方程組 (4) 的初值問題,有如下研究成果: (5) (6) 的初值問題的研究成果如下: 當n=1時,無論初值有多小,方程(2)的柯西問題的經(jīng)典解總會爆破. Zhou Y.[12]得到n=1時對于任意的p>1解的生命跨度T(ε)的上界和下界估計 (7) (x,t)∈Rn×[0,T],m>0. (8) 其中,p>1,φ(s)=slog(2+s),s≥0. 基于上述結(jié)果,本文也考慮在空間維數(shù)n=2時,在非線性項中引入加權項后討論方程(8)的柯西問題,希望得到類似Strauss猜想的結(jié)論:存在一臨界指數(shù)αm(2),當α>αm(2)整體解存在,相反,解將在有限時間內(nèi)爆破.同時,由于非線性項中引入了衰減的加權項,希望得到的結(jié)果比沒有衰減加權項時要好;另一方面,加權的強耦合波動方程組在取特殊參數(shù)的前提下等價于單個的波動方程(8).由此,有必要研究強耦合波動方程組(1)的柯西問題的生命跨度. 定理 1 對初始條件作如下假設: 1) 具有緊支集,即存在R>0,有 supp(fj(x),gj(x))={x:|x|≤R}; (9) 2) 存在正常數(shù)c,當 0<ε<1. (10) 注 1 在初始條件滿足(9)和(10)式的基礎上,取m=0,驗證了方程組(8)(或方程(2))經(jīng)典解的相關結(jié)論.本文得到了相應的下界,文獻[8]得到方程(2)解的上界估計.鑒于其形式上的一致性,進而形成了方程(2)經(jīng)典解的門檻估計,即 利用降維法和齊次化原理,方程組(1)柯西問題的解可記為 (11) 其中,u0、v0是二維齊次波動方程 (12) 的解,解的非齊次部分w1、w2的解的表達式分別為 (13) (14) 其中,y=x+ρw,|w|=1,x,y,w∈R2. 引理 1 假設f1、f2、g1、g2滿足(9)和(10)式,設u0、v0是齊次方程(12)的解,則有 證明過程參考文獻[2]. 引理 2 已知y=x+ρw,x,w∈R2,ρ為半徑,|w|=1,λ=|y|, (15) 證明 由λ=|y|得到 θ∈[0,π],則 那么 由于h(λ,ρ,r)=h(ρ,λ,r),于是得到(15)式. 接下來,為了方便起,借助文獻[10]引入如下記號 引理3 記(u,v)∈C2(R2×[0,T*(ε)))×C2(R2×[0,T*(ε)))為方程組(1)柯西問題的解,Bρ(x,t)是球心為(x,t)半徑為ρ的球體,那么存在x0∈R2使得對于任意的ρ>0滿足在Bρ(x0,t)∩(R2×[0,T*(ε)))里,|u(x,t)|或者|v(x,t)|無界. 證明過程類似文獻[10]的定理2.2. 引理4 定義積分 Iz(r,t)= z(λ,s)=(1+s+λ)1+k(1+|λ-s|)1+μ, k∈R,μ∈R,那么有 Iz(r,t)≤CΦk(r,t)Ψμ(t+r), 這里C為常數(shù). 證明過程參考文獻[10]的命題3.1. 首先,根據(jù)半群理論及壓縮映射原理,易知方程組(1)局部解的存在性.引理1建立了方程組齊次部分解的估計,接下來需要建立方程組非齊次部分解的估計. 命題 1 如果k∈R,μ∈R,T>0,C為常數(shù),對于(x,t)∈R2×[0,T),有 (1+||y|-s|)1+μ|u|p1|v|q1}, (16) (1+||y|-s|)1+μ|u|p2|v|q2}. (17) 證明 根據(jù)(13)式得 其中 z(|y|,s)=(1+s+|y|)1+k(1+||y|-s|)1+μ, S(s,z)= 根據(jù)引理2,令|y|=λ,那么 用Iz(r,t)定義如下積分 根據(jù)引理4得到(16)式,同理可得(17)式. 注意到 (18) 那么根據(jù)(18)式可知,對于(x,t)∈R2×[0,T)有 (19) (20) 圖 1 p1-q1 區(qū)域圖 對于w1,w2∈C(R2×[0,T)),假設 w1≤2α+1MεαΦαm(r,t), w2≤2α+1MεαΦαm(r,t) (21)成立,接下來根據(jù)區(qū)域的劃分按3種情況分類討論. 命題 2 令w1,w2∈C(R2×[0,T)),k>0,μ∈R,m∈[0,1],存在ε0=ε0(p1,q1,p2,q2,m,n),使得0<ε≤ε0,若α>αm(2),那么有: w1≤2αMεαΦαm(r,t), (22) w2≤2αMεαΦαm(r,t). (23) 接下來,w1、w2滿足(18)式,在假設(21)式成立的前提下,將其代入(19)和(20)式中,首先對(19)式右邊4項分別進行估計. (i) 估計(19)式右邊第一項 CMαεαΦk(r,t)Ψμ(t+r)× 于是當滿足CMα≤M時,得到 (24) (ii) 接下來估計(19)式右邊第二項 2(α+1)q1CMαεp1+αq1Φk(r,t)Ψμ(t+r)× 2(α+1)q1CMαεp1+αq1Φk(r,t)Ψμ(t+r)× 存在ε,當0<ε≤ε0,滿足2(α+1)q1CMαεp1+αq1-α≤M時,得到 (25) (iii) 接下來估計不等式(19)右邊第三項 2(α+1)p1CMαεαp1+q1Φk(r,t)Ψμ(t+r)× 2(α+1)p1CMαεαp1+q1Φk(r,t)Ψμ(t+r)× 于是存在ε,當0<ε≤ε0,滿足 2(α+1)p1CMαεαp1+q1-α≤M 時,得到 (26) (iv) 接下來估計不等式(19)右邊第四項 2(α+1)αCMαεα2Φk(r,t)Ψμ(t+r)× 2(α+1)αCMαεα2Φk(r,t)Ψμ(t+r)× (1+||y|-s|)1+μΦαm(r,t)α}. (1+||y|-s|)1+μΦαm(r,t)α}≤1. 于是存在ε,當0<ε≤ε0,滿足2(α+1)α×AMαεα2-α≤M時,得到 (27) 最終,將(24)~(27)式代入到(19)式中,得到(22)式.類似地,對(20)式右側(cè)的4項進行估計,可以得到(23)式. 命題3 令w1,w2∈C(R2×[0,T)),k>0,μ∈R,m∈[0,1],若α=αm(2),存在一正常數(shù)M*,當εα2-α×(1+log(1+T))≤M*,則存在正常數(shù)ε0=ε0(p1,q1,p2,q2,m,M,R),對任意的ε,當0<ε≤ε0時,有: w1≤2αMεαΦαm(r,t), (28) w2≤2αMεαΦαm(r,t). (29) 證明 首先,由于α=αm(2),選擇如下區(qū)域{(p1,q1)|{p1>1}∩{q1>1}∩{data 3}}(p2-q2曲線與之一樣),顯然 w1、w2滿足(18)式,在假設(21)式成立的前提下,將其代入(19)和(20)式中,其中對(19)式右邊前3項與命題2類似,接下來對最后一項進行估計, 2(α+1)αCMαεα2Φk(r,t)Ψμ(t+r)× 2(α+1)αCMαεα2Φk(r,t)Ψμ(t+r)× (1+||y|-s|)1+μΦαm(r,t)α}. (1+||y|-s|)1+μΦαm(r,t)α}≤1. 于是存在ε,當0<ε≤ε0,滿足2(α+1)αCMαεα2-α(1+log(1+T))≤M時.換言之,存在與ε無關的常數(shù)M*,當εα2-α(1+log(1+T))≤M*,得到 (30) 將(19)式右邊前3項及(30)式的估計代入(19)式得到(28)式,同理可以得到(29)式. 命題 4 令w1,w2∈C(R2×[0,T)),k>0,μ∈R,m∈[0,1],若α<αm(2),存在正常數(shù)M*,使得εα2-α(1+T)-N(α,m)≤M*,那么存在正常數(shù)ε0=ε0(p1,q1,p2,q2,m,M,R),對任意的ε,使得0<ε≤ε0,有: w1≤2αMεαΦαm(r,t), (31) w2≤2αMεαΦαm(r,t). (32) 證明 由于α<αm(2),選擇區(qū)域 {(p,q)|{p>1}∩{q>1}∩{areaE}} (p2-q2曲線與之一樣),易知 w1、w2滿足(18)式,在假設(21)式成立的前提下,將其代入(19)和(20)式中,其中對(19)式右邊前3項與命題2類似,接下來對最后一項進行估計, 2(α+1)αCMαεα2Φk(r,t)Ψμ(t+r) (1+||y|-s|)1+μw1p1w2q1}≤ 2(α+1)αCMαεα2Φk(r,t)Ψμ(t+r)× (1+||y|-s|)1+μΦαm(r,t)α}. (1+||y|-s|)1+μΦαm(r,t)α}≤1. 于是存在ε,當0<ε≤ε0,滿足 2(α+1)αCMαεα2-α(1+T)-N(α,m)≤M 時,換言之,存在與ε無關的常數(shù)M*,當 εα2-α(1+T)-N(α,m)≤M*, 得到 (33) 將(19)式右邊前3項及(33)式的估計代入(19)式得到(31)式,同理可以得到(32)式. 本文目標是獲得w1、w2的上界,那么當(x,t)∈R2×[0,T),在滿足先驗假設(21)式成立的前提下,進而可知(u,v)的解存在,定義T0(ε)為所有滿足如上T的上確界. 當|x|≥t+R時,u(x,t)=v(x,t)=0,那么 (34) 接下來,分3種情況討論: 1) 當α>αm(2)時,假設T*(ε)<∞,在(34)式成立的前提下,得到 |u(x,t)|=|u0(x,t)|+|w1(x,t)|≤ |v(x,t)|=|v0(x,t)|+|w2(x,t)|≤ 根據(jù)引理3可以得到T0(ε)≤T*(ε).根據(jù)T0(ε)的定義,可以得知存在x0∈R2使得 |w1(x,t)|≥2α+1MεαΦαm(r,t), t∈[T0(ε),T*(ε)). (35) 另一方面,從命題2得知|w1(x,t)|≤2pMεpΦp(r,t),進而可以得到矛盾,于是得到T*(ε)=∞. 2) 當α=αm(2)時,(α<αm(2)的情形與之類似)根據(jù)命題3,知道存在一正常數(shù)M*,當 εα2-α(1+log(1+T))≤M* (36) 時,對于(x,t)∈R2×[0,T)時,有 w1≤2αMεαΦαm(r,t), (37) w2≤2αMεαΦαm(r,t). (38) 考慮(36)式,求解得到 T1(ε)=exp(M*ε-α(α-1)-1)-1. 假設T0(ε) 于是(u(x,t),v(x,t))有界,根據(jù)引理3,知道 T0(ε) 更進一步,根據(jù)(28)和(29)式,得到一個比假設(21)式更窄的估計,這是一個矛盾,于是可知 T0(ε)≥T1(ε). 最終得到定理1中的α=αm(2)情形. [1] GLASSEY R. Finite-time blow-up for solutions of nonlinear wave equations[J]. Math Z,1981,177(3):323-340. [2] GLASSEY R. Existence in the large foru=F(u) in two dimensions[J]. Math Z,1981,178(2):233-261. [3] JOHN F. Blow-up of solutions of nonlinear wave equations in three space dimensions[J]. Manuscripta Math,1979,28(1):235-265. [4] SIDERIS T. Nonexistence of global solutions to semilinear wave equations in high dimen sions[J]. Commum Partial Differ Equations,1984,52(3):378-406. [5] ZHOU Y. Cauchy problem for semilinear wave equations with small data in four space dimensions[J]. J Differ Equations,1995,34(8):135-144. [6] LINDBLAD H, SOGGE C D. Long-time existence for small amplitude semilinear wave equations[J]. Am J Math,1997,118(5):1047-1135. [7] GEORGIEV V, LINDBLAD H, SOGGE C D. Weighted Strichartz estimate and global existence for semilinear wave equations[J]. Am J Math,1997,119(6):1291-1319. [8] KUBO H, OHTA M. On the Global Behavior of Classical Solutions to Coupled Systems of Semilinear Wave Equations, “New Trend in the Theory of Hyperbolic Equations”[M]. Birkhause:Advances in Partial Differential Equations,2005:120-133. [9] SANTO D, GEORGIEV V, MITIDIERI E. Global existence of the solutions and formation of sing-Ularities for a class of hyperbolic system[J]. Progess in Nonl Differ Eqns Appl,1997,32:117-140. [10] FLAVIANO M D. Lower bounds of the life span of classical solutions to a system of semilinear wave equations in two space dimension[J]. J Math Anal Appl,2003,281(1):22-45. [11] KUBO H, OHTA M. blow-up for systems of semilinear wave equations in two space dimension[J]. Hokkaido Math J,2006,2006(35):699-717. [12] ZHOU Y. Life span of classical solution toutt-uxx=|u|1+α[J]. Chin Ann Math,1992,B13(2):230-243. [13] KUBO H, OSAKA A, YAZICI M. Global existence and blow-up for wave equations with weighted nonlinear terms in one space dimension[J]. Interdisciplinary Information Sciences,2013,19(2):143-148. [14] WAKASA K. The life span of solutions to wave equations with weighted nonlinear terms in one space dimension[J]. Analysis PDES,2014:arXiv:1409.5877v1. [15] ZHOU Y. Life span of classical tou=|u|pin two space dimension[J]. Chin Ann Math,1993,B14(2):225-236. 2010 MSC: 35L05; 35L70 (編輯 陶志寧) The Lower Bounds of the Life Span for the Classical Solutionsfor a System of the Strong Coupled Wave Equations in Two Space Dimension WANG Husheng, SUN Haixia, YANG Han (SchoolofMathematics,SouthwestJiaotongUnivesity,Chengdu611756,Sichuan) In this paper, we consider the Cauchy problem for a system of strong coupled wave equations. Under the assumption of small initial data with compact supportset, using the semigroup method we study the lower bounds of the life span of the solutions and promote the relative known results. strong coupled system; wave equations; classical solution; lower bounds of the life span 2016-08-25 國家自然科學基金(71572156) O175.6 A 1001-8395(2017)04-0442-08 10.3969/j.issn.1001-8395.2017.04.003 *通信作者簡介:楊 晗(1969—),男,教授,主要從事偏微分方程的研究,E-mail: hanyang 95@263.net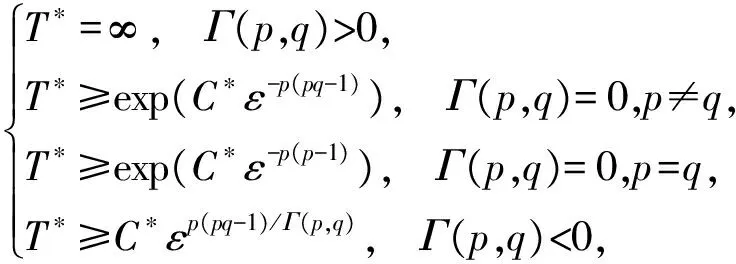
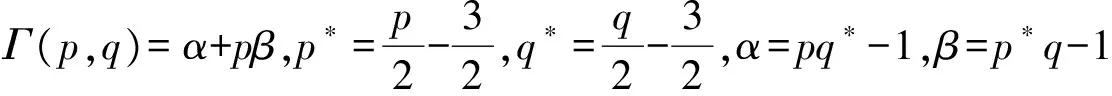
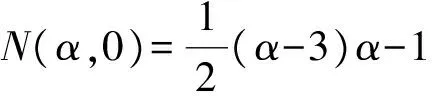
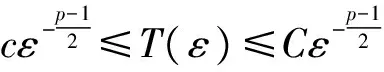
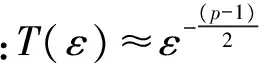
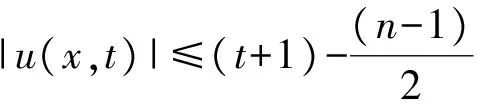
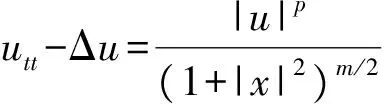
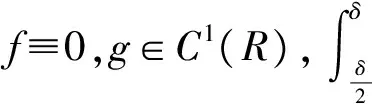
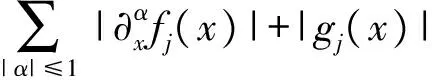
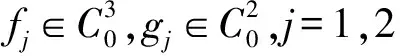
1 預備知識
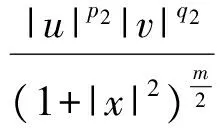
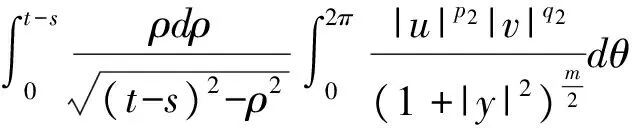
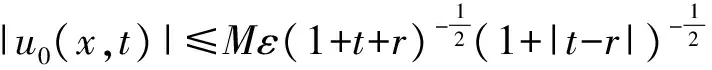
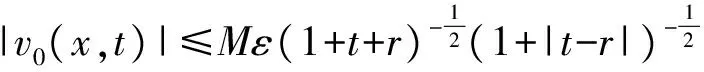
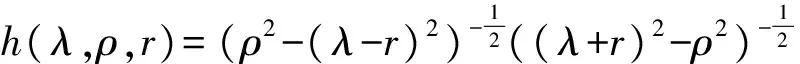
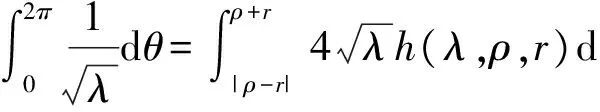
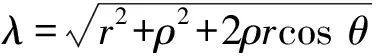
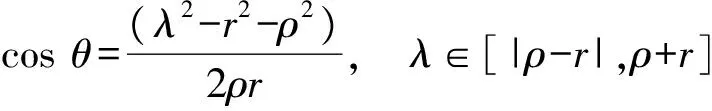
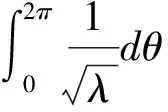
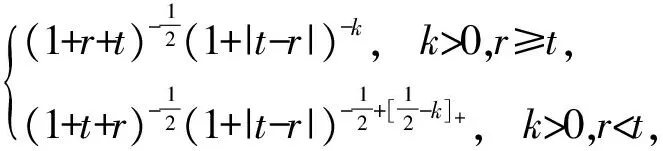
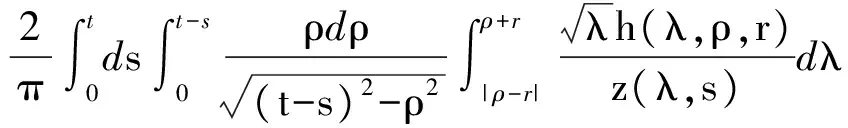
2 建立方程組非齊次部分解的基本估計
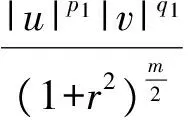
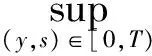
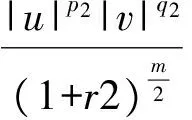
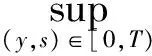
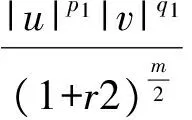
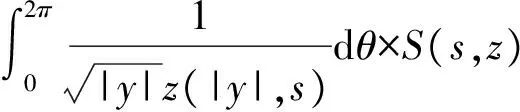
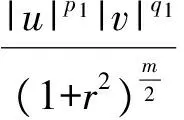
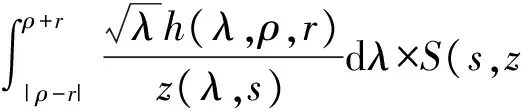
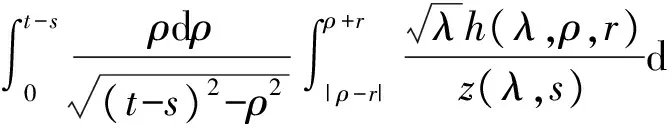
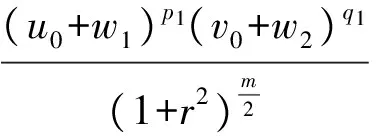
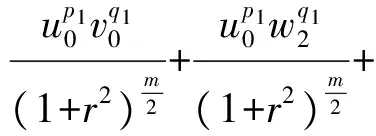
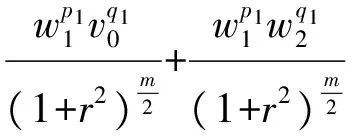
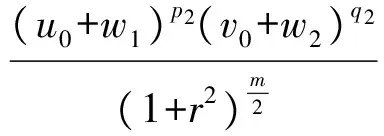
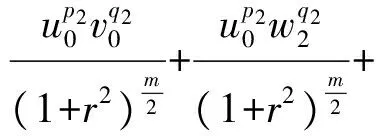
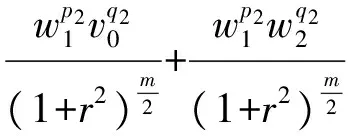
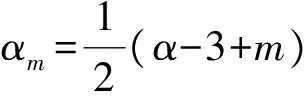
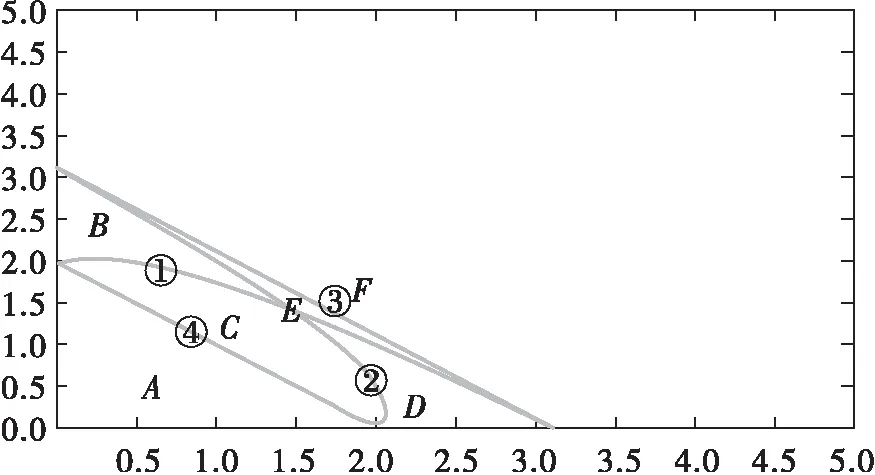
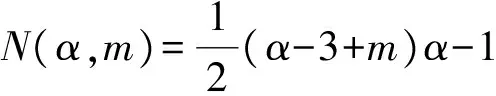
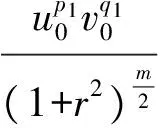
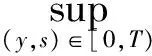
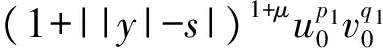
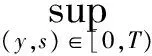
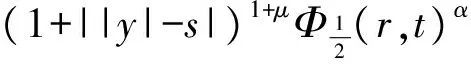
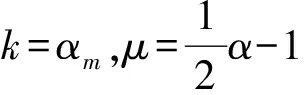
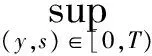
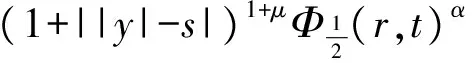
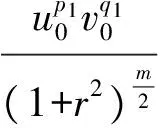
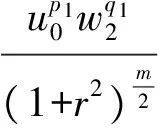
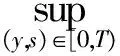
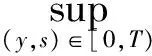
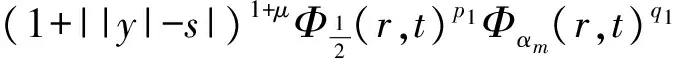
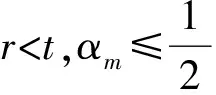
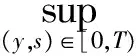
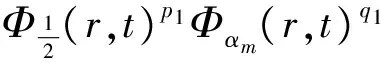
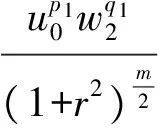
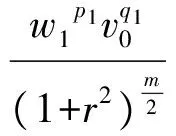
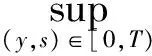
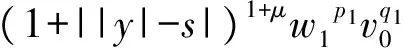
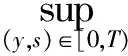
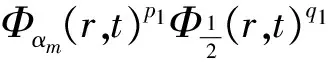
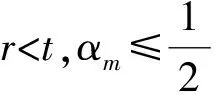
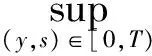
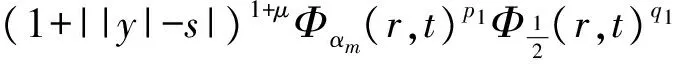
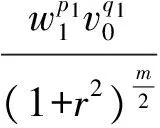
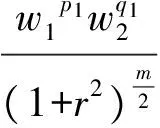
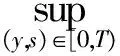
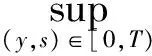
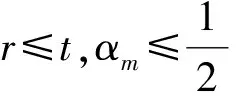
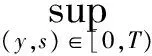
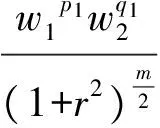
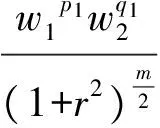
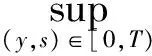
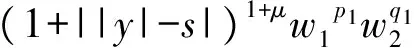
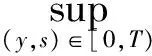
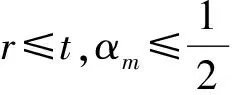
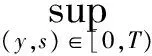
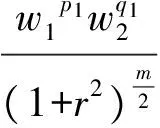
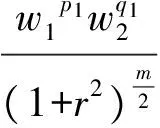
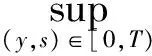
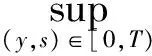
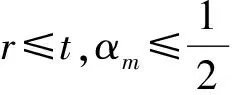
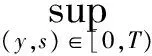
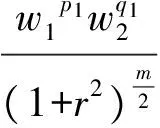
3 建立方程組非齊次部分解的先驗估計