兩點(diǎn)激勵(lì)中相關(guān)系數(shù)的影響

農(nóng)紹寧，趙懷耘

?

兩點(diǎn)激勵(lì)中相關(guān)系數(shù)的影響

農(nóng)紹寧，趙懷耘

（中國(guó)工程物理研究院 總體工程研究所，四川 綿陽(yáng) 621900）

目的用譜函數(shù)分析的方式，推導(dǎo)結(jié)構(gòu)在兩點(diǎn)激勵(lì)下的隨機(jī)振動(dòng)響應(yīng)的計(jì)算公式。方法通過(guò)互譜與相關(guān)系數(shù)的關(guān)系，討論結(jié)構(gòu)在兩點(diǎn)激勵(lì)下的響應(yīng)特點(diǎn)。結(jié)果對(duì)于線性結(jié)構(gòu)，不同相關(guān)系數(shù)的兩點(diǎn)激勵(lì)下結(jié)構(gòu)激發(fā)的模態(tài)效果不同，隨著相關(guān)系數(shù)的增大，結(jié)構(gòu)的響應(yīng)在相鄰的諧振峰上，出現(xiàn)增大、減小交替出現(xiàn)的現(xiàn)象。結(jié)論相關(guān)系數(shù)對(duì)結(jié)構(gòu)響應(yīng)影響的特點(diǎn)，應(yīng)該引起工程結(jié)構(gòu)設(shè)計(jì)人員的重視。

兩點(diǎn)激勵(lì)；相關(guān)系數(shù)；隨機(jī)振動(dòng)

兩點(diǎn)激勵(lì)是多維激勵(lì)的一種方式。對(duì)于大尺寸結(jié)構(gòu)來(lái)說(shuō)，通常振動(dòng)環(huán)境下結(jié)構(gòu)前后端受到的激勵(lì)差異較大，利用多臺(tái)振動(dòng)器對(duì)試件進(jìn)行多維振動(dòng)激勵(lì)方式是更為合理、有效的一種模擬試驗(yàn)方法。GJB 150.16A—2009中對(duì)組合式飛機(jī)外掛實(shí)驗(yàn)也提出了多激勵(lì)點(diǎn)的要求[1]。由于多維振動(dòng)與工程實(shí)際關(guān)系密切，自20世紀(jì)60、70年代出現(xiàn)以來(lái)，就涌現(xiàn)出許多文獻(xiàn)對(duì)其進(jìn)行了研究綜述。文獻(xiàn)[2]討論了多軸振動(dòng)環(huán)境試驗(yàn)條件的定義、技術(shù)關(guān)鍵以及多軸振動(dòng)臺(tái)和振動(dòng)控制系統(tǒng)的介紹、應(yīng)用。文獻(xiàn)[3]闡述了多維振動(dòng)試驗(yàn)方法的原理、試驗(yàn)條件定義和試驗(yàn)控制算法。還有許多文獻(xiàn)[4—7]對(duì)大結(jié)構(gòu)尺寸的具體工程結(jié)構(gòu)進(jìn)行了數(shù)值仿真和實(shí)驗(yàn)，結(jié)果表明多維振動(dòng)下結(jié)構(gòu)的響應(yīng)相對(duì)于一致激勵(lì)有明顯的差異，總體上使結(jié)構(gòu)的響應(yīng)更為復(fù)雜。Hao[8]也利用他自己提出的相干函數(shù)模型計(jì)算了圓拱的多點(diǎn)輸入響應(yīng)，發(fā)現(xiàn)如果忽略地震動(dòng)之間的相干，則求得結(jié)構(gòu)的響應(yīng)有時(shí)偏高，有時(shí)偏低，但未能給出普遍的規(guī)律。

文中基于隨機(jī)振動(dòng)的理論，用譜函數(shù)分析的方式，推導(dǎo)結(jié)構(gòu)在兩點(diǎn)激勵(lì)下的隨機(jī)振動(dòng)響應(yīng)。利用互譜與相關(guān)系數(shù)的關(guān)系，討論了結(jié)構(gòu)在兩點(diǎn)激勵(lì)下不同相關(guān)系數(shù)的響應(yīng)特點(diǎn)，認(rèn)為相關(guān)系數(shù)對(duì)結(jié)構(gòu)的響應(yīng)有較大的影響，給出了一些有意義的結(jié)論。

1 兩點(diǎn)激勵(lì)隨機(jī)振動(dòng)響應(yīng)譜

為簡(jiǎn)化分析，以長(zhǎng)度為的簡(jiǎn)支均勻梁位移響應(yīng)為例說(shuō)明，如圖1、圖2所示。

圖1 左支座基礎(chǔ)激勵(lì)

圖2 右支座基礎(chǔ)激勵(lì)

對(duì)于圖1左支座基礎(chǔ)激勵(lì)，左支座基礎(chǔ)位移為0L時(shí)，桿長(zhǎng)處?kù)o態(tài)位移為；對(duì)于圖2右支座基礎(chǔ)激勵(lì)，右支座基礎(chǔ)位移為0R時(shí)，桿長(zhǎng)處?kù)o態(tài)位移為。

使用相對(duì)位移，即設(shè)相對(duì)位移為，動(dòng)力學(xué)方程為：

式中：為單位長(zhǎng)度質(zhì)量；為阻尼系數(shù)；為彎曲剛度；為第階模態(tài)。

質(zhì)量歸一化的模態(tài)為：

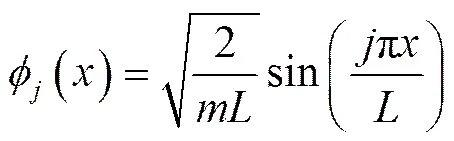
以左端為例：

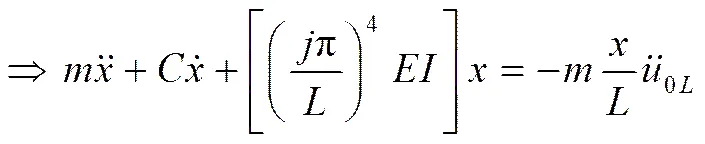
應(yīng)用模態(tài)正交性（仍用變量表示）：

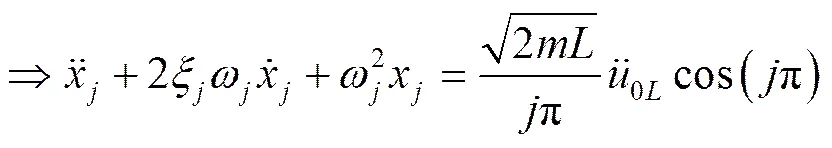
同理，對(duì)于右端：

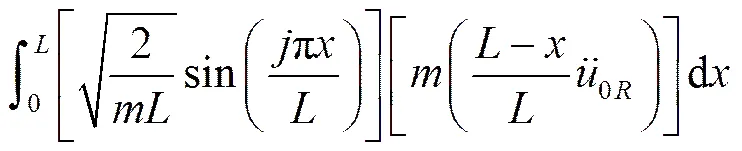
應(yīng)用杜哈曼積分：

方程的解為：

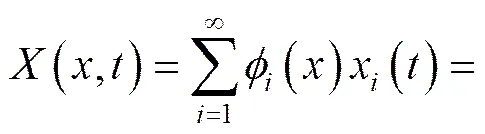
方程兩邊取相關(guān)函數(shù)：

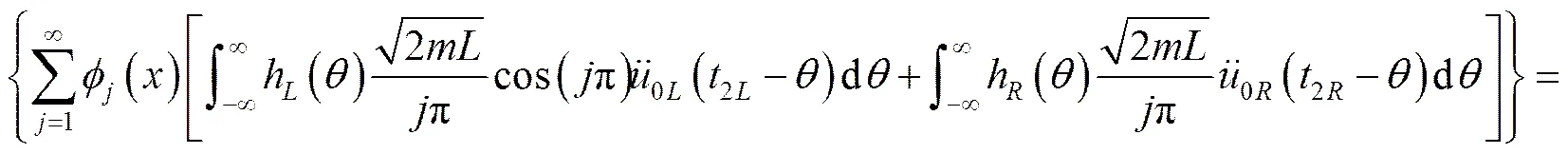
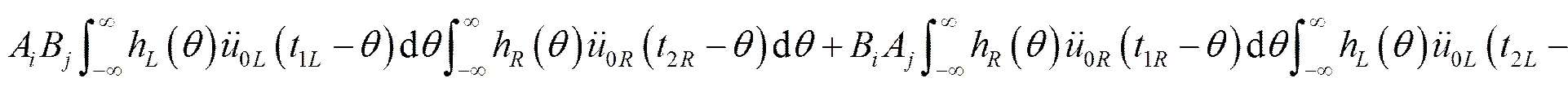
方程兩邊做傅里葉變換：

其中：

，，，，

式中：“*”代表共軛；S()為左端輸入加速度譜；S()為右端輸入加速度譜；S()和S()為兩端輸入加速度互譜。

2 互相關(guān)系數(shù)與互譜

每個(gè)激勵(lì)力函數(shù)，因?yàn)槭请S機(jī)過(guò)程()，在不同的時(shí)刻值是隨機(jī)變量，總有自己的相關(guān)函數(shù)，也就是自相關(guān)函數(shù)R()。

同理，兩個(gè)隨機(jī)過(guò)程()和()，它們?cè)诓煌臅r(shí)刻值是隨機(jī)變量，可以定義這兩個(gè)隨機(jī)變量函數(shù)的二階聯(lián)合矩：

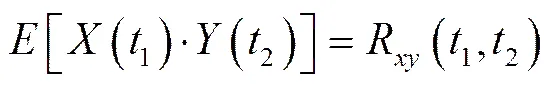
式中：R(1,2)為隨機(jī)過(guò)程()和()的互相關(guān)函數(shù)。

定義無(wú)量綱的標(biāo)準(zhǔn)互相關(guān)函數(shù)：

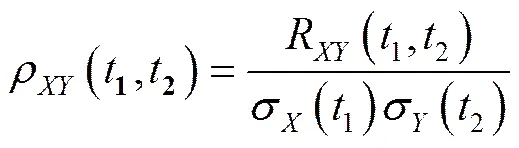
式中：σ(1)，σ(2)為隨機(jī)過(guò)程()和()的標(biāo)準(zhǔn)方差。

若互相關(guān)函數(shù)ρ(1,2)不恒等于零，則隨機(jī)過(guò)程()和()是相關(guān)的，若互相關(guān)函數(shù)ρ(1,2)恒等于零，則隨機(jī)過(guò)程()和()是不相關(guān)的。

對(duì)于各態(tài)歷經(jīng)的隨機(jī)過(guò)程，隨機(jī)過(guò)程()和()的標(biāo)準(zhǔn)方差不隨時(shí)間變化，為一個(gè)確定的值σ和σ。隨機(jī)過(guò)程()和()的互相關(guān)函數(shù)R(1,2)為時(shí)間差=2－1的函數(shù)，當(dāng)時(shí)間差固定時(shí)，互相關(guān)函數(shù)R(1,2)為一確定的值R。因此，同隨機(jī)變量相似，互相關(guān)函數(shù)為時(shí)間差的函數(shù)。

對(duì)比相干系數(shù)：

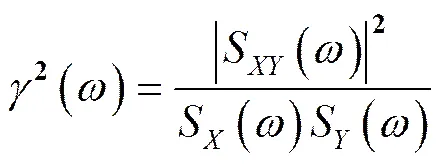
兩者是相似的，其中S()為R()的傅里葉變換。

因此相干系數(shù)也可以表征兩個(gè)各態(tài)歷經(jīng)隨機(jī)過(guò)程()和()的相關(guān)程度。一般來(lái)說(shuō)，相關(guān)程度越高，相干系數(shù)值越大，S()的值也較大。

3 互相關(guān)系數(shù)的影響

忽略≠的交叉項(xiàng)影響，響應(yīng)簡(jiǎn)化為：

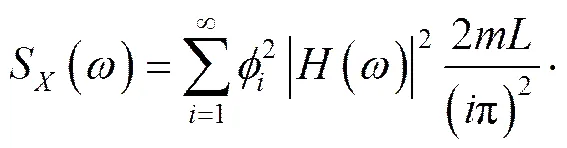
可見(jiàn)，響應(yīng)與模態(tài)階數(shù)有關(guān)，還與互譜S()的大小有關(guān)。特別的，當(dāng)兩點(diǎn)激勵(lì)完全相關(guān)時(shí)，則，響應(yīng)。在時(shí)，響應(yīng)為0。

4 工程實(shí)例

對(duì)某掛框式夾具進(jìn)行了兩點(diǎn)激勵(lì)振動(dòng)實(shí)驗(yàn)[9]。掛框式夾具兩點(diǎn)激勵(lì)振動(dòng)試驗(yàn)安裝狀態(tài)如圖3所示，測(cè)點(diǎn)布局如圖4所示。

圖3 掛框式夾具兩點(diǎn)激勵(lì)振動(dòng)實(shí)驗(yàn)安裝狀態(tài)

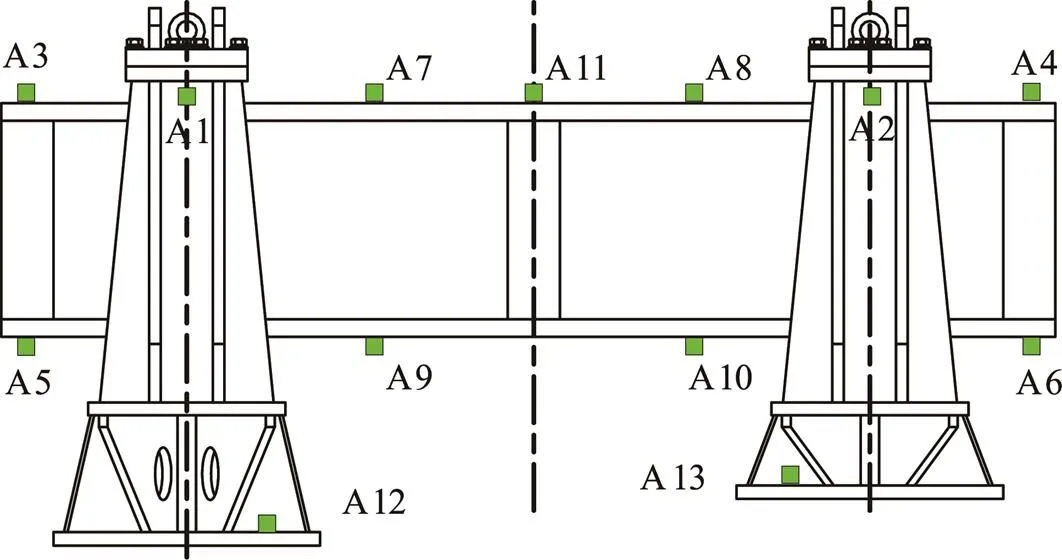
圖4 掛框式夾具兩點(diǎn)激勵(lì)振動(dòng)實(shí)驗(yàn)加速度測(cè)點(diǎn)布局

分別設(shè)置了互譜S()為0.0，0.3，0.5，0.9，以結(jié)構(gòu)上A5測(cè)點(diǎn)為例，不同的互譜值，即不同的相關(guān)系數(shù)下響應(yīng)見(jiàn)圖5。在其中的一個(gè)諧振峰上，隨著相關(guān)系數(shù)的增大，響應(yīng)值越大；而在相鄰的諧振峰上，隨著相關(guān)系數(shù)的增大，響應(yīng)值越小。

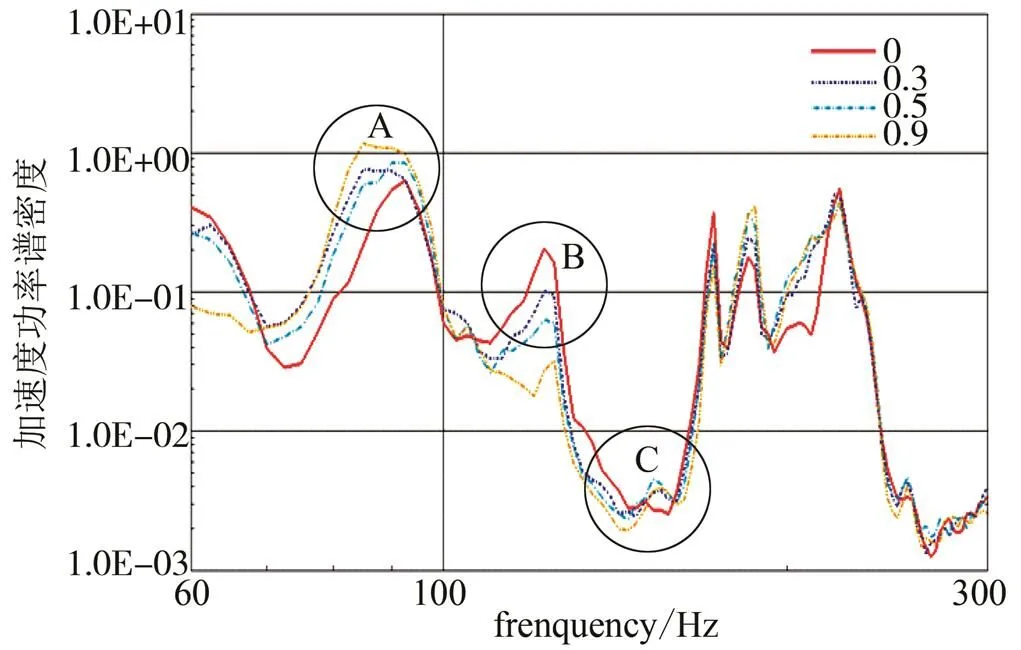
圖5 不同相關(guān)系數(shù)A5測(cè)點(diǎn)響應(yīng)

根據(jù)理論計(jì)算結(jié)果，結(jié)構(gòu)在143 Hz附近有諧振響應(yīng)，但結(jié)構(gòu)上（例如A5測(cè)點(diǎn)）在143 Hz附近響應(yīng)很小（見(jiàn)圖5C處），對(duì)應(yīng)了cos(π)= －1時(shí)的結(jié)果，如圖6所示。

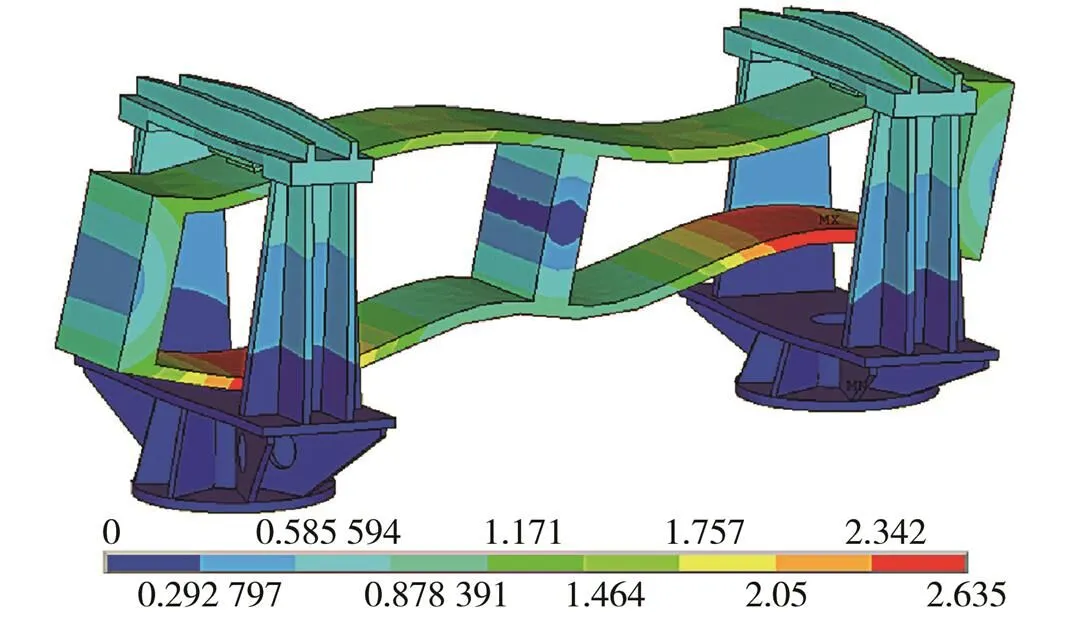
圖6 143 Hz模態(tài)響應(yīng)

5 結(jié)語(yǔ)

文中利用譜函數(shù)的形式，給出了兩點(diǎn)隨機(jī)激勵(lì)下結(jié)構(gòu)響應(yīng)的一些特點(diǎn)。從相關(guān)系數(shù)方面分析了結(jié)構(gòu)響應(yīng)差異的這一因素。隨著相關(guān)系數(shù)的增大，結(jié)構(gòu)在相鄰的諧振峰上，響應(yīng)隨之增大、減小交替出現(xiàn)。在激勵(lì)譜滿(mǎn)足一定的條件下，結(jié)構(gòu)響應(yīng)可能在某些模態(tài)的響應(yīng)為0。盡管提倡采用多點(diǎn)激勵(lì)的方式以利于激發(fā)出更多的結(jié)構(gòu)模態(tài)響應(yīng)，但也可能出現(xiàn)模態(tài)響應(yīng)為0的現(xiàn)象。兩點(diǎn)激勵(lì)振動(dòng)響應(yīng)的這些特點(diǎn)可為工程結(jié)構(gòu)設(shè)計(jì)人員提供參考。

[1] GJB 150.16A—2009 軍用裝備實(shí)驗(yàn)室環(huán)境試驗(yàn)方法第16部分: 振動(dòng)試驗(yàn)[S].

[2] 夏益霖. 多軸振動(dòng)環(huán)境試驗(yàn)的技術(shù)?設(shè)備和應(yīng)用[J]. 導(dǎo)彈與航天運(yùn)載技術(shù), 1996(6): 52-59.

[3] 吳家駒, 榮克林. 多維振動(dòng)環(huán)境試驗(yàn)方法[J]. 導(dǎo)彈與航天運(yùn)載技術(shù), 2003(4): 27-32.

[4] 白鳳龍, 李宏男. 地震動(dòng)多點(diǎn)激勵(lì)下大跨空間網(wǎng)架結(jié)構(gòu)的反應(yīng)分析[J]. 工程力學(xué), 2010, 27(7): 67-73.

[5] 武芳文, 薛成鳳, 趙雷. 多維地震激勵(lì)作用下大跨度斜拉橋的隨機(jī)響應(yīng)[J]. 武漢理工大學(xué)學(xué)報(bào), 2010, 32(9): 344-347.

[6] 柳國(guó)環(huán), 李宏男, 田利. 九江長(zhǎng)江大橋在多點(diǎn)多維地震激勵(lì)下的反應(yīng)分析[J]. 振動(dòng)與沖擊, 2009, 28(9): 204-209.

[7] 陳穎, 田光明, 鐘繼根. 典型細(xì)長(zhǎng)體結(jié)構(gòu)的兩點(diǎn)激勵(lì)振動(dòng)試驗(yàn)設(shè)計(jì)[J]. 航天器環(huán)境工程, 2013, 30(1): 68-71.

[8] HAO H. Ground Motion Spatial Variation Effects on Circular Arch Response[J]. Journal of Engineering Mechanics, 1994, 120(11): 2326-2341.

[9] 趙懷耘, 田光明, 鐘繼根. 兩點(diǎn)激勵(lì)振動(dòng)試驗(yàn)時(shí)結(jié)構(gòu)模態(tài)對(duì)控制效果的影響分析[J]. 裝備環(huán)境工程, 2012, 9(6): 51-53.

[10] GEORGE A H, RICHARD S S, MARCOS A U. A Review of Multiaxis/Multiexciter Vibration Technology[J]. Sound and Vibration, 1996(4): 20-27.

[11] 王夢(mèng)魁. 多維振動(dòng)環(huán)境試驗(yàn)的實(shí)踐[J]. 裝備環(huán)境工程, 2005, 2(3): 23-25.

[12] 美國(guó)ANSYS公司北京辦事處. ANSYS動(dòng)力學(xué)分析指南[K]. 北京: 美國(guó)ANSYS公司北京辦事處, 2000.

Influences of Correlation Coefficient in Two-point Excitations

NONG Shao-ning, ZHAO Huai-yun

(Institute of Systems Engineering CAEP, Mianyang, 621900, China)

Objective The paper aims to derive the computational formula for random vibration response of structures under two-point excitations with spectrum function. Methods Response characteristics of the structural under two-point excitations were discussed with cross spectrum and correlation coefficient. Results For linear structures, the stimulated modal effects varied with different correlation coefficients under two-point excitations. With the increase of the correlation coefficient, the structural response spectrum increased and reduced alternately on adjacent resonance peaks. Conclusion Influences of structural vibration response character with different correlation coefficient should be worth of attention of the designers of engineering structures.

two-point excitation; correlation coefficient; random vibration

10.7643/ issn.1672-9242.2017.08.006

TJ01；O322

A

1672-9242(2017)08-0030-04

2017-04-05；

2017-04-25

NSAF基金項(xiàng)目(U1430129)

農(nóng)紹寧（1975—），男，廣西崇左人，碩士，高級(jí)工程師，主要研究方向?yàn)楣こ塘W(xué)。