基于仿真的動態環境試驗設備系統設計

牛寶良

基于仿真的動態環境試驗設備系統設計

牛寶良

（中國工程物理研究院總體工程研究所，四川 綿陽 621900）

目的 介紹計算機仿真技術的特點及其在動態設備系統設計中的應用。方法 首先簡要介紹仿真技術的發展和特點，其次介紹一些仿真經驗，最后通過若干實例介紹Simulink軟件在動態設備系統中的應用。結果 基于Simulink仿真，可以快速獲得系統運行過程中的各種所關注的參數運行結果，為系統性能評估和優化提供可靠的依據。結論 計算機仿真技術已經日趨成熟，應用于動態環境試驗系統設計中，可提升設計水平。

仿真；動態系統；代數環；環境試驗

環境試驗設備中，振動、沖擊、加速度、搖擺試驗設備等都屬于動態試驗設備。動態試驗設備系統的特性一般比較復雜，多個參數相互耦合，且往往是頻率的函數，這給系統的設計帶來困難。早期的設計技術只能采用簡化的基于解析公式的設計計算，以液壓振動臺的伺服閥為例，計算輸出流量時不考慮負載影響、或者負載按某個固定值來處理，而實際上，負載是時時刻刻都在變動中。伺服閥隨著頻率的增加，流量會衰減，相位滯后也會不斷增加，相位滯后對系統的穩定性也會有顯著影響。這樣一種處處簡化的設計手段，對系統動態特性的預估和了解是粗糙的、不全面的。因此也增加系統設計的風險。

仿真技術是分析動態系統的有效手段，它把各種相關的動態變量放到一組微分方程中，用模型（電路或者軟件）表達系統的動態特性，運行模型得到各量隨時間的變化曲線。后期隨著全數字仿真技術的發展，不僅僅是微分方程，各種非線性環節或者模塊也都可以進到系統模型中，因此逼真程度進一步提高。隨著微型計算機和仿真軟件的普及，仿真技術在各行各業應用越來越多。文中通過若干實例介紹仿真技術在動態環境試驗設備設計中的應用。

1 計算機仿真技術歷程與現狀簡介

仿真技術經歷了模擬計算機、數字模擬混合計算機、全數字計算機三個大的階段[1]。1946年，一臺能夠模擬導彈、飛機飛行軌跡等物理現象的模擬計算機在美國問世。標志著模擬仿真技術的開始。此后，涌現了大量的模擬機，20世紀50年代至60年代初是模擬計算機的黃金時期。盡管模擬仿真計算機取得了巨大的成功，但也暴露出數據精度不夠、實現插值函數困難、不能滿足數字控制系統的需要等問題。20世紀50年代末，由于導彈技術發展的需要，促使了混合仿真計算機的誕生。20世紀60年代至70年代中葉是混合仿真計算機的鼎盛時期。美國ADI公司1978年研制出全數字仿真計算機AD10，它的誕生標志著在那場混合仿真計算機與數字仿真計算機的激烈競爭中，全數字仿真計算機終領風騷，也標志著全數字仿真新時代的來臨。1973年美國研制成功專用液壓仿真軟件HYDSIM，之后歐美各國不斷發展完善液壓仿真軟件，1980年代先后推出了DSH（德國）、HASP（英國）等軟件。

1985年10月15日，我國第一臺全數字仿真計算機“銀河仿真I型計算機（YH-F1）”研制成功，標志著中國進入全數字仿真時代。此后又有多個新型的仿真計算機問世。

航空、航天是最先開始應用仿真技術的幾個傳統領域，是仿真計算機誕生的搖籃。也只有這樣的一些重要的、復雜的動態系統設計才用得起。

仿真技術的普遍應用則是在微型計算機普及和仿真軟件的圖形化編程之后，標志性的節點是MATLAB/Simulink仿真軟件的推出。MATLAB/Sim- ulink在仿真軟件中具有非常重要的地位。可以認為Simulink是一個分水嶺，之前建模是基于語句描述，模塊之間的關系靠語句定義，不能直觀看到系統的模塊組成和模塊之間的關系。Simulink提供了圖形化的建模方式，只要進行鼠標的簡單拖拉操作就可構造出復雜的仿真模型。它外表以方塊圖形式呈現，且采用分層結構。從建模角度講，這既適于自上而下（Top-down）的設計流程（概念、功能、系統、子系統、直至器件），又適于自下而上（Bottom-up）逆向程序設計。從分析研究角度講，這種Simulink模型不僅能讓用戶知道具體環節的動態細節，而且能讓用戶清晰地了解各器件、各子系統、各系統間的信息交換，掌握各部分之間的交互影響。這給建模帶來極大的方便，也有利于模型的查錯和修改。除了建模快捷方便外，其他功能也很強大，它可以處理的系統包括：線性、非線性系統；離散、連續及混合系統；單任務、多任務離散事件系統。 Simulink 6.5是里程碑版本，它的加速模式能使運算速度提高幾十上百倍。

除了MATLAB/Simulink外，還有一些仿真軟件，比如AMESim 是當今領先的傳動系統和液壓/機械系統建模、仿真及動力學分析軟件。再比如ADAMS，是應用較多的一種動力學仿真軟件。比如Modelica，是所謂的多領域建模軟件。它們各有特色，或者對某領域有特別的優勢，或者多學科綜合建模方面有優勢。

實時仿真系統也是仿真系統的一個重要分支，不僅要求獲得系統響應，而且要求響應與仿真對象實際的響應時間是嚴格的1:1。當具有這樣一種時間上的1:1特性時，就可以與真實的硬件系統連接，構成所謂的硬件在環仿真系統。這類系統通常都不是普通PC所能勝任的，需要專門的比較高端的硬件系統。國內外也都有相應的產品，國外產品有dSPACE，RT-LAB等，國內的有國防科技大學的KDRTS、西安二炮工程學院的CHY-Ⅲ、航天三院的海鷹實時仿真工作站、西北工業大學的并行計算機PD-100、北京華力創通科技有限公司的HRT1000、北京廣思特公司的半實物仿真系統、北京經緯恒潤科技有限公司的Higale半實物仿真系統等。

在環境試驗設備領域的仿真，應該說起步不算晚，李坦在1985年就在模擬計算機上開展了液壓振動臺的仿真[2]，但是由于仿真軟硬件等不成熟不方便等原因，并未大量普及。大約在2000年之后，仿真應用逐漸多了起來。2010年之后，特別是近幾年，進入了普遍應用階段[3—7,9—16]。

如今MATLAB/Simulink仍然是工程技術人員喜歡的仿真軟件之一。文中基于MATLAB/Simulink來介紹若干仿真實例，展示仿真給環境試驗設備設計帶來的便利。

2 仿真技術應用實例

2.1 仿真的幾個基本概念

2.1.1 連續與離散

以單自由度振動系統為例，它的運動方程是

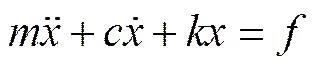
式中：為質量塊的質量，kg；為運動阻尼，N/(m·s－1)；為彈簧剛度，N/m；為質量塊的位移，m；為的二階導數，表示加速度，m/s2；為的一階導數，表示速度，m/s；為作用在質量塊上的力，N。

對應的拉氏變換的表達式為：

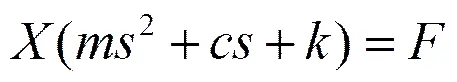
式中：是位移的拉氏變換；是力的拉氏變換。

式（2）對應的模型就是連續模型，它的Simulink模型可以用連續積分器1/構建，如圖1中的上面一個模型。把式（2）離散化（有多種離散辦法，應用較多的是Tustin變換），或者用連續積分器替代連續積分器1/s。這里用替換法，用梯形積分（Simulink還提供了前向積分、后向積分，都屬于矩形積分，精度比梯形積分差）替換連續積分，所得模型如圖1中下面一個模型。從模型形式上看，連續系統用的變量，離散系統用的變量。在內部解算上，連續系統有多種解算方法可選，而且這些算法一般都是變步長的多步算法，離散系統的算法則是定步長單步法。

采用離散系統建模有以下好處：離散系統支持Simulink的加速度模式，仿真速度快；單步法，運算量是固定的，仿真耗時也是固定的；半實物仿真系統必須是離散的，采用離散建模方便轉換到半實物仿真系統；記錄的響應數據是等間隔的，便于后續處理。文獻[11]給出了詳細實現方法。

當用離散積分器（梯形）替換完連續積分器1/之后，點擊運行，會提示“The model 'xxx' has an algebraic loop. Accelerator mode is not supported for models with algebraic loops.”，意思是模型有一個代數環，加速模式不支持代數環。

2.1.2 代數環

盡管離散系統有上述的好處，但是代數環是個問題。所謂的代數環，就是模型有環路（有反饋必然有環路），求解當前某個變量時，又要用到這個變量。對于動態系統，這幾乎是必然要遇到的。解決代數環有幾個辦法，最簡單的辦法是加延遲環節，或者積分器采用前向歐拉法（Forward Euler）。這些方法精度不高，有時還會發散。筆者提出了一個預測法，較好地解決了代數環。所謂的預測法，就是用前面若干點預測當前點的值。相應的Simulink模型見圖2和圖3。

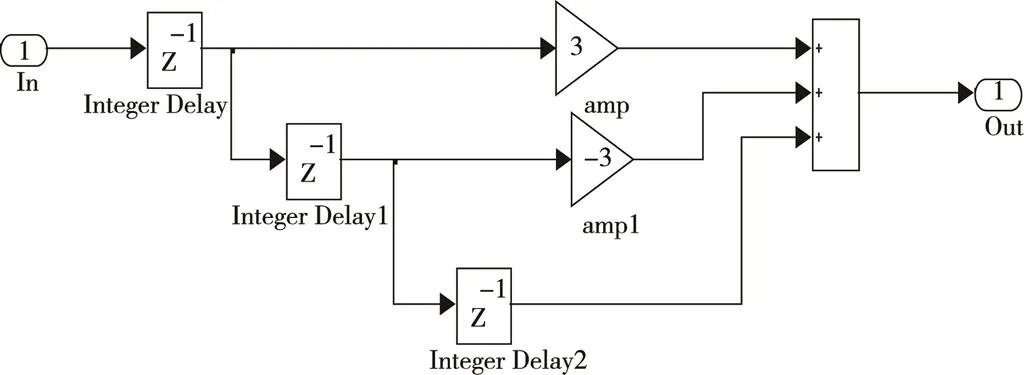
圖2 預測環節

注意：預測環節中有三個延遲器，如果知道初值，比如圖1所示的例子，加速度初值是一個重力加速度，就可以把它們的初值都置為9.806 65 m/s2；如果不知道初值，就置為0。帶來的后果就是仿真開始的幾個數據點不正確，之后就正確了，基本不影響仿真。

把這個模塊（模塊名pred）插入在mass1后面，見圖1下面的一個模型，代數環的問題就解決了。

對圖1所示的仿真模型，給定一組參數，＝10 kg，＝39478 N/m，＝125.66 N/( m·s－1)，可以仿真得到連續系統、離散系統的仿真結果，見圖4和圖5。可以看到，步長合適的情況下，連續系統、離散系統結果在采樣時刻是一致的，離散系統仿真結果波形是階梯狀的。這個模型同時也顯示了Simulink其實是可以在一個模型里同時有連續系統、離散系統。

2.1.3 采樣間隔

當采用離散建模時，采樣間隔是一個很關鍵的參數，采樣間隔的倒數是采樣頻率。一般來說，采樣頻率與系統中振蕩環節（也稱二階環節）的共振頻率相關。首先，為了能看清振蕩的響應，采樣頻率應該是振蕩環節的共振頻率的10倍以上。其次，為了仿真系統運行穩定（不發散），采樣間隔也應減小。越小的采樣間隔，一般精度越高，但同時仿真一次的耗時越長。因此，仿真間隔也是要從這兩方面取舍。通常可以先取1×10－4s或者1×10－5s，不行再調整。

2.1.4 上采樣、下采樣、抽取

一個物理系統，有時由快慢相差很大的模塊構成，這時如果采用統一的采樣間隔，那就只能確保快的模塊，即采樣間隔取小值。這樣一來，對于慢模塊來說，數據量就很大，許多數據是多余的，而且容易導致計算機內存溢出。

一種辦法就是采用抽取，即在示波器、數據保存模塊中，設置Sampling參數的Decimation,比如設置Decimation值為100，表示每運算100步，記錄1個數據到示波器、數組、或者文件中。這種辦法數據量可以減下來，但是模型計算量一點不減少。

另一種辦法是采用上采樣、下采樣的辦法。即慢速模塊用一個比較大的步長，而快的模塊用一個小的步長，慢模塊的輸出進到快模塊前用上采樣（Upsample），快模塊的輸出進到慢模塊前用下采樣（Downsample）。Upsample、Downsample在Signal Processing Blockset下的Signal Operations目錄下可以找到。下采樣模塊直接使用沒有問題。上采樣模塊不能直接使用，因為它是采用加0的辦法提高采樣頻率，把一個連續的信號變成了脈沖信號，如圖5的上圖所示。筆者給出了修正的上采樣模塊，如圖3所示，得到的上采樣后的波形如圖5的下圖所示。這樣，慢模塊的運算量的減小了很多，整個系統的仿真速度就能大幅提高。

總之，適當設置抽取參數、采用上采樣、下采樣有利于避免內存溢出，有利于減小數據、方便后續處理和顯示，有利于提高仿真速度。抽取的原則是信號的每個周期有10～100個數據點為佳。點數再少波形就太粗糙，點數再多也沒有太大意義。對于掃頻信號，只能按最高頻率來設置。

避免內存溢出的另一個辦法是在示波器上勾選（limit data points to last）選項，填寫數據點數，只保留仿真最后的若干數據點。把數據寫入文件既能把全程數據保留下來，也不會導致內存溢出。

2.1.5 單位

單位其實很重要。由于歷史原因，各種非國際單位制的單位仍沒有完全淘汰，再者，有些單位比較直觀方便，仍在使用。筆者的觀點是方便的或者習慣的單位可以用，但是進入仿真程序時一律換算為國際單位制，仿真結果用于顯示時，可以再換算為日常習慣的單位。比如加速度，通常習慣用作單位，仿真時必須換算為m/s2，流量用L/min，仿真時必須換算為m3/s。有些弄簡成繁的單位，比如質量用kg·ｓ2/cm，則應堅決淘汰。單位正確是仿真結果正確的重要保證。

2.2 液壓振動臺

液壓振動臺在裝備環境試驗、汽車道路模擬試驗、地震模擬試驗等方面廣泛應用。雖然技術指標有所不同，但是主要構成、控制原理是相同的。下面以某10 t振動臺為例介紹仿真的應用，結構如圖6所示。主要參數：位移為±120 mm，速度為1 m/s，加速度為10，負載為1 t。

液壓振動臺設計最主要的參數就是活塞有效面積，傳統的設計是基于最佳功率匹配原則[8]，或者簡單的負載壓強＝2/3油源壓強。基于仿真的設計，可以以2/3原則計算初值，通過仿真全面了解在整個頻帶上的效果，然后再進行迭代。液壓臺的流量也是系統的主要參數之一。有文獻分析過，共振頻率處最低，超過共振頻率后，逐步上升。通過仿真可以了解全頻帶的流量需求。建立的液壓振動臺Simulink模型如圖7所示。

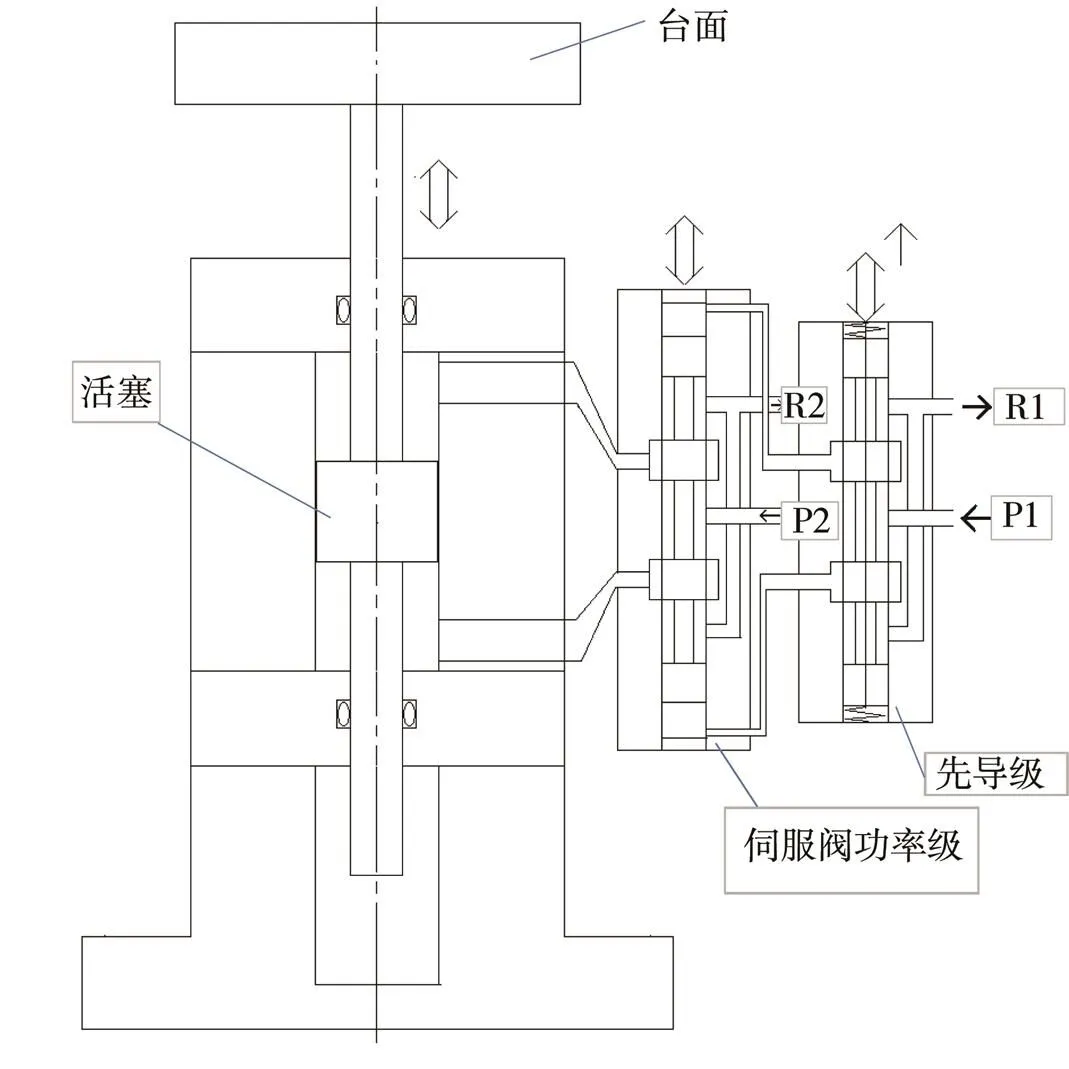
圖6 液壓振動臺結構

利用該仿真模型可以仿真研究[9]：理想情況下的性能；活塞摩擦對波形的影響；基礎質量對波形的影響；控制算法對性能的影響；伺服閥遮蓋對波形的影響；負載振動頻率特性；基礎的振動響應。

這里僅介紹兩種三狀態控制仿真情況。一種是電壓輸入，一種是加速度輸入。

電壓輸入時，希望最大電壓在不同頻率對應不同的量的最大值，低頻10 V對應最大位移，中頻段，10 V對應最大速度，高頻段，10 V對應最大加速度。這樣既能發揮振動臺的最大能力，也不會因為飽和削波導致波形失真。優化后的效果見圖8。

另外一種是加速度輸入，給定的輸入信號與目標加速度信號成比例，控制器優化的目標是讓響應加速度盡可能逼近給定加速度。從傳函來說，希望傳遞函數接近一根平直的直線。優化后的某地震波控制如圖9所示。由于低頻段受位移限制，加速度很小，所以采用加速度輸入進行地震波試驗時，必須先做一次三參量生成，看看位移、速度是否超振動臺極限，確認不超極限時，方可進行試驗。

2.3 二維搖擺試驗機

二維搖擺試驗機是中國工程物理研究院總體工程研究所研制的一套試驗系統。在研制階段進行了仿真分析，其結構和仿真模型如圖10和11所示。

系統主要參數：運動自由度為兩自由度，即可同時進行橫搖和縱搖；最大負載質量不小于1 000 kg；負載高度極限不低于2 200 mm；臺面尺寸不小于 2 200 mm×2 200 mm；負載質心高度極限不低于1 000 mm；傾斜試驗能力，最大橫傾角為±45°，最大縱傾角為±30°；搖擺試驗能力，最大橫搖角為±60°、橫搖周期為3～14 s，最大縱搖角為±30°、縱搖周期為4～10 s；傾斜搖擺復合試驗能力（配30°傾斜夾具），最大橫搖角為±60°、橫搖周期為3～14 s，最大縱搖角為±15°、縱搖周期為4～8 s；

通過仿真，得到如圖12所示的閥流量、角位移，得到圖13所示的負載角速度、驅動力矩、機械功率，以及其他關注量，比如跟蹤誤差、齒隙對搖擺角度影響等。對閥選型、供電功率配置等提供了有力支撐。

2.4 離心機

中國工程物理研究院總體工程研究所2號離心機，容量為200t，最大離心加速度為200。系統結構主體見圖14。系統的仿真模型見圖15。細節可參考文獻[10—12]。

通過仿真，可以確定多大的上升速率可行，或者給定的一個上升速率，需要的多大電壓、電流。如圖16所示。也可以為新離心機設計提供支撐。

2.5 游戲機

某升降游戲機的結構如圖17所示。負載為4 000 kg，最大升程為20 m，通過滑輪組實現3倍的位移放大。負載通過兩根鋼絲繩提升，相當于每根鋼絲繩承受0.5倍載荷。

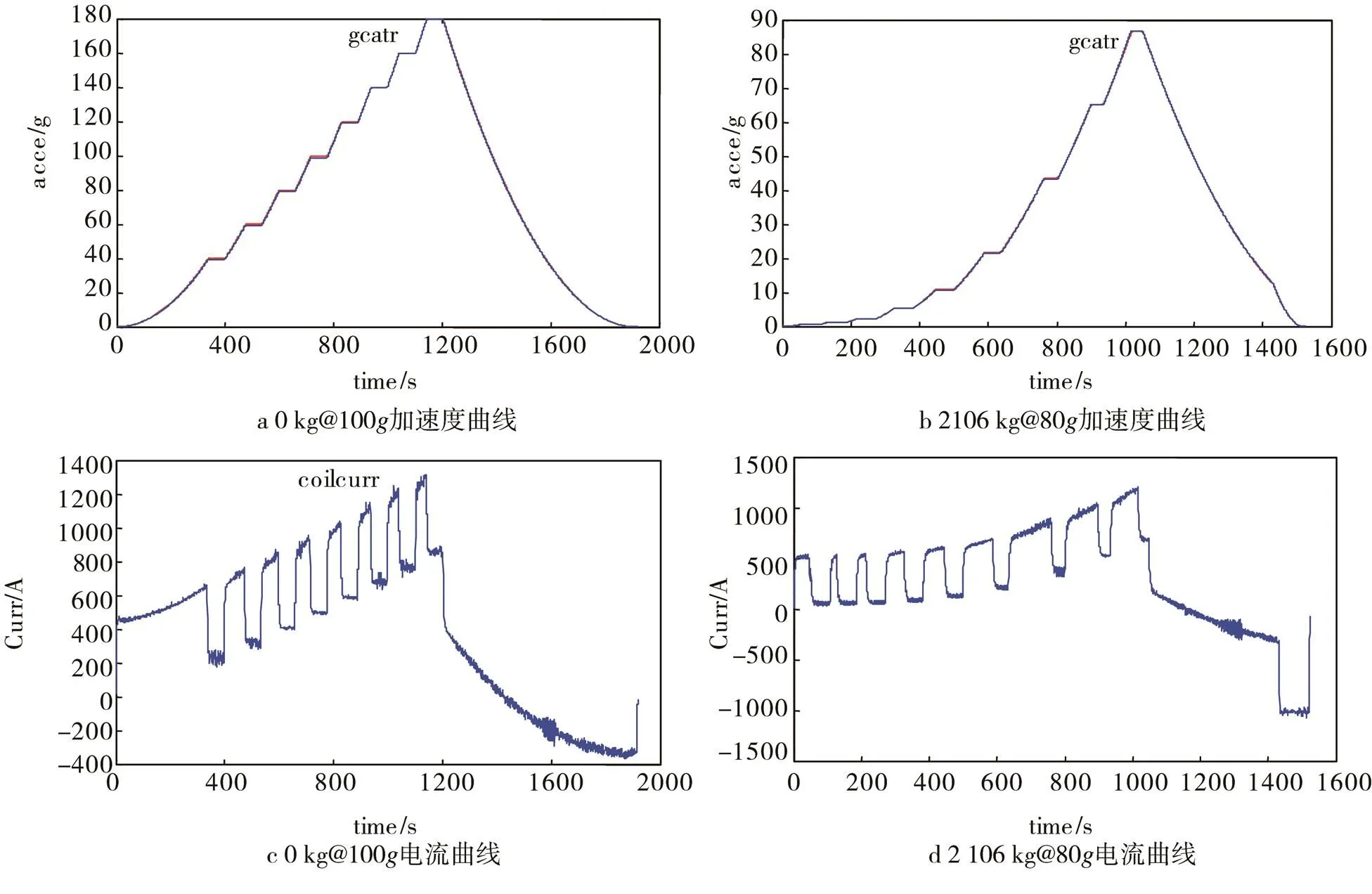
圖16 加速度、電流時域曲線

系統仿真模型如圖18所示。包括信號源、控制器、伺服閥、振動系統等幾個模塊。控制器采用PIDF控制算法。伺服閥采用雙出口伺服閥模型，液壓缸采用單出桿模型，可真實反映上下兩腔的油液壓強及液壓缸的輸出力。振動部分用鋼絲繩把液壓缸活塞和負載連接，鋼絲繩用單邊剛度彈簧表示，只承受拉，不承受壓，壓剛度為0。現通過仿真設計系統的主要參數，比如可實現的加速度、液壓伺服閥的流量、液壓缸的缸徑桿徑、油源的壓力、流量、一次升降需要的油液等。

通過多次迭代優化，確定伺服閥額定流量為800 L/min，油源壓力為21 MPa、流量為600 L/min。負載運動的位移、加速度見圖19。

可以看到，負載較好跟蹤了給定位移，有三個時刻達到失重（－1加速度），鋼絲繩峰值載荷為81.26 kN。作為游戲機，主要是給游客加速度感覺，這樣的結果是滿意的。如果是作為工業控制，需要精確跟隨給定位移，有若干辦法來提高精度，比如增加活塞面積、改變鋼絲繩剛度、嘗試不同的控制策略和控制參數等。

3 對仿真的再認識

仿真技術的作用已經無需質疑，對于復雜系統，通過仿真可以提高設計效率和質量，節約研制經費。在此，簡要總結一下對仿真的幾點認識。

1）深化對系統的認識。仿真模型的建立依賴一定的科學規律，而這些科學規律往往是理想條件下對單一問題的科學表述，比如牛頓第二定律=，黏性阻尼力=·，彈性定律=。一個單自由度系統，包含了上述三個規律，理想情況下可以得到解析式。如果阻尼力是=·v，或彈簧力=kx，或彈簧是鋼絲繩類（受拉有剛度，受壓剛度為0），或很多的自由度，解析表達式就可能得不到，因而也就不能得到其響應和認識其規律。這些對于仿真來說，則是非常容易的。因此，科學規律是建模的基礎，而建模與仿真可以獲得對系統更深入全面的認識。

2）系統參數設計與優化。當給定一組設計目標參數后，基于建模仿真，就可以得出系統相關的許多參數，比如液壓振動臺設計，通過仿真可以得到基礎質量、油源壓力、電源功率等一系列外界供給參數，由此分析系統的建造規模、經費等。通過多輪次迭代，可以進行優化，以最低的成本獲得最大收益。

3）控制器設計與優化。含有控制系統的試驗系統，其控制系統往往成為系統的核心子系統，它的算法決定了系統的穩定性（穩定余度）、控制精度等。在仿真系統不用擔心系統不穩定導致的設備損壞；可以施加多種不同的載荷，檢查控制算法的適宜性；算法、控制器參數、被控對象等的修改只需修改仿真模型，操作快速。整個過程安全、便捷、高效。

4）故障與異常分析。對于真實的系統，人為制造某種故障檢查系統的反映是有很大風險的，在仿真系統中，則不存在任何風險。可以安全、方便地觀察系統的反應、故障聯鎖機制是否起效。

5）人員培訓。比較操作復雜的重要系統，比如飛機駕駛、高鐵駕駛、核電站的操作，采用仿真機進行培訓，是安全、高效、節約的培訓方式。

6）分析工程因素的影響。在做系統設計時，往往用的理想模型。比如伺服閥，理想情況是零遮蓋。實際四個節流邊的遮蓋量肯定是非零的，且不相同。可以建立雙出口四邊滑閥模型，人為給定不同的正負遮蓋量，通過仿真看看它們對系統波形失真、控制精度等的影響。再比如摩擦力，分析原理時往往不考慮摩擦或者給一個固定的摩擦力值，實際上與加工間隙或過盈量、密封件的材質、壓縮量等都有關系，可以人為給一些不同的摩擦力，看看對系統性能的影響，或找到摩擦力允許的上限值。

7）仿真的“真”與“不真”。在正確建模的情況下，可以說仿真得到的規律是“真”的，仿真的值是“不真”的。因為如果模型正確，仿真結果就能反映系統主要運行規律。如果模型不正確，規律也就不正確了。

以液壓振動臺為例，用二階振蕩環節表示一個伺服閥時，振動波形不失真，與實際系統相差甚遠。因為模型已經忽略了閥壓降這樣一個顯著的非線性因素。加上閥壓降這個非線性因素，則振動波形失真特性就能顯示出來。再以摩擦為例，不考慮摩擦，則波形光滑不失真。加上摩擦這個實際存在的因素，結果就與實際相近，如圖20所示。

實際的系統是非常復雜的，常常不愿或者不能建立反映每個參數細節的模型。以液壓缸的摩擦為例，具體每個液壓缸的摩擦力都是不一樣的（每個液壓缸的密封圈槽尺寸有加工誤差、每個密封圈有加工誤差、運行溫度也會影響密封圈的壓縮量）。再以油液粘度為例，它是溫度、壓力的函數，建模時也常常把它當作常數，也會帶來誤差。伺服閥的頻率特性每一臺各有不同，即使是同一臺，它的頻率特性與流量幅值還有關系，小流量頻響范圍寬，大流量頻響范圍小等。這些因素導致仿真輸入參數與實際存在差異，因此仿真的值是“不真”的，但是這個所謂的不真，是有限度的，不能因此而否定仿真。

總之仿真可以反映系統的主要、基本的規律，得到的結果具體值與實際系統會有差異，認識這點，才能正確看待仿真技術。

4 結語

文中簡略回顧了仿真技術的仿真歷程，給出了一些經驗和若干仿真在環境試驗設備方面的應用實例，總結了仿真技術的認識。從中可以看出，計算機仿真技術在環境試驗設備研制中大有作為，將來伴隨著仿真技術的發展，環境試驗設備研制也會越來越快速、準確。

[1] 李興瑋, 曹娟. 仿真計算機的過去?現在和未來[J]. 系統仿真學報, 2009,21(S2): 106-111.

[2] 李坦. 位移及加速度控制的液壓伺服振動合的動態優化設計[J]. 試驗機與材料試驗, 1985(2): 15-22.

[3] 李長安, 王長江, 何長安. 不對稱結構的防滑剎車壓力伺服閥的仿真研究[C]// 97中國航空學會液壓與氣動專業學術討論會. 1997.

[4] 吳志清. 四通閥控非對稱液壓缸伺服系統的動態特性[J]. 煤礦機械, 2004(7): 32-34.

[5] 江桂云, 王勇勤, 嚴興春. 液壓伺服閥控缸動態特性數學建模及仿真分析[J]. 四川大學學報(工程科學版), 2008(5): 195-198.

[6] 任杉, 李瑋, 韓青. 基于MATLAB 的閥控缸伺服系統仿真分析[J]. 裝備制造技術, 2009(9): 32-33.

[7] 徐敏, 薛敏東, 王曦. 噴嘴擋板式力反饋電液伺服閥非線性動態模型[C]// 2010年中國國防科技會議. 西安, 2010.

[8] 關景泰. 機電液控制技術[M]. 上海: 同濟大學出版社, 2003.

[9] 牛寶良, 王玨. 液壓振動臺時域建模與仿真[J]. 裝備環境工程, 2010, 7(6): 247-251.

[10] 鈕王杰, 張斌超, 劉春艷. 基于MATLAB/Simulink轉速閉環直流調速控制系統的仿真研究[J]. 山西大同大學學報(自然科學版), 2011, 27(5): 33-35.

[11] 牛寶良. 一種計算結構時程響應的簡單直接積分法[C]// 第23屆全國結構工程學術會議. 蘭州,2014.

[12] 牛寶良. 某離心機模型辨識與仿真[J]. 裝備環境工程, 2015, 12(5): 61-66.

[13] 劉增光, 岳大靈, 安林超, 等. 基于MATLAB 的力反饋兩級電液伺服閥建模與仿真[J]. 液壓與氣動, 2015(5): 83-85.

[14] 張宏, 高銘, 郭凱. 伺服閥開口度對電液伺服系統動態特性的影響[J]. 液壓氣動與密封, 2015(10): 27-30.

[15] 張軍, 左哲清, 王書銘. 數字伺服閥卡滯問題研究[J]. 液壓與氣動, 2014(6): 105-107.

[16] 沈偉, 崔霞. 比例伺服閥靜動態特性仿真建模[J]. 計算機仿真, 2015, 32(2): 236-240.

Dynamic Environment Test Equipment System Design Based on Simulating

NIU Bao-liang

(Institute of System Engineering, China Academy of Engineering Physics, Mianyang 621900, China)

ObjectiveTo introduce characteristics of simulation technology and its application in designing dynamic equipment system. Methods Development, characteristics and experience of simulation technology were introduced firstly. Application of Simulink software in dynamic equipment system was introduced with several examples. Results Main characteristic parameters concerned could be obtained quickly with Simulink simulation. It gave dependable data to evaluate or optimize the equipment system. Conclusion The computer simulation technology is quite mature and can be used in the dynamic environment test system design to advance the design level.

simulation; equipment; dynamic system; algebraic loops; environmental test

10.7643/ issn.1672-9242.2017.08.001

TJ01；TB114

A

1672-9242(2017)08-0001-10

2017-04-18；

2017-05-15

牛寶良 (1963—)，男，陜西人，碩士，研究員，主要從事振動、離心試驗及相關設備研發。