基于校驗和更新的低復雜度LDPC碼硬判決譯碼算法

吳伊蒙,石志東,鄧斌

(上海大學通信與信息工程學院,上海200444)

基于校驗和更新的低復雜度LDPC碼硬判決譯碼算法

吳伊蒙,石志東,鄧斌

(上海大學通信與信息工程學院,上海200444)

為使低密度奇偶校驗(low-density parity-check,LDPC)碼的硬判決譯碼算法具有更低的計算復雜度和更高的譯碼性能,提出了一種新的校驗和計算算法,具有較低的計算量,可應用于現有的所有硬判決譯碼算法.結合該算法對一種計算量近似于比特翻轉(bit fl ipping, BF)算法的多閾值比特翻轉(multi-threshold BF,MTBF)算法進行了進一步改進,獲得了更低的譯碼復雜度和更好的譯碼性能,在迭代5次時獲得了0.15 dB的性能增益.

低密度奇偶校驗碼;硬判決譯碼;低復雜度;校驗和更新;多閾值比特翻轉

低密度奇偶校驗(low-density parity-check,LDPC)碼最早由Gallager[1]于1962年提出,歷經數年發展,其譯碼算法主要已發展為硬判決譯碼和軟判決譯碼兩大類.設計良好的軟判決算法具有非常優異的譯碼性能,但譯碼復雜度也隨之上升.硬判決算法雖然譯碼性能較差,但其具有遠低于軟判決算法的譯碼復雜度,非常適用于一些資源配置都很有限的網絡環境(如WSN,Ad hoc網絡等),該優勢是軟判決算法所不可比擬的.因此,為了進一步發揮硬判決算法的優勢,現有的硬判決算法大多致力于譯碼性能的提升和譯碼復雜度的降低,使硬判決算法具有更廣闊的應用空間.

最早的硬判決算法是由Gallager提出的比特翻轉(bit fl ipping,BF)算法[1].該算法僅依靠校驗信息計算作為判決條件,可在單次迭代中翻轉多個比特,計算量非常低,但是性能也較差. Kou等[2]提出的加權BF(weight BF,W BF)算法,在判決條件計算中引入了比特的幅值信息,而且在單次迭代中只翻轉一個比特,使得比特翻轉更加可靠.之后的改進型WBF(modified WBF,MWBF)[3]以及改進的MWBF(improved MWBF,IMWBF)[4]等算法又在WBF算法的基礎上做了進一步改進,將BF算法的性能進行了進一步的提升.但是由于判決條件的計算引入了新的計算量,而且其單次迭代只翻轉一個比特,使得該類算法的計算量不可避免地增加.為了降低其計算復雜度,各種多比特翻轉算法被提出,如梯度下降BF(gradient descent BF, GDBF)算法[5]、自適應加權多比特翻轉(adaptive weight multi-BF,AWMBF)算法[6].這些算法通過在單次迭代中翻轉多個比特減少計算復雜度,但是譯碼性能也不可避免地受到影響,多要以計算更為復雜的判決條件來補償,從而取得更好的譯碼性能.而文獻[7]提出的多閾值比特翻轉(multi-threshold BF,MTBF)算法,通過設置多個閾值可在單次迭代中翻轉多個比特,具有近似于標準BF算法的譯碼復雜度和更快的收斂速度,但是較之AWMBF算法及一些混合類算法[8-9],其譯碼性能仍有些微差距.

為了獲取譯碼復雜度更低、性能更好的硬判決算法,本工作提出了一種新的校驗和更新算法,對校驗和計算進行了簡化,使硬判決譯碼算法具有更低的計算復雜度,并結合所提出算法對MTBF算法進行了改進,在降低其計算復雜度的同時還獲得了譯碼性能的提升.

1 校驗和更新算法

首先,令規則二進制LDPC碼的校驗矩陣為H,它是一個M×N的稀疏矩陣,每列含有γ個“1”,每行含有ρ個“1”,比特n參與的校驗方程的集合為M(n)={m:hmn=1}.c=[c1, c2,···,cN-1]為編碼后的碼字,x=[x1,x2,···,xN-1]為二進制相移鍵控(binary phase shift keying,BPSK)調制后的碼字,經加性高斯白噪聲(additive white Gaussian noise,AWGN)信道傳輸后的接收信息為r=[r0,r1,···,rN-1],其中rn=xn+vn,vn為高斯隨機變量,均值為0,方差為σ2=N0/2.對r進行硬判決后得到z=[z0,z1,···,zN-1],校驗和s=

由于在硬判決算法的每次迭代中都需對校驗和s=zHT進行計算,而該過程需采用一個1×N矩陣與一個N×M矩陣的乘積,因此經過多次迭代后將耗費非常大的計算量,尤其在碼長較長時其計算量將更大.由于硬判決譯碼的校驗和計算均采用模二加法運算,所以碼字的每次翻轉都會引起其對應的γ個校驗方程的改變.基于此,本工作提出了一種新的校驗和更新算法,只在譯碼運算中進行一次校驗和計算,其后的每次迭代只需在碼字翻轉時直接翻轉其對應的γ個校驗和,而不再進行s=zHT運算.如圖1所示,對于列重為2的校驗矩陣H,當比特z0翻轉時,z0所參與的兩個校驗方程s0,s1的計算結果也發生改變,由0變為1,或由1變為0,因此只需在每次比特翻轉后翻轉其對應的γ個校驗和即可,而無需對所有的校驗方程進行計算.校驗和更新的計算過程可總結如下.

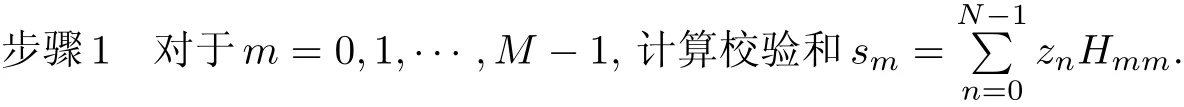
圖1 校驗和更新原理Fig.1 Principle of check-sums updating

步驟3計算翻轉條件(本步驟可代入各種硬判決算法),翻轉相應比特zn,同時更新zn所對應的γ個校驗和,將其由0翻轉為1或由1翻轉為0(對sm取非,即sm=!sm,m∈M(n)).

步驟4重復步驟2和步驟3,直到滿足所有的校驗和或達到最大迭代次數.

對于上述算法,本工作選用了文獻[7]中的MTBF算法進行驗證,校驗矩陣采用碼長為1 023、列重和行重均為32的歐氏幾何矩陣,其仿真圖形如圖2所示,其中BER(bit error ratio)為誤碼率,ITE(iteration)為迭代次數.MTBF算法采用的是普通的校驗和算法進行計算,而New-MTBF算法是本工作提出的校驗和更新算法.由圖中可以看出,MTBF算法在采用兩種校驗和計算方法時的譯碼性能完全一致,說明本工作提出的更新算法可以替代普通的校驗和計算算法,且不會對譯碼算法的性能產生影響.

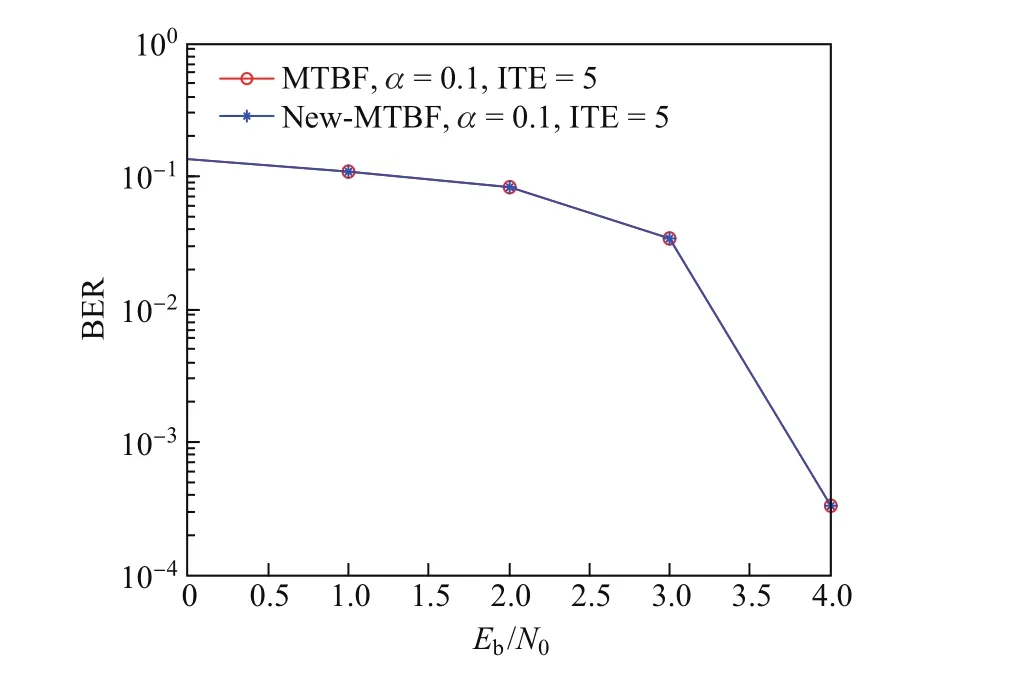
圖2 MTBF和New-MTBF算法的譯碼性能比較F ig.2 Performance comparisons decoded by MTBF and New-MTBF algorithms

在本算法中,每次譯碼只需進行一次校驗和計算,其后的每次迭代也只需進行32x (γ=32)次邏輯運算即可完成校驗和計算,其中x為每次迭代時翻轉的比特數目,且隨著信噪比(signal to noise ratio,SNR)的增大,每次迭代所翻轉的比特數目會逐漸減少,計算量也會隨之變小.尤其對于一些單次迭代只翻轉1個或少數幾個比特的譯碼算法,可以有效降低其計算復雜度,而且碼長越長、迭代次數越多、單次迭代中翻轉的比特數目越少,相應的減少的計算量也越多.此外,本算法在校驗和計算中不必調用整個校驗矩陣,可減少對存儲的訪問,在硬件實現中具有更低的解碼時延.本校驗和更新算法最大的優勢在于其具有很強的適用性,可以適用于各種硬判決算法.

2 改進的MTBF算法

文獻[7]中提出的MTBF算法與大數邏輯算法[10]較為類似.由于接收信息rn的幅值為浮點小數,大數邏輯算法在譯碼的初始化階段將浮點小數化為整數進行運算,從而減少了譯碼迭代中的運算量.MTBF算法采用類似的方法,根據其幅值的大小設定多個閾值,在譯碼運算中不再進行浮點小數計算,單次譯碼迭代中可翻轉多個比特,有效減少了譯碼的迭代次數,并且譯碼性能也超過了常見的WBF[2]和IMWBF[4]等算法的性能,使得MTBF算法以較低的譯碼復雜度獲取了較高的譯碼性能.但是由于MTBF算法只簡單依靠校驗和信息以及碼字的幅值信息進行碼字的翻轉,使得碼字翻轉的可靠度較之譯碼復雜度較高的AWMBF[6]等算法相對較低,因而本工作對MTBF算法做出了一些改進,增加了一些新的判決信息來提升比特翻轉的可靠度,提高譯碼性能,同時引入了第1節中提出的校驗和更新算法,以降低譯碼復雜度.

首先,對于接收信息rn=xn+vn,其中xn為BPSK調制后的碼字,其值為“+1”或“-1”, vn為高斯隨機變量,此時|rn|越大則該比特就越可靠.由于該變化由vn引起,那么若vn引起|rn|發生正的變化(|rn|>1),則rn就越可靠;若發生負的變化(|rn|<1),則rn就越不可靠.因此,本工作采用了噪聲信號的不可靠度en=1-|rn|來衡量硬判決算法中的比特不可靠度,若en越小,則該比特越可靠.較之于MTBF算法,本工作在改進算法中對閾值組數不再嚴格控制為?γ/2」組,而是由參數α決定,使得閾值選擇更加靈活;而當en<0時,閾值則統一被設定為Tn=2×?γ/2」-2.同時,為了增加比特翻轉的準確性,本工作在每個符合翻轉條件的比特zn及其所對應的校驗和都翻轉后,會計算此時zn不滿足的校驗方程翻轉前所不滿足的校驗方程數目,如果g>f,說明該nn次翻轉不成功,將zn及其對應的校驗和重新翻轉回去,反之則翻轉成功,繼續譯碼.改進后的MTBF(improved MTBF,IMTBF)算法步驟如下.

步驟1計算比特的不可靠度en=1-|rn|,n=0,1,···,N-1,使用預定參數α (α>0)將其分為多個群組.如果en>0,對于(k-1)α<|en|≤kα(k為大于0的正整數),閾值被設置為Tn=2×?γ/2」-k;如果en≤0,則Tn=2×?γ/2」-2.對于m=0,1,···,M-1,計算校驗和

步驟4重復步驟2和步驟3,直到滿足所有的校驗和或達到最大迭代次數.

3 仿真結果及性能分析

本工作采用MATLAB對上述算法進行仿真,校驗矩陣采用歐式幾何法構造,大小為1 023×781,碼長為1 023,校驗矩陣的列重和行重均為32,其仿真圖形如圖3～5所示.

圖3為IMTBF算法在不同的信噪比下BER隨參數α的變化曲線.可以看出,本工作提出的IMTBF算法在信噪比較高時受α的影響較大,但在不同的信噪比下BER隨α的變化較為一致,因而本工作選取α=0.05.

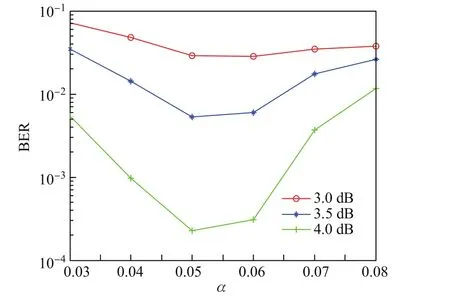
圖3(1 023,781)EG-LDPC碼在IMTBF算法下采用不同的α值時的譯碼性能Fig.3(1 023,781)EG-LDPC codes’performance comparisons decoded by IMTBF algorithmwith diff erent values ofα

圖4 為BF,MTBF和IMTBF算法在不同信噪比下迭代5次時的性能仿真比較,其中, MTBF算法選取的α值為0.10.可以看出,改進后的算法較之改進前在迭代次數為5時有明顯的性能提升,在BER為10-5時獲得了約0.15 dB的性能增益,而BF算法在迭代5次時,其譯碼性能卻與MTBF和IMTBF算法有較大差距,說明改進后的譯碼算法也有較快的收斂速度,能夠以較少的迭代次數換取較高的譯碼性能.

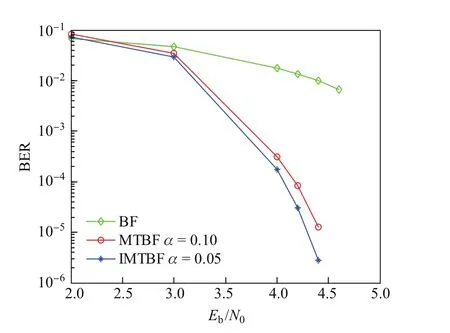
圖4 (1 023,781)EG-LDPC碼采用BF,MTBF和IMTBF算法在不同信噪比下的性能比較Fig.4(1 023,781)EG-LDPC codes’performance comparisons decoded by BF,MTBF and IMTBF algorithms with diff erent SNR

此外,從IMTBF與MTBF算法的描述中分析可知,二者的譯碼復雜度大致相似,主要差別在于二者的步驟3中gn及校驗和的計算.在IMTBF算法中由于每翻轉一個碼字zn都要計算其不滿足的校驗方程的數目需采用一個1×1 023矩陣乘以一個1 023×1矩陣.若IMTBF算法在單次迭代中需翻轉x個碼字,則IMTBF算法需多計算一個1×1023矩陣乘以1 023×x矩陣,該過程需進行1 022x次加法和1 023x次乘法.此外,IMTBF算法在迭代中無需計算校驗和,只需32x次邏輯操作即可.而MTBF算法中校驗和的計算則需一個1×1 023矩陣乘以一個1 023×1 023矩陣,同理需要約106次加法和106次乘法.由于x必定小于1 023(2≤SNR≤3時,x通常小于300,SNR≥4時,x通常小于90或更小),所以IMTBF算法的譯碼復雜度理論上低于MTBF算法.而且IMTBF算法的譯碼復雜度與x有關,那么隨著信噪比的增大,翻轉比特的數目會逐漸減少,此時IMTBF算法的計算量也會隨之減少.本工作對兩種算法的加法和乘法復雜度進行了仿真計算,如圖5所示.仿真結果表明,IMTBF算法的加法和乘法計算量均低于MTBF算法,且隨著信噪比的增大,兩種算法的計算量均逐漸減少,但IMTBF算法的計算量始終低于MTBF算法.

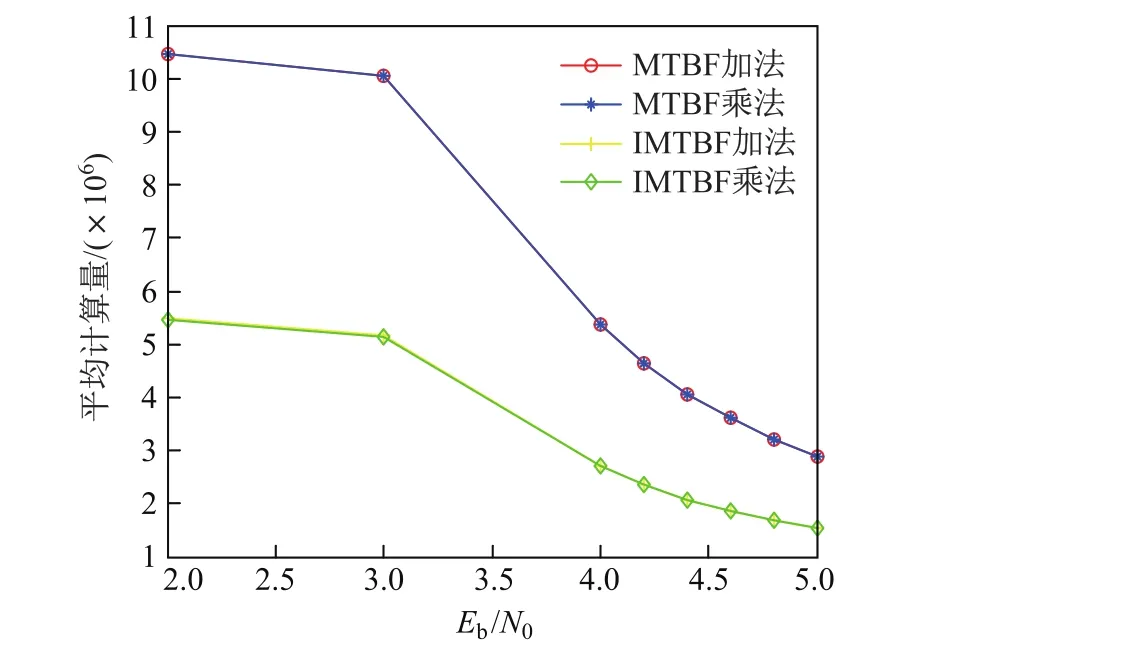
圖5 MTBF和IMTBF算法在不同信噪比下的計算量比較Fig.5 Computations comparisons of MTBF and IMTBF algorithmswith diff erent SNR

4 結束語

本工作提出了一種新的校驗和更新算法,可以有效減少校驗和計算過程中的計算量,且不會對算法的譯碼性能造成影響,能夠降低譯碼過程中的譯碼時延,因而可適用于現有的各種硬判決譯碼算法及一些軟判決譯碼算法.此外,本工作結合所提出算法對MTBF算法進行了改進,采用了噪聲信號的不可靠度作為硬判決算法中比特不可靠度的衡量,使閾值選擇更加靈活,并引入了新的判決信息來增加比特翻轉的可靠度.仿真結果表明,改進后的IMTBF算法具有更低的譯碼復雜度和更好的譯碼性能,在BER為10-5時,迭代5次后獲得了0.15 dB的性能增益.

[1]G ALLAGER R G.Low-density parity-check codes[J].Information Theory,1962,8(1):21-28.

[2]K OU Y,L IN S,F OSSORIER M.Low-density parity-check codes based on finite geometries:a rediscovery and new results[J].Information Theory,2001,47(7):2711-2736.

[3]Z HANG J,F OSSORIER MP C.Amodified weighted bit-fl ipping decoding of low-density paritycheck codes[J].Communications Letters,2004,8(3):165-167.

[4]J IANG M,Z HAO C,S HI Z,et al.An improvement on themodified weighted bit fl ipping decoding algorithmfor LDPC codes[J].Communications Letters,2005,9(9):814-816.

[5]W ADAYAMAT,N AKAMURAK,Y AGITAM,et al.G radient descent bit fl ipping algorithms for decoding LDPC codes[J].Communications,2010,58(6):1610-1614.

[6]C HEN T C.Adaptive-weightedmu ltibit-fl ipping decoding of low density parity-check codesbased on ordered statistics[J].IET Communications,2013,7(14):1517-1521.

[7]L IU Y H,N IU X L,Z HANG ML.Multi-threshold bit fl ipping algorithmfor decoding structured LDPC codes[J].Communications Letters,2015,19(2):127-130.

[8]T ORSHIZI E O,S HARIFI H,S EYRAFI M.Anew hybrid decoding algorithmfor LDPC codes based on the improved variab lemultiweighted bit-fl ipping and BP algorithms[C]//2013 21st Iranian Conference on Electrical Engineering.2013:1-6.

[9]T ORSHIZI E O,S HARIFI h,D ANESHGAR A,et al.Anew hybrid decoding algorithmbased on multi-dimensional searching for regu lar LDPC codes in finite geometries[C]//2014 22nd Iranian Conference on Electrical Engineering.2014:1471-1476.

[10]L IN S,C OSTELLO D J.Error control coding:fundamentals and applications[J].Prentice-Hall Computer Applications in E lectrical Engineering Series,1983,25(1):4-12.

H ard-decision decod ing algorithmwith low complexity based on check-sumupdating for LDPC codes

WU Yimeng,SHIZhidong,DENG Bin
(School of Communication and In formation Engineering,Shanghai University,Shanghai 200444,China)

To reduce computational complexity of hard-decision decoding algorithms of low-density parity-check(LDPC)codes and improve decoding performance,a check-sums algorithmis proposed.It requires less computation,and is applicable to all existing harddecision algorithms.The algorithmis applied to a multi-threshold bit fl ipping(MTBF) algorithmwhose computation complexity is similar to the bit fl ipping(BF)algorithm,and further improvement ismade.The resu lts show that the proposed algorithmcan achieve a 0.15 dB performance gain after 5 iterationswith lower computational complexity and better decoding performance.

low-density parity-check(LDPC)codes;hard-decision decoding;low complexity;check-sums updating;multi-threshold bit fl ipping(MTBF)

TN 919.3+2

A

1007-2861(2017)04-0510-07

DO I:10.12066/j.issn.1007-2861.1674

2015-09-28

國家自然科學基金資助項目(11474195);上海市自然科學基金資助項目(13ZR 1440800)

石志東(1964—),男,研究員,博士生導師,博士,研究方向為光纖通信和傳感器網絡等.

E-mail:zdshi@shu.edu.cn