2017年高考全國理綜卷Ⅰ第21題的解析和思考
余勝軍(保定市教育科學研究所 河北 保定 201000)(收稿日期:2017-08-09)

2017年高考全國理綜卷Ⅰ第21題的解析和思考
余勝軍
(保定市教育科學研究所 河北 保定 201000)
(收稿日期:2017-08-09)
2017年高考全國理綜卷Ⅰ第21題,考查常規的三力動態平衡問題,但是在用常規的正交分解法或者矢量三角形方法解決此題時,卻會遇到較大的麻煩.用多種方法解答了此題,并對解題方法進行歸納總結.
三力平衡 正交分解 矢量法則
1 試題及其情境分析

圖1 題圖

( )
A.MN上的張力逐漸增大
B.MN上的張力先增大后減小
C.OM上的張力逐漸增大
D.OM上的張力先增大后減小
本題是一個常規的三力動態平衡問題,常用的方法是正交分解法,即以物體為研究對象,建立直角坐標系,把3個力沿兩個坐標軸進行分解,根據質點平衡原理列出兩個坐標軸上的平衡方程,根據角度的變化判斷力的變化.其次是用矢量三角形方法,3個力平衡,通過平移后,3個力的矢量線段將組成首尾銜接的三角形,根據三角形的邊、角變化來判斷力的變化.
但是筆者分別用兩種解題方法進行解答,發現如下問題:
(1)用正交分解法解答本題時,首先是確立變量角度的問題,在動態變化的受力分析圖中,找到合適的變量角度不容易.其次是平衡方程的建立,找到角度的幾何關系是關鍵.最后是根據數學三角函數的各種變化推導,這對三角函數及其變換有很高的要求,且用時較長,高考答題過程中考生很難平心靜氣地逐步解答此題.因為性價比太低,遠超6分的題目應該消耗的時間.
(2)用矢量三角形方法解答本題時,作出某時刻的矢量三角形很容易,但是要找到連續變化的矢量三角形之間的關系卻不容易,關鍵是不能迅速找到三角形中變量和不變量的關系,或者是找不到畫連續變化三角形的參考線或輔助線.
接下來,筆者將用兩種方法解答此題并進行詳細的闡述.
2 正交分解法解題
解法1:建立常規的水平豎直方向的直角坐標系
以重物為研究對象,轉過較小角度和較大角度時受力情況如圖2(a)、(b)所示.


(1)
豎直方向上

(2)

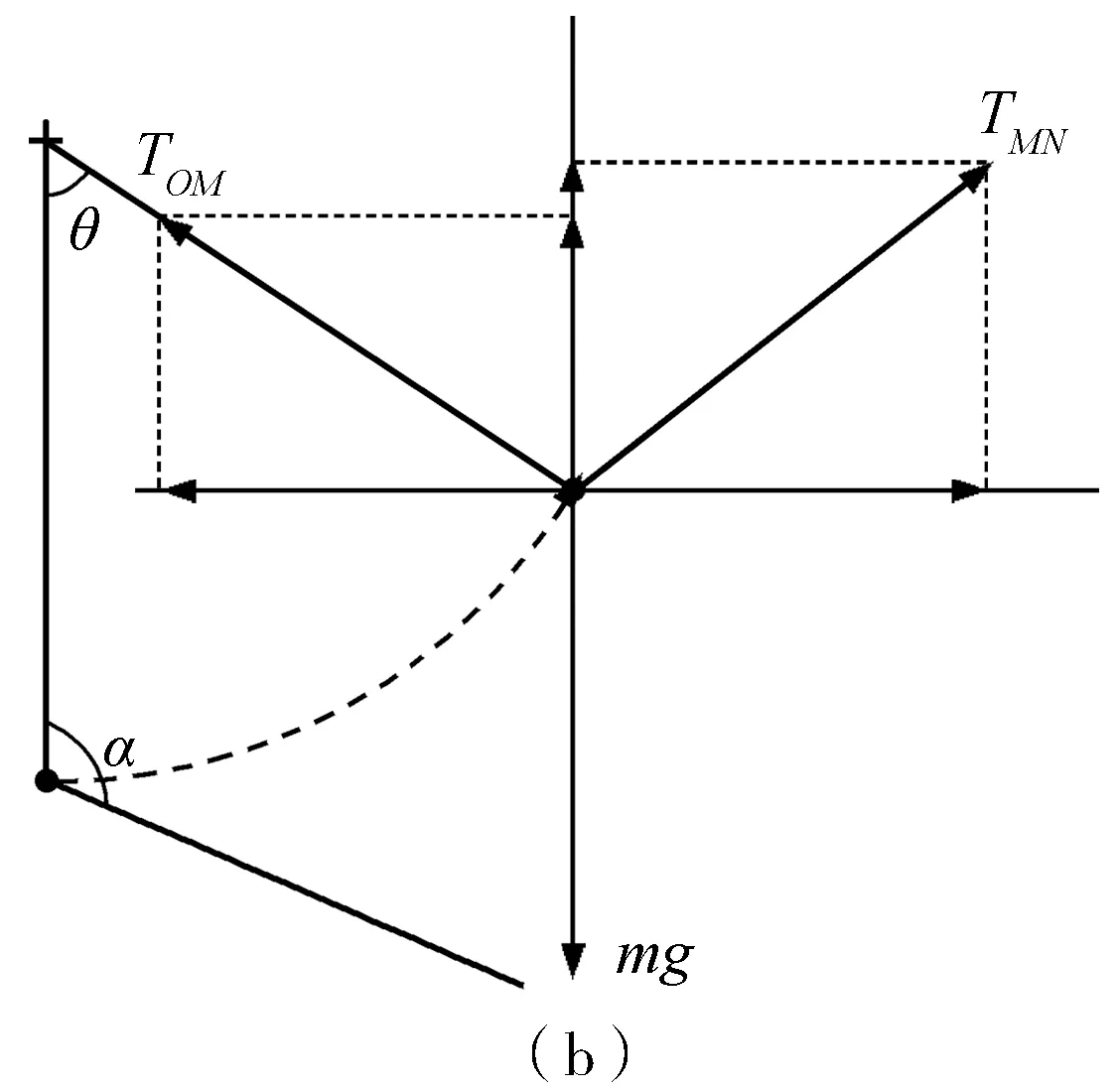
圖2 解法1受力分析圖
水平方向上
TOMsinθ=TMNsin(α-θ)
(3)
豎直方向上
TOMcosθ=mg-TMNcos(α-θ)
(4)
式(3)除以式(4)得
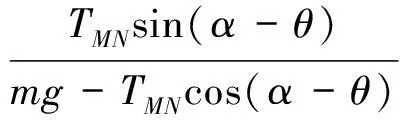
整理得到

再利用三角函數的兩角和差公式進一步整理

即

(5)
代入式(3)得到

(6)
由題設條件和式(5)、(6)知道,mg和α是不變量,隨著θ角增大,TMN一直增加,所以MN的張力一直增大;當α-θ等于90°時TOM達到最大值,所以OM上的張力先增大后減小.正確答案為A和D.
對圖2(b)所示,根據平衡有:水平方向上
TOMsinθ=TMNsin(α-θ)
豎直方向上
TOMcosθ+TMNcos(α-θ)=mg
由此可見,上面兩個表達式跟式(3)、(4)一樣,也就是說轉過的角度大小不影響平衡方程的最終表達,圖2(a)、(b)結論歸一.
綜合觀察上面的解法,顯而易見,如此解答,耗時耗力,不經濟!我們都知道,建立直角坐標系時坐標軸方向的選擇是任意的,以分解力的數量少和簡化解題過程為原則.那么本題建立坐標系能不能選別的方向呢?請看下面解答.
解法2:選擇另外兩個力為坐標系的其中一軸(估計想到此法的考生不多)
如圖3(a)所示,選擇OM的方向為y軸,垂直OM方向為x軸,如此選取坐標軸的意義在于:在x軸上平衡,只有TMN和mg兩個力的分力,不涉及第三個力,直接找到變量關系.由幾何關系直接得到

(7)
如圖3(b)所示,選擇MN的方向為x軸,垂直MN方向為y軸,如此選取坐標軸的意義在于:在y軸上平衡,只有TOM和mg兩個力的分力,不涉及第三個力,直接找到變量關系.由幾何關系直接得到

(8)
整理式(7)、(8),同樣得到式(5)、(6).
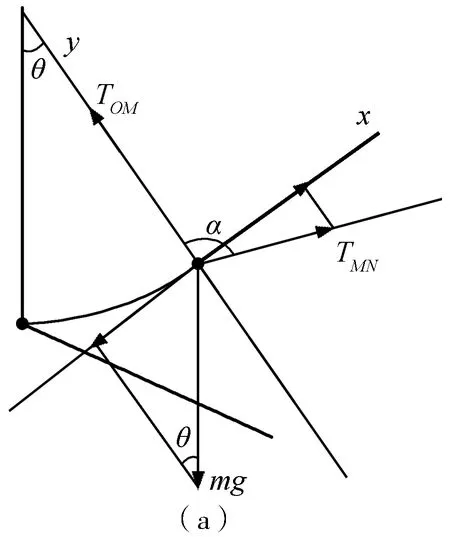

圖3 解法2換方向建立坐標軸
由此可見,靈活選取坐標軸的方向建立坐標系,有時候是能夠簡化分析過程和推導過程的.
3 矢量法解題
矢量法解題,就是利用力的示意圖或圖示,直接根據平行四邊形或者三角形圖形及其幾何關系直觀得出結論的方法.
解法3:矢量三角形
以重物為研究對象,緩慢拉起,重物處于平衡狀態.受力分析后平移FOM和FMN得到矢量三角形如圖4所示,由三角形正弦定理得

(9)

圖4 矢量三角形法分析圖
由題設條件知道θ=π-α,α是定值,重力大小方向不變,所以這是一個定值等比式.緩慢拉起的過程中γ先減小到90°,再繼續減小,β一直增大,所以FOM先增大后減小,FMN一直增大.
用此方法解題的難點之一便是確定θ是定值,作圖時有些必要輔助線能幫助我們迅速找到關系.另外一個難點是根據物理情確定三角形角度的變化情況.
解法4:利用參考圓解題
由解法3知道,重力矢量長短及方向不變,矢量三角形中重力所對的角度在緩慢抬起的過程中不變,根據圓的幾何性質知道,可以把重力矢量看成某圓的一條固定弦,另外兩個力的首尾銜接點在該圓周上,根據圓周角定理知道,重力所對圓周角不變,跟解法3的結論完全一致.畫出典型的矢量三角形圖像如圖5所示,當MN水平時,OM恰好過圓心,此時FOM矢量達到最大值,所以FOM先增大后減小,FMN矢量所對圓周角逐漸增大,所以其大小逐漸增大.

圖5 用參考圓解題分析圖
解法5:利用等效思想解題
在緩慢抬起MN的過程中,MN與OM的夾角不變,兩繩子張力的合力G大小和方向均不變,為了使得作圖方便,看起來直觀,可以用合力G順時針偏轉來等效替代繩子的逆時針旋轉.這樣,G矢量一端的軌跡構成參考圓,半徑為G,如圖6所示.把初始狀態的MN平行向外平移,與圓周相切于Q點.

圖6 利用等效思想解題分析圖
由圖可知TOM矢量端點由A到B,達到最大值,然后依次下降到C,D,E,所以TOM先增大后減小.而TMN端點依次向外為A1,B1,C1,D1,E1,逐漸增大.
解法4的難點是想到參考圓,解法5的難點是想到等效替代的思想和畫出參考圓,并找到直徑OM(解法4)和切線QB(解法5)這個臨界條件.
4 解題反思與啟示
以上是筆者想到的5種解法、兩種思路.其中解法1和解法2為比較常規的方法,從物理規律入手,當然推算過程稍顯復雜;解法3、解法4和解法5,思考起點雖是物理受力分析和平衡規律,但解題入手點和思維方法卻更偏重于幾何知識,典型的應用數學解決物理問題,是數學物理方法,其難點在于能否根據物理情景迅速抽象出幾何模型,并在幾何模型中找到變量關系.很顯然,前兩種解法很規矩,后面3種解法更直觀簡便,但是解答難度相差無幾,能用什么方法關鍵在于考生自己的能力結構,和本題考查的知識結構相關度不大.
如何形成優良的能力結構?筆者想,除了扎實的物理基本功底之外,還在于學生有足夠多實踐機會,在關鍵時候得到恰當的點撥,絕不是教師喋喋不休,代審題、代解題等包辦代替的教學活動能夠形成的.所以設置合適的物理情境,采用一題多解、多題歸一的教學活動,給予學生思考、動手動腦的機會,實戰中一定會形成學生優良的能力結構.而且學生對數學知識應該會比教師更熟悉,欠缺的只是跟物理模型的結合訓練而已,一旦學生掌握用某種數學工具解決物理問題,一定會比教師解決得更快.

