基于高階Cauchy-Born準則的平面應變梯度結構監測理論研究★

呂 娜 侯東昌 孫玉周

(中原工學院建筑工程學院，河南 鄭州 450007)

基于高階Cauchy-Born準則的平面應變梯度結構監測理論研究★

呂 娜 侯東昌 孫玉周

(中原工學院建筑工程學院，河南 鄭州 450007)

應用高階Cauchy-Born準則，通過建立新舊坐標系下平面矢量的坐標轉換公式，推導新坐標系下應變梯度的關系式，為應變梯度傳感器的應用提供了理論基礎，為結構監測提供了新方法。

結構健康監測，光纖光柵傳感器，應變梯度，高階Cauchy-Born準則

0 引言

近年來，隨著我國土木工程的繁榮發展，工程結構的健康監測問題成為一項越來越重要的研究。智能結構健康監測技術將先進傳感技術與被測結構本身特性相結合，實現對結構服役狀態、損傷程度的監測以及對損傷位置的判定[1]。在用于監測結構健康的傳感器領域中，光纖光柵傳感器發展迅速，廣泛應用于土木工程結構健康監測中。目前，光纖光柵已經用來做成位移、應變、溫度傳感器，并且已相當成熟，而光纖光柵應變梯度傳感器還處于探索階段，雖然有人提出應變梯度傳感器，但現在還沒有發現關于光纖光柵應變梯度傳感器得以實際應用的報道。

光纖光柵傳感器質量輕、體積小，具有性能穩定、多參數測量、分布測量等優點，光纖光柵傳感器的無電磁干擾、可測量多種信號、易于分布埋入結構和構成網絡等特性，使其成為能夠用于長期結構監測的理想傳感元件[1]。這為開發新型傳感器提供了可能。

大量疲勞試驗表明，結構在其使用期限內70%的損傷始于初始裂紋。伴隨著裂紋擴展，結構的強度與剛度也將不斷劣化，最終導致突發性災難事故。線彈性材料裂紋尖端的應變場具有r-1/2奇異性，應變梯度相對于應變其變化更加劇烈，具有更高階的奇異性r-3/2[3]。相比傳統的應變損傷識別，應變梯度的監測具有更加敏感、更早捕捉損傷的優勢。

近年來，很多研究人員開始運用各種原理，注重于開發設計新型應變梯度傳感器，并關注存在于大量生物材料、高分子材料以及晶體材料中的撓曲電效應[4,5]，目前已開發出幾種可測量應變梯度的傳感器，如鈦酸鍶鋇(BST)應變梯度傳感器[6,7]，應變梯度測量方面的研究還未見報道。若要將光纖光柵應變梯度傳感器用于工程實際中，還需要解決一些問題，如已知該狀態下的應變梯度，如何確定任意方向的應變梯度，最大應變梯度該如何確定等問題。本文應用高階Cauchy-Born準則，通過建立新舊坐標系下平面矢量的坐標轉換公式，推導新坐標系下應變梯度的表達式，為應變梯度傳感器的使用提供理論基礎。

1 Cauchy-Born準則

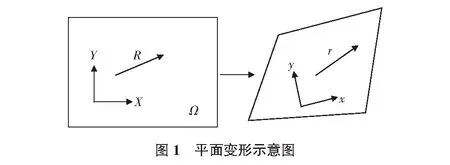
在結構變形中建立坐標系如圖1所示，X=(X，Y)表示原始參考構形，x=(x，y)表示當前構形。結構從平面到曲面的變形映射由x=x(X)定義，其一階和二階變形梯度為：

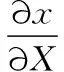
(1)

其中，i=1，2；J，K=1，2。

將一階變形梯度F進行展開，形式如下：

(2)

將二階變形梯度G進行展開，形式如下:

(3)

在經典Cauchy-Born準則中，變形前的矢量R和變形后的矢量r可通過一階變形梯度F表示為[8]:

r=F·R

(4)

原始參考構形中矢量R的起點為X，變形后當前構形中的矢量r可以準確表示為：

r=x(X+R)-x(X)

(5)

對x(X+R)做關于X的泰勒級數展開，可得:

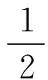
(6)

將式(6)代入式(5)，保留二階項可得:

(7)

式(7)即為高階Cauchy-Born準則下變形后的矢量近似表達式[10]。相對于經典Cauchy-Born準則，這里增加了一個基于二階變形梯度的修正項。如果要提高近似解的精度，還可以附加更多的高階項。

對彎曲或扭轉的研究表明，桿件的最大應力往往發生于構件表層，由于構件表面一般為自由表面，即有一主應力等于零，因而從構件表層取出的微分單元體單元就接近二向應力狀態。所以在工程監測中選擇在構件表面測量與二向應力成比例的二向應變具有理論與埋設難易程度的實際意義。本文提出的應變梯度傳感器可粘貼在構件表面工作，因而應變梯度的分析可以視為平面問題處理，可將光纖光柵看做方向矢量進行研究。

2 應變與應變梯度

在平面坐標系Oxy中，方向矢量R(X,Y)經變形成為r(x,y)。由應變的定義可知[11]：

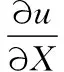
(8)

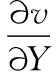
(9)

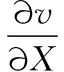
(10)

將式(8)～式(10)代入一階應變梯度表達式(2)，可得:

本文研究基于的數據是1996—2017年，2018年的中美貿易戰對中國石油安全也帶來了影響，后期筆者將做進一步的研究。

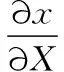
(11)

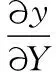
(12)

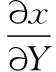
(13)

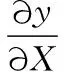
(14)

將式(11)～式(14)代入經典Cauchy-Born準則表達式(4)，展開寫成分量形式為:

x=(1+εX)X+θXYY

(15)

y=θYXX+(1+εY)Y

(16)

將式(11)～式(14)代入高階Cauchy-Born準則表達式(7)，展開寫成分量形式為:

(17)

(18)

在坐標系OXY中，方向矢量R(X,Y)變形后方向為矢量r(x,y)，長度由|R|變為|r|，與X軸正方向夾角為α，則有:

X=|R|cosα,Y=|R|sinα

(19)

假設將坐標軸旋轉α角(逆時針方向為正)，得到新坐標系Oxy(見圖2)，方向矢量R(X,Y)變形后為r(x,y)，長度仍然由|R|變化為|r|，則有:

X|α=|R|,Y|α=0

(20)

將式(19)代入式(15)，式(16)得:

x=(1+εX)|R|cosα+θXY|R|sinα

(21)

y=θYX|R|cosα+(1+εY)|R|sinα

(22)

將式(20)代入式(15)，式(16)得:

x|α=(1+εX|α)·|R|,y|α=θYX|α·|R|

(23)

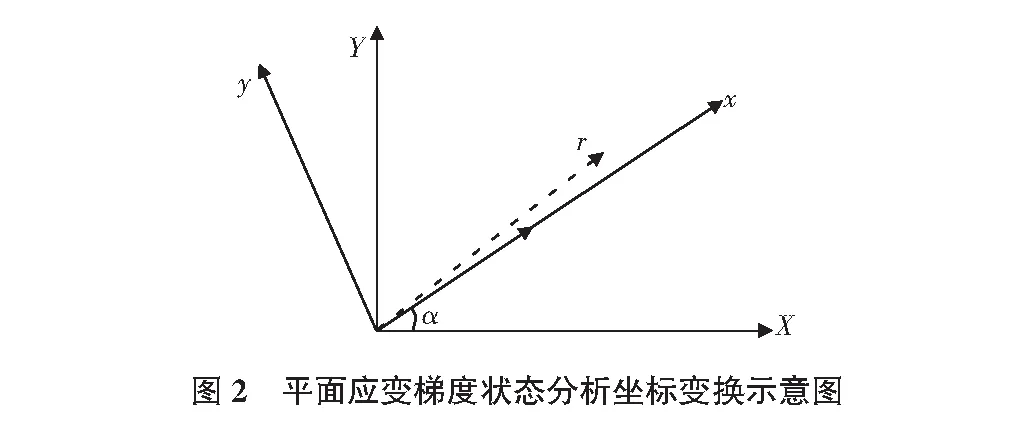
新舊坐標系下矢量坐標變換關系為:

x|α=xcosα+ysinα

(24)

y|α=-xsinα+ycosα

(25)

εX|α=εXcos2α+εYsin2α+γXYsinαcosα

(26)

式(26)即為平面應變狀態下任意方向線應變表達式。

將式(19)代入式(17)，式(18)得:

(27)

(28)

將式(20)代入式(17)，式(18)得:

(29)

(30)

將式(27)～式(30)代入式(24)，化簡得:

(31)

式(31)減去式(26)，化簡得:

G111|α=G111cos3α+G222sin3α+
(G122+2G212)cosαsin2α+(G211+2G112)cos2αsinα

(32)

由式(32)可以計算分析α方向上的應變梯度，在平面上任意一點，通過6個應變梯度和角度關系即可表示出來該變形狀態下任意方向的應變梯度。

當不考慮高階梯度，應用經典Cauchy-Born準則，結論退化為平面應變狀態下任意方向線應變表達式，這驗證了式(32)推導結果的正確性。

由于應變梯度是最敏感的測量對象，通過對式(32)的應用，應變梯度的有效量測為掌控結構健康監測中裂縫的發生與生長情況提供了新途徑。

3 結語

本文應用高階Cauchy-Born準則，通過代入新舊坐標系下平面位移矢量的坐標轉換公式，推導出了新坐標系下應變梯度的表達式，即任意方向上的應變梯度可通過該變形狀態下的6個應變梯度和角度來表示。該理論為使用應變梯度理論制作光纖光柵應變梯度傳感器進行結構健康監測的應用提供了理論基礎。

為了更好地分析預測結構損傷，下一步我們將深入分析最大應變梯度該如何確定。

[1] 付興權,干鵬飛.光纖健康監測技術在橋梁結構中的發展與應用[J].山西建筑,2015，41(26):166-167.

[2] 李宏男,李東升,趙柏東.光纖健康監測方法在土木工程中的研究與應用進展[J].地震工程與工程振動,2002,22(6):76-83.

[3] Staszewski D W,Lecturer.Monitoring on-line integrated technologies for operational reliability-monitor[J].Air & Space Europe,2000,2(4):67-72.

[4] 李 康,駱 英,徐晨光.基于BST微懸臂梁橫向撓曲電系數的測定[J].壓電與聲光,2014(5):798-800.

[5] Baskaran S,He X,Chen Q,et al.Experimental studies on the direct flexoelectric effect in α-phase polyvinylidene fluoride films[J].Applied Physics Letters,2011,98(24):901-903.

[6] Kwon S R,Huang W B,Zhang S J,et al.Flexoelectric sensing using a multilayered barium strontium titanate structure[J].Smart Materials & Structures,2013,22(11):2870-2876.

[7] Huang W,Yan X,Kwon S R,et al.Flexoelectric strain gradient detection using Ba0.64Sr0.36TiO3 for sensing[J].Applied Physics Letters,2012,101(25):2903-2907.

[8] 趙亞溥.表面與界面物理力學[M].北京：科學出版社,2012.

[9] 范鏡泓.材料變形與破壞的多尺度分析[M].北京:科學出版社,2008.

[10] Sun Y,Liew K M.The buckling of single-walled carbon nanotubes upon bending:The higher order gradient continuum and mesh-free method[J].Computer Methods in Applied Mechanics & Engineering,2008,197(33-40):3001-3013.

[11] 徐秉業.應用彈塑性力學[M].北京：清華大學出版社,1995.

Planestraingradientanalysisbasedonhigher-orderCauchy-Bornrule★

LvNaHouDongchangSunYuzhou

(SchoolofCivilEngineeringandArchitecture,ZhongyuanUniversityofTechnology,Zhengzhou450007,China)

In this paper, by using the high-order Cauchy-Born rule and the coordinate transformation formula of plane vector in the new and old coordinate systems, the expression of strain gradient in the new coordinate system is derived, which provides a theoretical basis for the application of strain gradient sensors.

structure health monitoring， sensor, strain gradient, higher-order Cauchy-Born rule

TU196

：A

1009-6825(2017)24-0030-03

2017-06-15 ★ ：國家自然科學基金(11472316)；河南省科技創新人才項目(164200510020)

呂 娜(1991- )，女，在讀碩士； 侯東昌(1991- )，男，在讀碩士； 孫玉周(1974- )，男，博士，教授