勵磁系統PID控制模型的選型探討
(陜西渭河發電有限公司, 陜西 咸陽 701208)
勵磁系統PID控制模型的選型探討
李明強
(陜西渭河發電有限公司, 陜西 咸陽 701208)
發電機勵磁系統在電力系統靜態及動態穩定性方面發揮巨大作用。如何根據勵磁方式選擇合適的勵磁系統PID模型,基于勵磁系統方式控制模型選型的盲目性及經濟性考慮,從現行的自并勵和勵磁機勵磁系統分別對勵磁系統串聯的PID控制模型進行比較,研究選用一級超前-滯后或選用兩級超前-滯后對于勵磁系統的影響,并分別對其進行仿真。結果表明,自并勵系統選擇一級超前-滯后完全可以滿足勵磁系統要求,勵磁機系統更宜選擇兩級的超前-滯后模型。研究結果對發電機勵磁系統控制設備選型給予一定的參考。
勵磁機系統; 自并勵系統; PID; 控制模型
0 引 言
近年隨著國家新建火電機組向高容量大參數發展,自并勵勵磁系統、常規勵磁機勵磁系統及核電機組普遍采用的無刷勵磁系統得到了長足發展[1-3],勵磁系統穩定性對電網安全及其穩定性發揮巨大作用[4-5],因此選擇一種經濟可靠的發電機勵磁系統設備顯得更加的重要。勵磁系統控制設備中,PID直接影響勵磁系統性能指標。針對電站勵磁系統的方式的不同,下面將以IEEE標準的串聯PID[6]為例,分別解析一級超前-滯后補償器的PID和兩級超前-滯后補償器的PID特性,并對其進行仿真計算,在不同的勵磁系統方式下為選擇一種經濟合理的勵磁控制設備提供參考。
1 自并勵勵磁系統的PID控制模型
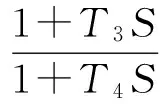
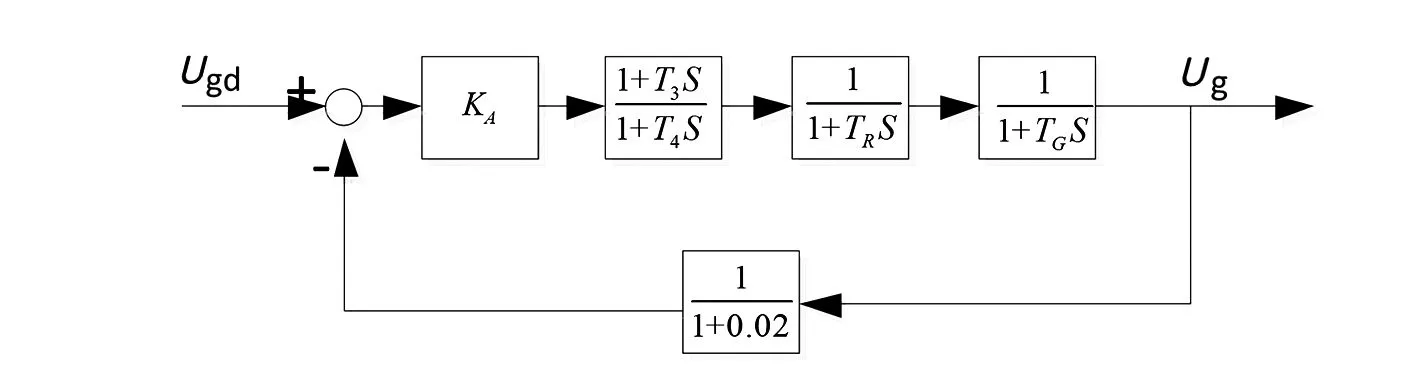
圖1 一級超前-滯后補償器的自并勵勵磁系統的模型
取KA=200、T3=1 s、T4=4 s、TR=0.02 s、TG=6 s,利用MATLAB[7]軟件對此自并勵勵磁統的動態性能指標進行仿真計算。
圖2為開環頻率特性的Bode圖,圖3為發電機單位階躍響應特性圖。
仿真結果見表1,可以得出在自并勵勵磁系統的自動調節器中,只需一級超前-滯后補償器,就可以使勵磁系統獲得優良的性能指標。
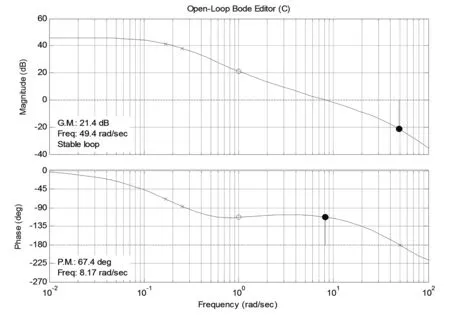
圖2 一級超前-滯后補償器自并勵勵磁系統Bode圖
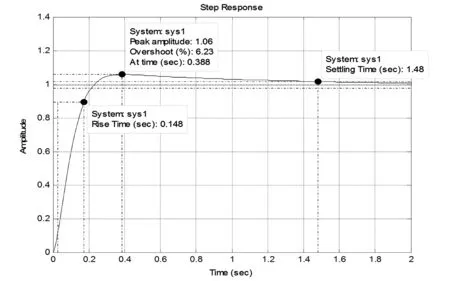
圖3 一級超前-滯后補償器下自并勵發電機單位階躍響應圖
表1一級超前-滯后補償器自并勵勵磁系統仿真結果
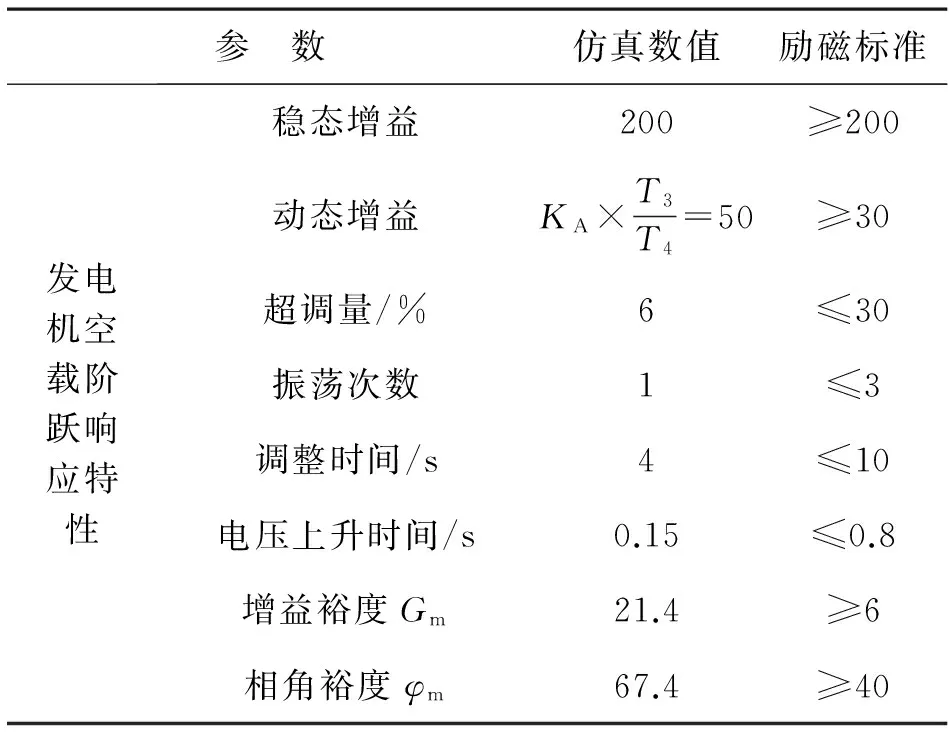
參 數仿真數值勵磁標準發電機空載階躍響應特性穩態增益200≥200動態增益KA×T3T4=50≥30超調量/%6≤30振蕩次數1≤3調整時間/s4≤10電壓上升時間/s0.15≤0.8增益裕度Gm21.4≥6相角裕度φm67.4≥40
2 勵磁機勵磁系統PID控制模型
2.1勵磁機勵磁系統采用一級超前-滯后補償器
從控制系統結構上看,相比于自并勵勵磁系統,勵磁機系統中多了勵磁機環節,然而勵磁機時間常數會對勵磁控制系統的穩定運行和動態性能指標產生很大影響[8],采用一級超前-滯后補償器的勵磁機勵磁系統閉環控制系統的簡化模型框圖見圖4。
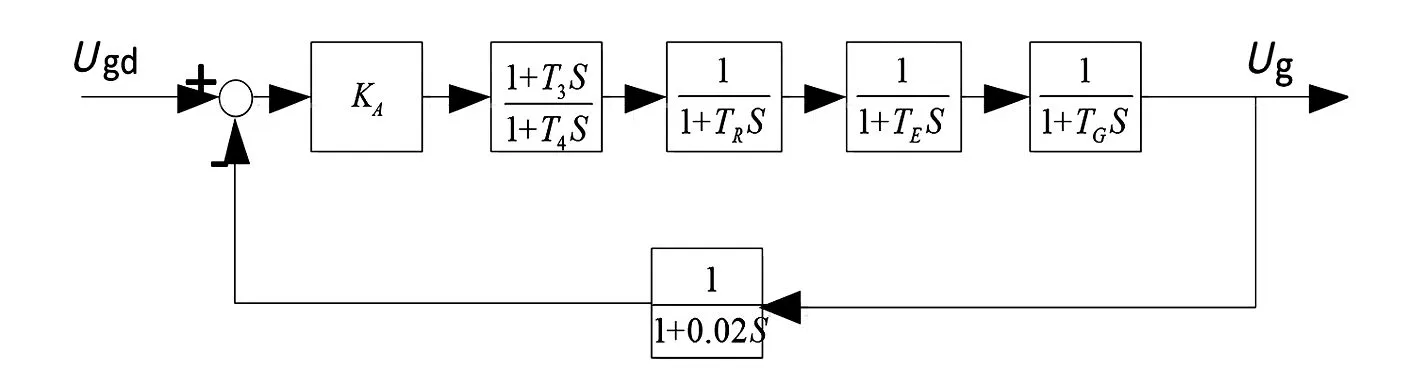
圖4 一級超前-滯后補償器勵磁機勵磁系統的模型框圖
下面利用MATLAB軟件,對此勵磁機勵磁系統的動態性能指標進行仿真計算。
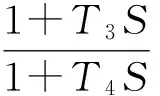
圖5為所選超前-滯后補償參數下的開環頻率特性的Bode圖,圖6為相應的發電機單位階躍響應特性圖,表2是仿真結果數據。
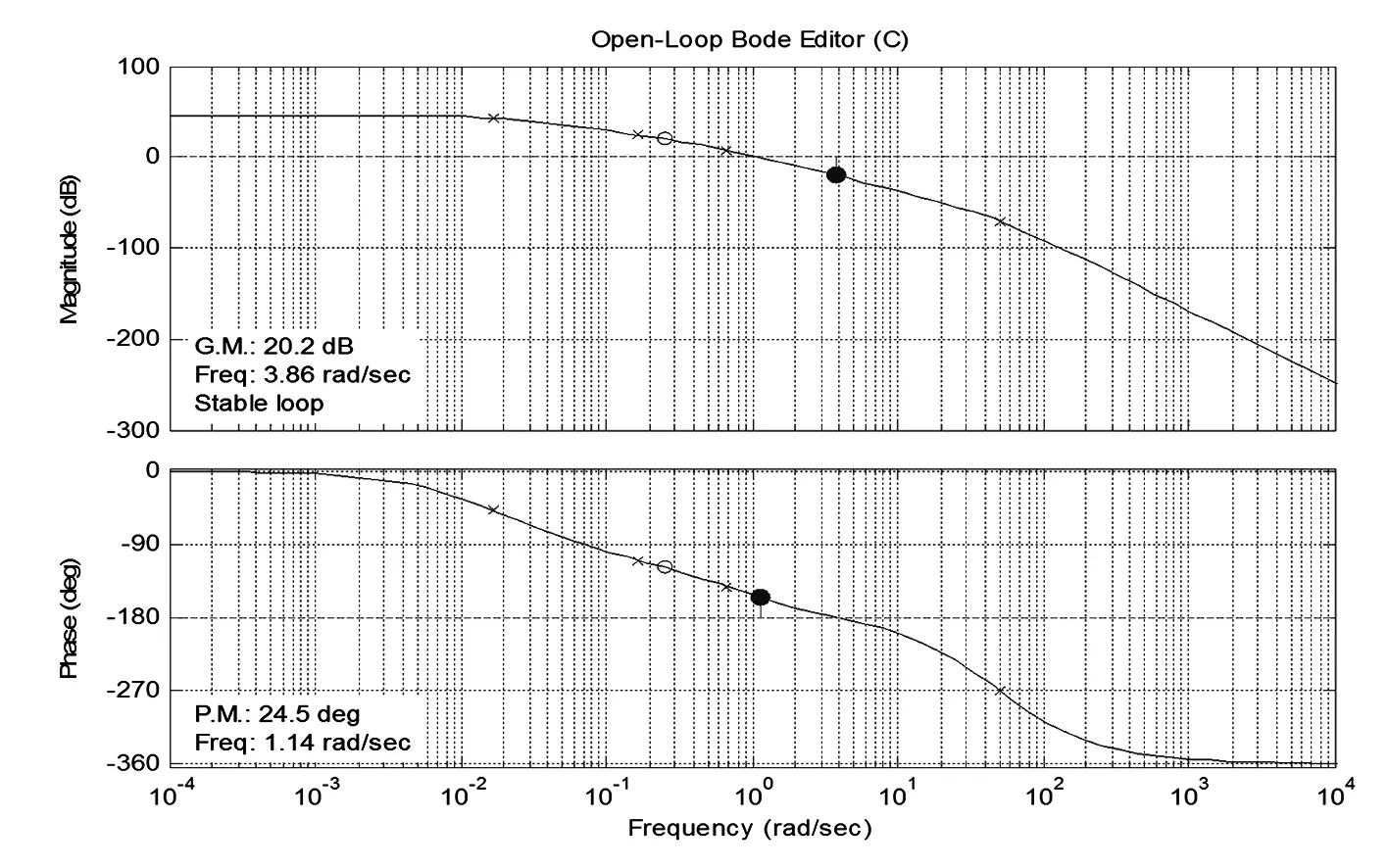
圖5 一級超前-滯后補償器下勵磁機勵磁系統Bode圖
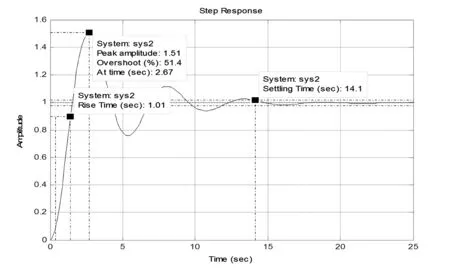
圖6 一級超前-滯后補償器下發電機單位階躍響應圖
顯然,在勵磁機勵磁系統中,選用一級超前-滯后補償器遠不滿足標準對勵磁系統性能指標的要求,并且增益裕度和相角裕度數值較小勵磁系統穩定性較差[9],因此在勵磁機勵磁系統中選用的兩級超前-滯后補償器勢在必行。
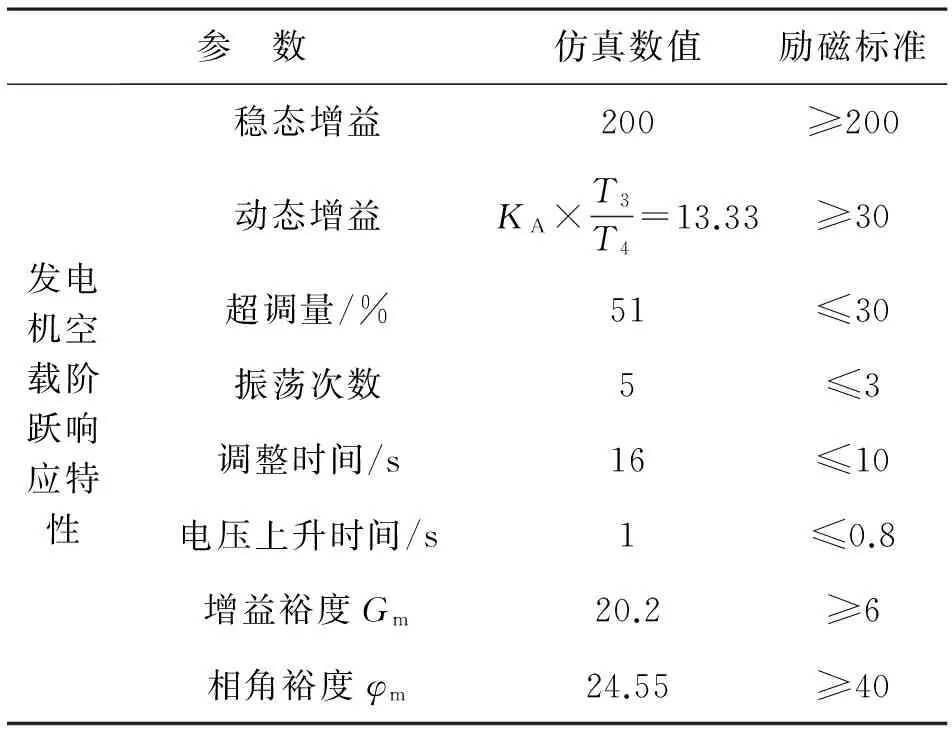
表2 一級超前-滯后補償器勵磁機勵磁系統仿真結果
2.2勵磁機勵磁系統采用兩級超前-滯后補償器
采用兩級超前-滯后補償器的勵磁機勵磁系統的閉環控制系統的簡化模型框圖如圖7所示。
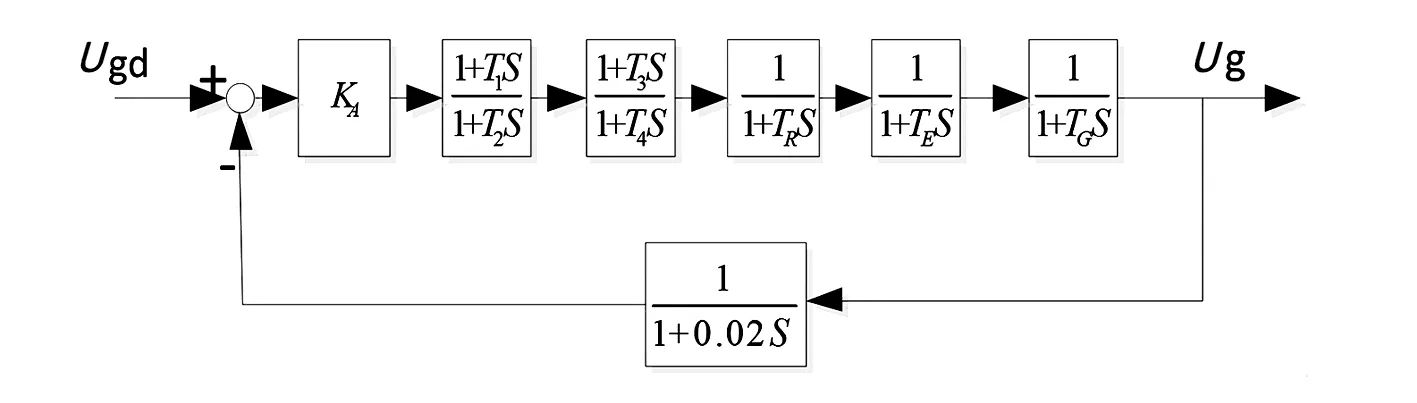
圖7 兩級超前-滯后補償器勵磁機勵磁系統的模型框圖
以同樣的機組數據,利用MATLAB軟件,對此勵磁機勵磁系統的動態性能指標進行仿真計算。
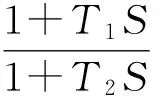
下面列舉幾組滿足勵磁標準的兩級超前-滯后參數:
1)T1=0.6 s,T2=0.08 s,T3=2 s,T4=10 s;
2)T1=0.6 s,T2=0.08 s,T3=3 s,T4=15 s;
3)T1=0.6 s,T2=0.08 s,T4=4 s,T4=20 s;
4)T1=0.6 s,T2=0.08 s,T4=6 s,T4=30 s。
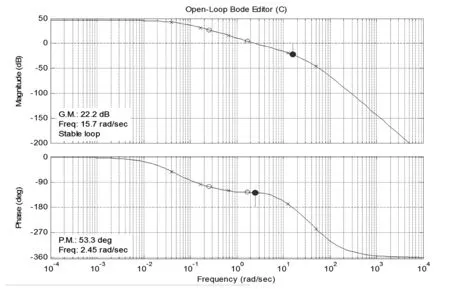
圖8 兩級超前-滯后補償器下勵磁機勵磁系統Bode圖
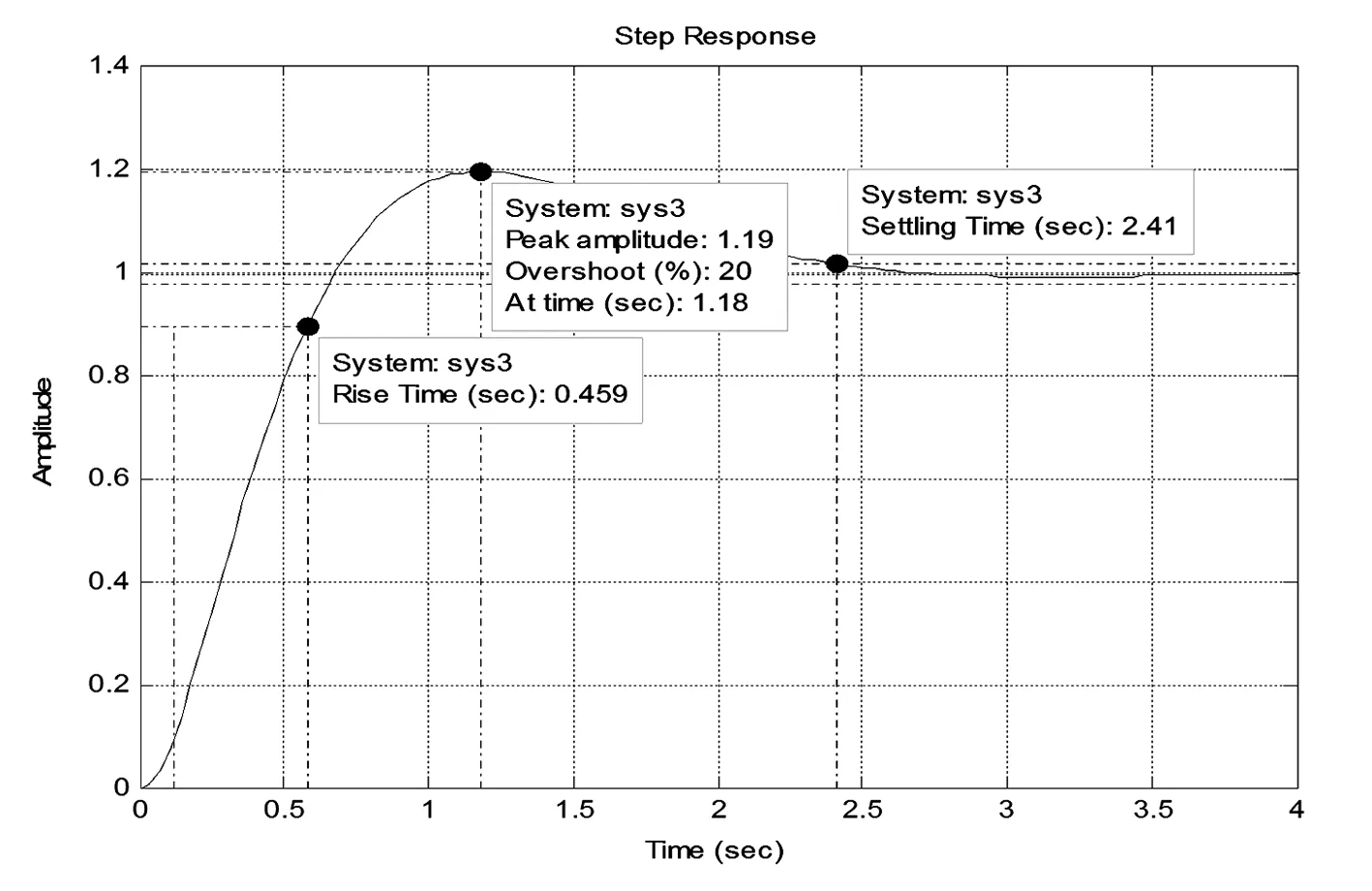
圖9 兩級超前-滯后補償器下發電機單位階躍響應圖
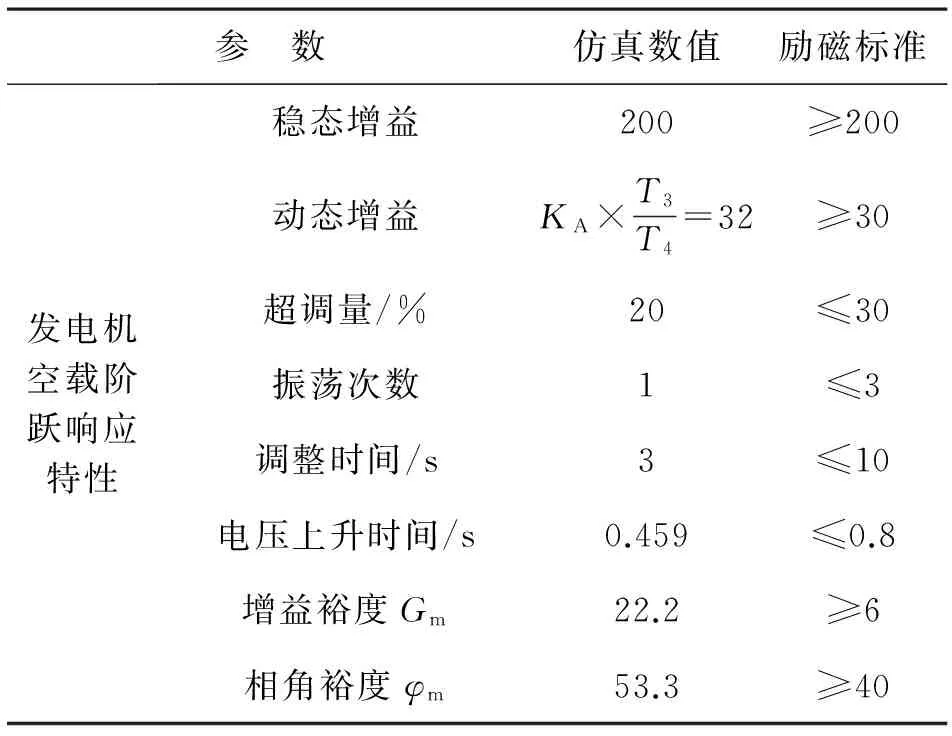
參 數仿真數值勵磁標準發電機空載階躍響應特性穩態增益200≥200動態增益KA×T3T4=32≥30超調量/%20≤30振蕩次數1≤3調整時間/s3≤10電壓上升時間/s0.459≤0.8增益裕度Gm22.2≥6相角裕度φm53.3≥40
綜合以上分析,在勵磁機勵磁系統中,必須采用兩級超前-滯后補償器才可得到優良的勵磁系統性能指標,總結選擇兩級超前-滯后補償器參數原則如下:
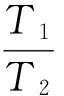
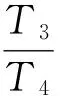
可見在勵磁機勵磁系統中采用兩級超前-滯后補償器很容易選擇合適參數滿足系統要求。
3 結 語
通過對比不同結構的勵磁系統及相應的勵磁系統中的各環節物理量在傳遞函數中參數的意義,對其PID進行仿真計算。在自并勵勵磁系統中選擇一級的超前-滯后補償器完全可以滿足勵磁系統的各項性能指標;在勵磁機勵磁系統及無刷勵磁系統中選擇兩級的超前-滯后補償器,更易選擇適合的參數來滿足勵磁系統性能指標。
[1] 薛學斌. 1 000 MW機組發電機勵磁方式的選擇[J]. 電工技術, 2008(1):59-60.
[2] 馮旭. 大型汽輪發電機制造中的勵磁方式選型[J]. 科技創新與應用,2013(7):74.
[3] 張玫,朱方,劉增煌. 大型汽輪發電機采用自并勵勵磁系統的可行性分析[J]. 電網技術,1997,12(21):38-44.
[4] 劉取. 電力系統穩定性及發電機勵磁控制[M]. 北京: 中國電力出版社, 2007.
[5] 霍承祥,劉增煌. 勵磁系統靜態放大倍數和發電機有功功率對調差的影響分析[J].電力系統自動化,2011,35(2):93-96.
[6] IEEE Recommended Practice for Excitation System Models for Power System Stability Studies[S]. IEEE Power Engineering Society,IEEE 3 Park Avenue New York, NY 10016-5997, USA, 21 April 2006:10-20.
[7] 張德豐. MATLAB控制系統設計與仿真[M]. 北京:電子工業出版社,2009.
[8] 郝正航,陳卓,邱國躍,等. 勵磁機時間常數對電力系統動態穩定性的影響[J]. 電工電能新技術, 2006, 25(1):26-29.
[9] 方思立,蘇為民. 勵磁系統動態性能指標有關標準的分析[J]. 電力設備, 2004, 5(7):39-40。
Excitation system of generator plays a significant role in the static and dynamic stability of power system. How to choose the right PID model according to the excitation mode of excitation system, and considering the blindness and economy of control model selection based on excitation system modes, the PID control models series with excitation system are compared from the current self-shunt excitation system and exciter excitation system. The influence of selecting first-order lead-lag and second-order lead-lag on excitation system is studied, and its simulation results show the self-shunt excitation system selecting first-order lead-lag can fully meet the requirements of excitation system, and exciter excitation system selects second-order lead-lag model, which gives a reference to control equipment selection for generator excitation system.
exciter excitation system; self-shunt excitation system; PID; control model
TM621
:A
:1003-6954(2017)04-0087-04
2017-03-16)
李明強(1983),助理工程師,主要研究方向為繼電保護與勵磁控制。

