論地理課中時間問題之解決

楊耀英

時間問題是歷屆學生的普遍難題，因時間雖非物質卻與運動有關，它有自然的變化規律，又有人為制定的規則。筆者經過多年的教學實踐和思考，總結出一套解決時間問題的方法——“兩點一線數軸法”。本文即是對此教學的總結，聊以分享和希冀指教。下面以問帶思，循序漸進，用問題說明“兩點一線數軸法”。

一、“兩點一線”——地方時的基準

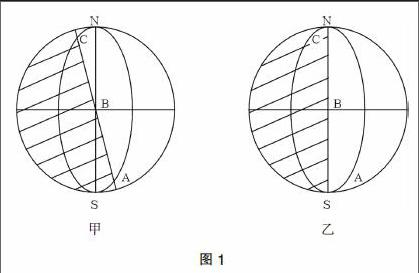
問題1：甲、乙兩圖（圖1）中的陰影表示黑夜，經線間隔相等，將A、B、C三點的地方時填在下面表中（表略）。

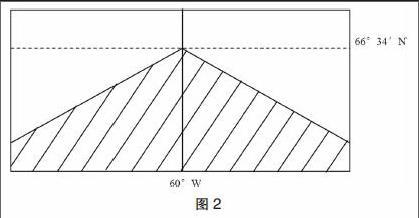
問題2：根據下圖（圖2）中的信息求出北京時間。

問題1主要是糾正部分學生的誤解，他們以為各地全年日出（在晨線上）都是6時，日落（在昏線上）都是18時，而忘了不同經線的地方時不同。晨昏線是時刻變動的，以變動不居的晨昏線作為相對恒常有律的時間基準顯然不行。地方時以赤道為基準，此即“一線”，是利用了晨昏線的性質之一——晨昏線永遠平分赤道，所以赤道終年晝夜等長，每天6時日出，18時日落。以不變應萬變，地方時是以赤道為準，再以同一經線地方時相同來處理即可。

問題2是為了解決圖上（如圖2）若無赤道出現的時間問題。由此得出地方時的另一基準，即筆者所謂的“兩點”（正午12點和子夜0點），此“兩點”亦利用了晨昏線的另一性質——晨線和昏線的交接點是白晝的中間為正午12點和黑夜的中間為子夜24點（0點）。

結論：地方時的基準是“兩點一線”，所謂“兩點”是白晝的中間正午12點（時）和黑夜的中間子夜24（時）/0點（時）；“一線”是赤道，赤道亦看兩點，即赤道與晨線的交點是6點（時）、與昏線的交點是18點（時）。

二、兩點一線——日期的分界線

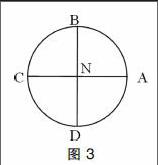
問題3：下面（圖3）是北半球的俯視圖，當A點的時間是21日12時，求B、C、D三點的時間。

很簡單，當A的時間是21日12時，B是21日18時，C是21日24時（同時是22日0時），D是22日6時。由此可見C所在的經線是日期的分界線，這條經線處于黑夜的中間（子夜），是筆者后面所謂的“兩點”——它同時是舊的一天（21日）的24點和新的一天（22日）的0點，此半夜的經線將地球分為兩個日期，該線以西是舊的一天，以東是新的一天。這是一條天然的日期的分界線。

但新的問題出現了，當D是22日6時，則A的時間是22日12時，B是22日18時……走向了無窮未來，逆向計算則可返回無盡過去。很明顯，同一地不可能同時是過去、未來的任一天（任一日期）的同一鐘點，如A同時是21日的12時，又是22日、23日……的12時，還是20日、19日……的12時。筆者的學生將此稱為“時間怪圈”（如下圖4）。

顯而易見，只有處于半夜的經線這一條日期的分界線是不夠的，它是一條天然的日期分界線。天然不足，唯以人為補之。如何人為補救呢？我們看問題4。

問題4：接上題及圖3，當A點是30°E時，求180°E和180°W的時間。

根據地球自轉的方向，人為規定了世界上日出最早（時間最早、最新）的地方是180°E，日出最遲（時間最晚、最舊）的地方是180°W。

由此，我們可得一時間箭頭如下，此即筆者要講的第三個“兩點一線”（亦即“兩點一線數軸法”的“數軸”），“兩點”是左端（西邊）的180°W和右端（東邊）的180°E，“一線”是將任一緯圈自經度180°處斷開拉直成一時間之箭，箭頭是180°E，箭尾是180°W，方向是地球自轉的方向自西向東，用此時間之箭（有限“數軸”）可計算任何時間問題（包括日期問題）。

用“數軸法”（如圖5）可立即計算得，180°E的時間是21日22時，180°W是20日22時。

180°E和180°W為何鐘點相同，日期卻相差一日（180°E比180°W早一日）？在數軸上一目了然，兩者首尾相距經度360°，經度15°一小時，所以相差24小時即剛好一日。

現在，再求（圖3）A、B、C、D各點的時間，當A點是30°E時，它們的時間就是唯一的了，除了C點既是20日24時又是21日0時。我們終于走出了“時間怪圈”，活在了當下，而不再會同時既是現在又是過去還是未來“三位一體”——那可是神。

結論：日期的分界線可概括為“兩點一線”，“兩點”是兩個鐘點，是處在半夜的經線的兩個時刻——同時既是舊的一天的24點又是新的一天的0點，它是一條日期的分界線，此線以西是舊的一天，以東是新的一天；“一線”是“日界線”（180°經線為主體），180°E比180°W早一日，鐘點相同，此線以西是新的一天，以東是舊的一天，“日界線”當然也是一條日期的分界線。

三、“兩點一線數軸法”——時間的計算方法

問題5：當廣州（23°N，113°E）的太陽升到最高時，當地的時間是幾點？

根據題目信息和已有知識，可知（1）太陽升到最高即正午，地方時是12點；（2）廣州的當地時間即北京時間，亦即120°E的地方時。所以問題可更簡明表述為：已知113°E的地方時是12時，求120°E的地方時。用“兩點一線數軸法”即可，求解如（圖6）。

問題6：班上某同學出生于10月5日9時，當時與他生日同一天的范圍是多大？

同樣用“兩點一線數軸法”，如（圖7）。

此法避開了“日界線”的繁瑣并可減少失誤，將那套人為的規定——什么早一天、遲一天、向西越過、向東越過、加一日、減一日……皆拋開不理，（“日界線”已被撇在了兩邊）只要在時間軸上找出0點（24點）即將地球分為新的一天和舊的一天的兩個范圍，此點以東至180°E為新的一天，以西至180°W為舊的一天。

結論：時間的計算用“兩點一線數軸法”，“兩點”是左端（西邊）的180°W和右端（東邊）的180°E，“一線”是將任一緯圈自經度180°處斷開拉直，成一時間之箭，箭頭是180°E，箭尾是180°W，方向是地球自轉的方向自西向東，用此時間之箭（有限“數軸”）可計算任何時間問題（包括日期問題）。

四、總結

將兩點一線數軸法的三種情況再簡單總結，如表。endprint