分數化運動模型在顱腦反常擴散中的初步應用
王振熊,許博巖,朱文珍*
分數化運動模型在顱腦反常擴散中的初步應用
王振熊1,許博巖2,朱文珍1*
作者單位:1. 華中科技大學同濟醫學院附屬同濟醫院放射科,430030 2. 北京大學磁共振成像研究中心,100871
擴散MRI (diffusion MRI,dMRI)在臨床上已得到了廣泛的應用,也是目前唯一能夠無創研究活體組織擴散過程的方法。傳統的磁共振擴散成像理論是基于經典的布朗運動模型,然而,研究表明生物體內的擴散過程實則為非布朗運動,也被稱為是“反常擴散”。為了解釋活體組織的反常擴散現象,一些模型被建立起來,在這些模型中,分數化運動(fractional motion,FM)模型被證實能夠恰當地描述生物體復雜環境中的反常擴散現象。借助其多參數(α 、β、μ、H)不僅能夠反映組織內分子反常擴散的情況,也可以提供組織結構豐富的細微變化信息,從而為疾病的診斷、治療及預后起到指導性的作用。作者旨在綜述基于FM模型的dMRI理論及其在評價顱腦反常擴散中的初步應用。
彌散磁共振成像;反常擴散;腦
傳統的擴散MRI (diffusion MRI,dMRI)原理是基于經典的布朗運動模型[1-2],它的均方位移與時間成線性關系,然而在復雜的生物細胞內,擴散過程已經被證實為非布朗運動,也稱為反常擴散[3-7]。反常擴散的均方位移與時間則是偏離線性的關系。為了描述這種反常擴散過程,一些理論模型被提出,比如連續時間隨機游走模型[8]、滲流集群或隨機障礙模型[9-10]、異質擴散過程模型[11-13],以及本文中的分數化運動模型[14]。單分子示蹤實驗的最新結果表明,分數化運動(fractional motion,FM)模型是目前描述細胞中擴散過程的最佳模型[15-18]。與傳統的DWI相比,FM模型借助其多參數值可以提供更豐富的組織微觀結構信息[19],從而為疾病的診斷、治療及預后起到指導性的作用。筆者以FM模型的基本理論及其在評價顱腦反常擴散中的初步應用予以綜述。
1 基于FM模型的dMRl理論
dMRI在臨床及科研中已經得到廣泛的應用,與其他常規的MR成像方法相比,dMRI已經探究到組織細胞的分子層面,其通過觀察水分子在組織內的擴散過程,從而為臨床提供生物組織微觀結構變化的信息。目前dMRI常常是用單指數模型來量化的,計算公式為:S/S0=exp(-b·ADC),其前提是假定生物組織內的水分子為自由擴散,且完全符合高斯分布。然而,大量的實驗已經證明,生物組織內水分子的運動因細胞間結構、細胞膜通透性以及游離水與結合水理化性質的差異而表現出的復雜化,并非自由擴散,MR擴散的信號衰減曲線也偏離單指數形式,尤其當b值較大(>1500 s/mm2)時,生物組織的不均質性對擴散運動的影響愈加明顯,水分子擴散位移偏離高斯分布的的趨勢也更加顯著[20]。為了更好地描述實驗結果,一些其他形式的模型被建立起來,其中包括雙指數模型[21-22]、拉伸指數模型[23]、統計模型[24]和峰度模型[25]。除了這些唯像的數學模型外,研究人員同時也嘗試利用一些基于反常擴散理論的物理模型來解釋這種信號衰減偏離單指數形式的現象[19,26-39]。FM模型就是其中之一,一些研究已經證實,FM模型是一個描述活體細胞中分子擴散過程較為理想的物理模型[15-18,30]。基于FM模型的dMRI理論[19]計算出的MR擴散信號衰減曲線公式為:

式中,Dα,H指廣義反常擴散的擴散系數,bα,H指廣義的b值。運用Stejskal-Tanner擴散序列[2],廣義的b值可以表達為:

式中,γ指磁旋比,G0表示擴散梯度幅度,△指擴散間隔時間,是無量綱數,可由下面等式計算:
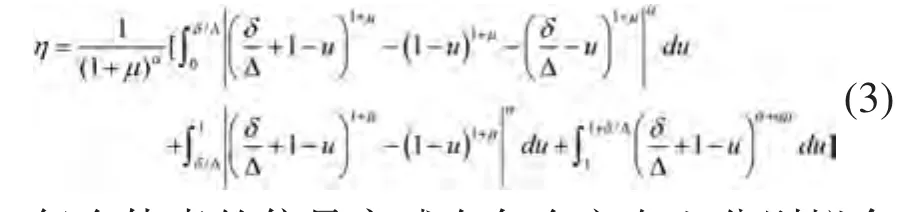
每個體素的信號衰減在各個方向上分別擬合公式(1),然后計算出各個方向上的平均參數值,使各向異性對參數結果的影響最小化。
2 基于FM模型的dMRl主要參數
FM模型假定組織內水分子擴散過程具有穩定的α、自相似的H和穩定的增量(步長)[14]。α表示Noah指數,是擴散梯度指數,與拉伸指數模型中的拉伸指數類似,是隨機擴散過程中增量波動的一個指標。當α=2時,增量符合高斯分布,當0<α<2時,增量則為Levy分布。H即赫斯特指數,用來描述分子軌跡的自相似性。β=αH,它決定了增量之間的相關性,當β=1時,FM的增量就是完全獨立的,當β<1,增量之間則呈負相關,反之β>1時,增量之間則呈正相關[19]。記憶參數μ=H-1/α ,當μ>0時,該過程中的增量則是正相關的,且表現為長期的依賴性(長時記憶,持久性),當μ<0時,增量則是負相關的,并且表現出短期的依賴性(短時記憶,瞬時性)[30]。在β<1、μ<0的情況下,擴散過程符合亞擴散模式,之前的研究已經證實,生物細胞內的水分子的運動存在亞擴散[3-4,6-7],這可能是由生物組織內水分子與黏滯擁擠的環境相互作用造成的。
3 FM模型MR成像技術要點及圖像后處理[31]
為了與FM模型匹配,同傳統的dMRI序列不同,該掃描序列運用特定的Stejskal-Tanner單次激發平面回波成像技術采集圖像,且在掃描的過程中,擴散梯度間隔時間(△)不固定,分別為27.5、40.0、55.5 ms,對于每一個△值,G0分別為15.67、19.68、24.73、 31.06、39.01、 49.00 mT/m,梯度持續時間=20.4 ms 保持不變。因此,在每一個方向的梯度上,一共會產生18個非零b值(151、239、377、595、938、1480、243、383、604、954、1504、2374、356、562、887、1399、2207、3482 s/mm2)。為了使擴散各向異性的影響最小化,分別在三個正交方向(x、y、z軸)上施加了擴散梯度場。另外也同時采集了12幅沒有擴散敏度(b=0)的圖像。其他采集參數為:TR 3800 ms,TE 110 ms,加速因子為2,FOV 24 cm×24 cm,分辨率128×128,層厚5 mm,激勵次數為2,總共掃描時間為8 min 42 s。常規MRI平掃和T1WI增強掃描所采集的圖像則用來做解剖定位及對比參照。在分析處理圖像之前,利用FSL (functional MRI of the brain's software library)工具[32]對頭動和渦流進行校正,然后再運用FM模型獲取反常擴散參數圖,傳統的ADC值則利用b=0和950 s/mm2計算得出,所有擬合程序均在Matlab (the Mathworks,Inc., Natick, MA)上進行。
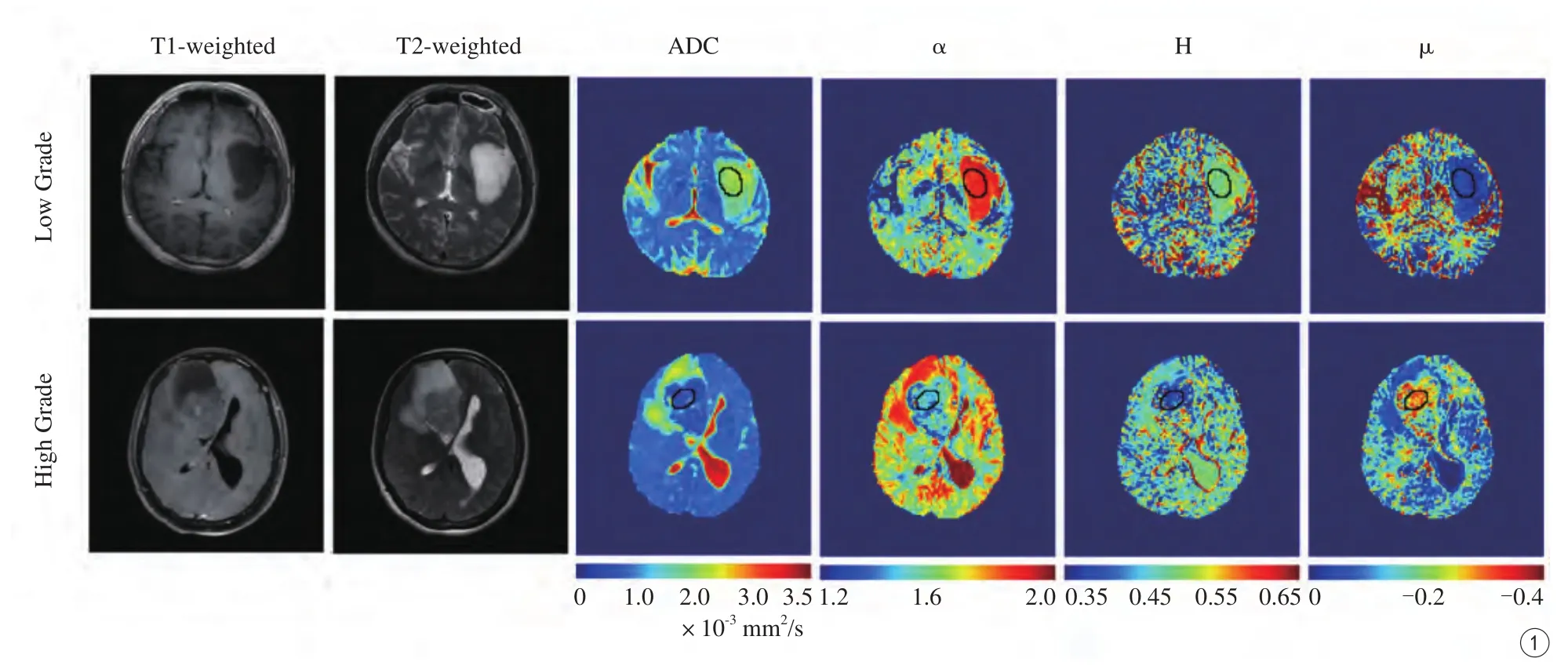
圖1 高、低級別膠質瘤常規MR圖像和相應層面的FM參數圖;參數圖中病灶實質部分內的小橢圓為選定的感興趣區Fig. 1 Conventional MR images and parameter maps of low- and high-grade gliomas. The ellipse areas in the parameter maps are ROIs of solid tumors.
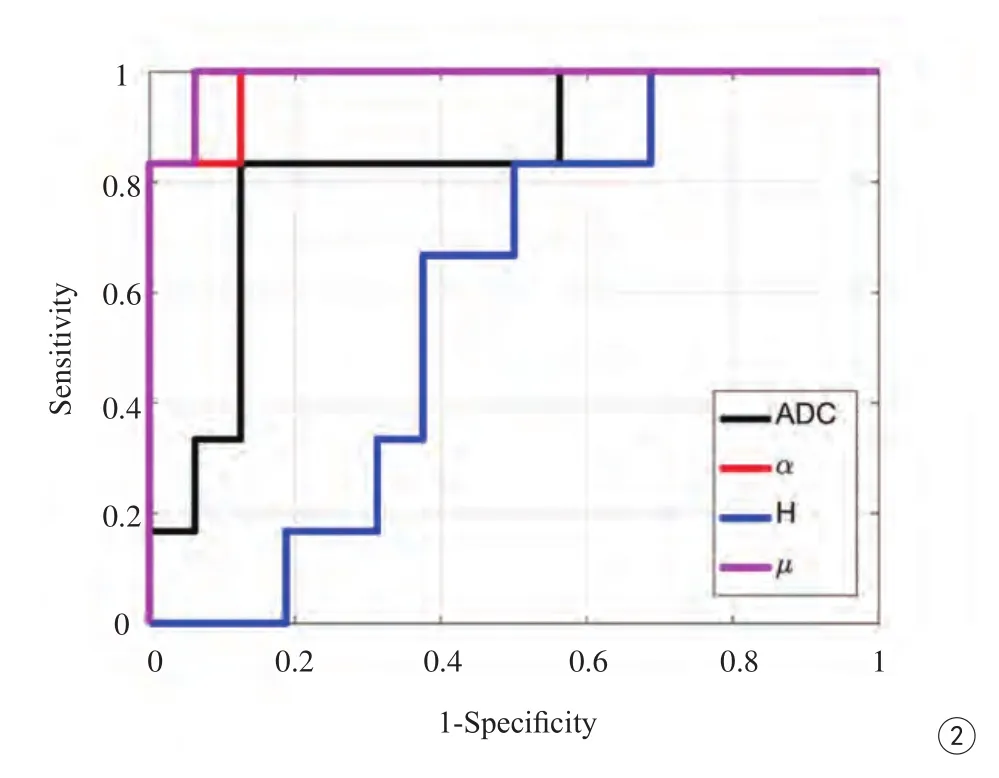
圖2 ADC、α、H及μ的ROC曲線圖;在鑒別高低級別膠質瘤的效能上α 、μ均比ADC值要高,而H值則較三者低Fig. 2 Receiver operating characteristic (ROC) curves of ADC, α , H and μ. α and μ show better performance as compared to ADC for distinguishing low- and high-grade gliomas, H exhibits the smallest AUC.
4 FM模型在顱內的初步應用
Fan等[19]在2015年首次將FM模型運用到活體人腦的MR擴散成像中,并從健康的志愿者中成功獲取了正常顱腦FM參數圖,這些參數在正常腦組織中表現出顯著的差異,比如在灰質,白質、腦脊液中。腦脊液的α和β值分別接近2.0和1.0,這說明了腦脊液中的水分子的擴散過程幾乎不受限制,近似于布朗運動,而從灰質到白質,α和β值分別表現出遞減的趨勢,說明了白質中反常擴散運動比灰質越加明顯。這些結果證明了腦實質內水分子反常擴散的異質性的存在,也表明了FM模型在在體dMRI中有較好的應用前景。
同樣基于這個模型,Xu等[31]利用配備有8通道頭線圈的GE 3T Discovery MR750磁共振掃描儀(GE Healthcare, Milwaukee, Wisconsin),對22例腦膠質瘤的患者進行了研究,比較分析病變與對側正常腦白質之間、高低級別膠質瘤之間的FM參數的差異,以及FM參數與常規擴散參數ADC(apparent diffusion coefficient)值對于鑒別高低級別膠質瘤的差異。結果顯示,FM參數值(α、μ、H)不僅可以很好地區別病變組織與正常組織(圖1),同時,α、μ值鑒別膠質瘤高低級別的效能都要比傳統的擴散系數ADC值要高(圖2)。這就證明了FM模型不僅可以更加準確無創地診斷腦內膠質瘤的高低級別,也為解釋腫瘤內部的微觀變化提供有力的影像依據,同時為臨床選擇有效治療方案、病情監視、指導預后具有潛在的價值。
5 不足與展望
雖然基于FM模型的dMRI已經在顱腦中得到了成功的應用,但是該模型也存在一定的局限性。首先,運用了單次激發平面回波成像,可能會導致圖像的失真和信號的丟失;盡管高效的梯度場和螺旋槳成像技術已經大大地減少了圖像的偽影,但偽影仍然可能存在,這會限制對生物組織的準確評價;其次,單次掃描時間和圖像后處理的時間還比較長,不利于該模型在其他部位及臨床中廣泛的應用;另外,目前有限的研究還沒有完全闡明該模型各個成像參數與病變組織病理改變之間的對應關系[31]。上述的不足與局限不僅說明該模型在技術層面仍有較大的拓展空間,而且應該有更多的、更大樣本量的關于FM模型的研究來解釋上面所提出的挑戰。總之,隨著MR成像技術的革新、FM模型的進一步優化和更多的關于該模型的研究,基于FM模型的dMRI必將為今后的科研與臨床帶來一個嶄新的未來。
[References]
[1] Torrey HC. Bloch equations with diffusion terms. Phys Rev, 1956,104(3): 563-565.
[2] Stejskal E, Tanner J. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys, 1965,42(1): 288-300.
[3] Golding I, Cox EC. Physical nature of bacterial cytoplasm. Phys Rev Lett, 2006, 96(9): 098102.
[4] Jeon JH, Tejedor V, Burov S, et al. In vivo anomalous diffusion and weak ergodicity breaking of lipid granules. Phys Rev Lett, 2011,106(4): 048103.
[5] Dix JA, Verkman A, Annu. Crowding effects on diffusion in solutions and cells. Rev Biophys, 2008, 37: 247-263.
[6] Lubelski A, Sokolov IM, Klafter J. Nonergodicity mimics inhomogeneity in single particle tracking. Phys Rev Lett, 2008,100(25): 250602.
[7] Bronstein I, Israel Y, Kepten E, et al. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys Rev Lett, 2009,103(1): 018102.
[8] Metzler R, Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys Rep, 2000, 339(1):1-77.
[9] Klemm A, Metzler R, Kimmich R. Diffusion on random-site percolation clusters: theory and NMR microscopy experiments with model objects. Phys Rev E Stat Nonlin Soft Matter Phys, 2002,65(2): 021112.
[10] Novikov DS, Fieremans E, Jensen JH, et al. Random walks with barriers. Nat Phys, 2011, 7(6): 508-514.
[11] Cherstvy AG, Metzler R. Nonergodicity, fluctuations, and criticality in heterogeneous diffusion processes. Phys Rev E Stat Nonlin Soft Matter Phys , 2014, 90(1): 012134.
[12] Cherstvy AG, Metzler R. Ergodicity breaking, ageing, and confinement in generalised diffusion processes with position and time dependent diffusivity. J Statist Mechan Theory Expe, 2015, (5):1502, 01554.
[13] Cherstvy AG, Chechkin AV, Metzler R. Particle invasion, survival,and non-ergodicity in 2D diffusion processes with space-dependent diffusivity. Soft Matter, 2014, 10(10): 1591-1601.
[14] Eliazar II, Shlesinger MF. Fractional motions. Phys Rep, 2013,527(2): 101-129.
[15] Magdziarz M, Weron A, Burnecki K, et al. Fractional brownian motion versus the continuous-time random walk: a simple test for subdiffusive dynamics. Phys Rev Lett, 2009, 103(18): 180602.
[16] Szymanski J, Weiss M. Elucidating the origin of anomalous diffusion in crowded fluids. Phys Rev Lett, 2009, 103(3): 38102.
[17] Weiss M. Single-particle tracking data reveal anticorrelated fractional brownian motion in crowded fluids. Phys Rev E Stat Nonlin Soft Matter Phys, 2013, 88(1): 010101.
[18] Ernst D, Hellmann M, K?hler J, et al. Fractional brownian motion in crowded fluids. Soft Matter, 2012, 8: 4886-4889.
[19] Fan Y, Gao JH. Fractional motion model for characterization of anomalous diffusion from NMR signals. Phys Rev E Stat Nonlin Soft Matter Phys, 2015, 92(1): 012707..
[20] De Santis S, Gabrielli A, Palombo M, et al. Non-gaussian diffusion imaging: a brief practical review. Magn Reson Imaging, 2011,29(10): 1410-1416.
[21] Niendorf T, Dijkhuizen RM, Norris DG, et al. Biexponential diffusion attenuation in various states of brain tissue: implications for diffusionweighted imaging. Magn Reson Med, 1996, 36(6): 847-857.[22] Mulkern RV, Gudbjartsson H, Westin CF, et al. Multi-component apparent diffusion coef ficients in human brain. NMR Biomed, 1999,12(1): 51-62.
[23] Bennett KM, Schmainda KM, Bennett RT, et al. Characterization of continuously distributed cortical water diffusion rates with a stretched-exponential model. Magn Reson Med, 2003, 50(4):727-734.
[24] Yablonskiy DA, Bretthorst GL, Ackerman JJ. Statistical model for diffusion attenuated MR signal. Magn Reson Med, 2003, 50(4):664-669.
[25] Jensen JH, Helpern JA, Ramani A, et al. Diffusional kurtosis imaging: the quanti fication of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med, 2005, 53(6):1432-1440.
[26] Magin RL, Abdullah O, Baleanu D, et al. Anomalous diffusion expressed through fractional order differential operators in the bloch–torrey equation. J Magn Reson, 2008, 190(2): 255-270.
[27] Cooke JM, Kalmykov YP, Coffey WT, et al. Langevin equation approach to diffusion magnetic resonance imaging. Phys Rev E Stat Nonlin Soft Matter Phys, 2009, 80(6): 61102.
[28] Zhou XJ, Gao Q, Abdullah O, et al. Studies of anomalous diffusion in the human brain using fractional order calculus. Magn Reson Med,2010, 63(3): 562-569.
[29] Ingo C, Magin RL, Colon-Perez L, et al. On Random walks and entropy in diffusion-weighted magnetic resonance imaging studies of neural tissue. Magn Reson Med, 2014, 71(2): 617-627.
[30] Burnecki K, Weron A. Fractional Lèvy Stable motion can model subdiffusive dynamics. Phys Rev E Stat Nonlin Soft Matter Phys,2010, 82(2): 021130.
[31] Xu B, Su L, Wang Z, et al. Anomalous diffusion in cerebral glioma assessed using a fractional motion model. Magn Reson Med, 2017.[Epub ahead of print]
[32] Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL.NeuroImage, 2004, 23(Suppl 1): S208-S219.
Initial application of fractional motion model in brain of anomalous diffusion
WANG Zhen-xiong, XU Bo-yan2, ZHU Wen-zhen1*
1Department of Radiology, Tongji Hospital Affiliated to Tongji Medical College of Huazhong University of Science and Technology, Wuhan 430030, China
2Magnetic Resonance Imaging Research Center of Peking University, Beijing 100871,China
*Zhu WZ, E-mail: zhuwenzhen8612@163.com
dMRI has been widely used in clinic, which is the only noninvasive method to research the diffusion processes in living tissue currently. The theory of traditional dMRI was based on the Brownian motion model, however, research has showed that the diffusion processes in crowded environments of biological cells are non-Brownian, also referred to as "anomalous diffusion". Several models have been proposed to explain anomalous diffusion phenomena in vivo and the fractional motion (FM) model is considered more appropriately among them. The model can not only re flect the anomalous diffusion of molecules in tissues but also provide rich information of subtle changes in organizational structure with its multiparameter (α,β, μ, H), thus guiding for disease diagnosis, treatment and prognosis. This article is aimed to review the imaging mechanism of FM model and initial application of FM model in brain of anomalous diffusion.
Diffusion magnetic resonance imaging; Anomalous diffusion; Brain
Received 16 Feb 2017, Accepted 18 Apr 2017
ACKNOWLEDGMENTSThis paper is funded by National Science Foundation of China (No.81570462).
國家自然科學基金項目(編號:81570462)
朱文珍,E-mail:zhuwenzhen8612@163.com
2017-02-16
接受日期:2017-04-18
R445.2;R651.1
A
10.12015/issn.1674-8034.2017.05.011
王振熊, 許博巖, 朱文珍. 分數化運動模型在顱腦反常擴散中的初步應用.磁共振成像, 2017, 8(5): 374-377.

