巧用Scratch作圖培養小學生計算思維策略

郭巍丹

隨著Scratch教學的深入開展，教師在教學中經常會遇到一些問題：學生躍躍欲試卻無從下手，學生反復調試卻效果不佳，學生學會了案例卻創意不足。分析這些現象的原因所在，深入思考Scratch教學的本質，筆者發現，Scratch圖形化指令直觀明了，學生可以很快掌握這些指令，編寫簡單的小程序。但隨著學習的深入，任務變得復雜，角色開始增多，每個角色的功能增加，用到的指令越來越多，程序也越來越復雜，這時就需要運用計算機科學的基礎概念去求解問題和設計系統，利用遞歸思維和啟發式推理來尋求解答，也就是如今所說的在Scratch教學中要培養小學生的計算思維。結合Scratch教學中發現的問題和小學生的認知水平，筆者認為利用Scratch作圖的創作過程可以有效培養小學生的分解、遞歸等算法思維及概括、推理等計算思維。

● 分析任務：由外到內逐層分解

充分理解案例、學會分析任務是解決任何編程問題的第一步。理解之后，可以做出一個大致的解決方案，然后將其劃分為多個主要任務進行突破，幾個主要的任務又可以各自作為大任務再分解成小任務進行解決，這樣的順序稱為由外到內逐層分解。在用Scratch作圖時，教師經常會用到這樣的分析方法，這種方法同樣也可以運用到其他類別的Scratch作品的創作中。

例如，學生拿到“蜘蛛網”案例時，雖然直觀上感覺對圖形非常熟悉，也知道這是一個特殊圖形，但由于缺乏計算思維的訓練，在編程時仍無從下手，而這正凸顯了動手編程前任務分析的重要性。在程序實現之前，教師要引導學生對圖形進行觀察，發現圖形生成具有的規律，幫助學生一層層地推理和分析。筆者以在Scratch中做出“蜘蛛網”圖形為例，引領學生一起分析，得出如下兩種圖形分解思路。

第一種（如上頁圖1）：從最外層分解，這個“蜘蛛網”圖形首先可以分成5個大的六邊形；再進一步分解，每個大六邊形又可以分解成6個大小一樣的正三角形，最終歸到一個基礎圖形“三角形”。只要能畫出這個最小的正三角形，通過變換就能得到最小的正六邊形，再通過變換將小六邊形邊長增加，就可以制作成一個“蜘蛛網”圖形。

第二種（如上頁圖2）：將這個“蜘蛛網”圖形分解成六個大小一致的大正三角形；每個大正三角形由5個邊長依次增加的小正三角形組成，最終也是歸到小正三角形上。只要先制作出這個小正三角形，就可以通過程序指令生成一個“蜘蛛網”圖形。

從案例中可以發現，對復雜問題由外到內逐層分解可以幫助學生化繁為簡，體驗從復雜問題到具體問題的分解過程，學生掌握了這種分析任務的切入口，找到了解決問題的方法，就會從無從下手發展到躍躍欲試。

● 程序實現：由內到外逐層遞歸

通過前面由外到內的逐層分析，能夠在復雜問題中分解出要解決的具體小任務。集中解決好復雜問題中的小問題，把各個細節問題解決好，再進行合理的組裝，就能由內到外一步步解決問題。因此，在這個程序實現過程中，教師要著眼于具體的小任務。

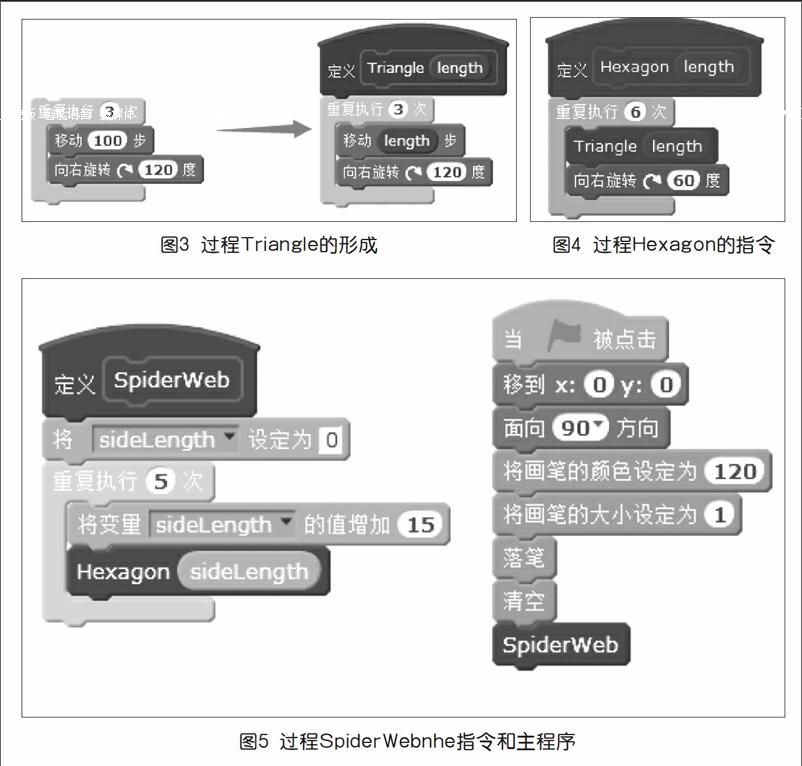
在繪制“蜘蛛網”的案例中提到了兩種分解過程，筆者在這里用第一種思路講解如何由內到外一層層編程，再結合問題分析結果。最內層的過程就是實現正三角形的繪制，學生很快能夠編寫出繪制正三角形的程序：重復執行3次移動數值（這里以100為例）和旋轉（120度）兩個指令。這就是解決任務中最內層的過程，命名為Triangle。但考慮到外層過程中，正三角形的邊長是要變化的，不能固定100，所以Triangle中必須還有一個自變量length（如圖3）。

第二層過程是實現每旋轉60度繪制一個正三角形直至一周。只要每旋轉60度，執行一次過程Triangle即可，將這個繪制正六邊形的過程命名為Hexagon，同樣要設置自變量length（如圖4）。

最外層過程是實現繪制5個依次增加邊長的六邊形。利用同樣的解決思路，重復執行5次Hexagon。由于每執行一次，變量length要增加一定的值，所以length需要用新的變量進行控制，將這個頂層的過程命名為SpiderWeb。主程序只要調用最外層過程SpiderWeb，就能繪制出精美的蜘蛛網了（具體代碼如上頁圖5）。

由內到外的程序實現過程，給學生編程提供了明確的線索，幫助學生理清任務與任務之間、問題與問題之間的邏輯關系。在整個編寫過程中，就如同提供了一步步的腳手架，通過用計算機自動繪制出這些神奇的圖形，讓學生感受到計算機程序設計的強大魅力。

● 定義過程：減少程序的漏洞

簡單是程序設計的目標，就像工廠里的流水生產線往往被劃分成若干個工位，每一個工位執行標準化、程序化的動作，這就是單一責任。在程序設計中，單一責任是指某個代碼的功能，應該保證只有單一、明確的執行任務。任務越單一，代碼越簡單，越簡單的代碼占用時間越少，漏洞越少，并且易于修改。當其他功能部分發生變化時，也能夠盡可能降低對其他組件的影響。在“蜘蛛網”的案例中，將每個分步都定義為一個過程（如圖6），每個過程只做單一的任務，如Triangle只負責繪制某一邊長的正三角形。

定義過程不僅有利于學生理清編程的思路，也方便程序的調試。在調試程序的過程中，可以將總目標分解成一層層由內向外的過程進行逐一調試。案例中可以先調試是否能畫出一個三角形，調試成功后，再調試是否能成功畫出六邊形。以此類推，直至成功。

● 應用拓展：從范例學習到個性創意

Scratch的教學本身就是“為了創作而教”，無論什么主題的作品都不能忽視自由創作。在繪制圖形的案例中，學生主要是學習了問題的分解與具體問題達成的邏輯，重在方法的剖析，而非圖形本身。這為學生走出范例進行個性化創作奠定了良好的基礎。

1.修改變量過程，變化效果

幾何圖形的變換千姿百態，但核心思想不變。在圖形繪制中只需要修改某一個變量（邊長、邊數、旋轉角度）或者修改過程中執行的命令，就可以帶來各種各樣的效果。當然，修改之前需要先有總體的架構，明確自己的目標圖形。例如，在學生學會繪制正三角形和正三角形變換得到的蜘蛛網案例后，可要求其自行設計繪制正方形，并將繪制正方形的過程作為底層過程函數，創作更加復雜的圖案（如上頁圖7）。

2.巧用問詢模塊，實現交互

在繪圖的創作過程中，有學生提出不要固定繪制的圖案，如上面案例中實現實時繪制6個花瓣、7個花瓣……只要將第三個過程函數的重復執行次數設為變量，并在主程序中加入問詢的指令（如上頁圖8），那么，當回答不同的數值時，count的值就會不同，調用過程函數Rotated Squares后的圖案也會發生變化（如圖9）。

3.設置畫筆性質，美化圖案

畫筆模塊中有多條與畫筆屬性相關的指令，學生將這些指令合理地添加到子程序中，就可以繪制出更加精美的圖案。例如，某學生在上面案例中的子程序Square中，每次執行就增加畫筆的顏色值，并在Rotated Squares子程序中恢復畫筆起始顏色，成功繪制出了色彩豐富的花瓣（如圖10）。

幾何圖形的創作周期和需要考慮的內容明顯小于一個好玩的游戲、動畫等互動性作品的創作，也正因為如此，學生發揮的創意可以很小，也可以很大。但是，無論是簡單修改變量還是顏色，通過不同邏輯的嵌套后，最后的成品都是豐富多彩的。這樣簡單的操作，卻能收獲豐富的即時的可視化的作品，能更加激發學生對邏輯的探究，并體驗到圖形繪制的趣味。

總之，由于Scratch軟件存在可視化編程環境、畫筆的多種性質、過程函數的方便調用，以及可以結合其他指令達到更多交互功能等優勢，使得Scratch作圖變得既有趣又簡單，大大激發了學生的創作激情。幾何圖形的創作并不能涵蓋Scratch軟件的所有功能指令。因此，Scratch作圖旨在培養學生的編程思維，而非Scratch指令的系統學習。筆者希望學生通過對Scratch作圖的學習，學會分析問題、體驗解決問題的方法，并將學習中滲透的計算思維運用到Scratch指令的學習中，為Scratch作品的創作提供解決問題的策略。endprint