三維隨機振動環境下MEMS加速度計輸出特性分析

孫麗艷，張 帥，李 鵬，張宏彬，陳東海

(北京航天控制儀器研究所，北京100039）

三維隨機振動環境下MEMS加速度計輸出特性分析

孫麗艷，張 帥，李 鵬，張宏彬，陳東海

(北京航天控制儀器研究所，北京100039）

對MEMS慣性測量單元進行了三維隨機振動試驗，初步探討了MEMS慣性測量單元在三維振動試驗條件下的故障模式：3個軸的MEMS加速度計均出現了零位偏移，該現象在單軸振動試驗環境中并沒有出現。從理論和仿真分析了該現象產生的機理，提出了解決辦法并通過了試驗驗證。結果表明：三維振動比單軸的振動更能接近真實的振動環境，結構被激發的模態更豐富。通過采取措施，減小了加速度計的零偏值，從9.4m/s2降至1.97m/s2。

三維隨機振動；加速度計零位偏移；結構模態

Abstract：Performance of MEMS inertial measurement unit is tested in three?axis random vibration environ?ment.Failure mode of the IMU in the three?axis random vibration environment is discussed firstly and it didn't occur in the one?axis vibration environment.The cause of the failure is analyzed in theory and simulation.The way to decrease the failure mode is produced and validated by experiment.The result indicates that three?axis vibration environment is more authentic than one?axis，which can excited more modes of the structure.Zero bias of MEMS accelerometer is reduced after our meas?ure：9.4m/s2to 1.97m/s2.

Key words：three?axis random vibration;drift of the accelerometer;structure mode

0 引言

振動環境在本質上來講都是多軸的，用單軸振動試驗來近似等效多軸振動試驗這種方法雖然簡單，但有一定局限性，兩者并不能簡單地等效［1］。首先，單軸振動無法模擬多自由度耦合的振動環境，使得系統在真實振動環境中的故障模式難以復現［2?4］。其次，多軸振動激勵的耦合效應十分復雜，與單軸振動的差別很難做出定量的估計，即使加大量級也不能替代多軸振動環境［1］。

三維隨機振動試驗是指3個振動臺同時激勵試驗件，并按試驗條件控制激勵系統界面的運動響應，使試驗件做三維空間運動以考核試驗件的力學性能及可靠性，其主要目的是用試驗的方法再現試驗件所處的真實環境［3］。目前，國內外在多維試驗技術方面也開展了相關研究，通過運用多維結構、多維控制等技術實現了同一位置的不同方向上施加各自不同量級的振動激勵，更加真實地模擬振動環境，更有效地暴露產品的潛在缺陷［5?7］。

隨著三維隨機振動試驗技術的發展，越來越多的MEMS產品選擇多維隨機振動試驗進行性能考核，由此也暴露出了更多的輸出特性。現有文獻報道的三維振動的分析大都是針對某一具體結構件進行分析，本文針對小體積的MEMS慣性測量單元進行了三維隨機振動試驗，分別在水平和垂直方向各使用一振動臺。通過運用多維解耦、多維控制技術［2］等，可以更加真實地模擬振動環境。試驗結果表明：多維振動試驗能夠更有效地暴露產品潛在的缺陷。

1 機理分析

1.1 MEMS慣性測量單元

MEMS慣性測量單元集成了3個MEMS加速度計及3個MEMS陀螺儀，可以提供載體的角速率及線加速度，通過積分運算可以得出載體的姿態角，實現慣性導航。本次進行三維振動試驗的MEMS慣性測量單元結構為方形，由箱體和上蓋組成。系統未施加減振器，與載體剛性連接，如圖1所示。

圖1 MEMS慣性測量單元示意圖Fig.1 Sketch of MEMS inertial measurement unit

1.2 三維振動機理

未施加減振器的慣性測量單元其力學特性屬于線性系統，對于線性結構來說，單軸或三軸加載下結構的模態(自振頻率及陣型）是不變的，但振動響應是有區別的。單軸振動時，單方向的結構響應是由該方向的振動載荷引起的；而三軸振動時，單方向的結構響應是3個方向振動載荷共同作用的結果。三軸激勵的動力學方程可表示為［1］：

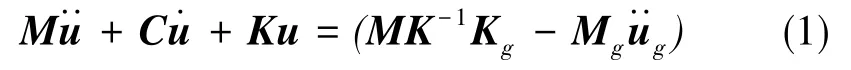
M、C、K分別表示系統非約束自由度的質量矩陣、阻尼矩陣和剛度矩陣；Mg、Kg分別表示系統約束自由度的n×m階質量矩陣、剛度矩陣；和u分別表示非約束自由度的加速度、速度和位移向量；表示施加在約束自由度上的激勵加速度向量。

根據結構的特征方程，有：

可計算出結構的自振頻率ω和陣型φ，從而可推導出結構在某方向的響應功率譜密度Sk(ω）。因此三軸振動時，其響應的功率譜密度為［1］：

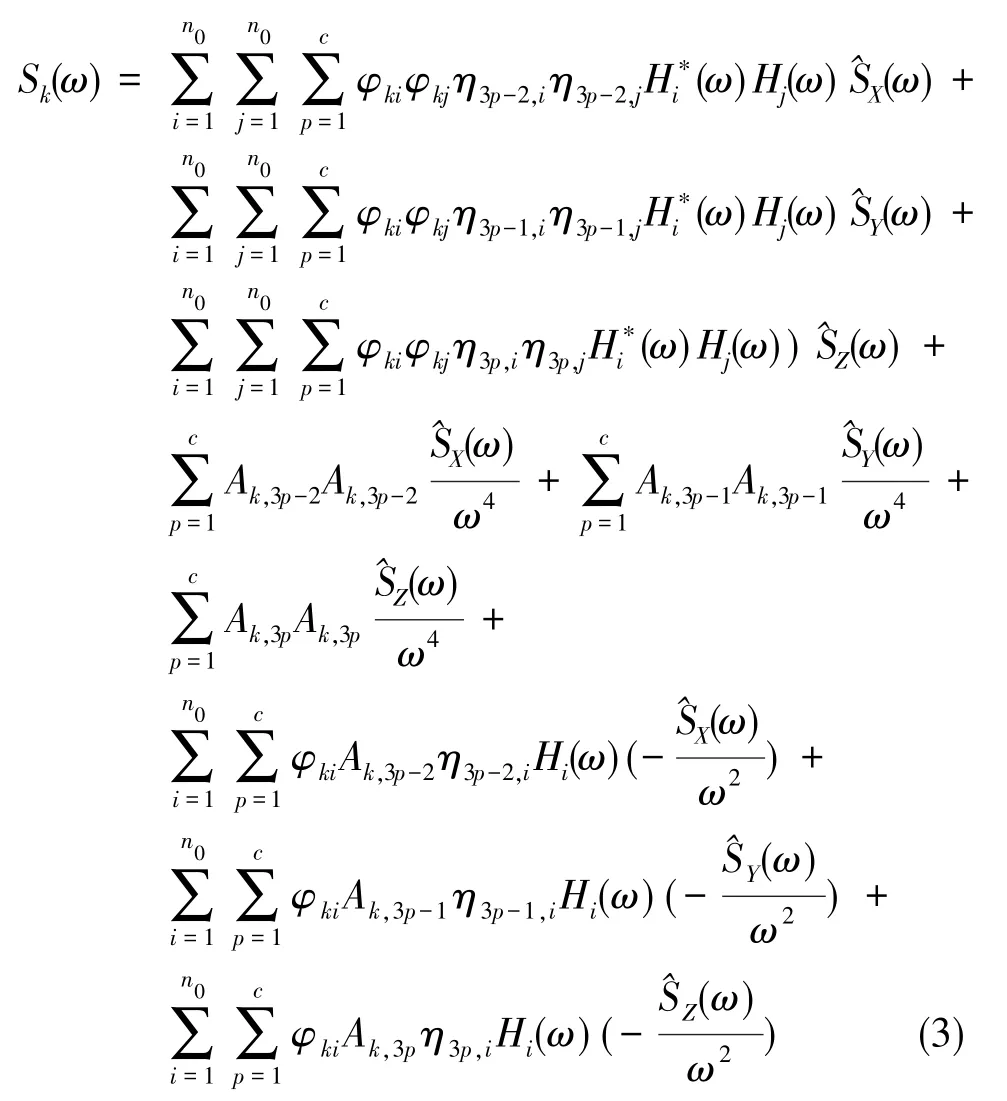
其中，A＝－K－1Kg；為單自由度系統位移的頻響函數；為Hi(ω）的共軛；為基礎激勵功率譜；為振型參與系數，為廣義質量。

從以上分析可知，單軸、三軸加載下響應的區別主要是對模態的不同激發效果帶來的。單軸加載時，單方向的響應僅包含了加載軸方向的模態信息；X軸、Y軸、Z軸同時加載時，單方向的響應信息同時體現了3個加載軸的模態信息。各軸振動對響應的影響由載荷的大小和陣型系數確定，陣型系數與結構的剛度有關。

1.3 系統模態分析

為考核本體剛度，對MEMS慣組的簡化模型進行了模態分析，前3階模態的本征頻率如表1所示。由于系統采用的是簡化的模型，各參數設置為理論值，仿真結果只能定性說明問題。3個MEMS加速度計分別安裝在箱體底部和正交的兩側壁上，加速度計安裝位置處的前3階的陣型如圖2所示。第1階陣型沿X向移動，第2階陣型沿Y向移動，第3階陣型沿Z向移動。其中，各向位移在另外兩方向均存在分量。從圖2可以看出，該1階陣型X向、Y向激勵引起的響應在Z向的分量最大，陣型參與系數最大。因此，Z向加速度計的響應，X向、Y向激勵的作用是不可忽略的。

表1 簡化模型后系統模態的前3階頻率Table 1 Frequency of the first three modes

圖2 箱體3階陣型Fig.2 The first three modes of the body

以Z向MEMS加速度計的響應為例，該方向的響應既包含了Z向激勵激發的第3階模態的信息，又包含了X向、Y向激勵激發的1階、2階陣型在Z向的分量。其中，Z向激勵是動態的，響應信息在正負向隨機變化，使均值在零位附近動態變化。但是，X向、Y向激勵激發的1階、2階陣型在Z向的分量并不是在零位附近變化，該分量的大小由陣型系數及陣型的振動幅值確定。當外加振動激勵停止后，Z向MEMS加速度計的響應回到零位。

其余兩軸加速度計響應產生零位偏移原理與之相同。由以上分析可知，三軸振動會出現單軸振動沒有出現的現象，是由單軸、三軸加載對模態不同的激發效果引起的。

2 試驗系統

將MEMS慣性測量單元通過振動工裝固定在三維振動臺面上，如圖3所示。各通道控制參數確定完成后，輸入各軸振動譜形，如圖4所示。為驗證量級的大小對系統結構響應有影響，選用兩種不同的譜形：譜形1和譜形2。兩種譜形X向的均方根加速度值均為8.42g；譜形1的Y向、Z向均方根加速度值為8.34g；譜形2的Y向、Z向均方根加速度值為10.6g。振動過程中MEMS慣組通電采集數據，譜形1振動結果如表2所示，譜形2振動結果如表3所示。

圖3 三維振動試驗系統示意圖Fig.3 Experiment system of the three?axis random vibration

圖4 兩種振動譜形Fig.4 The two different spectral

表2 譜形1振動條件下加速度計數據對比Table 2 Output of the accelerometer under the first vibration spectral

表3 譜型2振動條件下加速度計數據對比Table 3 Output of the accelerometer under the second vibration spectral

從表2、表3可以看出，3個方向的MEMS加速度計均出現了零位偏移，尤其是Z向MEMS加速度計零偏的量值達0.9g，振動停止后MEMS加速度計的輸出又回到零位。該現象在單軸振動過程中沒有出現，且通過單軸振動加大量級的方法現象沒有復現。由上述模態仿真得出結論：Z向加速度計的響應除去Z向激勵產生的響應外，X向、Y向激勵同時都對Z向響應有很大的貢獻。譜形2的振動結果表明：3個加速度計的零偏比譜形1的要大。這進一步說明了加速度計的響應與外加激勵載荷的量級有關。

系統結構的響應除與激勵載荷的量級有關外，與系統的結構剛度也有關。為減小加速度計的零偏，采用硅橡膠加固，改變系統原有剛度。用硅橡膠將加速度計安裝進一步加固，加固完成后再次做三維振動試驗，試驗圖譜與第一次試驗相同。試驗結果如表4所示，此次僅給出MEMS加速度計振中的數據作為對比。從表4可以看出，經過加固后，加速度計的零偏明顯比未加固狀態的小，Z向加速度計的零偏由9.4m/s2降至 1.97m/s2。

表4 MEMS慣組第二次三維振動試驗數據Table 4 The second experiment data of the inertial measurement unit

3 結論

分析了三維振動的原理，給出了三維振動條件下，結構體的響應譜密度理論計算公式。結合仿真分析，進一步定性分析了三維振動條件下，各方向結構模態的相互作用，驗證了三維振動能夠激發更多的結構模態。最終通過試驗驗證了上述分析結果，并通過加固的方式減小了加速度計的零偏值，從9.4m/s2降至1.97m/s2。

[1]陳潁,朱長春,李春枝,等.典型結構在單、多軸隨機振動下的動力學特性對比研究[J].振動工程學報,2009,22(4）:386?390.CHEN Ying,ZHU Chang?chun,LIChun?zhi,et al.Comparison of dynamic characteristics of a typical structure under single?axial and multi?axial random vibration loads[J].Journal of Vibration Engineering,2009,22(4）:386?390.

[2]陳立偉,衛國.多維隨機振動試驗條件制定方法研究[J].強度與環境,2010,37(6）:1?6.CHEN Li?wei,WEI Guo.Methodology of design conditions for multi?axis random vibration test[J].Structure and Envi?ronment Engineering,2010,37(6）:1?6.

[3]吳家駒,榮克林.多維振動環境試驗方法[J].導彈與航天運載技術,2003(4）:27?32.WU Jia?ju,RONG Ke?lin.Multi?dimensional vibration en?vironmental test method[J].Missiles and Space Vehicles,2003(4）:27?32.

[4]陳潁,朱長春,李春枝,等.某結構的多軸隨機振動實驗研究[J].實驗力學,2009,24(1）:35?41.CHEN Ying,ZHU Chang?chun,LI Chun?zhi,et al.Mul?tiaxial random vibration research of a typical structure[J].Journal of Experimental Mechanics,2009,24(1）:35?41.

[5]王曉飛,王剛,高貴福,等.一種系統級多維振動試驗技術[J].航天器環境工程,2014,31(5）:516?521.WANG Xiao?fei,WANG Gang,GAO Gui?fu,et al.A sys?tem?level multi?dimensional vibration test technology[J].SpacecraftEnvironment Engineering,2014,31(5）:516?521.

[6]Chang K Y,Frydman A M.Three?dimensional random vi?bration testing definition and simulation[C].PIES,1990:129?139.

[7]Underwood M A,Keller T.Recent system developments for multi?actuator vibration control[J].Sound and Vibration,2001,35(2）:52?58.

Performance of MEMS Accelerometer in Three?axis Random Vibration Environment

SUN Li?yan,ZHANG Shuai,LI Peng,ZHANG Hong?bin,CHEN Dong?hai
(Beijing Institute of Aerospace Control Devices,Beijing 100039）

U666.1

A

1674?5558(2017）02?01276

10.3969/j.issn.1674?5558.2017.05.010

2016?05?05

孫麗艷，女，博士，高級工程師，研究方向為捷聯慣性導航系統。