激勵頻率對扭轉模態磁致伸縮導波檢測性能影響

李志農， 孟寧， 龍盛蓉

(南昌航空大學 無損檢測技術教育部重點實驗室， 江西 南昌 330063)

激勵頻率對扭轉模態磁致伸縮導波檢測性能影響

李志農， 孟寧， 龍盛蓉

(南昌航空大學 無損檢測技術教育部重點實驗室， 江西 南昌 330063)

在綜合考慮力-磁-聲的多個物理場耦合的基礎上，通過采用有限元數值仿真方法模擬扭轉模態磁致伸縮導波對鐵磁性管道的檢測，研究激勵電流頻率對T模態導波檢測效果的影響，并通過實驗給予驗證.結果表明：實驗研究數據與仿真計算結果具有相同的變化趨勢且存在一個最優頻率；激勵頻率對檢測效果有著明顯的影響，通過調整激勵頻率能夠使扭轉模態導波幅值最大，實現磁致伸縮導波檢測性能的優化.

超聲導波； 扭轉模態； 磁致伸縮效應； 激勵頻率； 導波檢測； 有限元仿真

Abstract： On the basis of considering the coupling of stress-magneto-acoustic multiple physical fields， the finite element numerical simulation method was used to simulate the torsional mode of magnetostrictive guided wave on the detection of ferromagnetic pipe. The effect of excitation current frequency on the guided wave detection of T mode was studied. The experiment results show that the numerical simulation and experiment test have very good consistency. The excitation frequency has a significant effect on the detection effect， and the amplitude of the torsional mode guided wave can be maximized by adjusting the excitation frequency, which can realize the optimization of the performance of the magnetostrictive guided wave detection.

Keywords： ultrasonic guided wave; torsional mode; magnetostrictive effect; excitation frequency; guided wave detection; finite element simulation

超聲導波檢測技術具有速度快、檢測距離長，以及能一次性完成對整個工件檢測等優勢，廣泛應用于管道檢測中.管道中導波的傳播方式主要有縱向模態L(n，m)、扭轉模態T(n，m)、彎曲模態F(n，m)[1].縱向模態傳播速度快、激發方式簡單，通常用于管道的周向裂紋的檢測中，然而，該模態導波對縱向裂紋并不夠敏感.與縱向模態相比，扭轉模態的傳播特性具有非頻散特點，且在傳播過程中能量衰減較小，不受管道中液體的影響[2].在現有研究中，對縱向模態的理論研究、仿真和實驗分析較多.龍盛蓉[3]對縱向磁致伸縮導波傳感器進行了有限元模擬仿真，對其可能的影響因素做了細致研究，并加以實驗驗證.Ludwig等[4]開發了包括磁致伸縮的超聲導波有限元模型，但沒有針對實驗進行驗證，也沒有包括從實際測量導出的物理參數.在扭轉模態方面，何存富等[5-6]基于壓電式傳感器對扭轉模態導波管道缺陷檢測進行仿真模擬，并對充水管道缺陷進行實驗研究.Kwun等[7]和Kim等[8]研制了基于磁致伸縮效應的磁致伸縮傳感器，實現在單層鋼管中激勵出T(0，1)模態并進行了缺陷檢測.本文在前人研究基礎上，運用有限元仿真方法對管道中扭轉模態導波的激勵情況進行數值模擬，并結合仿真模擬和實驗結果數據，分析激勵電流頻率對扭轉導波回波信號的影響.

1 扭轉模態磁致伸縮導波檢測原理

1.1磁致伸縮導波激勵傳感器檢測原理

導波的激勵過程是將電磁能轉變為彈性能，其中，彈性波是由激勵線圈產生的交變磁場在管道中激發出的.若在線圈中施加的激勵電流密度為J0，則產生的動態磁場本構方程[9]可以表示為

2A-μσ=-μ(Js+J0).

本構方程的動態組件可以由線性項近似表示，應變和磁場[10-11]可以表示為

式(2)中：SH為6×6的彈性矩陣；μσ為3×3的磁導率矩陣；σ為應力；SHσ為管道中應力所產生的應變；dHd為磁致伸縮效應所產生的外加應變.d為rθz坐標系下6×3的磁致伸縮系數矩陣，可表示為

1.2扭轉模態導波激勵傳感器結構

(a) 動態磁場結構 (b) 靜態磁場結構圖1 扭轉模態磁致伸縮導波傳感器結構Fig.1 Sensor structure of torsional mode magnetostrictive guided wave

扭轉模態磁致伸縮導波激勵傳感器結構，如圖1所示.用通電流的螺線圈繞管壁纏繞來產生動態激勵磁場，如圖1(a)所示;而對貼于管道外側的矩形鎳片沿長度方向進行磁化，使其處在偏置靜態磁場的周向磁化狀態下，如圖1(b)所示.依據Wiedemann效應，待檢測工件中材料介質質點受到由激勵線圈產生的沿管道軸向的磁致伸縮力，以及由偏置靜態磁場產生的沿管道周向的磁致伸縮力的共同影響，即可形成扭轉模態的磁致伸縮導波[3].

2 有限元模型仿真及結果分析

2.1仿真模型建立

對鐵磁性管道的數值模擬仿真是通過有限元軟件COMSOL Multiphysics實現的，幾何模型主要有交變線圈、鋼管、鎳帶和空氣等4個部分.整個管道扭轉模態磁致伸縮導波激勵模型的建立過程，包括模型各部分尺寸大小的選擇、添加材料屬性、邊界條件的定義，以及設置計算時間和網格劃分.這些因素的選取和設定對仿真計算結果的準確性和計算效率都有非常大的影響.因此，在保證計算精度和完整性的基礎上，將管道仿真模型的長度設置為100 mm，外徑為48 mm，壁厚為4 mm，激勵線圈匝數為40匝，激發導波的頻率選擇為120 kHz.管道材料屬性為鐵磁性，如表1所示.表1中：E為楊氏模量；υ為泊松比；ρ為密度；σ為電導率；λs為飽和磁致伸縮量；Ms為飽和磁化強度.

表1 磁致伸縮材料特性Tab.1 Magnetostrictive material characteristics

模型所加載的激勵信號選用漢寧窗調制的6個周期正弦信號，有

式(4)中：I為電流大小；f為激勵頻率.

圖2 仿真模型網格劃分Fig.2 Mesh devision of simulation model

COMSOL Multiphysics是以有限元法為基礎的多物理場仿真軟件，主要用于解決多個物理場耦合作用下的仿真模擬問題.管道磁致伸縮扭轉模態導波激勵模型是利用COMSOL Multiphysics中電磁學模塊及固體力學兩部分進行耦合分析.在電磁學分析部分，建立管道三維模型并劃分網格，計算激勵端鎳帶產生的靜態偏置磁場的值，同時利用式(1)建立動態磁場模型.在建立的動態磁場模型上，由式(2)求解激勵磁場引起的磁致伸縮應變，并把該應變作為輸入，加載到激勵線圈下方的管道區域，計算在該機理下產生的位移場[9].網格劃分后的模型,如圖2所示.

2.2仿真求解分析

通過仿真求解計算，分析在管道中激勵纏繞線圈產生的動態磁場的方向.取有限元管道模型中靠近線圈的任一質點為研究對象，該質點在交變磁場下的磁通密度(T)的一維圖像,如圖3所示.根據右手定則可以判定，繞管壁激勵線圈產生的磁場應沿x軸方向分布.由圖3可知：在沿管道軸向x軸方向通過質點的磁通密度最大，而沿y軸方向和z軸方向幾乎為0，符合磁場產生規律.因此，由線圈激勵出的動態磁場是沿管道軸向分布的.

管壁中由激勵線圈和周向磁化鎳帶產生的合成磁場的方向，如圖4所示.因為由鎳帶形成的周向偏置磁場遠大于線圈產生的交變軸向磁場，并且由于鎳帶處于線圈與管壁的中間位置(圖2)阻礙了交變磁場對管壁的磁化，所以最終動態磁場和靜態磁場的耦合作用只對管壁形成周向磁化.

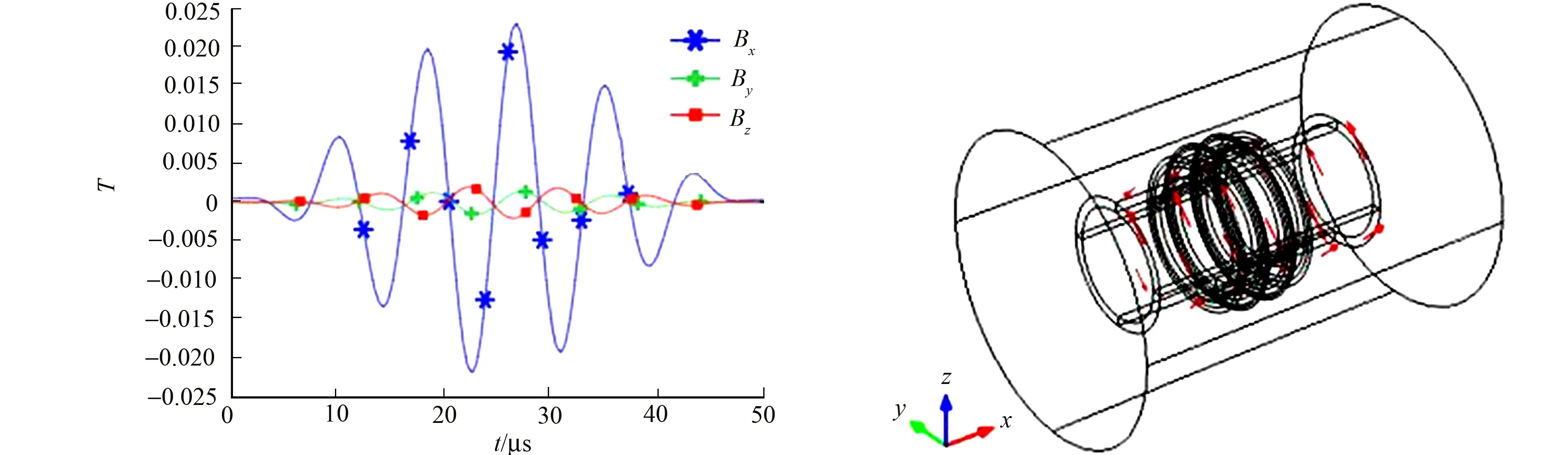
圖3 交變磁場質點磁通密度 圖4 耦合磁化條件下磁場分布圖Fig.3 Particle magnetic flux density in alternating magnetic field Fig.4 Magnetic field distribution under coupled magnetization

其次,為了研究管道中質點振動位移情況，在模型中鎳帶正下方管壁中心，約距離管道表面2 mm處取點(100，0，24)，仿真計算該點處管壁自身的磁致伸縮位移(Δ)，其結果如圖5，6所示.

由圖5,6可知：管壁中質點振動位移的周向分量(Δy)值為1.5×10-14mm，其數值比軸向位移分量(Δx)高出一個數量級.因此,可以確定該激勵模型產生的導波符合鐵磁性材料扭轉模態導波的傳播特性，即以周向振動為主，產生的波沿管道軸向傳播，傳播方向與質點振動方向相垂直.這說明通過該仿真分析能夠得到由力磁聲多場耦合產生的應變，能夠真實反映扭轉模態磁致伸縮導波.

圖5 質點周向位移與時間的關系 圖6 質點軸向位移與時間的關系Fig.5 Relationship between circumferential displacement of particle and time Fig.6 Relationship between axial displacement of particle and time

圖7 激勵電流頻率對質點振動位移的影響Fig.7 Influence of exciting current frequency on vibration displacement of particle

3 激勵電流頻率的影響

3.1數值計算分析

在上述建立的激勵仿真模型的基礎上，給交變線圈分別加載 60～160 kHz 不同頻率的電流，仿真計算分析交變線圈中激勵電流頻率對T模態導波檢測信號的影響.當激勵線圈電流頻率為 60～160 kHz 時，分別計算管道(100，0，24)處質點的磁致伸縮振動位移分量(Δy)，如圖7所示.

由圖7可知：當激勵頻率小于120 kHz時，隨著激勵電流頻率的增大，磁致伸縮振動周期與幅值均增大；當激勵頻率為120 kHz時，扭轉導波磁致伸縮振動幅值達到最大；但當交流線圈激勵電流頻率超過120 kHz時，隨著頻率的增大，質點的磁致伸縮振幅逐漸減小.說明激勵頻率對導波激勵信號強度有影響，存在一個最優激勵頻率,使產生的導波信號最好.

圖8 磁致伸縮扭轉導波實驗裝置示意圖Fig.8 Experiment equipment diagram of torsional magnetostrictive guided wave

3.2實驗驗證

為了驗證上述仿真分析的正確性，搭建管道磁致伸縮扭轉導波檢測實驗平臺，如圖8所示.磁致伸縮扭轉導波傳感器的激勵裝置放置在距離管端的550 mm處，接收裝置放置在距離管道同一端的1 180 mm處.通過信號發生器給予的激勵信號經過功率放大器后，輸入激勵線圈進行扭轉導波的激勵，產生的導波經過接收裝置產生相應感應的電壓信號，最后輸出到計算機上顯示.實驗使用的磁致伸縮導波傳感器參數：鎳帶尺寸為150.0 mm×30.0 mm×0.2 mm；激勵線圈匝數為40匝；激勵線圈漆飽線直徑為0.52 mm；接收線圈匝數為200匝；接收線圈漆飽線的直徑為0.21 mm；管道長度、內徑、外徑分別為3 200，44，48 mm.除管道長度外，磁化鎳帶和動態激勵線圈的尺寸參數與仿真模型一致.

給線圈施加6個周期的激勵信號，保持激勵電流強度為10 A，分別給交變線圈加載頻率為60，80，100，120，140，160 kHz 的激勵電流，采集得到的導波檢測回波信號,如圖9所示.圖9(a)中：A為幅值；加載頻率為60 kHz得到的波形，標注的回波1為空間干擾波，2為首次到達波，3，4，5均為端部反射波.

根據首次到達波和端部反射波3進行導波波速計算，從圖9中讀出首次到達波時刻為273 μs，端部回波信號3位于為613 μs處，則計算得到波速為3 235 m·s-1.與理論扭轉導波波速3 200 m·s-1的相對誤差很小，可知激勵得到的導波為扭轉模態導波.

(a) f=60 kHz (b) f=80 kHz

(c) f=100 kHz (d) f=120 kHz

(e) f=140 kHz (f) f=160 kHz圖9 不同激勵頻率下磁致伸縮扭轉導波Fig.9 Torsional magnetostrictive guided wave under different excitation frequency

由于在實驗中不能通過質點振動位移的方法進行研究，所以采用對回波信號峰值的分析方法確定電流激勵頻率對導波強度的影響，從而確定合適的檢測頻率.實驗中選取了回波信號中首次界面回波，并以其峰值Vp-p作為判斷標準，如圖9(a)中標注所示.

分別提取仿真結果中不同激勵頻率下磁致伸縮振動幅值的最大值點(Δmax)，與實驗結果中不同激勵頻率下回波信號的峰值(U)，繪制的關系圖如圖10所示.

由圖10(b)可知：不同的激勵頻率產生的回波信號峰值是不同的，在f=120 kHz時，扭轉導波的回

(a) 仿真導波振動幅值的最大值 (b) 實驗導波峰值圖10 不同頻率下實驗結果與仿真結果對比圖Fig.10 Comparison chart of experimental results and simulation results

波信號峰值達到最大，此結論與仿真計算結果(圖10(a))中的變化規律相一致.由此可見，在保持激勵電流大小一定的情況下，選擇不同的信號激勵頻率對于磁致伸縮傳感器的性能是有影響的，且存在一個最優激勵頻率使導波檢測信號最好.

4 結論

根據磁致伸縮導波傳感器檢測方程，在研究扭轉模態磁致伸縮導波激勵傳感器結構的基礎上，采用有限元軟件建立了管道磁致伸縮扭轉模態導波激勵過程的檢測仿真模型，并根據分析質點振動情況驗證了該激勵模型激發出的導波符合扭轉模態導波的特性.

另外，通過仿真模擬和實驗研究在不同激勵電流頻率下對T模態導波強度的影響情況，說明激勵頻率對導波激勵信號強度有影響，存在一個最優激勵頻率使扭轉模態導波幅值最大，檢測效果較好.該模型結合仿真和實驗對扭轉導波的激勵過程進行綜合分析，可為磁致伸縮扭轉導波傳感器的設計研究提供幫助.

[1] ROSE J L.Ultrasonic waves in solid media[M].Cambridge:Cambridge University Press，1999:154-163.

[2] KIM Y G，MOON H S，PARK K J，etal.Generating and detecting torsional guided waves using magnetostrictive sensors of crossed coils[J]．Ndt and E International,2011,44(2):145-151.

[3] 龍盛蓉.鐵磁性管道磁致伸縮導波檢測機理及傳播特性研究[D].南昌:南昌大學,2014:33-34.

[4] LUDWIG R，DAI X W.Numerical simulation of electromagnetic acoustic transducer in the time domain[J].J Appl Phys，1991，69(1):89-98.

[5] 何存富，李偉，吳斌.扭轉模態導波檢測管道縱向缺陷的數值模擬[J].北京工業大學學報，2007，33(10):1009-1013.

[6] 劉增華，吳斌，何存富，等.扭轉模態在充水管道缺陷檢測的實驗研究[J].儀器儀表學報，2006，27(6):1587-1589.

[7] KWUN H，KIM S Y，LIGHT G M.Long-range guide dwave inspection of structures using the magnetostrictive sensor[J].Journal of the Korean Society for Nondestructive Testing，2001，21(4):383-390.

[8] KIM Y Y，PARK C，CHO S H，etal.Torsional wave experiments with a new magnetostrictive transducer configuration[J].Journal of the Acoustical Society of America，2005，117(4):3459-3468.

[9] 孫鵬飛，武新軍，從明.磁致伸縮縱向導波管道檢測數值建模與分析[J].儀器儀表學報,2015,36(6):1251-1255.

[10] RIBICHINI R,CEGLA F,NAGY P B,etal.Quantitative modeling of the transduction of electromagnetic acoustic transducers operating on ferromagnetic media[J].IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2010,57(12):2808-2817.

[11] 王亞午.電磁超聲換能器多場耦合分析及實驗研究[D].武漢:湖北工業大學,2015:41-47.

(責任編輯： 黃仲一英文審校： 崔長彩)

InfluenceofExcitationFrequencyonDetectionPerformanceofTorsionalModeMagnetostrictiveGuidedWave

LI Zhinong， MENG Ning， LONG Shengrong

(Key Laboratory of Nondestructive Testing of Ministry of Education, Nanchang Hangkong University， Nanchang 330063)

10.11830/ISSN.1000-5013.201610030

2016-10-24

李志農(1966-)，男，教授，博士，主要從事智能檢測方面的研究.E-mail:lizhinong@tsinghua.org.cn.

國家重點研發計劃項目(2016YFF0203000)； 國家自然科學基金資助項目(51261024， 51675258)； 江西省教育廳科學技術研究項目(GJJ150699)； 南昌航空大學無損檢測技術教育部重點實驗室開放基金資助項目(ZD201429003)； 南昌航空大學博士科研啟動項目(EA201508008)

TB 512

A

1000-5013(2017)05-0632-06