基于復擺法的彈藥質偏測量及精度分析

劉永付，張心明，李俊燁，王德民，尹延路

（1.中國人民解放軍63867部隊，白城 137000；2.長春理工大學 機電工程學院，長春 130022）

基于復擺法的彈藥質偏測量及精度分析

劉永付1，張心明2，李俊燁2，王德民2，尹延路2

（1.中國人民解放軍63867部隊，白城 137000；2.長春理工大學 機電工程學院，長春 130022）

彈藥是武器裝備系統中的重要的組成部分，彈藥的質心位置會對彈藥飛行穩定性和飛行速度產生重要影響；彈藥的偏心位置對彈藥的飛行軌道有著決定性的作用，偏心將直接影響彈藥的目標命中概率，這些靜態參數對彈藥的性能具有重要意義。基于已有的復擺理論和結構基礎對質偏的復擺測量法進行研究，使得質偏的計算更加簡便，便于測試和計量，為質偏的測量提供了理論依據。

復擺法；測量；測試誤差；精度分析

1 測試系統結構及測試原理

復擺也稱為物理擺，復擺與單擺相比區別在于復擺的形狀為不規則剛體，轉軸與質心相交，在復擺的擺動過程中，復擺會受到重力和轉軸反作用力的作用［1-3］，復擺結構示意圖如圖1所示。

如復擺剛體的質量為m，復擺繞其轉軸的轉動慣量為J，重心O點至質心C點的距離是l，那么周期的計算公式為

為了便于裝夾被測彈藥，復擺結構設計樣式較多［4］。復擺的研制原則是采用輕重量小質量的結構，對轉軸的轉動慣量要盡可能的小［5，6］，常見的復擺測試系統結構如圖2所示。

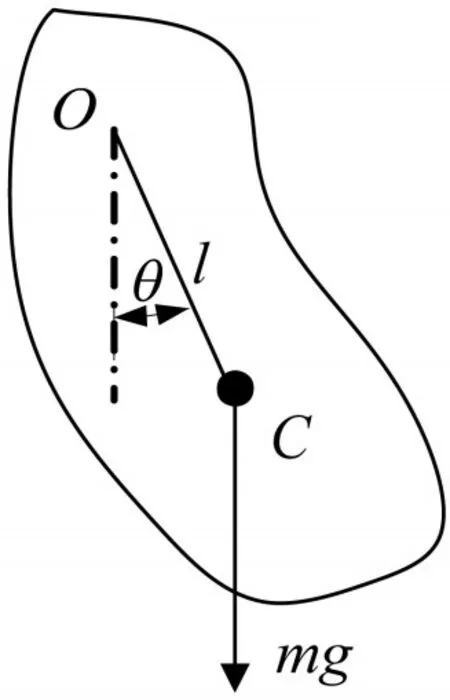
圖1 復擺結構示意圖

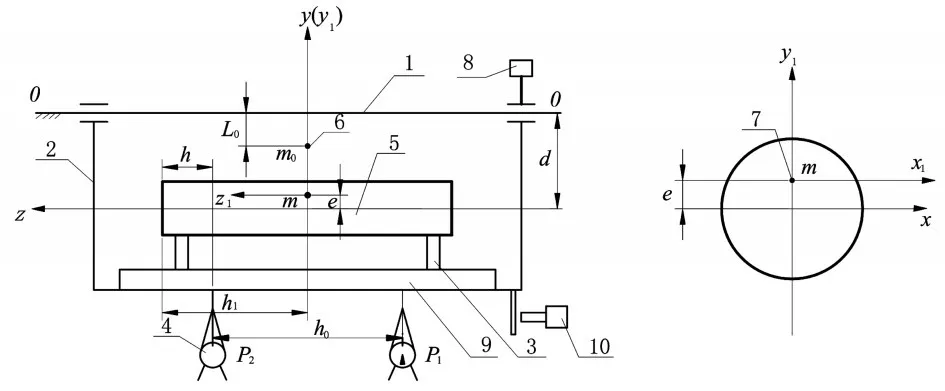
圖2 測試系統結構示意圖

測試系統工作時，需要把被測彈藥放在V槽上，用稱重傳感器獲得被測彈藥的重量（P=P1+P2），再測出其一端與質點的距離h，通過方程得出彈藥的軸向質心［7，8］。通過角度測量儀測得的偏角，來調整質心的位置，然后調整系統，使m1和m0在同一個橫軸面并將其固定，進行擺動周期的測量得到T1，再將彈體繞z軸旋轉180°，得到周期T2。

測試系統進行測試時，測量架繞O點擺動，質心C與轉軸之間的距離為l0，測量架繞O點擺動時的轉動慣量為J0。測量架繞轉軸轉動的擺振方程為：

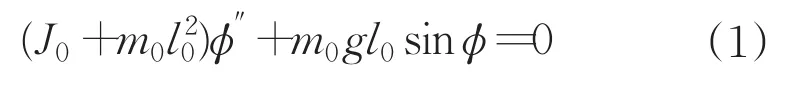
當測量架以較小角度擺動時(φ≤5°),方程（1）可簡化為：

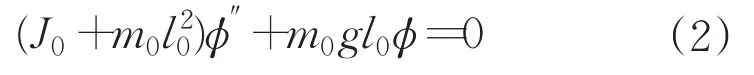
測量架的周期為：

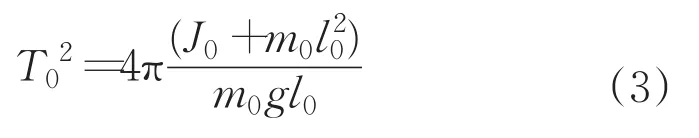
測量架的擺動方程為：

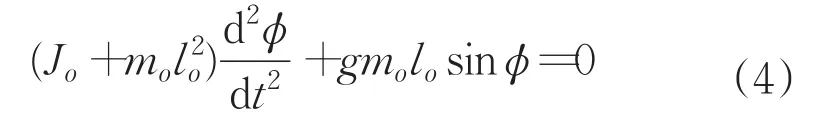
方程（4）可簡化為：

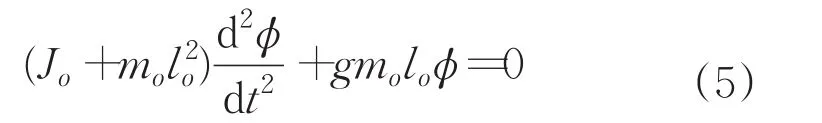
由此可獲得測量架的擺動周期（空盤周期）為：

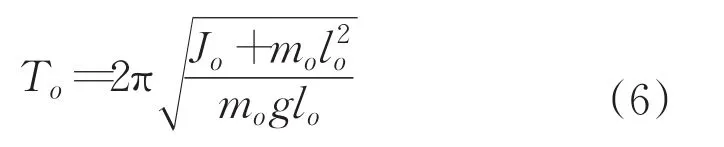
根據方程（6），可利用標準樣柱標定的方法來確定lo和Jo。標準樣柱的質量為ms，其轉動慣量為Js。測定標準樣柱的復擺擺動周期，可得：

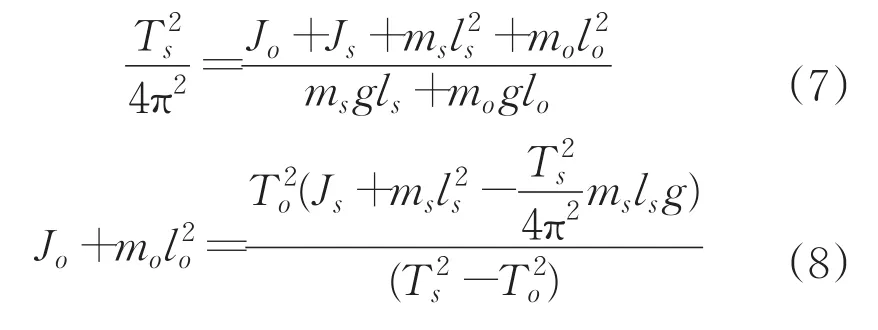
從方程（7）和（8）可知，需對復擺自身參數及m0進行測定，只有測定復擺的自身參數后，才能對彈藥的自身參數進行測試。為了消除彈藥測量結果受復擺自身參數誤差的影響，在對復擺自身參數進行測量時，其精度一般會高于正常測量彈藥精度的一個數量級。完成復擺自身參數的測量后，利用稱重傳感器和角度測量儀調整彈藥質心的位置，使彈藥位于yoz平面區間內，保持質心平面不動，再將彈藥繞y軸旋轉90°，測試系統結構示意圖如圖3所示。

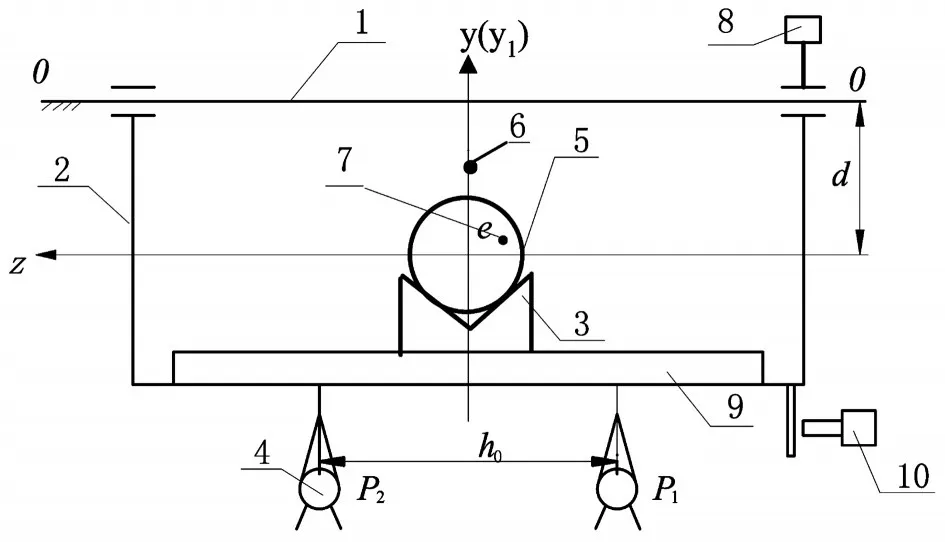
圖3 測試系統結構示意圖

2 測試精度分析

為提高測試系統的測試精度，需先測出旋轉軸線與彈藥軸線間距d，并調整質心位置，測試得到e值，在較小擺角情況下，系統的擺振方程為：

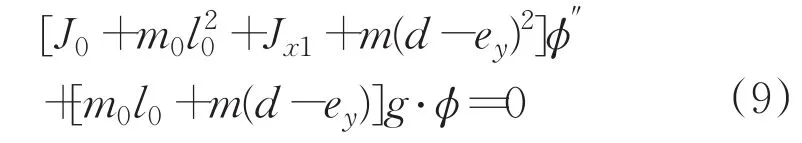
式中，ex=ecosθ,ey=esinθ；其中，θ為彈藥的初始角度，θ角是任意擺放確定的，也就是說，彈藥放在測量架上后進行測試時，不需要對彈藥的初始角度進行調整。

初始時刻彈藥和測量架的擺動周期T1為：

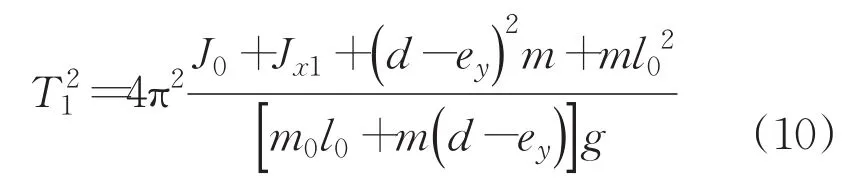
接下來，將彈藥繞其轉軸順時針旋轉180°，測得此時擺動周期T3為：

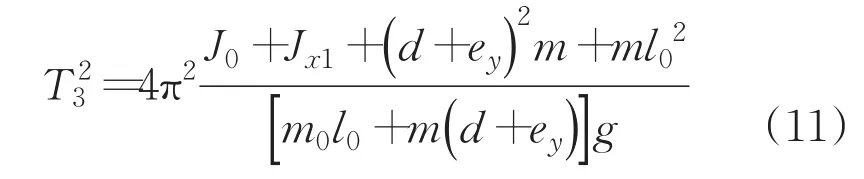
再將彈藥繞其轉軸逆時針回轉90°，測得此時擺動周期T2為：

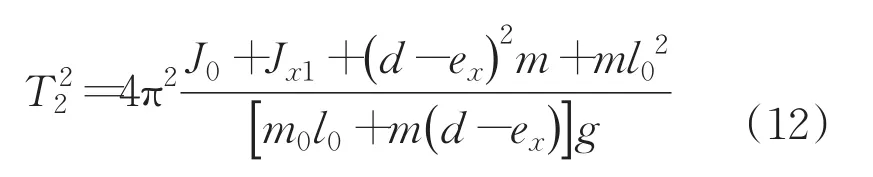
最后，再將彈藥繞其轉軸順時針轉180°后，測得此時擺動周期T4為：

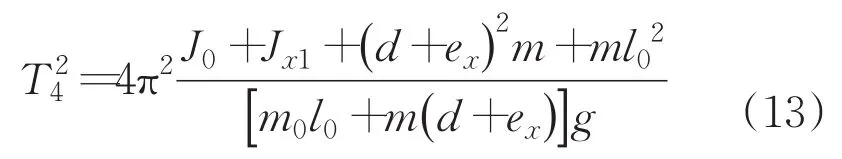
聯立上述方程得到質偏的方程：

對質偏進行精度分析，得到其精度的計算方程為：

假設在測量過程中的絕對誤差都相同，則有：

根據上述相關計算，可以知道測試系統具有以下不足之處：

（1）系統中含有參數d，在進行質偏的測試時要對其距離進行測試，會使系統誤差增加，從而會對整體的測試精度產生一定的影響；

（2）質偏計算方程過于復雜，容易出現計算錯誤，從而使測試結果出現誤差。

在原有系統結構的基礎上對其進行改進，優化相應機械結構，使得設備的旋轉軸線與彈藥的幾何軸線相重合，即d=0，從而方程（10）-方程（14）可以轉化為：

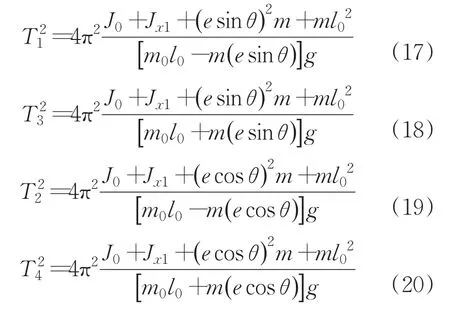
聯立上面的方程（17）、（18）、（19）、（20）可以得到：

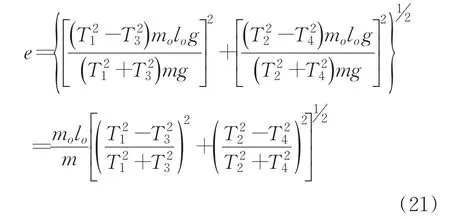
對方程（21）進一步簡化，質偏精度的計算方程為：

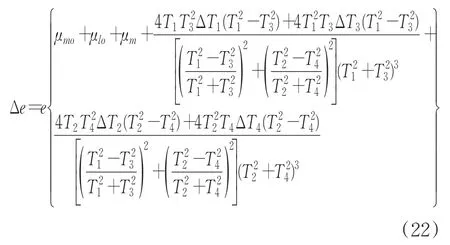
當ΔT1=ΔT2=ΔT3=ΔT4=ΔT，則有：

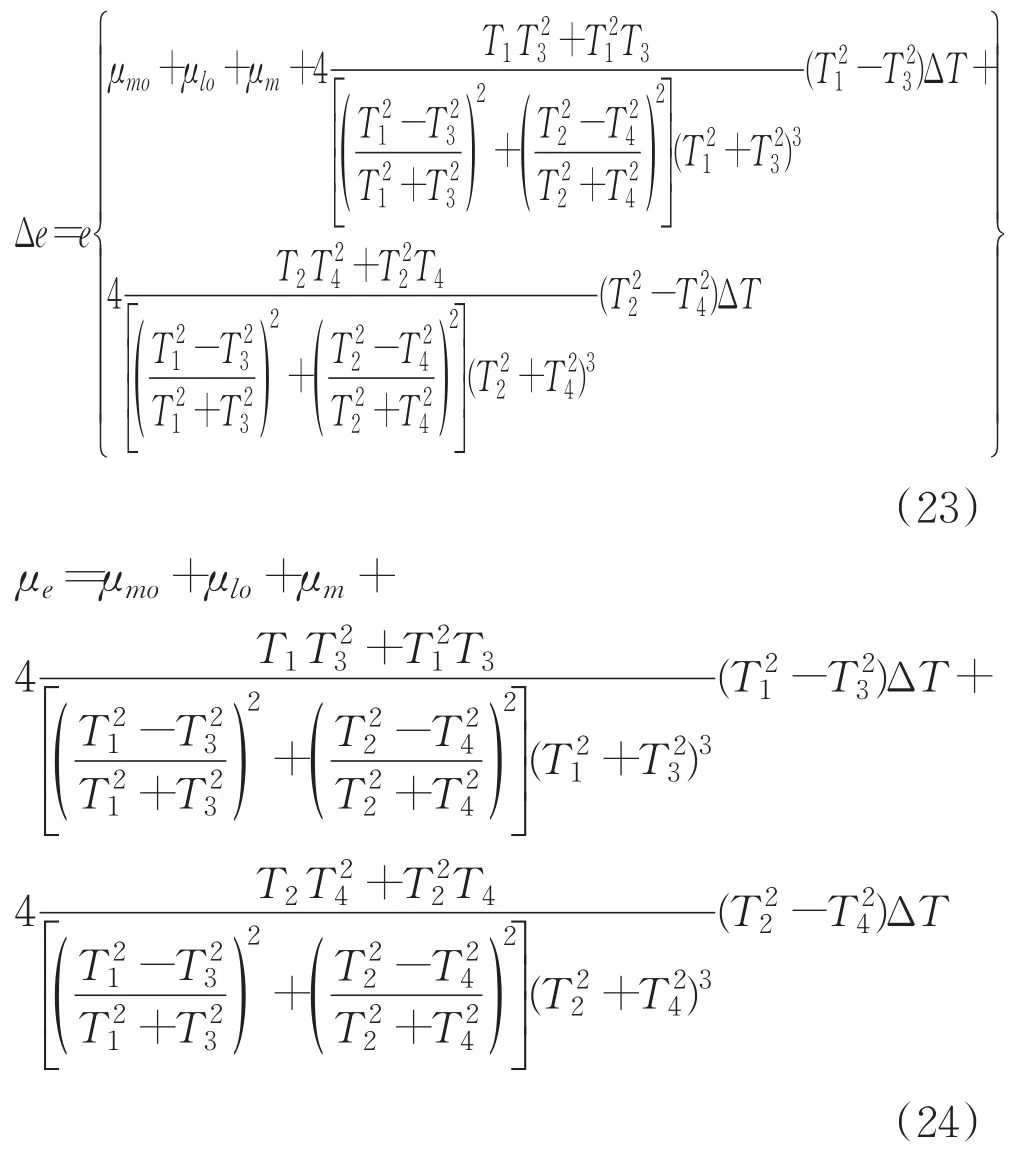
3 測試試驗

試驗采用鋼制圓柱回轉體代替彈藥，為了產生偏心，在圓柱試件外表面沿其端部加工出一個半徑為4mm的小圓柱槽，試驗用試件尺寸示意圖如圖4所示。

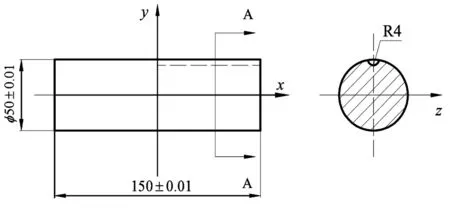
圖4 試件尺寸示意圖

經過測試，可知試件的參數如下：

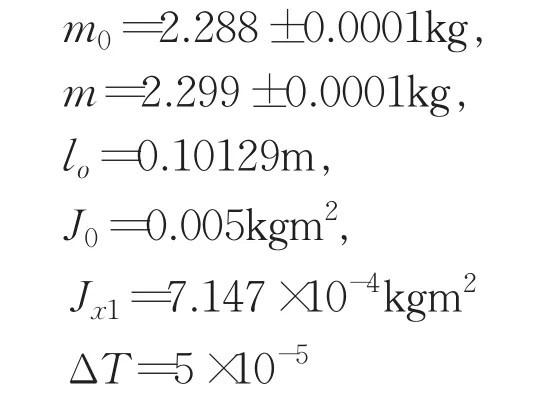
在進行系統周期測試過程中，取其中5個周期的平均值來計算系統質偏，測得周期值如表1所示。

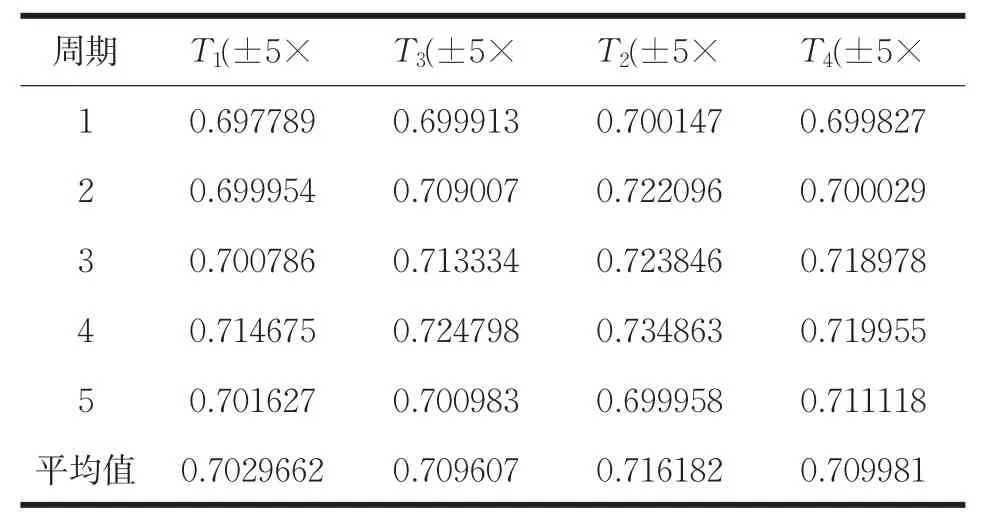
表1 測試系統周期值

由此得到四組周期的平均值，以此平均值來計算系統誤差。

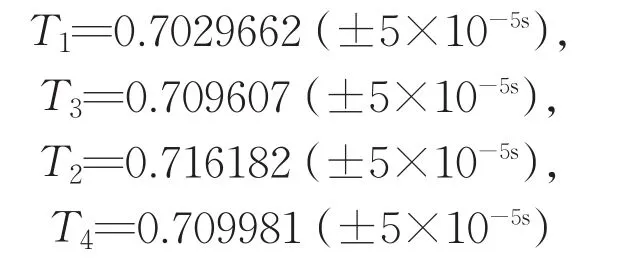
通過計算獲得了相應的測試系統誤差值，測試系統誤差值如表2所示。

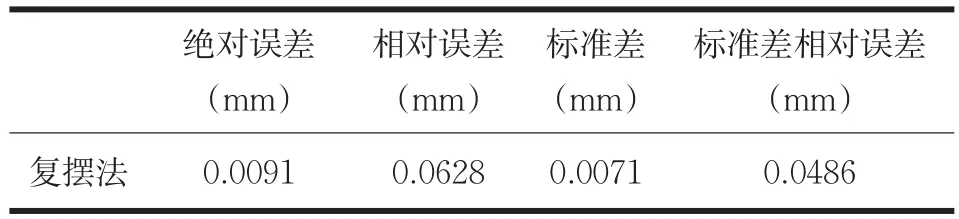
表2 測試系統誤差值

通過實際測試的試驗值與理論計算值的對比分析，可得到表3的測試結果。

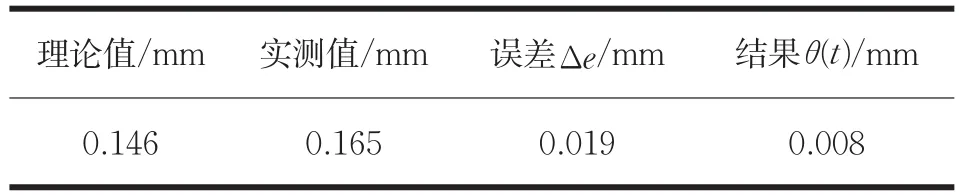
表3 測試結果

實測值與理論值的對比分析可知，用復擺法測量彈藥質偏是可行的。

4 結語

根據復擺測試原理及測試結構進行系統誤差分析和計算，獲得彈藥質偏的測試精度。要測得彈藥的質偏參數，需對彈藥的質心位置進行測試。彈藥的質心對彈藥飛行時的運行軌跡、空間姿態和命中率都有著重大的影響。

通過對質偏測試儀器的改進，使測試儀器在設計及制造過程簡單可靠，提高了質偏測試精度和測試效率并減少研制成本，取得了良好的測試效果。

［1］車英，李占國，陳禮華等.彈丸轉動慣量測試系統及其誤差分析［J］.兵工學報，2000，21（1）：87-89.

［2］Hou W，Zheng B，Yang RF.A measuring method on moment of inertia of largescale ammunition［J］.Journal of China Ordnance Society，2005（1）：41-46.

［3］張曉琳，張烈山，姜廣利，等.基于復合扭擺運動的飛行器轉動慣量測量方法研究［J］.航天制造技術，2011，12（6）：19-22.

［4］馮艷秋.轉動慣量測試系統設計及精度分析［D］.長春：長春理工大學，2009.

［5］張心明，馮艷秋，倪坤.箭彈質偏與轉動慣量測量裝置的優化設計［J］.現代制造工程，2012（11）：87-90.

［6］于治會.粗短棒偏心位置的測定方法［J］.宇航計測技術，1991（04）：46-51.

［7］鄭賓，侯文，楊瑞峰.大尺寸柱狀結構質量、質心測量方法［J］.測試技術學報，2002，16（2）：108-111.

［8］顧強，李波.彈體質量、質心及質偏的新三點測量法［J］.彈箭與制導學報，2005，25（S9）：177-178.

Ammunition Centroidal Deviation Measuring and Precision Analyzing Based on Compound Pendulum

LIU Yongfu1，ZHANG Xinming2，LI Junye2，WANG Demin2，YIN Yanlu2
（1.NO.63867 Branch of People’s Liberation Army，Baicheng，137000；2.School of Mechatronic Engineering，Changchun University of Science and Technology，Changchun 130022）

The ammunition is an important part of weapon equipment system，where the position of the center of mass affects speed and stability of the ammunition；Eccentric position determines orbit of the rocket，and it directly affects the rocket target shooting.These parameters is of great significance.In this paper，based on the original compound pendulum theory and structure，further research is conducted，which makes the tedious calculation formula simplified，and is convenient for measurement and calculation.The research provides theoretical basis for compound pendulum measuring method of mass eccentricity.

compound pendulum method；measurement；test error；precision analysis

TG484

A

1672-9870（2017）04-0053-05

2017-01-16

中國人民解放軍總裝備部項目

劉永付（1974-），男，工程師，E-mail：1847515933@qq.com